La Fig. 17.2.6A muestra una distribución de frecuencia que es el resultado de sobreponer las distribuciones normales "a" y "b". Se supone que las frecuencias de tallas de la Fig. 17.2.6B igualmente corresponden a una combinación de dos distribuciones normales. El objetivo del ejercicio es separar estas dos componentes. El tamaño de la muestra es 398. Suponga que cada una de estas componentes incluye el 50% de los ejemplares, es decir 199. Así también, suponga que las frecuencias del lado izquierdo, algo más abajo del tope, son totalmente representativas de la componente "a", mientras que las frecuencias a la derecha del valor máximo representan adecuadamente a la componente "b".
Fig. 17.2.6A Distribución combinada en que se superponen dos distribuciones normales.
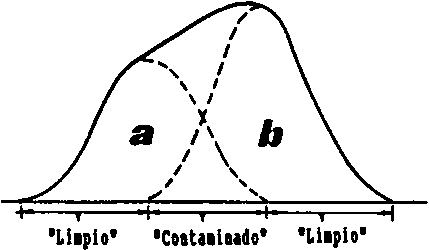
Fig. 17.2.6B Distribución de frecuencias de la muestra (se supone que éstas están constituidas por dos distribuciones normales).
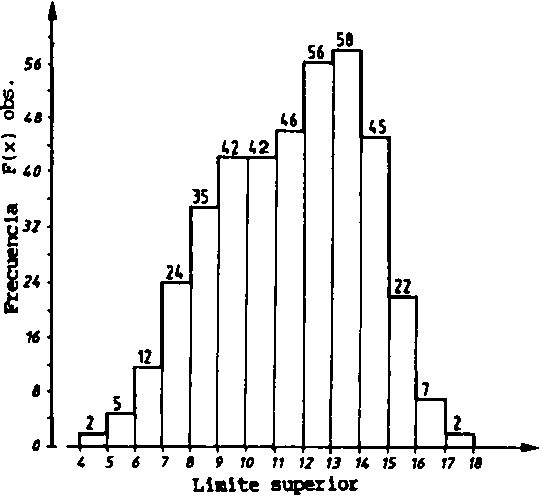
Tareas:
1) Complete la hoja de trabajo 2.6a.2) Dibuje D ln F(z) = y' contra x + dL/2 = z y decida qué puntos caen en una línea recta, con pendiente negativa (ver Fig. 2.6.5).
3) Seleccione los puntos que utilizará para el análisis de regresión lineal. Evite el área de sobreposición y aquellos puntos basados en muy pocas observaciones. Calcule las dos regresiones lineales, determinando a y b para cada una de ellas.
4) Calcule para cada componente
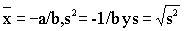
5) Dibuje las dos líneas que representan cada una de las distribuciones.
6) Seguidamente se desea convertir las líneas rectas en las correspondientes distribuciones normales teóricas (calculadas). Utilizando la Ec. 2.2.1 calcule Fc(x) para las dos distribuciones normales en un número suficiente de valores - x, de manera que le permita trazar las curvas en forma de campana que se muestran sobrepuestas en la Fig. 17.2.6B. Suponga n = 199 para cada componente. (Utilice el mismo método presentado en el Ejercicio 2.2). Complete la hoja de trabajo 2.6b.
Hoja de trabajo 2.6a
|
intervalo |
x |
F(x) |
ln F(x) |
D ln F(z) |
z = x + dL/2 |
|
4 - 5 |
4.5 |
2 |
0.693 |
0.916 |
5 |
|
5 - 6 |
5.5 |
5 |
1.609 |
0.875 |
6 |
|
6 - 7 |
6.5 |
12 |
|
|
7 |
|
7 - 8 |
7.5 |
24 |
|
|
|
|
8 - 9 |
8.5 |
35 |
|
|
|
|
9 - 10 |
9.5 |
42 |
|
|
|
|
10 - 11 |
10.5 |
42 |
|
|
|
|
11 - 12 |
11.5 |
46 |
|
|
|
|
12 - 13 |
12.5 |
56 |
|
|
|
|
13 - 14 |
13.5 |
58 |
|
|
|
|
14 - 15 |
14.5 |
45 |
|
|
|
|
15 - 16 |
15.5 |
22 |
3.091 |
-1.145 |
16 |
|
16 - 17 |
16.5 |
7 |
1.946 |
-1.253 |
17 |
|
17 - 18 |
17.5 |
2 |
0.693 |
|
|
Hoja de trabajo 2.6b
|
Primera componente |
Segunda componente | ||||
|
A= __________ |
A= __________ | ||||
|
B= |
B= | ||||
|
C= |
C= | ||||
|
Fc(x) =A * exp [B * (x- | |||||
|
x |
Fc (x) primera |
Fc (x) segunda |
x |
Fc (x) primera |
Fc (x) segunda |
|
1.5 |
|
|
11.5 |
|
|
|
2.5 |
|
|
12.5 |
|
|
|
3.5 |
|
|
13.5 |
|
|
|
4.5 |
|
|
14.5 |
|
|
|
5.5 |
|
|
15.5 |
|
|
|
6.5 |
|
|
16.5 |
|
|
|
7.5 |
|
|
17.5 |
|
|
|
8.5 |
|
|
18.5 |
|
|
|
9.5 |
|
|
19.5 |
|
|
|
10.5 |
|
|
20.5 |
|
|