Ejercicio 3.1 La ecuación de crecimiento de von Bertalanffy

Hoja de trabajo 3.1

edad años	talla estándar cm	talla total cm	peso del cuerpo g
0.5	1.0	1.4	0.04
1.0	6.6	8.0	9
1.5	11.8	14.1	45
2	16.5	19.7	118
3	24.9	29.6	380
4	32.0	37.9	775
5	38.0	45.0	1262
6	43.0	51.0	1802
7	47.3	56.0	2359
8	50.9	60.3	2909
9	54.0	63.9	3434
10	56.6	67.0	3922
12	60.6	71.7	4770
14	63.5	75.1	5444
16	65.5	77.5	5961
20	68.1	80.5	6637
50	70.7	83.6	7388

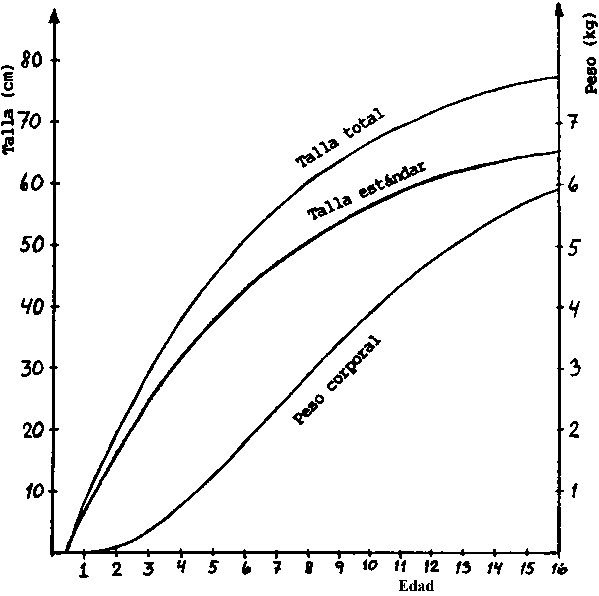
Fig. 18.3.1 Curvas de crecimiento basado en las ecuaciones de crecimiento de von Bertalanffy (ver hoja de trabajo 3.1).

Ejercicio 3.1.2 La ecuación de von Bertalanffy basada en el peso

Hoja de trabajo 3.1.2

t	L(t)	w(t)	t	L(t)	w(t)
0	2.54	0.38	0.9	9.34	19.00
0.1	3.63	1.11	1.0	9.78	21.83
0.2	4.62	2.29	1.2	10.55	27.36
0.3	5.51	3.90	1.4	11.17	32.53
0.4	6.32	5.88	1.6	11.69	37.21
0.5	7.05	8.16	1.8	12.11	41.37
0.6	7.71	10.69	2.0	12.45	44.99
0.7	8.31	13.37	2.5	13.06	51.93
0.8	8.85	16.16	3.0	13.43	56.47

Fig. 18.3.1.2 Curvas de crecimiento para el motambo esplendor, basado en las ecuaciones de crecimiento de von Bertalanffy para la talla y el peso (ver hoja de trabajo 3.1.2).

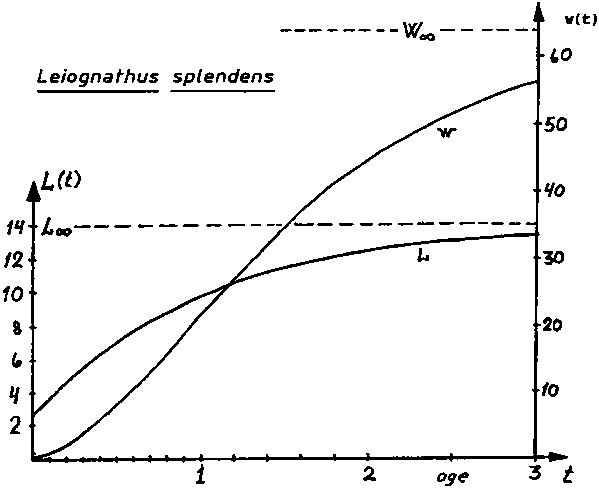
Fuente de la información: Pauly (1980).

Ejercicio 3.2.1 Datos de lecturas de edad y composición de tallas (clave edad/talla)

Hoja de trabajo 3.2.1

Ejercicio 3.3.1 El gráfico de Gulland y Holt

Hoja de trabajo 3.3.1

A	B	C	D	E	F
pez	L(t)	L(t+D t)	D t
no.	cm	cm	días	cm/año (y)	cm (x)
1	9.7	10.2	53	3.44	9.95
2	10.5	10.9	33	4.42	10.70
3	10.9	11.8	108	3.04	11.35
4	11.1	12.0	102	3.22	11.55
5	12.4	15.5	272	4.16	13.95
6	12.8	13.6	48	6.08	13.20
7	14.0	14.3	53	2.07	14.15
8	16.1	16.4	73	1.50	16.25
9	16.3	16.5	63	1.16	16.40
10	17.0	17.2	106	0.69	17.10
11	17.7	18.0	111	0.99	17.85

a (intercepto) = 8.77	b (pendiente) = -0.431
K= -b = 0.43 por año	L¥ = -a/b = 20.3 cm
sb = 0.145	t9 = 2.26
Intervalo de confianza para K = [0.10, 0.76]

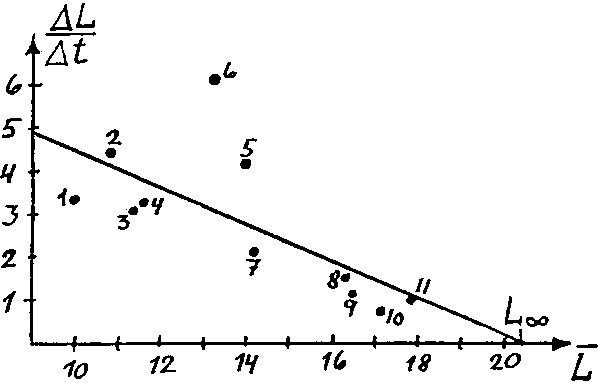
Fig. 18.3.3.1 Gráfico de Gulland y Holt (ver hoja de trabajo 3.3.1).

Ejercicio 3.3.2 El gráfico de Ford-Walford y el método de Chapman

Hoja de trabajo 3.3.2

método	Ford-Walford		Chapman
t	L(t + D t) (y)	L(t) (x)	L(t + D t) - L(t) (y)
1	55	35	20
2	75	55	20
3	90	75	15
4	105	90	15
5	115	105	10
a (intercepto)	26.2		26.2
b (pendiente)	0.86		- 0.14
	0.0009268		0.0009271
sb =	0.030		0.030
tn-2 = t3 =	3.18		3.18
límites de confianza de b:	[0.76, 0.96]		[- 0.24, - 0.04]
K	- ln b/D t = 0.15		- (1/1) * ln (1 + b) =0.15
L¥	a/(1-b)=185 cm		- a/b = 185 cm

Fig. 18.3.3.2 Gráficos de Ford-Walford para el rabil, frente a las costas de Senegal (ver hoja de trabajo 3.3.2).

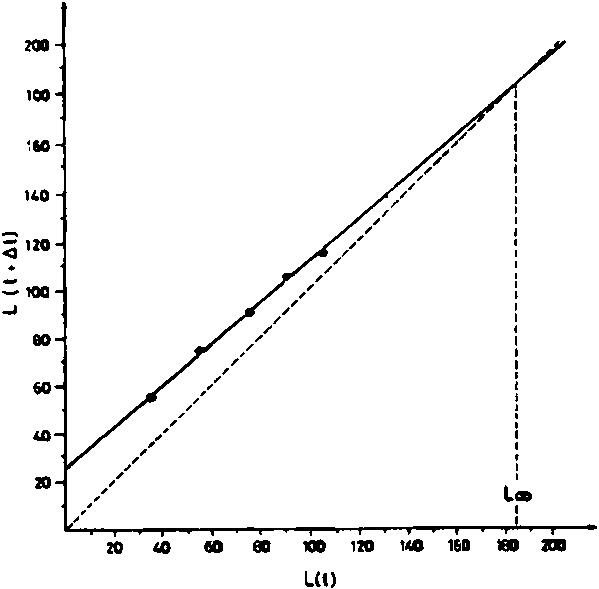
Fig. 18.3.3.2 Gráficos de Chapman para el rabil, frente a las costas de Senegal (ver hoja de trabajo 3.3.2).

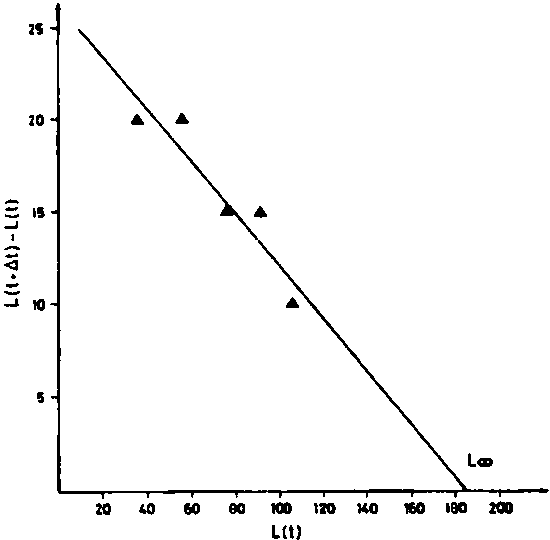
Fuente de la información: Postel (1955).

Ejercicio 3.3.3 El gráfico de von Bertalanffy

Se escoge 11 pulgadas como estimado para L_¥ . (Muy pocos, 1.5% de los ejemplares son más largos que 11 pulgadas).

Se asigna arbitrariamente las edades 1, 2, 3 y 4 años a los cuatro grupos de edad

edad	L	- ln (1 - L/L¥ )
1	3.22	0.35
2	5.33	0.66
3	7.62	1.18
4	9.74	2.17

b (pendiente) = K = 0.60 por año

Al menos, K tiene ahora el signo correcto.

sb² = 0.00119, sb = 0.109, t₂ = 4.3

Intervalo de confianza de K: [0.13, 1.07]

t_o no puede ser estimado porque no se conoce la edad absoluta.

Fig. 18.3.3.3 Gráficos de von Bertalanffy para Chrysophrys auratus.

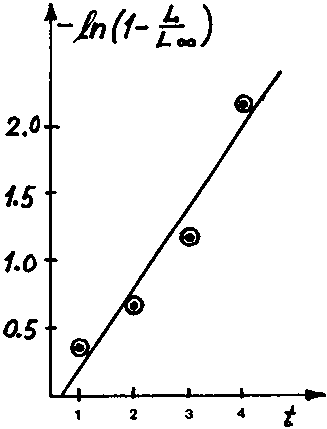
Fig. 18.3.3.3 Gráficos de Gulland y Holt para Chrysophrys auratus.

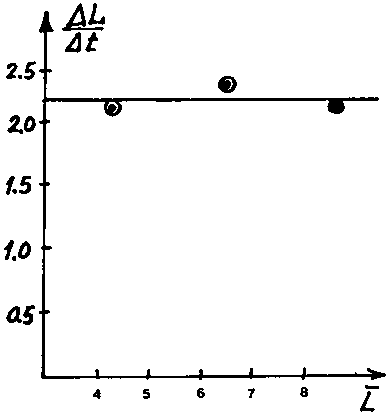
Fuente de la información: Cassie (1954).

Ejercicio 3.4.1 Método de Bhattacharya

No hay una solución "correcta" para este ejercicio. La siguiente es una "sugerencia de solución". No es el mismo resultado obtenido por Weber y Jothy (1977) utilizando el método de Cassie.

Fig. 18.3.4.1A Gráfico de Bhattacharya para la baga de dos hebras (ver hojas de trabajo 3.4.1a, b y c). Fuente de la información: Weber y Jothy (1977).

Hoja de trabajo 3.4.1a

Hoja de trabajo 3.4.1b

Hoja de trabajo 3.4.1c

Hoja de trabajo 3.4.1d

A	B	C	D	E	F	G	H	I
intervalo	N4+	ln N4+	D ln N4+	L	D ln N4	ln N4	N4	N5+
...............
20.75 - 21.75	20.2	3.006	-	20.75	?	muy pocas observaciones
21.75 - 22.75	44.4	3.793	0.787	21.75	?
22.75 - 23.75	15.5	2.741	- 1.052	22.75	?
23.75 - 24.75	6.5	1.892	- 0.869	23.75	?
24.75 - 25.75	2.6	0.956	- 0.916	24.75	?
25.75 - 26.75	1	0	- 0.956	25.75	?

Gráfico de Gulland y Holt:

edad	(Ni)	D L/D t
1	8.1
		6.1	11.15
2	14.2
		3.3	15.85
3	17.5

a (intercepto) = 12.7	b (pendiente) =-0.60
K = - b = 0.60 por año	L¥ = -a/b =21.4 cm

Fig. 18.3.4.1B Gráfico de Gulland y Holt en el que se utilizan las longitudes medias de las cohortes obtenidas al utilizar el método de Battacharya (ver hojas de trabajo 3.4.1a, b, c y figura 18.3.4.1A).

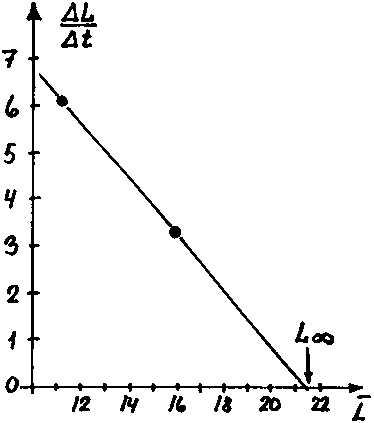
Ejercicio 3.4.2 Análisis de progresión modal

A. Leiognathus splendens:

Hoja de trabajo 3.4.2

Gráfico de:	Gulland y Holt			Von Bertalanffy
fecha de muestreo	L(t)	D L/D t		t	- ln(1-L/L¥ )
1 Junio	2.8			0.42	0.325
		6.8	3.65
1 Septiembre	4.5			0.67	0.590
		5.2	5.15
1 Diciembre	5.8			0.92	0.854
		4.0	6.30
1 Marzo	6.8			1.17	1.119
a (intercepto)	10.65			- 0.12
b (pendiente, - K)	- 1.06			1.06
- a/b	L¥ =10.1			to = 0.11

L(t) = 10.1 * [1 - exp(-1.1 * (t-0.11))]

Fig. 18.3.4.2A Progresión de las modas en las distribuciones de frecuencias de talla mensuales del motambo esplendor (ver hoja de trabajo 3.4.2).

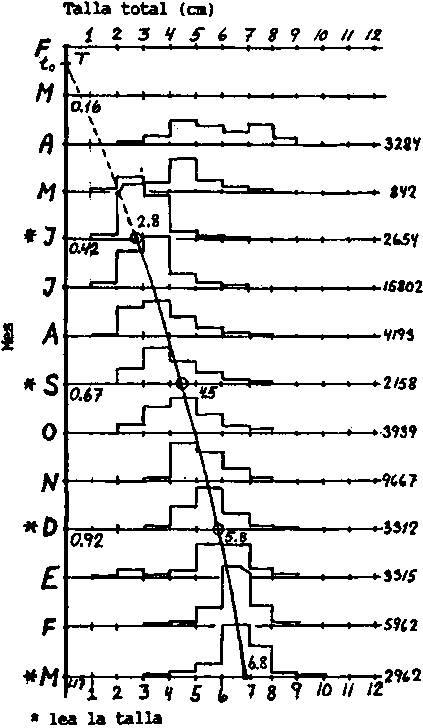
Fuente de la información: Tiews y Caces-Borja (1965).

B. Rastrelliger kanagurta:

Gráfico de:	Gulland y Holt			Von Bertalanffy
fecha de muestreo	L(t)	D L/D t		t	- ln (1-L/L¥ )
1 Febrero	13.3			0.08	0.648
		21.6	14.20
1 Marzo	15.1			0.17	0.779
		17.4	16.55
1 Mayo	18.0			0.33	1.036
		16.8	18.70
1 Junio	19.4			0.42	1.189
		13.2	19.95
1 Julio	20.5			0.50	1.327
		9.6	20.9
1 Agosto	21.3			0.58	1.442
a (intercepto)	44.57			0.512
b (pendiente, K)	- 1.60			1.61
-a/b	L¥ = 27.9			to = - 0.32

L(t) = 27.9 * [1 - exp(-1.6 * (t + 0.32))]

Fig. 18.3.4.2B Progresión de las modas en las distribuciones de frecuencias de talla de la caballa de la India (ver hoja de trabajo 3.4.2).

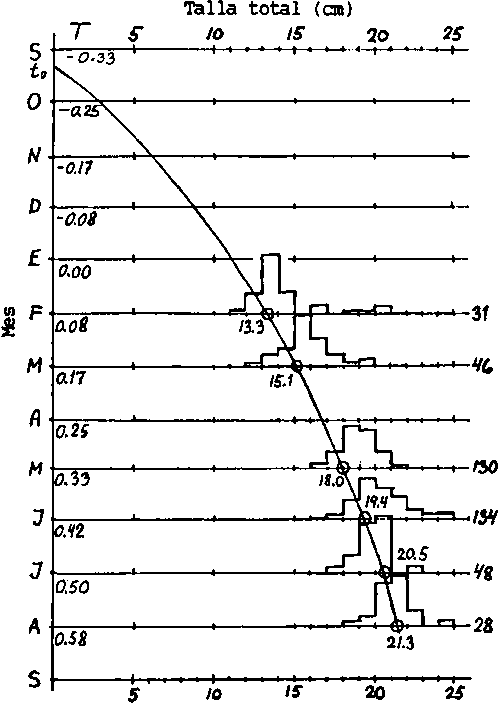
Fuente de la información: BFAR, Manila (1965).

Ejercicio 3.5.1 ELEFAN I

Hoja de trabajo 3.5.1

Fig. 18.3.5.1 Información reestructurada y valores positivos más altos obtenidos con el ELEFAN I (ver hoja de trabajo 3.5.1, paso 5).

Ejercido 3.5.1a ELEFAN I, continuación

Hoja de trabajo 3.5.1a

Fig. 18.3.5.1a Distribución de frecuencias de talla reagrupada de 523 lucios (intervalos de longitud de 4 cm) (A) y la información reestructurada con el ELEFAN I (B); los valores positivos más altos se relacionan con las tallas medias determinadas a través de la lectura de edad (flechas). Ver hoja de trabajo 3.5.1a y figura 17.3.5.1C.