Hoja de trabajo 4.3
|
|
|
cohorte |
1982 O |
1982 P |
1981 O |
1981 P |
1980 O |
|
cohorte |
edad t1 |
CPUE |
|
|
|
|
|
|
1983 P |
0.64 |
182 |
0.99 |
1.00 |
1.01 |
1.01 |
1.00 |
|
1982 O |
1.14 |
111 |
- |
1.03 |
1.02 |
1.02 |
1.00 |
|
1982 P |
1.64 |
67 |
- |
- |
1.03 |
1.03 |
1.00 |
|
1981 O |
2.14 |
40 |
- |
- |
- |
1.02 |
0.98 |
|
1981 P |
2.64 |
24 |
- |
- |
- |
- |
0.94 |
P = primavera O = otoño
Ejercicio 4.4.3 La curva de captura linearizada en base a los datos de composición de edades
Hoja de trabajo 4.4.3
|
edad |
año |
C(y, t, t+1) |
ln C (y, t, t + 1) |
Observaciones |
|
(x) |
(y) |
|||
|
0 |
1974 |
599 |
6.395 |
no usado en el análisis |
|
1 |
1975 |
860 |
6.757 |
|
|
2 |
1976 |
1071 |
6.976 |
|
|
3 |
1977 |
269 |
5.596 |
usado en el análisis |
|
4 |
1978 |
69 |
4.234 |
|
|
5 |
1979 |
25 |
3.219 |
|
|
6 |
1980 |
8 |
2.079 |
|
|
7 |
1981 |
- |
- |
|
|
pendiente: b = -1.16 |
sb2 = [(sy/sx)2 - b2]/(n-2) = 0.002330 |
|
sb = 0.0483 |
sb* tn-2 = 0.0483 * 4.30 = 0.21 Z = 1.16 ±0.21 |
Fig. 18.4.4.3 Curva de captura linearizada en base a datos de composición de edades (ver hoja de trabajo 4.4.3).
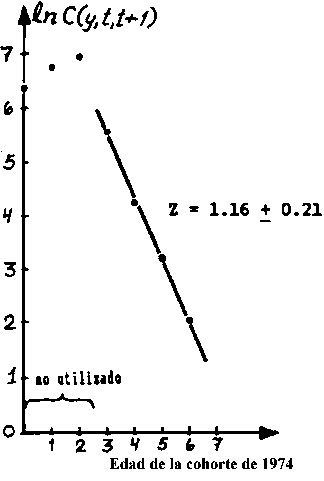
Ejercicio 4.4.5 La curva de captura linearizada basada en los datos de composición de talla
Hoja de trabajo 4.4.5
|
L1 - L2 |
C(L1,L2) |
t(L1) |
D t |
(x) |
(y) |
Z (pendiente) |
Observaciones |
|
7 - 8 |
11 |
0.452 |
0.0759 |
0.489 |
4.976 |
- |
no usado |
|
8 - 9 |
69 |
0.527 |
0.0796 |
0.567 |
6.765 |
- |
|
|
9 - 10 |
187 |
0.607 |
0.0836 |
0.648 |
7.712 |
- |
|
|
10 - 11 |
133 |
0.691 |
0.0881 |
0.734 |
7.319 |
- |
|
|
11 - 12 |
114 |
0.779 |
0.0931 |
0.825 |
7.110 |
- |
|
|
12 - 13 |
261 |
0.872 |
0.0987 |
0.&21 |
7.880 |
- |
|
|
13 - 14 |
386 |
0.971 |
0.1050 |
1.022 |
8.210 |
- |
|
|
14 - 15 |
445 |
1.076 |
0.112 |
1.13 |
8.286 |
- |
|
|
15 - 16 |
535 |
1.188 |
0.120 |
1.25 |
8.400 |
- |
usado en el análisis |
|
16 - 17 |
407 |
1.308 |
0.130 |
1.37 |
8.051 |
- |
|
|
17 - 18 |
428 |
1.438 |
0.141 |
1.51 |
8.019 |
1.43 |
|
|
18 - 19 |
338 |
1.579 |
0.154 |
1.65 |
7.693 |
1.60 |
|
|
19 - 20 |
184 |
1.733 |
0.170 |
1.82 |
6.987 |
2.27 |
|
|
20 - 21 |
73 |
1.903 |
0.190 |
2.00 |
5.953 |
3.07 |
|
|
21 - 22 |
37 |
2.092 |
0.214 |
2.20 |
5.152 |
3.45 |
|
|
22 - 23 |
21 |
2.307 |
0.246 |
2.43 |
4.446 |
3.54 |
|
|
23 - 24 |
19 |
2.553 |
0.290 |
2.69 |
4.183 |
3.30 |
|
|
24 - 25 |
8 |
2.843 |
0.352 |
3.01 |
3.124 |
3.20 |
|
|
25 - 26 |
7 |
3.195 |
0.448 |
3.40 |
2.749 |
- |
demasiado cerca de L¥ |
|
26 - 27 |
2 |
3.643 |
0.617 |
3.92 |
1.176 |
- |
Detalles de los análisis de regresión:
|
rango de talla |
pendiente |
número de observaciones |
distrib. Student |
varianza de la pendiente |
desviación estándar de la pendiente |
límites de confianza |
|
L1 - L2 |
Z |
n |
tn-2 |
sb2 |
sb |
Z ± tn-2 * sb |
|
15 - 16 |
- |
1 |
- |
- |
- |
- |
|
16 - 17 |
- |
2 |
- |
- |
- |
- |
|
17 - 18 |
1.43 |
3 |
12.70 |
0.59 |
0.7681 |
1.43 ± 9.75 |
|
18 - 19 |
1.60 |
4 |
4.30 |
0.12 |
0.3464 |
1.60 ± 1.49 |
|
19 - 20 |
2.27 |
5 |
3.18 |
0.156 |
0.3950 |
2.27 ± 1.26 |
|
20 - 21 |
3.07 |
6 |
2.78 |
0.228 |
0.4475 |
3.07 ± 1.33 |
|
21 - 22 |
3.45 |
7 |
2.57 |
0.140 |
0.3742 |
3.45 ± 0.96 |
|
22 - 23 |
3.54 |
8 |
2.45 |
0.071 |
0.2665 |
3.54 ± 0.65 |
|
23 - 24 |
3.30 |
9 |
2.37 |
0.051 |
0.2258 |
3.30 ± 0.54 |
|
24 - 25 |
3.20 |
10 |
2.31 |
0.030 |
0.1732 |
3.20 ± 0.40 |
Ejercicio 4.4.6 La curva de captura acumulada basada en los datos de composición de talla (el método de Jones y van Zalinge)
Hoja de trabajo 4.4.6
|
L1 - L2 |
C(L1,L2) |
S C(L1,L¥ ) acumulada |
ln S C(L1,L¥ ) |
In(L¥ -L1) |
pendiente |
Observaciones |
|
7 - 8 |
11 |
3665 |
8.207 |
3.100 |
- |
no usado |
|
8 - 9 |
69 |
3654 |
8.204 |
3.054 |
- |
|
|
9 - 10 |
187 |
3585 |
8.185 |
3.006 |
- |
|
|
10 - 11 |
133 |
3398 |
8.131 |
2.955 |
- |
|
|
11 - 12 |
114 |
3265 |
8.091 |
2.901 |
- |
|
|
12 - 13 |
261 |
3151 |
8.055 |
2.845 |
- |
|
|
13 - 14 |
386 |
2890 |
7.969 |
2.785 |
- |
|
|
14 - 15 |
445 |
2504 |
7.825 |
2.721 |
- |
|
|
15 - 16 |
535 |
2059 |
7.630 |
2.653 |
- |
usado en el análisis |
|
16 - 17 |
407 |
1524 |
7.329 |
2.580 |
- |
|
|
17 - 18 |
428 |
1117 |
7.018 |
2.501 |
4.03 |
|
|
18 - 19 |
338 |
689 |
6.535 |
2.416 |
4.56 |
|
|
19 - 20 |
184 |
351 |
5.861 |
2.322 |
5.28 |
|
|
20 - 21 |
73 |
167 |
5.118 |
2.219 |
5.81 |
|
|
21 - 22 |
37 |
94 |
4.543 |
2.104 |
5.86 |
|
|
22 - 23 |
21 |
57 |
4.043 |
1.974 |
5.62 |
|
|
23 - 24 |
19 |
36 |
3.584 |
1.825 |
5.25 |
|
|
24 - 25 |
8 |
17 |
2.833 |
1.649 |
5.00 |
|
|
25 - 26 |
7 |
9 |
2.197 |
1.435 |
- |
demasiado cerca de L¥ |
|
26 - 27 |
2 |
2 |
0.693 |
1.163 |
- |
Detalles de los análisis de regresión:
|
rango de talla |
pendiente *K |
número de obs. |
Distrib. Student |
varianza de la pendiente |
desviación estándar de la pendiente |
límites de confianza de Z |
|
L1 - L2 |
Z |
n |
tn-2 |
sb2 |
sb |
Z ± K * tn-2 * sb |
|
15 - 16 |
- |
1 |
- |
- |
- |
- |
|
16 - 17 |
- |
2 |
- |
- |
- |
- |
|
17 - 18 |
2.44 |
3 |
12.70 |
0.00289 |
0.05376 |
2.44 ± 0.41 |
|
18 - 19 |
2.77 |
4 |
4.30 |
0.0858 |
0.2929 |
2.77 ± 0.76 |
|
19 - 20 |
3.20 |
5 |
3.18 |
0.169 |
0.4111 |
3.20 ± 0.79 |
|
20 - 21 |
3.52 |
6 |
2.78 |
0.141 |
0.3755 |
3.52 ± 0.63 |
|
21 - 22 |
3.55 |
7 |
2.57 |
0.064 |
0.2530 |
3.55 ± 0.39 |
|
22 - 23 |
3.41 |
8 |
2.45 |
0.045 |
0.2121 |
3.41 ± 0.32 |
|
23 - 24 |
3.20 |
9 |
2.37 |
0.056 |
0.2366 |
3.20 ± 0.34 |
|
24 - 25 |
3.03 |
10 |
2.31 |
0.045 |
0.2121 |
3.03 ± 0.30 |
K = 0.607 por año
Ejercicio 4.4.6a El método de Jones y van Zalinge aplicado al camarón
Hoja de trabajo 4.4.6a
|
talla del caparazón (mm) |
número desembarcados por año (millones) |
números acumulados por año (millones) |
lnS C(L1,L¥ ) |
ln(L¥ -L1) |
Z/K |
Observaciones |
|
L1 - L2 |
C(L1,L2) |
S C(L1,L¥ ) |
||||
|
11.18 - 18.55 |
2.81 |
18.16 |
2.899 |
3.592 |
- |
no usado |
|
18.55 - 22.15 |
1.30 |
15.35 |
2.731 |
3.366 |
- |
|
|
22.15 - 25.27 |
2.96 |
14.05 |
2.643 |
3.233 |
- |
|
|
25.27 - 27.58 |
3.18 |
11.09 |
2.406 |
3.101 |
- |
usado en el análisis |
|
27.58 - 29.06 |
2.00 |
7.91 |
2.068 |
2.992 |
- |
|
|
29.06 - 30.87 |
1.89 |
5.91 |
1.777 |
2.915 |
3.36 |
|
|
30.87 - 33.16 |
1.78 |
4.02 |
1.391 |
2.811 |
3.52 |
|
|
33.16 - 36.19 |
0.98 |
2.24 |
0.806 |
2.663 |
3.68 |
|
|
36.19 - 40.50 |
0.63 |
1.26 |
0.231 |
2.426 |
3.32 |
|
|
40.50 - 47.50 |
0.63 |
0.63 |
- 0.462 |
1.946 |
muy cerca de L¥ |
|
Detalles de los análisis de regresión:
|
talla inferior |
pendiente |
número de obs. |
Distrib. Student |
varianza de la pendiente |
desv. estándar de la pendiente |
límites de confianza de Z/K |
|
L1 |
Z/K |
n |
tn-2 |
sb2 |
sb |
Z/K ± tn-2 * sb |
|
29.06 |
3.36 |
3 |
12.70 |
0.0354 |
0.1882 |
3.36 ± 2.39 |
|
30.87 |
3.52 |
4 |
4.30 |
0.0143 |
0.1196 |
3.52 ± 0.51 |
|
33.16 |
3.68 |
5 |
3.18 |
0.0096 |
0.0980 |
3.68 ± 0.31 |
|
36.19 |
3.32 |
6 |
2.78 |
0.0224 |
0.1497 |
3.32 ± 0.42 |
Fig. 18.4.4.6a Curva de captura acumulada basada en información de la pesquería industrial de camarón en Kuwait (ver hoja de trabajo 4.4.6a).
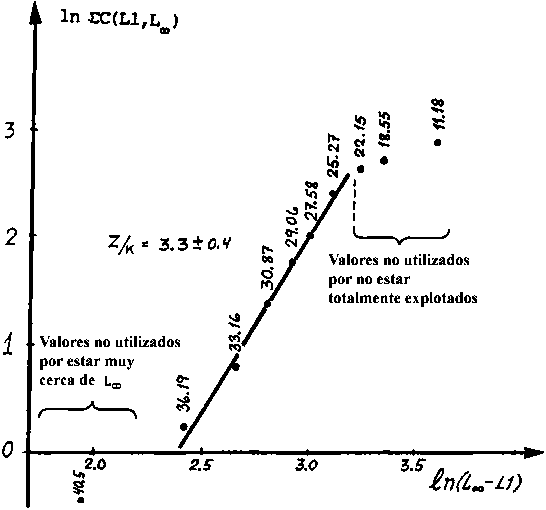
Fuente de la información: Jones y van Zalinge (1981).
Ejercicio 4.5.1 Ecuación Z de Beverton y Holt basada en los datos de talla (aplicada a camarones)
Fuente de la información: Munro (1983).
Ejercicio 4.5.4 El método de Powell-Wetherall aplicado a Haemulon sciurus
Hoja de trabajo 4.5.4
|
A |
B |
C |
D |
E |
F |
G |
H |
|
L' = L1 - L2 |
C(L1,L2) |
|
S C(L', ¥ ) |
|
|
|
|
|
14 - 15 |
1.8 |
14.5 |
100.1 |
26.10 |
2086.95 |
20.849 |
6.849 |
|
15 - 16 |
3.4 |
15.5 |
98.3 |
52.70 |
2060.85 |
20.965 |
5.965 |
|
16 - 17 |
5.8 |
16.5 |
94.9 |
95.70 |
2008.15 |
21.161 |
5.161 |
|
17 - 18 |
8.4 |
17.5 |
89.1 |
147.00 |
1912.45 |
21.464 |
4.464 |
|
18 - 19 |
9.1 |
18.5 |
80.7 |
168.35 |
1765.45 |
21.877 |
3.877 |
|
19 - 20 |
10.2 |
19.5 |
71.6 |
198.90 |
1597.1 |
22.306 |
3.306 |
|
20 - 21*) |
14.3 |
20.5 |
61.4 |
293.15 |
1398.2 |
22.772 |
2.772 |
|
21 - 22*) |
13.7 |
21.5 |
47.1 |
294.55 |
1105.1 |
23.463 |
2.463 |
|
22 - 23*) |
10.0 |
22.5 |
33.4 |
225.00 |
810.5 |
24.266 |
2.266 |
|
23 - 24*) |
6.3 |
23.5 |
23.4 |
148.05 |
585.5 |
25.021 |
2.021 |
|
24 - 25*) |
6.4 |
24.5 |
17.1 |
156.80 |
437.45 |
25.582 |
1.582 |
|
25 - 26*) |
5.3 |
25.5 |
10.7 |
135.15 |
280.65 |
26.229 |
1.229 |
|
26 - 27*) |
3.3 |
26.5 |
5.4 |
87.45 |
145.5 |
26.944 |
0.944 |
|
27 - 28*) |
1.8 |
27.5 |
2.1 |
49.50 |
58.05 |
27.643 |
0.643 |
|
28 - 29*) |
0.3 |
28.5 |
0.3 |
8.55 |
8.55 |
28.500 |
0.500 |
|
pendiente b = -0.2997 |
intercepto a = 8.795 |
* tallas consideradas como |
|
Z/K = -(1+b)/b = 2.337 |
L¥ = -a/b = 29.35 |
totalmente reclinadas (n = 9) |
|
Condiciones de equilibrio, con parámetros constantes. | ||
Comentarios:
En 1974, cuando Munro (1983) realizó el trabajo sobre Haemulon sciurus no era fácil estimar L¥ (el ELEFAN y otros procedimientos no estaban entonces disponibles). El gráfico de Ford-Walford resultó en líneas casi paralelas en todas las especies y, consecuentemente no permitía la estimación de valores confiables de L¥ . Basado en el análisis de la progresión de las modas, Munro obtuvo a través de prueba y error el valor de L¥ que parecía determinar una línea recta en el gráfico de von Bertalanffy. El resultado correspondió a un valor de L¥ = 40 cm, y a un valor de K = 0.26 por año. Al usar L' = 20 cm el autor obtuvo entonces un valor de Z/K = (40- 22.772)/2.772 = 6.2 de acuerdo a la fórmula de Beverton y Holt. (Este estimado representa una línea recta en el gráfico que conecta el punto L = 20 cm con el intercepto en el eje de las ordenadas de L¥ = 40 cm, equivalente a una línea con pendiente b = -(1 + Z/K)-1 = -0.14). De este modo, Munro obtuvo un valor Z = 6.2 * 0.26 = 1.6 por año. Sin embargo, en esta oportunidad se obtuvo un valor de L¥ » 30 cm, que modifica la estimación de Munro, pero que según el procedimiento que él empleó no se pueden rechazar los valores obtenidos de L¥ » 30 cm y K » 0.5 por año. Al utilizar nuestros resultados se obtiene un valor de Z = 2.34 * 0.5 = 1.17 por año.