In general, poverty maps do not measure casual linkages between variables. Hence, in order to describe these casual relationships, it is necessary to use an appropriate statistical analysis.
In particular, this study applies a spatial analysis to determine those variables that affect household poverty and to estimate the number of poor people in the target areas. This type of analysis is based on the assumption that measured geographic variables often exhibit properties of spatial dependency (the tendency of the same variables measured in locations in close proximity to be related) and spatial heterogeneity (non-stationarity of most geographic processes, meaning that global parameters do not well reflect processes occurring at a particular location). While traditional statistical techniques have treated these two last features as nuisances, spatial statistics considers them explicitly.
From the methodological point of view, the spatial analysis is based on five steps:
Step I. The spatial estimation of the impact of location characteristics of the areas in which the households reside is used to calculate the probability that these households are poor. The household data from the ECVand the community data from INFOPLAN are employed in order to determine the variables that best explain household consumption and poverty (Table 2).
Step II. Basic exploratory data analysis (EDA) techniques are applied and the spatial neighbourhood structure is defined in order to test the presence of spatial autocorrelation among the observed values.
Step III. The incidence of poverty in all the target areas (counties) in the country (Ecuador) is estimated on the basis of their location-specific characteristics (Table 3) and on the relationship estimated in Step I.
Step IV. The first validation of the estimation is executed comparing the incidence of poverty at the county level established by the spatial econometric estimation with the level of poverty in the county computed from the ECVsurvey data. This validation is based on the ranking of counties.
Step V. The second validation of the predictions is performed, aggregating the results at the province level and comparing this incidence of poverty with the Bigman et al. method and the Lanjouw et al. method.
In accordance with other similar studies, consumption is assumed to be the welfare indicator at the household level, and the headcount index is used as the measure of poverty.
Spatial autocorrelation is a property of spatial data that exists whenever there is a systematic pattern in the values recorded at locations in a map. In particular, where high values of a variable at one locality are associated with high values at neighbouring localities, the spatial autocorrelation is positive, and where high values correspond to low values in the adjacent localities, the spatial autocorrelation is negative.
In order to detect the spatial pattern (spatial association and spatial autocorrelation), some standard global and new local spatial statistics have been developed. These include Moran’s I, Geary’s C, G statistics (Getis, 1992), LISA (Anselin, 1995) and GLISA(Bao and Henry, 1996). All these spatial analytical techniques have two aspects in common. First, they start from the assumption of a spatially random distribution of data. Second, the spatial pattern, spatial structure, and form of spatial dependence are typically derived from the data (Bao, 1999).
| TABLE 2. Descriptive statistics on variables used in the estimation | |||||||||
|
Aggregation level |
Variable |
Type |
Urban |
Rural |
Data source |
||||
|
Mean |
Standard error |
No. observations |
Mean |
Standard error |
No. observations |
||||
|
Household |
Percentage adults illiterate in household |
Numeric |
0.09 |
0.18 |
3366 |
0.10 |
0.19 |
2264 |
ECV |
|
Household |
Percentage persons with diploma(1) |
Numeric |
0.06 |
0.16 |
3366 |
0.007 |
0.05 |
2264 |
ECV |
|
Household |
Adequate home |
Dummy |
0.93 |
0.25 |
3366 |
0.74 |
0.43 |
2264 |
ECV |
|
Household |
Home with drinking water |
Dummy |
0.79 |
0.40 |
3366 |
0.27 |
0.44 |
2264 |
ECV |
|
Household |
Home with adequate toilet |
Dummy |
0.94 |
0.23 |
3366 |
0.65 |
0.47 |
2264 |
ECV |
|
Household |
Home with adequate wall |
Dummy |
0.78 |
0.41 |
3366 |
0.40 |
0.49 |
2264 |
ECV |
|
Household |
Home with electricity public network |
Dummy |
0.97 |
0.16 |
3366 |
0.74 |
0.43 |
2264 |
ECV |
|
Household |
Waste: collection by truck |
Dummy |
0.76 |
0.42 |
3366 |
0.13 |
0.33 |
2264 |
ECV |
|
Household |
Persons per room |
Numeric |
1.83 |
1.37 |
3366 |
2.30 |
1.73 |
2 264 |
ECV |
|
County |
Population |
Numeric |
56 541.00 |
194 463.55 |
99 |
18 947.00 |
20 279.47 |
210 |
INFOPLAN |
|
County |
Mortality rate () |
Numeric |
47.01 |
11.31 |
99 |
66.42 |
14.81 |
210 |
INFOPLAN |
|
County |
Number of babies |
Numeric |
1 348 |
4 583.94 |
99 |
502 |
504.09 |
210 |
INFOPLAN |
|
County |
People < 5 km from road(3) |
Numeric |
32 267.62 |
99955.70 |
- |
32 267.62 |
99955.70 |
- |
FAO/SDRN GIS |
|
County |
People 5-15 km from road(3) |
Numeric |
5 542.75 |
14 347.99 |
- |
5 542.75 |
14 347.99 |
- |
FAO/SDRN GIS |
|
County |
People > 15 km from road(3) |
Numeric |
1 056.43 |
3 696.94 |
- |
1 056.43 |
3 696.94 |
- |
FAO/SDRN GIS |
|
County |
County area (km2) |
Numeric |
1 296.01 |
2 199.57 |
99 |
1 176.51 |
1 938.78 |
210 |
FAO/SDRN GIS |
|
County |
Cereal production coefficient |
Numeric |
205.20 |
416.94 |
99 |
140.30 |
302.30 |
210 |
FAO/SDRN GIS |
|
County |
Protected area |
Dummy |
0.26 |
0.44 |
99 |
0.28 |
0.45 |
210 |
FAO/SDRN GIS |
|
County |
> 35% irrigation area |
Dummy |
0.35 |
0.48 |
99 |
0.22 |
0.42 |
210 |
FAO/SDRN GIS |
|
County |
Closed forest |
Dummy |
0.29 |
0.46 |
99 |
0.33 |
0.47 |
210 |
FAO/SDRN GIS |
|
County |
Arable land(2) |
Factor |
- |
- |
99 |
- |
- |
210 |
FAO/SDRN GIS |
|
Province |
Erosion |
Factor |
- |
- |
21 |
- |
- |
21 |
INFOPLAN |
|
Province |
Climate |
Factor |
- |
- |
21 |
- |
- |
21 |
INFOPLAN |
|
Province |
Flooding area |
Dummy |
0.52 |
0.51 |
21 |
0.52 |
0.51 |
21 |
INFOPLAN |
|
Province |
Volcano area |
Dummy |
0.38 |
0.49 |
21 |
0.38 |
0.49 |
21 |
INFOPLAN |
(1) Secondary school.
(2) Arable land for each counties is obtained by first multiplying the weighted average area of the county by the percentage of arable land in the same county. The result is transformed as a factor which
takes a value of 0 if the number obtained is < 30%, 1 if between 30 and 60%, 2 if > 60%.(3) People < 5 km from road, People 515 km from road, People > 15 km from road are calculated on all the counties without distinction between urban and rural county.
| TABLE 3. Descriptive statistics on variables used in the prediction | |||||||||
|
Aggregation level |
Variable |
Type |
Urban |
Rural |
Data source |
||||
|
Mean |
Standard error |
No. observations |
Mean |
Standard error |
No. observations |
||||
|
County |
Percentage adults illiterate in county |
Numeric |
0.09 |
0.04 |
99 |
0.19 |
0.08 |
210 |
INFOPLAN |
|
County |
Percentage persons with diploma(1) |
Numeric |
0.13 |
0.06 |
99 |
0.04 |
0.02 |
210 |
INFOPLAN |
|
County |
Percentage of Adequate home |
Numeric |
0.91 |
0.06 |
99 |
0.69 |
0.19 |
210 |
INFOPLAN |
|
County |
Percentage of home with drinking water |
Numeric |
0.51 |
0.24 |
99 |
0.13 |
0.10 |
210 |
INFOPLAN |
|
County |
Percentage of home with adequate toilet |
Numeric |
0.63 |
0.12 |
99 |
0.20 |
0.12 |
210 |
INFOPLAN |
|
County |
Percentage of home with adequate wall |
Numeric |
0.66 |
0.15 |
99 |
0.29 |
0.20 |
210 |
INFOPLAN |
|
County |
Percentage of homes w. public electricity network |
Numeric |
0.91 |
0.05 |
99 |
0.48 |
0.22 |
210 |
INFOPLAN |
|
County |
W aste: collection by truck (%) |
Numeric |
0.63 |
0.20 |
99 |
0.09 |
0.11 |
210 |
INFOPLAN |
|
County |
Persons per room |
Numeric |
2.23 |
0.43 |
99 |
2.60 |
0.47 |
210 |
INFOPLAN |
|
County |
Population |
Numeric |
5 6541 |
194 463.55 |
99 |
1 8947 |
20 279.47 |
210 |
INFOPLAN |
|
County |
Mortality rate () |
Numeric |
47.01 |
11.31 |
99 |
66.42 |
14.81 |
210 |
INFOPLAN |
|
County |
Number of babies |
Numeric |
1 348 |
4 583.942 |
99 |
502 |
504.09 |
210 |
INFOPLAN |
|
County |
People < 5 km from road(3) |
Numeric |
32 267.62 |
99955.70 |
- |
32 267.62 |
99955.70 |
- |
FAO/SDRN GIS |
|
County |
People 5-15 km from road(3) |
Numeric |
5 542.75 |
14 347.99 |
- |
5 542.75 |
14 347.99 |
- |
FAO/SDRN GIS |
|
County |
People > 15 km from road(3) |
Numeric |
1 056.43 |
3 696.94 |
- |
1 056.43 |
3 696.94 |
- |
FAO/SDRN GIS |
|
County |
County area (km2) |
Numeric |
1 296.01 |
2 199.57 |
99 |
1 176.51 |
1 938.78 |
210 |
FAO/SDRN GIS |
|
County |
Cereal production coefficient |
Numeric |
205.20 |
416.94 |
99 |
140.30 |
302.30 |
210 |
FAO/SDRN GIS |
|
County |
Protected area |
Dummy |
0.26 |
0.44 |
99 |
0.28 |
0.45 |
210 |
FAO/SDRN GIS |
|
County |
> 35% irrigation area |
Dummy |
0.35 |
0.48 |
99 |
0.22 |
0.42 |
210 |
FAO/SDRN GIS |
|
County |
Closed forest |
Dummy |
0.29 |
0.46 |
99 |
0.33 |
0.47 |
210 |
FAO/SDRN GIS |
|
County |
Arable land(2) |
Factor |
- |
- |
99 |
- |
- |
210 |
FAO/SDRN GIS |
|
Province |
Erosion |
Factor |
- |
- |
21 |
- |
- |
21 |
INFOPLAN |
|
Province |
Climate |
Factor |
- |
- |
21 |
- |
- |
21 |
INFOPLAN |
|
Province |
Flooding area |
Dummy |
0.52 |
0.51 |
21 |
0.52 |
0.51 |
21 |
INFOPLAN |
|
Province |
Volcano area |
Dummy |
0.38 |
0.49 |
21 |
0.38 |
0.49 |
21 |
INFOPLAN |
(1) Secondary school.
(2) Arable land for each counties is obtained by first multiplying the weighted average area of the county by the percentage of arable land in the same county. The result is transformed as a factor which takes a value of 0 if the number obtained is < 30%, 1 if between 30 and 60%, 2 if > 60%.
(3) People < 5 km from road, People 515 km from road, People > 15 km from road are calculated on all the counties without distinction between urban and rural county.
The first measure of spatial autocorrelation was introduced by Moran (1950). The index is analogous to the conventional correlation coefficient, and its values range from 1 (strong positive spatial autocorrelation) to -1 (strong negative spatial autocorrelation). It is often used to measure the spatial autocorrelation of ordinal, interval or ratio data. Moran’s I is defined by:
|
|
(1) |
where
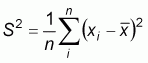 , xi
denotes the observed value of population at location
, xi
denotes the observed value of population at location
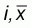 is the average of the
xi over the n locations, and wij is
the spatial weight measure of contiguity and is defined as 1 if location i
is contiguous to location j and 0 otherwise.
is the average of the
xi over the n locations, and wij is
the spatial weight measure of contiguity and is defined as 1 if location i
is contiguous to location j and 0 otherwise.
The choice of weights wij between neighbours is a crucial step in the analysis. There are many ways to assign neighbour weights, and the choice depends on the type of spatial application and on the research question. This specification requires a priori knowledge of the range and intensity of the spatial covariance between regions. Common methods include row standardization, length of common boundary and distance functions.
With regard to the weighting procedure, the use of generalized weighting matrix W, as opposed to a binary connection matrix, allows a set of weights to be chosen which are deemed appropriate from prior consideration. This matrix W offers great flexibility in defining the structure of the county system, and it permits items such as natural barriers and county size to be taken into account. It is important to note that the elements of W are non-stochastic and exogenous to the model. Typically, they are based on the geographic arrangement of the observations or contiguity. Weights are non-zero when two locations share a common boundary or are within a given distance of each other. However, this notation is general and alternative specifications of the spatial weights can be based on distance decay (inverse distance). In this study, the neighbourhood structure is based on inverse Euclidean distance (Anselin, 1992).
The expected value and variance of Moran’s I for a sample of size n could be calculated according to the assumed pattern of the spatial data distribution (Cliff and Ord, 1981).
For the assumption of a normal distribution:
|
|
(2) |
|
|
(3) |
For the assumption of random distribution:
|
|
(4) |
|
|
(5) |
where: 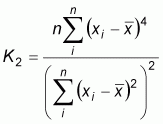 ,
, 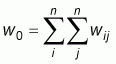 ,
,
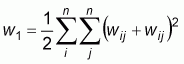 ,
, 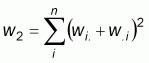 ,
wi. and w.i are the sum of the row i
and column i of the weight matrix respectively.
,
wi. and w.i are the sum of the row i
and column i of the weight matrix respectively.
The test of the null hypothesis that there is no spatial autocorrelation between observed values over the n locations can be conducted on the basis of the standardized statistics as follows:
|
|
(6) |
Moran’s I is significant and positive when the observed values of locations within a certain distance (d) tend to be similar, negative when they tend to be dissimilar, and approximately zero when the observed values are arranged randomly and independently over space.
Another index for testing the presence of spatial autocorrelation in the data is Geary’s C. It uses the sum of squared differences between pairs of data values as a measure of covariation. The formula of Geary’s C is:
|
|
(7) |
This index ranges between 0 and 2. Positive spatial autocorrelation is found with values ranging from 0 to 1 and negative spatial autocorrelation is found between 1 and 2.
For the assumption of a normal distribution:
|
|
(8) |
|
|
(9) |
For the assumption of random distribution:
|
|
(10) |
|
|
(11) |
The significance of Geary’s C is tested identically to that for Moran’s I.
The results of spatial autocorrelation tests should be used with caution. First, the choice of neighbours and their respective weights determines the values of Moran and Geary statistics. Anon-significant result indicates that there is no significant spatial autocorrelation given the neighbourhood structure provided. Second, a significant positive autocorrelation could be caused by a spatial pattern in the data not specified by the statistical model. The following section shows how this model misspecification can be controlled by incorporating a spatial weights matrix into the statistical model.
As a special case, generalized spatial linear models include spatial linear regression and analysis of variance models, spatial logit and probit models for binary responses, loglinear models and multinomial response models for counts.
Let ci denote the level of consumption per household, z denote the poverty line, and si = ci / z be the normalized welfare indicator per household. The household poverty indicator is determined by the normalized welfare function as follows:
yi = 1 if 1nsi <
0
yi = 0 if 1nsi ³ 0.
The households are observed in n sites that form a
subset S of the space. Each point (household) i has a binary
response yi and a vector k × 1 of covariates
xi. The responses constitute a map
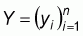 .
.
The regression model is called autologistic and states the conditional probability pi that yi is equal to 1, given all other site values yj (j ¹ i):
|
|
(12) |
where N (i)is the neighbour set of site i
according to a neighbourhood structure and
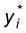 is the sum of the values of
the dependent variable of the neighbours of the site i, that
is:
is the sum of the values of
the dependent variable of the neighbours of the site i, that
is:
|
|
(13) |
where i @ j denotes that the households i and j are neighbours.
This kind of model then takes into account the spatial distribution of the welfare indicator, incorporating the neighbourhood structure in the model as another parameter to estimate.
In the model, XH is the vector of explanatory variables that describe the household characteristics, XC is the vector of explanatory variables that describe the characteristics of the area in which the households reside, and F is a cumulative distribution function that is standard normal in the case of probit regression.
For a given poverty line and a given set of observation on XH and XC, the estimates of bH, bC and g can be obtained by the maximum pseudo-likelihood method. Besag (1975) has demonstrated that the pseudo-likelihood method produces consistent parameter estimates under regular conditions.
Given the above generalized linear model, a maximum
pseudo-likelihood estimator (MPE) for the unknown parameter vector q = {b0,
bH, bC, g} will
be defined as the vector 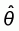 that maximizes the pseudo-likelihood function:
that maximizes the pseudo-likelihood function:
|
|
(14) |
As a result, the function in Equation 14 is not a full likelihood. An analytical form of the full likelihood is intractable for this problem because there is generally an unknown normalizing function.
Therefore, the pseudo-likelihood estimation procedure proposed is an intuitively plausible method that avoids the technical difficulties of the full maximum likelihood approach. Adrawback of the method is that its sampling properties have not been studied as extensively as those of the full maximum likelihood estimators.
Besag (1977) discusses the consistency and efficiency of pseudo-likelihood estimation for simple spatial Gaussian schemes. Strauss and Ikeda (1990) have shown that, for a logit model, maximization of Equation 14 is equivalent to a maximum likelihood fit for a logit regression model with independent observations yi. Consequently, estimates can be obtained by using an iteratively reweighted least squares procedure.
Therefore, any standard logistic regression routine can be used to obtain MPEs of the parameters. However, the standard errors of the estimated parameters calculated by the standard programs are not directly applicable because they are based on the assumption of independence of the observations.
The next step is the estimation of the incidence of poverty in all counties. These estimates are made on the basis of the relationship between the area characteristics and the probability that households residing in these areas are poor. The probability that households in a given county are poor is estimated only on the basis of the area characteristics:
|
|
(15) |
where bH and bC are the coefficients from Equation 12 and pC is the probability that a household drawn from a certain county is poor. Therefore, the parameter estimates from the regression are applied to the census data in order to obtain an imputed value for pC, the percentage of poor households in a county. In this way, the poor households in all the counties are estimated. Finally, using the information on household size, the probability of a household being poor can be extended to the probability of an individual being poor.