The first step in any survey programme should be to make a complete list of all the objectives of the survey, then identify the specific data requirements and priority for each objective. These objectives will dictate the general design of the survey in terms of area, seasonal coverage, gear, etc., and all these must then be balanced against practical constraints such as available vessel and gear, and manpower. The choice of trawl is one of the most important decisions and the optimum trawl design will depend on the size and type of vessel, available manpower, major species sought, type of bottom to be trawled, etc. If there is no previous experience with trawling in the area then the first year might best be spent testing several candidate trawls.
The next step is to choose the area, season(s), depth range, and habitat types to be sampled on the basis of the distribution of the species populations of major interest. In the case of a long-time series some provision should be made for possible shifts in fish distribution, and for sampling as many of the principal species (in terms of biomass) of potential interest as is possible. That is, pelagic as well as demersal species should be considered (many pelagics are vulnerable to bottom trawls at certain times of day in some season), and an adequate geographic and depth range should be covered to account for probable future expansion of fisheries. The fringes of the survey area could be sampled lightly at the beginning of the time series and then intensified later as required.
Usually it will not be possible to collect all of the desired biological information at every station. Care must be taken to ensure that the most important information is collected first and then lower priority data may be collected as time allows. The basic minimum information at each station should include an accurate estimate of the total weight and length frequency of major species; a small sample may suffice to estimate weight and length frequency of other species of lower priority. Other biological studies (e.g., food habits, meristic studies) can use up a great deal of time and manpower, and it is usually necessary to establish reasonable limits on these types of sampling in order to ensure adequate coverage for the basic population survey. Growth and mortality estimates of recruited sizes can often be obtained more cheaply from routine sampling of commercial catches. In general, it is desirable to minimize costs by avoiding sampling more than is necessary to meet objectives.
Properly designed sampling procedures applied over a time series of surveys can provide extremely valuable information even if the amount of sampling is small on any one survey-for example, information on age and size at maturity, seasonal development of gonads, qualitative observations on food of major predators, etc. The value of making a list of all the long-term objectives of the survey is that it is less likely that important types of sampling may be omitted.
Once the objectives of a trawl survey are specified in terms of fish populations to be sampled (in terms of area, season, depth range or habitat types) and the mode of sampling (trawl type, vessel, etc.) is specified, then the total area to be sampled is divided into equal-size non-overlapping sampling units. The actual area of bottom swept by a single trawl haul represents the basic sample unit and it is very small (.01 mi2 in surveys on the US east coast) relative to the total area of the survey. In fact it is so small that the total number of such units in the survey area is virtually infinite. In practice, however, each individual sampling unit is usually defined as a square or rectangular just large enough so that a standard trawl haul in any direction from the centre point will stay within the rectangle; for example, in US surveys the sampling units are rectangles (5' Lat. × 10' Long.) about 38 mi2 in area. The sampling units are then grouped together into larger areas (usually called strata) whose geographic and depth boundaries are chosen on the basis of the density distribution of the fish. The process of stratification is treated in more detail in the section on stratified random sampling. The complete list of all sampling units is called the frame in sampling theory, and is equal to the total survey area in this case. Normally only one trawl haul is made in any one sampling unit and the manner in which these sampling units (hereafter called trawl stations) are selected is of critical importance in the design of trawl surveys.
Proper sample design can provide measures of relative abundance (catch-per-unit-effort) which are unbiased in the sense that they are representative of the entire population of interest and can be compared from one year or season to the next. In addition, it is important to have a statistically valid measure of sampling errors associated with the mean catch per haul index to help interpret the significance of differences observed between areas, seasons, and years. In order to achieve these properties random preselection must be used in locating trawl stations. However, the optimum selection procedure which can maximize precision of indices for a given number of hauls will depend on the specific objectives of the survey and the prior knowledge about the density distribution of major species through time and space. A brief review of the major points to consider in sampling design of trawl surveys is given here, and more details are presented in the papers referenced in this document.
The final product of a trawl survey will be an estimate of abundance, i.e., the number of fish per unit area trawled, x. This value is only one of all the possible values which could have been obtained in similar surveys by occupying all the other possible combinations of stations. The entire set of results which could be obtained in theory can be described by a distribution of the random variable x. There are basically two kinds of error associated with x - (1) random sampling error or variance which decreases with size of sample (number of hauls), and (2) systematic error or bias which is independent of sample size. If the variance of x is small, then the estimator is said to be precise; but it may not necessarily be a good estimator if it has a large bias. The bias of the estimate of abundance is determined by comparing the average value of all possible estimates of x, i.e., the expected value of x or E(x), to the true abundance, μ. If E(x) = μ then the estimate is unbiased, but if E(x) is not equal to μ, then the estimate is biased, i.e., there is a systematic error in the estimate.
The overall quality of an estimator or its accuracy is related to both bias and precision, and can be measured by what is called mean square error. It can be demonstrated that the mean square error is equal to the sum of two terms, the square of the bias (x-μ) and the variance, i.e.,
E(x-μ)2 = (x-μ)2 + Var(x)
In referring to the accuracy of trawl survey data, it is useful in an intuitive sense to keep the two types of error (bias and variance) separate. The greater the number of trawl hauls the closer the mean catch per haul index will be to the value which would be obtained if all possible trawl hauls were made, i.e., the higher the precision. However, even if all possible trawl hauls were made, the mean catch per haul on a unit area basis usually would be considerably less than the true absolute density of fish because the trawl does not catch all the fish in its path. The existence of this generally large bias makes it impossible to use the results of the survey as an absolute index of abundance. However, if the bias remains the same from year to year, then it is possible to use the survey data as a relative index. More precisely, if the bias appears as a multiplicative factor, this factor has to remain constant; that is if E(x) = kμ, then k must remain constant through time in order for the relative abundance index to be a reliable index of true abundance.
It is generally much more difficult to evaluate a bias, or to demonstrate its absence, than to estimate the variance of a sample. If the sample is taken properly it is possible to derive an estimate of the variance from the variability among measurements, within the sample. Information about the bias must be obtained from data independent of the sample.
It is important to know something about the magnitude and the causes of both types of error, bias and variance, in order to maximize efficiency of trawl survey design and to avoid errors in judgement about changes in biomass of fish. There are two major sources of error in abundance estimates derived from trawl surveys: (1) measurement error - related to trawl efficiency or “catchability”, and (2) sampling error - related to spatial variability in the distribution of fish. Because of the importance of this topic, these sources of error in trawl surveys will be considered in more detail.
Measurement error. As noted above, the first type may best be described as a systematic error or bias which arises because the trawl does not catch every fish in its path, i.e., the efficiency of the trawl or “catchability” is less than 1. The “catchability”, or vulnerability as it is sometimes referred to, is defined as the ratio of the number of fish caught to the number present in the area swept by the trawl. Consequently the mean catch per haul on a unit area basis is biased in the sense that it represents only part of the true absolute density of a species depending on the vulnerability or “catchability” of that species to the particular trawl. Catchability coefficients vary widely among different species and thus the bias relative to absolute density is different for each species. Vulnerability of a given species to a given trawl may vary with season, depth, and other less predictable environmental factors, thereby contributing bias to survey abundance indices (mean catch per haul) even on a relative density basis. For example, if vulnerability of a species changes significantly with depth, then a shift in the depth distribution of the species would result in change in the average catchability coefficient, and hence the catch per haul index would be biased relative to the previous survey index. Irregular changes in vulnerability (e.g., shift in vertical distribution due to temperature or feeding conditions) are the most troublesome because often they cannot be detected without population information independent of the survey or until at least one more survey is conducted in a time series. Further consideration of the magnitude and measurement of such biases is given in section 2.6, but it is important to keep in mind that they can be large relative to the variability of abundance indices derived solely from non-uniformity in distribution of the fish.
Small variations in trawl efficiency or vulnerability among hauls on a given survey could be considered random errors and in that sense, measurement errors would contribute to variance. However, these errors are very small relative to the biases identified, and in any case are incorporated into the variance discussed in the next section.
Sampling error. The second major type of error is random sampling error or variance, and this is due to the fact that fish are not distributed uniformly but instead are distributed contagiously (i.e., in clumps) which results in high variability of catches even in repeated hauls at the same station. For example, Barnes and Bagenal (1951) reported coefficients of variation as high as 75 percent for numbers of a single species caught in replicate hauls at a single trawling site. As the number of hauls increases the variance of the sample mean decreases (hence precision increases) but due to the contagious distribution of the fish, a very large number of hauls is needed to achieve high precision (Grosslein, 1971; Sissenwine and Bowman, 1978).
In addition to random sampling error, it is important to keep in mind that the sampling coverage can result in large biases if any significant part of the stock area cannot be trawled. In such circumstances it is common to extrapolate density from the sampled area. However, this obviously can introduce a bias, and the bias could vary from year to year if the relative population density or composition in sampled and non-sampled areas changes.
Summary. The previous discussion is summarized in Table 1 which characterizes the two major sources of error in trawl surveys in terms of the relative significance of bias as against precision and feasibility of estimating the magnitude of the errors.
Since it is well known that fish are not distributed uniformly over any area large enough to encompass an entire population, simple random sampling is seldom used in trawl surveys. A simple random sample from a large geographic area will result in some stations being very close together while some relatively large areas are not sampled at all. Intuitively it is obvious that regular grid pattern of stations would be more satisfactory and this corresponds to systematic sampling. If the major objective of the survey is to define the density gradients in fish distribution (e.g., with respect to depth or temperature) then a uniform grid of stations or series of cross-shelf transects will generally be the most efficient pattern. However, if the objective is to estimate mean abundance, then the appropriate choice between random and systematic sampling is more complicated.
| Source of error | Precision | Bias | |||
|---|---|---|---|---|---|
| Magnitude | Estimation | Magnitude | Constancy | Estimation | |
| Sampling errors | Large variance related to microscale clumping in distribution | Can be estimated from survey data, and variance decreases with sample size | Can be large if only part of stock area can be trawled | If survey coverage incomplete, bias can change if relative abundance in sampled and non-sampled areas changes | If survey coverage incomplete, cannot estimate bias without ancillary information |
| Measurement errors (efficiency of gear or vulnerability) | Small variance relative to above | Generally not estimable, but included in above estimate of variance | Generally large bias, trawl catches under-estimate true density | Can be substantial changes in bias, particularly from changes in vertical distribution | Cannot estimate bias without external information |
In comparison with simple random sampling, systematic sampling has a major shortcoming in that it is difficult to arrive at a valid estimate of the overall sampling variance without using sophisticated methods (Matheron, 1965) or making simplifying assumptions (Cochran, 1977). Another disadvantage of systematic sampling is that it can lead to biased estimates of abundance if there are unknown regularities in the pattern of density distribution or sharp density gradients. For example, if there were a narrow band of hard bottom at a given depth with a unique fish fauna, then a sparse grid could miss it entirely; and if the exact same grid were used for each survey there would be a permanent bias in the results. Besides these problems, systematic sampling may be more or less precise than random sampling depending on the actual distribution of the population. In most cases trawl surveys cover very large areas (thousands of square miles) representing a wide range of depth and consequently a large gradient in the density of fish. On this large scale, trawl catches at stations far apart, especially in terms of depth, will differ much more than catches of stations close together. On the other hand, on a small scale (hundreds of square miles), most of the difference between stations will be due to the “patchiness” effect or contagious distribution of the fish, i.e., two hauls very close to each other will be almost as different as two hauls 10 miles apart, providing they are all in the same depth zone and bottom type. The “patchiness” effect is the fundamental reason why trawl catch data are so variable and it is discussed further in section 2.7. The important conclusions here regarding systematic as against random selection of stations are that:
on a large scale it is desirable to spread the stations apart rather uniformly, i.e. approach a systematic sample design.
on a small scale, random sampling is preferable because it is easy to calculate a valid estimate of variance and there is no risk of bias; and the possible improvement in precision, if any, of systematic as against random sampling will be small.
In such a context, there are clear advantages to stratified sampling where strata are defined according to depth and geographic location. On a large scale stratified sampling will generally be more precise than systematic sampling because it can take account of the available knowledge of density gradients, especially in relation to depth. Within a stratum, providing it is not too large, simple random sampling will be nearly as precise as systematic sampling and it will allow simpler variance calculations.
On most continental shelves of the world, large changes in depth (and hence composition and density of fish populations) occur over cross-shelf distances of 50 km or less. Under these circumstances and given proper depth stratification and allocation of sampling effort for priority species, stratified random sampling will often give higher precision than a simple grid pattern, and it will also have the other advantages of valid variance estimates and unbiasedness. In some cases, systematic sampling may still be more precise but the differences in precision are likely to be small. For example, comparisons of precision achieved on trawl surveys of rock-fishes in Queen Charlotte Sound, British Columbia, showed that on a scale of 80 km, systematic sampling was more precise than stratified random sampling, but the difference was slight (Lenarz and Adams, 1980). In general, for the purpose of estimating abundance, the risk of lower precision with stratified random as against systematic sampling in trawl surveys, will be more than outweighed by the benefits of stratified random sampling.
Fish are seldom distributed uniformly and in most cases are much more abundant at certain depths and geographic locations. With stratified random sampling it is possible to arrive at valid estimates of the mean abundance and its variance, and at the same time utilize the available information on fish distribution to increase the efficiency of sampling in terms of smaller variance relative to simple random sampling.
In general, with stratified random sampling an unbiased estimate of the population density (ignoring systematic measurement errors) is the weighted average of the sample stratum means, i.e., the stratified mean catch per haul:
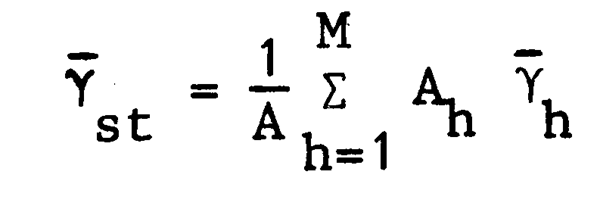
| where | Ah = area of stratum h |
 h = sample mean of stratum h h = sample mean of stratum h | |
A = total survey area =  |
An unbiased estimate of the variance of the stratified mean is likewise a weighted average of the variance estimates from the individual strata:
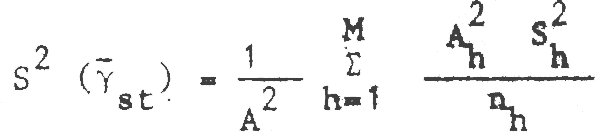
| where | S2h = sample variance of stratum h |
| nh = number of tows in stratum h | |
| M = number of strata in survey area |
The improvement in precision of stratified random sampling over simple random sampling comes about through proper selection of strata and allocation of sampling effort among strata. Basically strata are constructed in accordance with the density distribution of the sample elements, where distribution within each individual stratum is relatively homogeneous compared with other strata. That is, high-medium-low densities are separated into different strata. Optimum allocation of sampling effort in terms of maximum precision for fixed sample size (or minimum sample size to achieve specified precision) is achieved in general by sampling in proportion to the stratum standard deviation (Sh).1 The general theory of stratified sampling including a description of principles of stratum construction and optimum allocation is described by Cochran (1977).
For trawl surveys, stratification is accomplished by subdivision of the survey area
into subareas (sets of sampling units) called strata which represent different levels of
abundance of the priority species. Since the standard deviation is proportional to mean
abundance for trawl catch data, variances will be much higher in strata with high abundance.
For a given total number of hauls greater efficiency can then be achieved in terms of higher
precision (smaller standard deviation) of the stratified mean by allocating more stations
to strata with higher abundance. The optimum allocation of sampling effort will be to sample
each stratum in proportion to its standard deviation. In the absence of prior information
on stratum variances or abundance, a good rule of thumb is to allocate sampling effort in
proportion to stratum areas; this will almost always yield greater precision than simple
random sampling and in most cases it will be fairly close to optimum allocation for multispecies
surveys.
1 or better, in proportion to the product of the stratum size and standard deviation (AhSh)
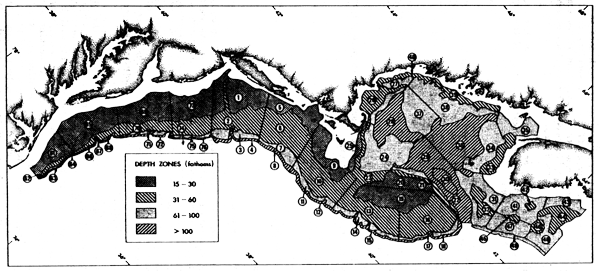
Fig. 1 Sampling strata used in US bottom trawl surveys in the New England region (1 fathom = 1.8288 m)
Depth and habitat (bottom type) are the two principal factors related to demersal fish distribution which are usually used for establishing stratum boundaries. The optimum size and boundaries of strata depend on the intensity of gradients of fish density in relation to these factors both in the offshore and alongshore directions. The stronger the gradients, the smaller the strata (and hence larger number of strata) required to achieve maximum precision for fixed sample size. On most continental shelves the cross-shelf density gradients of demersal fish are usually much steeper than alongshore gradients. This is because distribution of bottom fish is closely correlated with depth and with habitat types (e.g., rocky areas or coral outcrops as opposed to finer sediment areas) which are also correlated with depth. Depth boundaries of strata are usually based on general knowledge of fish distribution against depth and temperature since precise a priori knowledge of habitat distribution is seldom available. Since cross-shelf gradients are steeper than alongshore gradients, the distance between stratum depth boundaries should be much smaller than the distance between cross-shelf stratum boundaries, i.e., strata should normally be longer in the alongshore direction than they are wide in the cross-shelf direction to be consistent with the density distribution of the fish. In practice, rather more strata are usually formed in the alongshore direction than are needed according to the alongshore density gradients, because there is nearly always interest in monitoring alongshore shifts in fish distribution. It is, of course, essential to take into account the major alongshelf changes in habitat or fish distribution such as are associated with large estuaries, capes, canyons, etc. A practical lower limit to the size of strata is the need for at least two stations per stratum so that a variance can be estimated. However, catches are so variable that it is desirable to construct strata with no less than 4–5 hauls so that means and variances will have more than the minimum level of precision.
Since different species have different distribution patterns, it is rarely possible to define a single set of strata which will be optimum for more than a few species. Therefore, in multispecies surveys compromises must usually be made utilizing the combined distribution pattern according to depth and geographic area of the 8–10 most important species. Note that importance will depend on economic value as well as biomass, and the same rule of thumb noted above (sampling proportional to density of priority species) is appropriate. An example of sampling strata used in trawl surveys on the US east coast is given in Figure 1.
Once the strata are established then a choice must be made between random versus systematic sampling within strata. There are no absolute criteria for deciding which is the best. However, the following guidelines can be used. If it is considered important to continue to measure depth distribution of fish within strata (e.g., if strong variable temperature gradients are anticipated) then for this purpose a systematic pattern (regular spacing) of stations will be more efficient than a random pattern. If depth distribution within strata is not critical (and most of the depth and temperature effect should be accounted for already if stratification is done properly) then random sampling will have the advantages of providing simple estimates of variance as well as unbiased estimates of mean (relative) abundance through sampling each habitat with probability proportional to the area covered by that habitat within the stratum.
In some cases practical matters may dictate the sample design. For example, navigation equipment on the research vessel may not be adequate for precise location of stations required by stratified random sampling; in such cases a series of transects from known shore points and use of depth sounders to locate trawling locations may be the only feasible method. Also hydrographic and plankton sampling may be done concurrently with trawling surveys and trawl station patterns could be influenced accordingly.
Whatever the pattern of stations within strata, random or systematic, stratified sampling nearly always has advantages for trawl surveys through:
improved precision with proper allocation over simple random sampling
flexibility in allocation (to account for changes in density distribution of fish) without sacrificing unbiasedness or comparability of annual or seasonal abundance indices
control of overall sampling pattern in survey area to whatever degree of uniformity is desired (by controlling size and location of strata) without sacrificing unbiasedness or flexibility of allocation
ability to estimate abundance in any pre-chosen subsets of strata.
It should be noted again that here the term unbiasedness is used in the sense that all habitats be sampled proportionately totheir area within the stratum. If a stratum is relatively homogeneous with respect to habitat type or other environmental factors which strongly affect distribution of priority species, then risk of bias from systematic rather than random sampling within the stratum will be small. Other sources of bias are much more serious and are discussed in the next section.
As noted earlier, the first and most important point to remember about trawl catches is that they do not catch all of the fish in their path. The actual proportion of fish caught in a given area swept by a given trawl (called catchability coefficient in this report) varies for each species according to its behaviour, e.g., depth distribution relative to vertical height of the trawl, escapement reactions, burrowing habits, etc.; and behaviour of a given species usually varies with time of day, season, and other less regular environmental variables such as food availability or unusual temperature conditions. Equally important is the fact that the catchability coefficients for given species in a given area can be quite different for different trawls or even for the same trawl rigged or fished in a slightly different manner.
The objective in a survey series for monitoring population abundance is to minimize changes in catchability coefficients from both environmental and trawl-related factors, so that the catch per haul index maintains a constant proportionality to the absolute population size. Changes in both environment and trawl performance can introduce large and undetected biases to the catch-per-haul index. Therefore, the importance of minimizing these effects cannot be overemphasized.
A critical element in any survey is the initial selection of the proper trawl. Many factors must be considered in choosing the optimum gear. Among the most important are:
can all the principal target species be caught in adequate numbers for the survey objectives (e.g., headrope height, bottom tending characteristics, etc.)?
is the trawl suitable for all the bottom types in the survey area?
can the trawl be fished effectively by the available vessel?
can the trawl be handled and maintained properly by the available crew?
is there a reliable long-term source of supply for trawl and rigging components (trawl design, twine type, rollers, and especially otter doors)?
Once a survey trawl is chosen then it is critical to maintain exact standard specifications of trawl construction and fishing methods throughout the survey time series. Seemingly slight changes in the construction or rigging of a standard trawl can make major changes in trawl performance; careless repairs of damage during fishing operations could jeopardize results of an entire cruise. The fishing method also must be standardized in every aspect because such aspects as scope, speed of tow, and vessel can drastically alter the fishing performance of any given trawl. It is important to note that a particular vessel x trawl combination is a unique sampler; the same trawl on a different vessel may perform quite differently. Each standard trawl should be tested with instruments (for wingspread, headrope height, doorspread, bottom tending) to ensure standard performance before it is used on a survey; ideally trawl performance should be monitored continuously haul-by-haul during the course of the survey. It is beyond the scope of this report to treat these problems comprehensively. Further details on these aspects of surveys may be found in the published manuals cited earlier and in two more recent unpublished reports (Doubleday, 1981; Sissenwine, Azarovitz and Suomala, 1981). The critical point to be emphasized is that every feasible stepmust be taken to standardize trawl performance otherwise there will be a high risk of confounding changes in trawl performance with true abundance changes, and it will be more difficult to detect environmentally-caused changes in catchability.
If an independent measure of population size is available (e.g., from a virtual population analysis, VPA) over a period of years corresponding to that of the trawl survey then it is possible to calculate a catchability coefficient. For example, Clark and Brown (1977) estimated catchability coefficients for trawl surveys off the US east coast by relating the trawl survey catch per haul to VPA population estimates (i.e., the average proportion of total stock caught in a single standard haul). Expressing their coefficients in terms of the average proportion of fish caught in the path of the trawl gives coefficients ranging from less than .001 to more than .75 for six major species (Table 2). These ratios should be looked upon only as examples.
They are representative of the results from standard multispecies surveys on the US northeast coast. These surveys employ a relatively small (vertical height) trawl, with large rollers or bobbins, and they extend beyond the depths and geographic areas occupied by any one species. Larger ratios for certain species would be obtained with more efficient trawls, e.g., with higher vertical openings relative to off-bottom species or with ground chains instead of bobbins relative to groundfish such as flounders. Also larger ratios would have been obtained if the sampling strata, where the individual species were scarce or absent, had been excluded from the calculation. Note also that the ratios were different for different stocks of the same species which occupied different parts of the same region. The differences appeared significant at least for the cod and silver hake stocks judging from the coefficients of variation for the weighting coefficients (see Table 12, Clark and Brown, 1977) from which the catchability coefficients of Table 2 were calculated. Note that errors in VPA estimates as well as variability in catchability are incorporated into these coefficients. Also note that the catchability coefficients for pelagic species (e.g., herring) are very small relative to the demersal species; this is often the case and poses special problems in analyses of abundance trends of pelagic species as discussed below. Finally, it should be noted that these catchability coefficients are for autumn surveys only; the coefficients vary with the season particularly for the pelagic species.
Turning now to environmentally-caused changes in catchability, it is important to recognize that season and time of day can cause large changes in vulnerability for some species, and some species may not be available at all to bottom trawls during certain seasons. Surveys should be conducted at a season when catchability of principal species is fairly stable, e.g., conducting surveys during active migration periods is not advisable unless the objective is to monitor the migration. In order to maximize comparability of surveys they should be conducted at the same season (or seasons) each year. Diel variations in vulnerability are observed for many species and the differences between day and night catches can be very large (e.g., Sissenwine and Bowman, 1978). Such differences average out for a large number of tows (≥ 100 say) on a continuous 24-h survey design and therefore usually do not need to be accounted for on a total survey abundance index. However, they can be extremely important when analysing results based on a small number of hauls.
Large and unpredictable anomalies in catchability occur from time to time for both pelagic and demersal species (e.g., see Anderson, 1979) and therefore drastic departures from an average level or trend in the survey abundance index should be treated with considerable caution. The risk of serious bias is much greater for species for which the catchability coefficient is very low, since a relatively small change in vulnerability can cause a very large proportional change in catch per haul; this is why it is important to choose a trawl which is efficient for all the priority species. Usually it will be possible to distinguish the larger anomalies from true abundance changes by analysis of population (length/age) structure.
| Species | Stock component | Catchability coefficienta |
|---|---|---|
| Haddock | 5Ze (1963–68)b | .317 |
| 5Ze (1969–74) | .156 | |
| Cod | 5Z | .212 |
| 5Y | .767 | |
| Silver hake | 5Ze | .012 |
| 5Zw-6 | .032 | |
| Red hake | 5Ze | .099 |
| 5Zw-6 | .055 | |
| Yellowtail flounder | 5Ze | .262 |
| 5Zw | .387 | |
| Atlantic herring | 5Z6 | .0008 |
| 5Y | .003 |
a Catchability coefficients were derived from Table 12, Clark and Brown, 1977,by multiplying their untransformed weighting coefficients by a factor equivalentto the stock area in square miles times 100 (since the standard US trawl haul covers approximately .01 square miles); this simply coverts theirweighting coefficient to the ratio of the survey biomass estimate (by thearea swept method) to the VPA biomass estimate; this is approximately equalto the average proportion of fish caught in the path of the trawl.
b Catchability coefficients appeared to decrease for haddock as the populationdeclined and shifted to a younger age structure (see Clark and Brown, 1977,for details).
As indicated earlier, fish are contagiously distributed (clumped) rather than randomly or uniformly distributed in space. The consequence of this clumping is that the variance of the distribution of catch per haul data is much larger than the mean, which indicates that large sample sizes will be required to obtain high precision. The distribution which generally fits trawl survey data is the negative binomial distribution (Taylor, 1953). The mean and variance of the negative binomial distribution are related as follows:
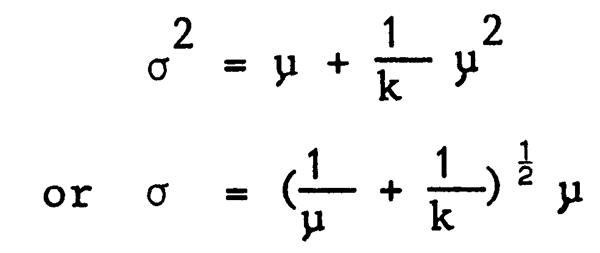
where μ and σ2 are the mean and variance and k is a coefficient related to the degree of positive skewness in the distribution. For a fixed value of k, and for relatively large (with respect to 1/k) values of μ, the relationship of σ and μ is approximately linear. Empirical information from trawl surveys confirms that the standard deviation is linearly related to the mean and suggests that for a given species, k tends to be constant over time and various population levels (Pennington and Grosslein, 1978). It should also be noted that μ increases linearly with sample-unit size (tow duration) at least up to the point of gear saturation, but that k appears relatively independent of the size of sample unit.
One of the consequences of sampling from a highly contagious distribution is that little precision will be gained by increasing the size of the sampling unit (area swept by a single trawl haul in this case) beyond some modest level. This may be shown by plotting the coefficient of variation (C = σ/μ) for the negative binomial and assuming a fixed k:
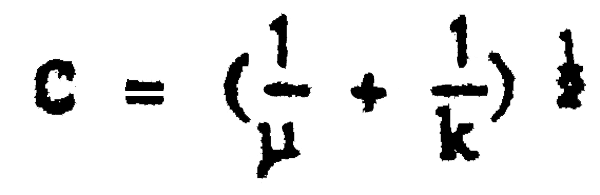
Although C decreases with increase in μ it rapidly reaches a point of diminishing returns and does not go to zero no matter how large μ becomes (Pennington and Grosslein, 1978). In general, for fixed sampling-unit size, C will be large for species for which k and μ are small, i.e., species for which clumping or schooling is very pronounced and mean catch per haul is small. Lenarz and Adams (1980) showed that trawl duration had relatively little effect on precision of abundance indices of rockfish in comparison with the number of trawl hauls.
These properties must be taken into account in order to maximize precision in a trawl survey. The problem is basically to select a sample size (number of hauls) and a sampling-unit size (duration of each haul) which will give highest precision for the total time available for the survey. The total time for each survey is usually fixed, and in practice length of tow is chosen on the basis of the size of catches, and then as many hauls are made as time allows. Assuming you have some information on the time required to set and retrieve the trawl, and on the value of k and the relation between catch and tow duration for the major species, it is possible to approximate the optimum duration of haul for each species. Estimates of optimum tow length varied from 2 to 45 minutes for several species on Georges Bank (Pennington and Grosslein, 1978). In general, the optimum tow length is higher for less abundant species, and it will increase for a given species as stock abundance declines. Optimum tow length in a multispecies survey involves a compromise representing the Characteristics of all the major species. Also there are important practical considerations such as the size of catches of major species in relation to tow duration. Average catches should be large enough to provide all the data required for the objectives of the survey, but not so large that they require inordinate amounts of processing time or result in gear saturation. Tow durations of 30–60 min are commonly used in trawl surveys. Tows of 30 min are used in surveys on the US east coast, which falls within the range of estimates for optimum duration noted above (Pennington and Grosslein, 1978).
An obvious way to increase precision is to increase sample size. Confidence limits (95%) are on the order of ±50% of the mean for areas such as Georges Bank with approximately 70 (30-min) hauls on each survey (Grosslein, 1971). However, to reduce confidence limits to ±30% of the mean, it would be necessary to more than double the number of hauls. Other possible ways of increasing precision include post-stratification to take account of diel differences in catchability, and standardization of distance towed over the bottom on each haul. Possible gains in precision by these means appear relatively modest (Pennington and Grosslein, 1978), and real time control of speed and distance over the bottom require sophisticated instrumentation such as highly precise navigation and/or a Doppler speed log with computer hookup for calculating speed over the bottom.
Probably the best way to maximize precision is to ensure that allocation of sampling effort is approximately proportional to the variability encountered in various sampling strata at least for the 3 or 4 highest priority species. If empirical data on stratum variances are not available then data on average abundance can be used instead since variance is correlated with mean abundance. If fish are rather uniformly distributed or there are very many species on the priority list, then a good rule of thumb is to allocate numbers of stations in proportion to the area of sampling strata.
There are mathematical procedures for calculating the optimum allocation in terms of maximum precision for fixed cost or minimum cost for specified precision (see for example Evans, 1951); however these procedures are difficult to apply in multispecies trawl surveys because of the broad range of objectives and the fact that density distribution varies so widely among different species.