Nine studies have been published of experimentally induced salmonellosis, conducted between 1936 and 1970 using a variety of serotypes and strains. Serotypes and strains used in these series of feeding trials are listed in Table 3.2.
Table 3.2. Human feeding trials that have been performed using Salmonella
| |
Serotype(s) |
Strain(s) |
Reference |
|
1 |
S. Typhimurium |
|
Hormaeche, Peluffo and Aleppo, 1936 |
|
2 |
S. Anatum |
|
Varela and Olarte, 1942 |
|
3 |
S. Meleagridis |
I, II & III |
McCullough and Eisele, 1951a |
|
S. Anatum |
I, II & III |
McCullough and Eisele, 1951a |
|
|
4 |
S. Newport |
|
McCullough and Eisele, 1951c |
|
S. Derby |
|
McCullough and Eisele, 1951c |
|
|
S. Bareilly |
|
McCullough and Eisele, 1951c |
|
|
5 |
S. Pullorum |
I, II, III & IV |
McCullough and Eisele, 1951d |
|
6 |
S. Typhi |
|
Sprinz et al., 1966 |
|
7 |
S. Sofia |
|
Mackenzie and Livingstone, 1968 |
|
8 |
S. Typhi |
Quailes, Zermatt, Ty2V, 0-901 |
Hornick et al., 1970 |
|
9 |
S. Typhi |
Quailes |
Woodward, 1980 |
Although the list of human feeding trials for Salmonella in humans is more extensive than may exist for other bacterial pathogens, some of these studies were deemed to be unsuitable and were not used in further analysis to derive conclusions about the pathogenicity of Salmonella in general in humans. The earliest study used 5 subjects, who were all fed a dose of approximately 9-logs in water and all exposed individuals were subsequently infected (Hormaeche, Peluffo and Aleppo, 1936). In a later study (Varela and Olarte, 1942), apparently only one volunteer was used, who became ill after ingesting a dose of 10-logs in water. The study conducted by MacKenzie and Livingstone (1968) involved a nasal inoculation of approximately 25 cells in one volunteer, who subsequently became ill. These three studies were not informative due to the use of only large doses with 100% attack rates, the testing of only one dose with one subject, or the method of inoculation. Studies conducted using S. Typhi (Sprinz et al., 1966; Hornick et al., 1970; Woodward, 1980), were considered to be inappropriate in the current analysis, primarily because of the difference between the illnesses caused by typhoid and non-typhoid Salmonella. S. Typhi is highly invasive and causes typhoid fever, a systemic bacteraemic illness, as opposed to non-typhoid salmonellosis, characterized by gastroenteritis and marked by diarrhoea, fever and abdominal pain, with rare systemic invasion.
The most extensive human feeding trials of non-typhoid Salmonella were conducted in the late 1940s to early 1950s (McCullough and Eisele, 1951a, b, c & d). Six different Salmonella serotypes were used, with up to 3 or 4 different strains of some of the serotypes. The subjects used in the feeding trials were healthy males from a penal institution. Feeding trials using S. Pullorum I, II, III & IV were considered to be inappropriate for deriving estimates about the infectivity of non-typhoid Salmonella for humans, because, as noted by other researchers (Blaser and Newman, 1982; Coleman and Marks, 1998) this is primarily a fowl-adapted strain. It was noted that a dramatically higher dose was required to produce illness using S. Pullorum and the clinical picture of illness, when it did occur, was characterized by an explosive onset and fast recovery (McCullough and Eisele, 1951d). At dosages producing illness, the organism could only be isolated from the stools for the first day or two, and not thereafter. In addition, Fazil (1996) conducted an evaluation of the feeding trial data and found that the dose-response relationship for S. Pullorum was significantly different from the other strains used in the feeding trials.
In order to evaluate the data derived from the human feeding trials, the experimental design used by the researchers is briefly described (McCullough and Eisele, 1951a & c).
Human volunteers
The subjects selected for the experimental feeding trials were healthy males from a penal institution.
According to the authors, chronic complainers and those who had frequent gastrointestinal disturbances in the past were eliminated from the trials.
After an initial selection of volunteers, at least three weekly stool cultures were done.
Only those individuals with no Salmonella or other easily confused organisms in the stools were carried further in the experiment.
An initial serum agglutination test was done against the organism to be administered.
Subjects that showed a moderate or high agglutination titre against a particular organism were in general not used in the experiments with that species.
Source of Salmonella Strains
Strains of Salmonella used in the feeding trials were obtained from market samples of high-moisture spray-dried whole egg powder.
Method of feeding
Cultures for feeding trials were subcultured on trypticase soy agar.
After 24 hours of incubation, the resulting growth was suspended in saline and standardized turbidimetrically.
The dose was administered in a glass of eggnog shortly following the noon meal.
A group of men, usually consisting of six, received the same experimental feeding dose.
Control feedings were provided by eggnog alone or by prior feeding of the test organisms at what the authors observed to be non-infective levels.
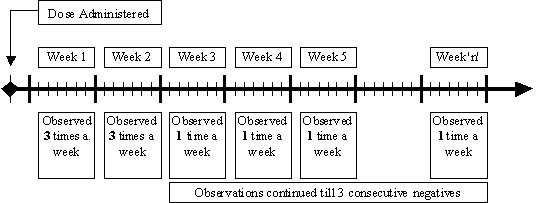
Observations after feeding (Figure 3.1)
Following the feeding, men were interviewed and observed three times a week for a period of two weeks, and once a week thereafter.
Additional visits were made when required by the condition of the volunteer.
Men were questioned with regard to symptoms.
Temperatures were recorded.
Faecal cultures were obtained.
When indicated, blood counts and cultures were also done.
Blood samples for agglutination were drawn at weekly intervals for 4 weeks following feeding.
Faecal samples were collected and cultures were done on all men 3 times a week for the first 2 weeks, after that once a week until at least three consecutive negative samples had been obtained.
Figure 3.1. Scheme for observations during human feeding trial experiments of McCullough and Eisele (1951a, c).
Infection definition (faecal shedding)
Infection was defined as the recovery of the administered strain from faecal samples.
Illness definition criteria
Illness was characterized by the existence of the following two conditions:
Ö documentation of symptoms; and
Ö recovery of the organism from stool (infection);
And one or more of the following:
Ö diarrhoea or vomiting,
Ö fever,
Ö rise in specific agglutination titre, or
Ö other, unspecified, signs.
The feeding trial data have been reviewed and critiqued by various researchers. Blaser and Newman (1982) reviewed the infective dose data for Salmonella and identified several deficiencies:
[1] The feeding of the pathogen to the volunteers was conducted after their noon meal, when gastric acid was probably high.
[2] It was observed that over half the volunteers who became ill had earlier been fed lower doses of the same serotype. These earlier feedings may have confounded the results by introducing a degree of immunity, thus making infection less likely, or, alternatively, the earlier feedings may have had a cumulative effect that made infection more likely.
[3] A failure to assess the minimal infective dose.
[4] The use of too few volunteers at low doses.
In the United States of America Salmonella Enteritidis Risk Assessment in eggs report (USDA-FSIS, 1998) (hereafter generally referred to as US SE RA), additional deficiencies in the feeding trial data were identified:
[1] The use of healthy male volunteers could probably underestimate the true pathogenicity to the overall population.
[2] The size of the groups used at each dose level was relatively small, with 18 of the 22 test doses using less than 6 people.
[3] There were no low doses tested. The smallest dose that was tested was greater than 104 CFU Salmonella bacteria.
[4] The lowest dose that caused an infection was also the lowest dose tested.
Additional points related to some of the critiques should also be noted. While it is true that the feeding of the dose after the noon meal when gastric acid was high could potentially reduce the estimated infectivity of the pathogen (Blaser and Newman, 1982), the dose was administered using eggnog, a high-fat-content medium. The eggnog could have conferred a level of protection against the effects of gastric acid, thus potentially negating the acid effects. It seems reasonable, however, to assume that, given the fact that the subjects used in the feeding trials were healthy males, the infectivity estimated for this population will be some factor less than for the general population, and more so for the more susceptible members of the general population. Overall, the criticisms of the feeding trial data are for the most part fair in their assessment of the potential biases in the results that may be expected.
The human feeding trial, as described earlier, measured both infection and illness. Most dose-response relationships are developed using infection (faecal shedding) as the dependent variable, primarily out of necessity due to the nature of the data. It should be noted that the use of the infection endpoint in deriving a dose-response relationship could introduce a level of conservatism into the dose-response relationship, depending on how the conditional dependence of illness - which is essentially the output of ultimate interest - following infection is treated. In the human feeding trial, it was also pointed out that approximately 40% of the volunteers that were shedding were reported to be last positive on or before the second day following administration, apparently clearing the infection two days post-administration (Coleman and Marks, 1998). These authors noted that there is some ambiguity in estimating infection based on faecal shedding for less than two days. The available data measuring illness as the endpoint is sparse, without any response being observed until a dose of approximately 6-logs. It has been noted (Blaser and Newman, 1982) that the strict criteria used by the researchers to define illness may have resulted in volunteers with mild complaints being classified as asymptomatic excretors rather than ill subjects. Although concerns have been raised as to the experimental design of the human feeding trials, it is appropriate to consider it at this juncture as still holding value in providing a basis upon which to at least start exploring the dose-response relationship.
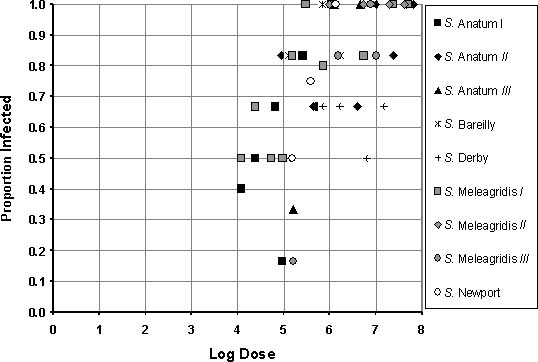
Tables 3.3 to 3.7 present the original data from the McCullough and Eisele studies. These data are also summarized in Figure 3.2.
Table 3.3. Feeding trial data for S. Anatum I, II and III (McCullough and Eisele, 1951a)
|
Serotype |
Dose |
Log Dose |
Positive (Inf)(1) |
Total |
Proportion |
|
S. Anatum I |
1.20E+04 |
4.08 |
2 |
5 |
0.40 |
|
S. Anatum I |
2.40E+04 |
4.38 |
3 |
6 |
0.50 |
|
S. Anatum I |
6.60E+04 |
4.82 |
4 |
6 |
0.67 |
|
S. Anatum I |
9.30E+04 |
4.97 |
1 |
6 |
0.17 |
|
S. Anatum I |
1.41E+05 |
5.15 |
3 |
6 |
0.50 |
|
S. Anatum I |
2.56E+05 |
5.41 |
5 |
6 |
0.83 |
|
S. Anatum I |
5.87E+05 |
5.77 |
4 |
6 |
0.67 |
|
S. Anatum I |
8.60E+05 |
5.93 |
6 |
6 |
1.00 |
|
S. Anatum II |
8.90E+04 |
4.95 |
5 |
6 |
0.83 |
|
S. Anatum II |
4.48E+05 |
5.65 |
4 |
6 |
0.67 |
|
S. Anatum II |
1.04E+06 |
6.02 |
6 |
6 |
1.00 |
|
S. Anatum II |
3.90E+06 |
6.59 |
4 |
6 |
0.67 |
|
S. Anatum II |
1.00E+07 |
7.00 |
6 |
6 |
1.00 |
|
S. Anatum II |
2.39E+07 |
7.38 |
5 |
6 |
0.83 |
|
S. Anatum II |
4.45E+07 |
7.65 |
6 |
6 |
1.00 |
|
S. Anatum II |
6.73E+07 |
7.83 |
8 |
8 |
1.00 |
|
S. Anatum III |
1.59E+05 |
5.20 |
2 |
6 |
0.33 |
|
S. Anatum III |
1.26E+06 |
6.10 |
6 |
6 |
1.00 |
|
S. Anatum III |
4.68E+06 |
6.67 |
6 |
6 |
1.00 |
NOTE: (1) Number found positive (infected).
Table 3.4. Feeding trial data for S. Meleagridis I, II and III (McCullough and Eisele, 1951a).
|
Serotype |
Dose |
Log Dose |
Positive (Inf)(1) |
Total |
Proportion |
|
S. Meleagridis I |
1.20E+04 |
4.08 |
3 |
6 |
0.50 |
|
S. Meleagridis I |
2.40E+04 |
4.38 |
4 |
6 |
0.67 |
|
S. Meleagridis I |
5.20E+04 |
4.72 |
3 |
6 |
0.50 |
|
S. Meleagridis I |
9.60E+04 |
4.98 |
3 |
6 |
0.50 |
|
S. Meleagridis I |
1.55E+05 |
5.19 |
5 |
6 |
0.83 |
|
S. Meleagridis I |
3.00E+05 |
5.48 |
6 |
6 |
1.00 |
|
S. Meleagridis I |
7.20E+05 |
5.86 |
4 |
5 |
0.80 |
|
S. Meleagridis I |
1.15E+06 |
6.06 |
6 |
6 |
1.00 |
|
S. Meleagridis I |
5.50E+06 |
6.74 |
5 |
6 |
0.83 |
|
S. Meleagridis I |
2.40E+07 |
7.38 |
5 |
5 |
1.00 |
|
S. Meleagridis I |
5.00E+07 |
7.70 |
6 |
6 |
1.00 |
|
S. Meleagridis II |
1.00E+06 |
6.00 |
6 |
6 |
1.00 |
|
S. Meleagridis II |
5.50E+06 |
6.74 |
6 |
6 |
1.00 |
|
S. Meleagridis II |
1.00E+07 |
7.00 |
5 |
6 |
0.83 |
|
S. Meleagridis II |
2.00E+07 |
7.30 |
6 |
6 |
1.00 |
|
S. Meleagridis II |
4.10E+07 |
7.61 |
6 |
6 |
1.00 |
|
S. Meleagridis III |
1.58E+05 |
5.20 |
1 |
6 |
0.17 |
|
S. Meleagridis III |
1.50E+06 |
6.18 |
5 |
6 |
0.83 |
|
S. Meleagridis III |
7.68E+06 |
6.89 |
6 |
6 |
1.00 |
|
S. Meleagridis III |
1.00E+07 |
7.00 |
5 |
6 |
0.83 |
NOTE: (1) Number found positive (infected).
Table 3.5. Feeding trial data for S. Newport (McCullough and Eisele, 1951c).
|
Serotype |
Dose |
Log Dose |
Positive (Inf)(1) |
Total |
Proportion |
|
S. Newport |
1.52E+05 |
5.18 |
3 |
6 |
0.50 |
|
S. Newport |
3.85E+05 |
5.59 |
6 |
8 |
0.75 |
|
S. Newport |
1.35E+06 |
6.13 |
6 |
6 |
1.00 |
NOTE: (1) Number found positive (infected).
Table 3.6. Feeding trial data for S. Bareilly (McCullough and Eisele, 1951c).
|
Serotype |
Dose |
Log Dose |
Positive (Inf)(1) |
Total |
Proportion |
|
S. Bareilly |
1.25E+05 |
5.10 |
5 |
6 |
0.83 |
|
S. Bareilly |
6.95E+05 |
5.84 |
6 |
6 |
1.00 |
|
S. Bareilly |
1.70E+06 |
6.23 |
5 |
6 |
0.83 |
NOTE: (1) Number found positive (infected).
Table 3.7. Feeding trial data for S. Derby (McCullough and Eisele, 1951c).
|
Serotype |
Dose |
Log Dose |
Positive (Inf)(1) |
Total |
Proportion |
|
S. Derby |
1.39E+05 |
5.14 |
3 |
6 |
0.50 |
|
S. Derby |
7.05E+05 |
5.85 |
4 |
6 |
0.67 |
|
S. Derby |
1.66E+06 |
6.22 |
4 |
6 |
0.67 |
|
S. Derby |
6.40E+06 |
6.81 |
3 |
6 |
0.50 |
|
S. Derby |
1.50E+07 |
7.18 |
4 |
6 |
0.67 |
NOTE: (1) Number found positive (infected).
Figure 3.2. Summary of feeding trial data (McCullough and Eisele, 1951a; 1951c).
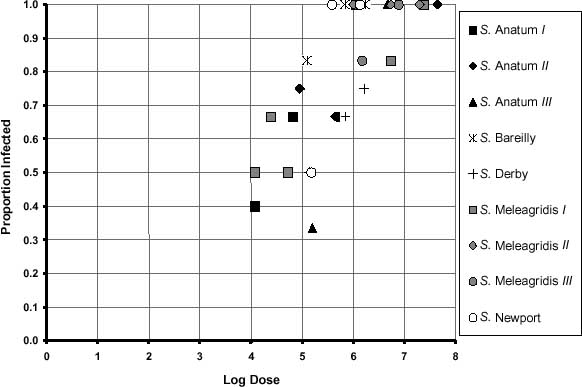
It has also been noted that, in the feeding trials, some of the volunteers were administered doses more than once. The earlier doses, which were lower and at which no response was observed, may have resulted in either a cumulative or an immunity effect. In order to attempt to remove this bias, the doses and subjects at which repeat feedings were conducted were edited out and the data re-evaluated. The edited data for naive subjects only are presented in Tables 3.8 to 3.12, and summarized in Figure 3.3.
Table 3.8. Feeding trial data for S. Anatum I, II and III for naive subjects.
|
Serotype |
Dose |
Log Dose |
Positive (Inf)(1) |
Total |
Proportion |
|
S. Anatum I |
1.20E+04 |
4.08 |
2 |
5 |
0.40 |
|
S. Anatum I |
6.60E+04 |
4.82 |
4 |
6 |
0.67 |
|
S. Anatum I |
5.87E+05 |
5.77 |
4 |
6 |
0.67 |
|
S. Anatum I |
8.60E+05 |
5.93 |
4 |
4 |
1.00 |
|
S. Anatum II |
8.90E+04 |
4.95 |
3 |
4 |
0.75 |
|
S. Anatum II |
4.48E+05 |
5.65 |
4 |
6 |
0.67 |
|
S. Anatum II |
2.39E+07 |
7.38 |
3 |
3 |
1.00 |
|
S. Anatum II |
4.45E+07 |
7.65 |
3 |
3 |
1.00 |
|
S. Anatum III |
1.59E+05 |
5.20 |
1 |
3 |
0.33 |
|
S. Anatum III |
1.26E+06 |
6.10 |
6 |
6 |
1.00 |
|
S. Anatum III |
4.68E+06 |
6.67 |
3 |
3 |
1.00 |
NOTE: (1) Number found positive (infected).
Table 3.9. Feeding trial data for S. Meleagridis I, II and III for naive subjects.
|
Serotype |
Dose |
Log Dose |
Positive (Inf)(1) |
Total |
Proportion |
|
S. Meleagridis I |
1.20E+04 |
4.08 |
3 |
6 |
0.50 |
|
S. Meleagridis I |
2.40E+04 |
4.38 |
4 |
6 |
0.67 |
|
S. Meleagridis I |
5.20E+04 |
4.72 |
3 |
6 |
0.50 |
|
S. Meleagridis I |
1.15E+06 |
6.06 |
6 |
6 |
1.00 |
|
S. Meleagridis I |
5.50E+06 |
6.74 |
5 |
6 |
0.83 |
|
S. Meleagridis I |
2.40E+07 |
7.38 |
4 |
4 |
1.00 |
|
S. Meleagridis II |
1.00E+06 |
6.00 |
6 |
6 |
1.00 |
|
S. Meleagridis II |
5.50E+06 |
6.74 |
6 |
6 |
1.00 |
|
S. Meleagridis II |
2.00E+07 |
7.30 |
3 |
3 |
1.00 |
|
S. Meleagridis III |
1.58E+05 |
5.20 |
1 |
3 |
0.33 |
|
S. Meleagridis III |
1.50E+06 |
6.18 |
5 |
6 |
0.83 |
|
S. Meleagridis III |
7.68E+06 |
6.89 |
4 |
4 |
1.00 |
NOTE: (1) Number found positive (infected).
Table 3.10. Feeding trial data for S. Newport for naive subjects.
|
Serotype |
Dose |
Log Dose |
Positive (Inf)(1) |
Total |
Proportion |
|
S. Newport |
1.52E+05 |
5.18 |
3 |
6 |
0.50 |
|
S. Newport |
3.85E+05 |
5.59 |
4 |
4 |
1.00 |
|
S. Newport |
1.35E+06 |
6.13 |
3 |
3 |
1.00 |
NOTE: (1) Number found positive (infected).
Table 3.11. Feeding trial data for S. Bareilly for naive subjects.
|
Serotype |
Dose |
Log Dose |
Positive (Inf)(1) |
Total |
Proportion |
|
S. Bareilly |
1.25E+05 |
5.10 |
5 |
6 |
0.83 |
|
S. Bareilly |
6.95E+05 |
5.84 |
3 |
3 |
1.00 |
|
S. Bareilly |
1.70E+06 |
6.23 |
3 |
3 |
1.00 |
NOTE: (1) Number found positive (infected).
Table 3.12. Feeding trial data for S. Derby for naive subjects.
|
Serotype |
Dose |
Log Dose |
Positive (Inf)(1) |
Total |
Proportion |
|
S. Derby |
1.39E+05 |
5.14 |
3 |
6 |
0.50 |
|
S. Derby |
7.05E+05 |
5.85 |
2 |
3 |
0.67 |
|
S. Derby |
1.66E+06 |
6.22 |
3 |
4 |
0.75 |
|
S. Derby* |
6.40E+06 |
6.81 |
1 |
3 |
0.33 |
NOTE: (1) Number found positive (infected).
Figure 3.3. Summary of feeding trial data for naive subjects.
This section presents the quantitative information that is available for Salmonella infectivity or illness, from which dose-response relationships can be estimated. It is not possible to provide all the details necessary to give a complete coverage of the theory behind the dose-response relationships in this document. However, a comprehensive treatment of dose-response models and assumptions related to the mathematical derivation of the various equations is given in the FAO/WHO Hazard Characterization Guidelines document (currently in preparation)
Several approaches and models to characterize the dose-response relationship for Salmonella have been presented in the literature or in official reports and documents. This report discusses three different approaches for modelling Salmonella. The first model is the beta-Poisson model fitted to the human feeding trial data for Salmonella (Fazil, 1996). The second model was proposed in the US SE RA and was based on the use of a surrogate pathogen to describe the dose-response relationship. The third model, introduced in the Health Canada Salmonella Enteritidis risk assessment, used a Weibull dose-response relationship updated to reflect outbreak information using Bayesian techniques. In addition to these models, the current analysis also explores the effect of fitting the beta-Poisson model to the human feeding trial data for naive subjects only.
Dose-response model fitted to non-typhi Salmonella human feeding trial data
The human feeding trial data have been analysed using the beta-Poisson, lognormal (log-probit) and exponential dose-response functional forms (Fazil, 1996). Three doses in the data set were identified as "outliers" (i.e. S. Anatum I: 9.3E+5; S. Meleagridis III: 1.58E+5; S. Derby: 6.4E+6) and were subsequently removed from the analysis. The analysis concluded that both the lognormal and beta-Poisson functional forms fit the majority of the data. However, based upon theoretical considerations (threshold vs non-threshold, where threshold models assume that there is some finite minimum dose below which no response can occur, while non-threshold models assume that the minimum possible dose that can cause a response is one cell, even though the probability may be very low for one cell to successfully survive all the host defences), the beta-Poisson model was proposed as the model to describe the dose-response relationship for Salmonella. In addition, it was reported that all the serotypes could be adequately described using a single beta-Poisson dose-response curve. The parameters of the beta-Poisson dose-response model for non-typhi Salmonella in general were reported as alpha = 0.3126, and beta = 2885. The uncertainty in the parameters was estimated using a bootstrap approach, which generated sets of parameters that satisfied the model fitting conditions. The potential for a greater probability of illness for susceptible and normal populations was not addressed in the analysis.
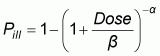
|
Model Used: |
Beta-Poisson |
|
Parameters: |
Alpha = 0.3126 |
|
Comment: |
Uncertainty in the parameters estimated using a bootstrap approach, which generated a set of alpha and beta parameters that could be randomly sampled in order to incorporate uncertainty. |
Dose-response model fitted to non-typhi Salmonella naive human feeding trial data
The model parameters reported by Fazil (1996) did not consider the effect that multiple feedings may have on the dose-response relationship. As a result, for this present review, the data using only naive subjects (Tables 3.8 to 3.12 and Figure 3.3) were re-fitted to the beta-Poisson model and the parameters for this model were estimated. The data were fitted using maximum likelihood techniques, as described by various authors (Haas, 1983; Haas et al., 1993; Regli et al., 1991; Teunis et al., 1996). The parameters of the beta-Poisson dose-response model fitted to the data for naive subjects was estimated to be alpha = 0.4047 and beta = 5587. The uncertainty in the parameters was estimated using the bootstrap approach.
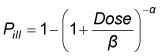
|
Model Used: |
Beta-Poisson |
|
Parameters: |
Alpha = 0.4047 |
|
Comment: |
Uncertainty in the parameters estimated using a bootstrap approach, which generated a set of alpha and beta parameters that could be randomly sampled in order to incorporate uncertainty. |
The beta-Poisson dose-response curves generated using the original dose-response data and the data edited to reflect only naive subjects are shown in Figure 3.4. Also shown in the figure are the feeding trial data to illustrate the fit to the data.
As shown in Figure 3.4, both models fit the feeding trial data well and the difference between the curves using the original data and the data that reflects only naive subjects is small. Interestingly, the curve fitted to the naive data tends to estimate a greater probability of infection at doses above approximately 104 than does the curve fitted to the original data, perhaps reflecting a tendency in the data for a slightly greater susceptibility for naive subjects. Within the lower dose regions, the two curves are very similar, and the dose translating to a probability of infection for 50% of the population is virtually identical for the two curves (2.36E4 vs 2.54E4 for the original and naive models). The low dose extrapolation for the two dose-response curves was also very similar. As a result of the similarities between the models and the concerns that have been raised about potential immunity or cumulative effects, the beta-Poisson model fitted to the data of naive subjects is used in the remainder of this analysis as the representation of the human feeding trial data fitted to the beta-Poisson model.
Figure 3.4. Comparison between dose-response model fitted to original feeding trial data and feeding trial data for naive subjects.
USDA-FSIS Salmonella Enteritidis Risk Assessment
The hazard characterization in the US SE RA evaluates the public health impacts of exposure to S. Enteritidis through shell eggs and egg products in terms of numbers of illnesses and specific public health outcomes on an annual basis. Considerations in quantifying the dose-response relationship included the selection of an appropriate functional form, extrapolation of fitted curves to low-dose ranges, and the use of surrogate organisms in the absence of feeding trial data specific for S. Enteritidis.
In the initial quantification of a dose-response relationship for S. Enteritidis, a beta-Poisson dose-response curve was fitted to the pooled data from all Salmonella feeding trials (McCullough and Eisele, 1951a, c) and the fitted model compared with epidemiological information from available S. Enteritidis outbreak data. The model validation on the epidemiological data showed that outbreaks associated with S. Enteritidis exhibited a higher attack rate than would be estimated using the pooled human feeding trial data for Salmonella. Furthermore, an analysis of variance (ANOVA) on the Salmonella human feeding trial data for dose and serotype effects revealed two distinct, statistically significant dose-response patterns (representative of doses >103 organisms) among the Salmonella serotypes in the human feeding studies data (Morales, Jaykus and Cowen, 1995; Jaykus, Morales and Cowen, 1997).
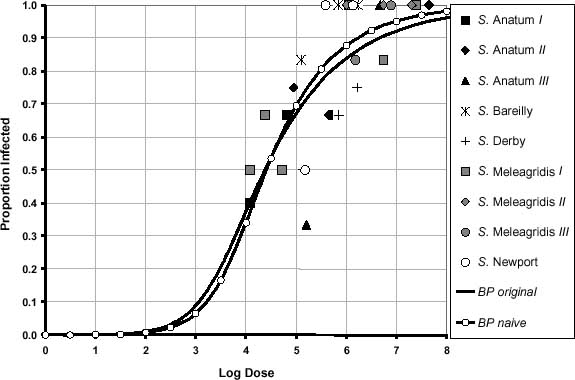
The inability of several dose-response models, fitted to the Salmonella data, to predict the high attack rates associated with low doses, such as the 1994 S. Enteritidis outbreak from ice cream (Hennessy et al., 1996) was likewise previously noted by Morales, Jaykus and Cowen (1995). In order to capture the region of concern (i.e. the low-dose range with corresponding high attack rates evident in the outbreak investigation data), human feeding study data utilizing a low-dose organism was selected for subsequent dose-response modelling as a surrogate for S. Enteritidis. The absence of human feeding study data for S. Enteritidis prompted the selection of Shigella dysenteriae (Levine and DuPont, 1973) as a proxy for modelling "low-dose" Salmonella serotypes (attack rates >0 with doses = 103 organisms).
Epidemiological evidence from outbreak investigations was once again used to conduct a model validation check on the two dose-response models generated (beta-Poisson curves fitted to human feeding trial data for pooled Salmonella species and to the low-dose proxy Shigella dysenteriae). A review of the epidemiological outbreak investigations showed that many of the reported doses resulting in illnesses were several orders of magnitude lower than the doses reported in the Salmonella feeding trials. Further, the doses which caused outbreaks were likewise several orders of magnitude lower than the doses which were predicted by the dose-response models constructed from the Salmonella feeding trial data. Model validation to the available outbreak investigation data subsequently served as the basis for selection of a dose-response relationship (Figure 3.5). The outbreak investigation data used for dose-response model validation are detailed in Table 3.13.
Figure 3.5. USDA comparison of available Salmonella outbreak investigation data and beta-Poisson dose-response curves for Shigella dysenteriae estimated for normal and susceptible subpopulations (USDA-FSIS, 1998).
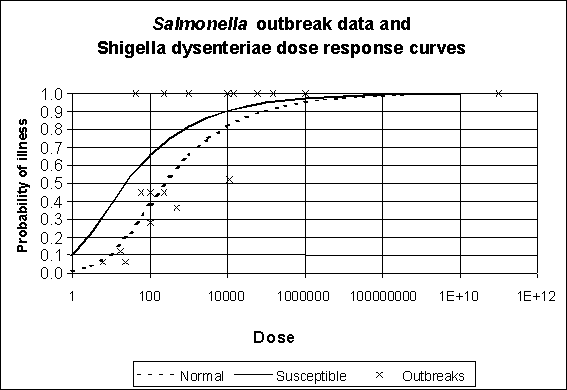
Table 3.13. Salmonella outbreak investigation data used in the US SE RA to compare with Shigella dose-response curves (USDA-FSIS, 1998).
|
Serovar |
Dose |
Log dose |
Number ill |
Attack rate |
Reference |
|
Typhimurium |
1.7E+01 |
1.23 |
16 000 |
12% |
Boring, Martin and Elliott, 1971 |
|
Schwarzengrund |
4.4E+01 |
1.64 |
1 |
100% |
Lipson, 1976 |
|
Newport |
6.0E+01 |
1.78 |
48 |
45% |
Fontaine et al., 1978 |
|
Eastbourne |
1.0E+02 |
2.00 |
95 |
45% |
D’Aoust et al., 1975 |
|
Heidelberg |
1.0E+02 |
2.00 |
339 |
28% |
Fontaine et al., 1980 |
|
Heidelberg |
2.0E+02 |
2.30 |
1 |
100% |
George, 1976 |
|
Newport |
2.34E+02 |
2.36 |
46 |
45% |
Fontaine et al., 1978 |
|
Heidelberg |
5.0E+02 |
2.70 |
339 |
36% |
Fontaine et al., 1980 |
|
Typhimurium |
1.1E+04 |
4.04 |
1 790 |
52% |
Armstrong et al., 1970 |
|
Cubana |
1.5E+04 |
4.18 |
28 |
100% |
Lang et al., 1967 |
|
Cubana |
6.0E+04 |
4.78 |
28 |
100% |
Lang et al., 1967 |
|
Zanzibar |
1.5E+05 |
5.18 |
6 |
100% |
Reitler, Yarom and Seligmann, 1960 |
|
Infantis |
1.0E+06 |
6.00 |
5 |
100% |
Angelotti et al., 1961 |
|
Zanzibar |
1.0E+11 |
11.00 |
8 |
100% |
Reitler et al., 1960 |
|
Enteritidis |
6.0E+00 |
0.77 |
>1 000 |
6% |
Hennessy et al., 1996 |
|
Enteritidis |
2.4E+01 |
1.38 |
>1 000 |
6% |
Vought and Tatini, 1998 |
|
Enteritidis |
1.0E+03 |
3.00 |
39 |
100% |
Levy et al., 1996 |
|
Enteritidis |
1.0E+04 |
4.00 |
39 |
100% |
Levy et al., 1996 |
The dose-response relationship subsequently used was a beta-Poisson model fitted to the human feeding trial data for Shigella dysenteriae M131, with parameters alpha = 0.2767 and beta = 21.159 (www.fsis.usda.gov/OPHS/risk/semodel.htm, July 2000). Uncertainty was introduced into the beta parameter by characterizing it as a normal distribution truncated at zero, with a maximum of 60 and a mean and standard deviation of 21.159 and 20 respectively for the proportion of the population assumed to be in good health (normal subpopulation). In addition, the beta parameter of the S. dysenteriae beta-Poisson model was reduced by a factor of 10, thus shifting the curve to the left to estimate a higher probability of illness for susceptible individuals (susceptible subpopulation). Uncertainty in the beta parameter for the susceptible subpopulation was therefore introduced using a normal distribution with a mean and variance of 2.116 and 2.0 respectively, and a minimum of 0 and maximum of 6.
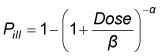
|
Model Used: |
Beta-Poisson |
|
Parameters: |
|
|
Normal |
Alpha = 0.2767 |
|
Susceptible |
Alpha = 0.2767 |
|
Comment: |
Human feeding trial data for Shigella dysenteriae used as a surrogate. Susceptible population characterized by reducing beta parameter by a factor of 10. Simulation of public health outcomes for normal and susceptible subpopulations incorporates the uncertainty represented in the beta parameters. |
Health Canada Salmonella Enteritidis dose-response relationship
The Health Canada Salmonella Enteritidis risk assessment used a re-parameterized Weibull dose-response model. Bayesian methods were employed as a means to provide a consistent framework for combining information from various sources including feeding and epidemiological studies (Health Canada, 2000, but unpublished). The Canadian Salmonella Enteritidis risk assessment had not been published at the time of preparing this report, but a brief description of the procedure used is provided, and the model generated is compared with the other alternatives.
The Canadian model begins with the Weibull dose-response model:
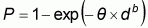
where d is the dose.
The model was re-parameterized as summarized below (Health canada, 2000, but unpublished), and this is the equation that is referred to in the remainder of this section.
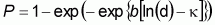
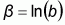
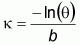
The parameter b in the model was characterized by performing a meta-analysis of all the bacterial feeding trial data. This analysis determined that the log transformed value of b, termed b (b = ln[b]) could be well described using a normal distribution with mean of -1.22 and a standard deviation of 0.025. This characterization of b for all bacterial pathogens represents between-study variability, which is used as a reference input (Health Canada, 2000, but unpublished). Epidemiological data - specifically information generated from the Schwanns ice cream outbreak (Hennessy et al., 1996; Vought and Tatini, 1998) - was incorporated into the model by adjusting the parameter q.
In order to adjust the parameter q, the following equation in terms of epidemiological information was used (Health Canada, 2000, but unpublished):
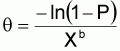
where P represents the attack rate reported in an epidemiological outbreak and X represents the dose estimated to have caused the outbreak.
Within the model, the dose ingested was defined stochastically so as to reflect the uncertainty associated with the data. A single value for the attack rate P was used, and this was estimated to be 6% (Hennessy et al., 1996). The dose was estimated based on the concentration reported and the amount of ice cream consumed. The concentration (in CFU/g) was characterized using a lognormal distribution with a mean of 0.15 and a standard deviation of 0.1. The amount of ice cream consumed was estimated using a PERT distribution with a minimum of 60, a mode of 130, and a maximum of 260.
A separate dose-response relationship was generated for the susceptible population, which was based on epidemiological information. Specifically, information from a waterborne outbreak of S. Typhimurium in Riverside, California (Boring, Martin and Elliott, 1971), which reported on age-specific attack rates, was used to shift the value of q according to the following equation (Health Canada, 2000, but unpublished):
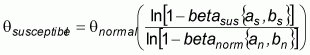
where the parameters (a and b) for the beta distributions are estimated from the reported epidemiological data on the total number of individuals exposed and the number that became ill. The subscripts s and n refer to the data for susceptible and normal populations respectively.
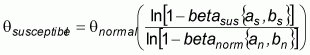
|
Model Used: |
Re-parameterized Weibull |
|
Parameters: |
Beta = Normal (m: -1.22, s:0.025) |
Several parameters in the dose-response models described incorporated uncertainty into their characterization. In order to display the dose-response curves in the following sections, the uncertainty in those parameters has been simulated and the specified moments displayed.
The following abbreviations are introduced and will be used when referring to the dose-response curves: Can-norm = Canadian normal population dose-response; Can-susc = Canadian susceptible population dose-response; US-norm = the United States of America normal population dose-response; US-susc = the United States of America susceptible population dose-response; and Naive-BP = beta-Poisson dose-response curve fitted to naive subject human feeding trial data. These are shown in Figures 3.6 to 3.8.
Figure 3.6. Dose-response curves for normal (Can-norm - upper panel) and susceptible (Can-susc - lower panel) populations, as estimated in Canadian Salmonella Enteritidis risk assessment.
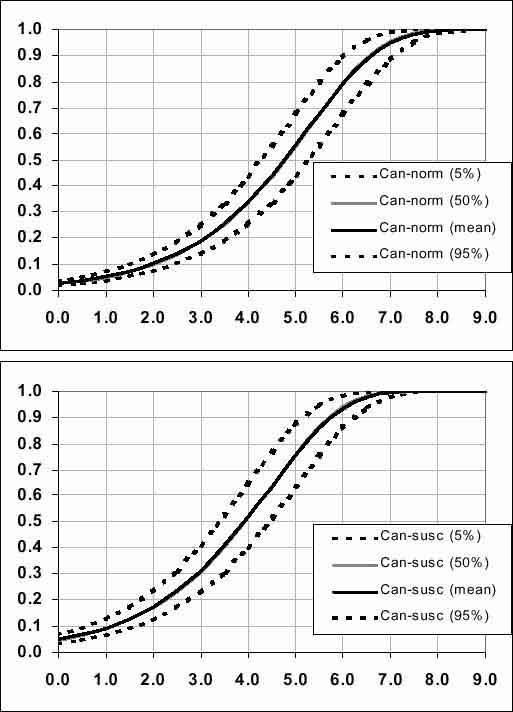
Figure 3.7. Dose-response curves for normal (US-norm - upper panel) and susceptible (US-susc - lower panel) populations, as estimated in the US SE RA.
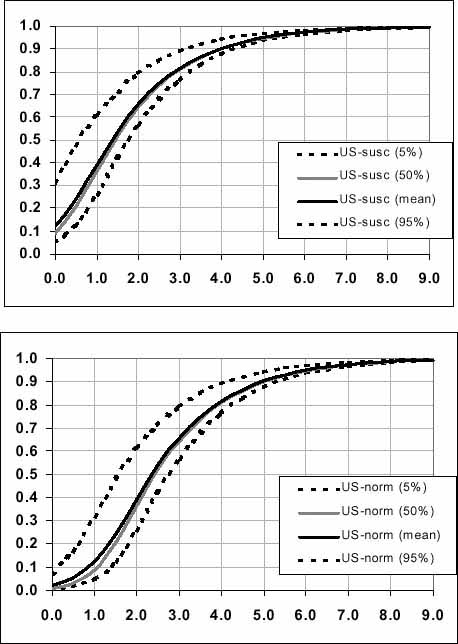
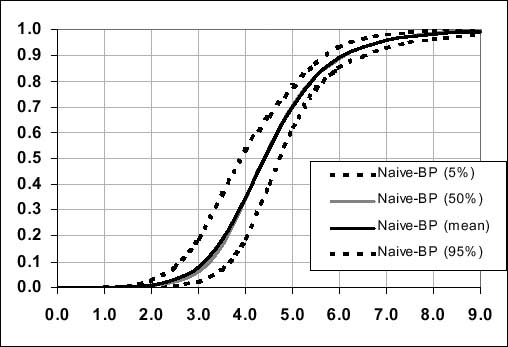
Figure 3.8. Beta-Poisson dose-response curve fitted to naive subject non-typhi Salmonella human feeding trial data (Naive-BP).
The five dose-response curves are plotted together in Figure 3.9 to assist in the comparison of the curves. Since the 50th percentile and the mean are very similar in all five dose-response curves (Figures 3.6 to 3.8), only the mean values for the curves are plotted. The 95th percentile and 5th percentile boundaries for the curves are omitted from this figure for visual reasons.
Figure 3.9. Comparison between five dose-response curves: Can-norm, Can-susc, US-norm, US-susc and Naive-BP.
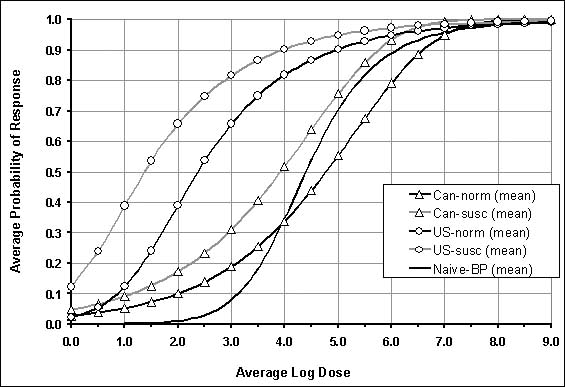
There is some overlap between the Can-norm and the Naive-BP dose-response curves. However, the Naive-BP curve estimates a higher probability of response than the Can-norm for individuals exposed to a dose greater than approximately 104 cells. At an average dose of less than approximately 104 cells, the Can-norm dose-response curve estimates a greater probability of response than does the Naive-BP. In fact, at an average dose of 2 log (100 cells) the Can-norm dose-response curve estimates a probability of response of approximately 10% compared with approximately 1% for the Naive-BP dose-response curve. The adjustment of the Canadian dose-response curve to reflect epidemiological information, specifically the 6% response rate at a dose of approximately 1 log (Hennessy et al., 1996; Vought and Tatini, 1998) is evident in the behaviour of the curve in that lower-dose region.
The US-norm and US-susc dose-response curves, which are based on using Shigella as a surrogate pathogen, estimate a higher probability of illness at a given dose than the other dose-response curves across almost the entire dose range, except the lowest (£10 organisms). At the 2 log (100 cells) average dose level, the normal population using the United States of America dose-response curve would be estimated to have approximately a 40% average probability of response and the susceptible population would be estimated to have approximately a 65% probability of response. This can be compared with 10% and 18% for normal and susceptible populations using the Canadian dose-response curves.
The dose-response curves thus have a significant degree of deviation from each other. Selecting a dose-response curve from this information would have to be based on several considerations that include: the level of conservatism that one wishes to employ; the theoretical acceptability of using a surrogate pathogen; the biological plausibility of various functional forms for modelling dose-response relationships; the biological endpoint or public health outcome of interest; or the acceptability of the human feeding trial data in capturing the overall response for a population.
In order to gain additional insight into the pathogenesis of Salmonella, the available data from epidemiological information were explored.