(2.3)
Considerando un modelo que relaciona la característica y con el tiempo t, en el cual la suposición básica es:
, para
Adoptando la condición inicial: para
 ,
,

1. ¿Como llamaremos a este modelo?
Escribir la expresión general para el valor de la característica y en el instante t;
2. Calcular el valor de y cuando t = 0, 1, 2, 3, 4, 5, 6 y dibujar el gráfico de y contra t.
3. Considerando el intervalo de tiempo, Dt, de
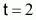 a
a

a) Calcular la variación de y durante el mismo intervalo Dt;
b) Calcular el valor central de y en el intervalo Dt;
c) Calcular el valor acumulado de y en ese intervalo, ycum;
d) Calcular el valor medio,
, de y, en el intervalo Dt;
e) Calcular la media aritmética simple de y en el intervalo Dt;
f) Verificar que la media aritmética de y es igual al valor medio,
, y igual al valor central, ycentral, de y en ese intervalo.
g) Se pretende verificar que en el caso del modelo lineal la tma(y) = tia(y) = constante. Para ello, calcular, para el intervalo Dt antes referido, la tma(y) y la tia(y) y comparar los resultados.
Repetir el ejercicio 3 considerando el intervalo de t = 0 a t = 10.