(7.3)
REVISIÓN DE MATRICES
GRUPO I
Considerando las matrices A y B:
|
A = |
2 3 0 1 |
B = |
1 1 0 3 |
|
|
1 1 4 1 |
|
1 3 2 5 |
|
|
0 4 2 2 |
|
2 1 6 0 |
|
|
1 0 3 3 |
|
2 2 1 0 |
1. Calcular con la ayuda de una hoja de cálculo: A + B, A * B, Det(A), Det(B), A-1 y B-1
2. Demostrar que (A.B)-1 = B-1.A-1
3. Demostrar que (A.B)T = BT.AT
GRUPO II
Sean las Matrices:
|
M(4,4)= (1/4) |
1 1 1 1 |
O(4,4) = |
0 0 0 0 |
I(4,4) = |
1 0 0 0 |
|
|
1 1 1 1 |
|
0 0 0 0 |
|
0 1 0 0 |
|
|
1 1 1 1 |
|
0 0 0 0 |
|
0 0 1 0 |
|
|
1 1 1 1 |
|
0 0 0 0 |
|
0 0 0 1 |
1. Verificar que la matriz nula 0 es ídempotente.
2. Verificar que la matriz identidad I es ídempotente.
3. Verificar que la matriz M es ídem potente.
4. ¿Cual es la traza de M y de I?
5. Calcular la característica, r, de M y de I.
6. ¿Cual es el valor del determinante de M y de I.?
GRUPO III
1. Verificar que el producto Mx, donde x es el vector dado por
 es el vector de dimensiones
(4,1) en que todos los elementos son iguales a la media aritmética,
es el vector de dimensiones
(4,1) en que todos los elementos son iguales a la media aritmética,
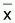 , de los 4 elementos del
vector x.
, de los 4 elementos del
vector x.
2. Verificar que (I-M)x es el vector de las desvíaciones.
3. Verificar que la suma de los cuadrados de xi,
S(xi2) se puede escribir en
la forma matricial:  .
x
.
x
4. Verificar que la suma de los cuadrados de las
desvíaciones, S(xi -
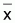 )
)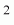 ,
también se puede escribir en la forma matricial como:
,
también se puede escribir en la forma matricial como:

GRUPO IV
Considérese el vector x = 2 + q donde q es un parámetro desconocido.
a) Escribir el vector derivada
b) Calcular
c) Calcular
(
)
d) Demostrar que
2. Considerando el vector x = 2 + 4q1 - 5q2 donde q1 y q2 son dos constantes.
1 + q1 + q2
q1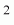 +4q2
+4q2
a) Escribir la matriz derivada
b) Calcular
c) Calcular la matriz transpuesta de
d) Demostrar que la transpuesta de
GRUPO V
Considerando el siguiente sistema de 2 ecuaciones de 2 incógnitas
5 = 2 A + 3 B
4 = A - 2 B
1. Demostrar que el sistema de ecuaciones se puede escribir en la forma matricial
Y(2,1) = X(2,2) q(2,1)
donde Y es el vector de los términos independientes (5 y 4) del sistema,
q el vector de las incógnitas (A y B)
y X la matriz de los coeficientes de las incógnitas
2. Verificar que la solución del sistema puede venir dada por q = (XTX)-1XTY
3. Demostrar que X es una matriz cuadrada no singular y que, por lo tanto, la solución del sistema puede ser q = X-1Y
ESTIMACIÓN DE LOS PARÁMETROS DEL MODELO DE YOSHIMOTO Y CLARKE
(1993)
4. Estimar los parámetros k, q y r, del modelo integrado de Fox (IFOX) de Yoshimoto y Clarke (1993) usando los siguientes datos:
|
Año |
Y |
CPUE |
|
1983 |
538 |
235 |
|
1984 |
638 |
131 |
|
1985 |
431 |
63 |
|
1986 |
99 |
22 |
|
1987 |
37 |
8 |
|
1988 |
62 |
21 |
|
1989 |
437 |
77 |
|
1990 |
146 |
28 |
|
1991 |
126 |
26 |
|
1992 |
53 |
25 |
|
1993 |
91 |
41 |
|
1994 |
232 |
66 |
que representan las capturas totales anuales (en toneladas) y las respectivas capturas por unidad de esfuerzo de pesca (kg/día de pesca de la empresa PESCRUL) del stock de gamba Parapenaeus longirostris del Algarve, durante el período 1983 a 1994 (Mattos Silva, 1995).
Comentar los resultados obtenidos comparándolos con los presentados en la Sección 8.20.