K.D. Singh
K.D. Singh, of the Indian Forest Service, is a specialist in forest inventory and data processing.
The author gives a detailed analysis of three kinds of patterns of spatial variation in surveys of tropical rain forests. They indicate that what seems to be a bewildering chaos of vegetation does in fact have an organized structure. He suggests the technical and economic practicality of making surveys of tropical rain forests on the species group level.
In this article some common patterns of variation observed in rain forests are described, mainly based on existing knowledge, but also adding some unpublished material. First, macropatterns are discussed, indicating their significance for stratification, then micropatterns and their importance for the choice of size and shape of the sampling unit, and, finally, variation patterns at an intermediate scale and their role in the choice of sampling scheme, i.e., clustered vs nonclustered, random vs systematic layouts.
The tropical rain forest is natural climax vegetation of the equatorial belt. Climatic factors essential for its development are a uniformly high temperature (about 24-26°C) and a long wet season of 10-12 months.
Main areas of tropical rain forest are:
South and Central America - The Amazon basin (Brazil), extending west to the lower slopes of the Andes, east to the Guianas, south to the Gran Chaco and north along the eastern side of Central America.Africa - The Congo basin (mainly Zaire and Congo), Gabon and Cameroon. It extends westward into Nigeria, Ghana, Ivory Coast, Liberia and Guinea. On the eastern side it extends to Uganda.
Asia - Mainly in southeast Asia, including the Malay peninsula, the islands of Sumatra, Borneo, Celebes and New Guinea. It also occurs partly in India, Sri Lanka, Burma, Thailand and the Philippines.
Although tropical rain forest occurs in widely separated areas, ecological studies show evidences of striking similarities among the formations. According to Richards (1971) they are composed of similar synusiae or communities of trees with homogeneous characteristics and show great similarity in their spatial arrangement. Species of corresponding synusiae in different geographical regions, as well as being alike in life-form, are to a considerable extent alike in physiognomy. The fundamental pattern of structure is thus the same through the whole extent of the rain forest.
These findings suggest that it would be interesting to investigate common patterns of variation which may be meaningful from the point of view of inventory design. It is obvious that such knowledge could facilitate exchange of inventory information among the regions, and add to the efficiency of survey designs.
For planning an inventory, variation patterns at many scales are of interest. For decisions regarding stratification, macropatterns are sought, e.g., changes in land use, forest type and logging class. For choice of size and shape of the sampling unit, the microvariation is more critical. For selection of a sampling scheme some knowledge of the variation pattern at the intermediate scale is required.
The following sections present a brief review of variation patterns at three scales.
Causes for differentiation within the rain forest formation can be divided into two broad groups, natural and cultural.
Among the natural factors climate is relatively uniform. Soil and topography appear as the main agents for causing variation. Some common types are:
- Climax rain forest (usually on well-drained soils and below elevations of 500-800 m).
- Mangrove forest.
- Swamp forest.
- Periodically flooded forest.
- Riparian forest.
- Hill forest (usually at altitudes above 500-800 m).
- Forest on tropical podsols.
- Forest on coastal sand.
Cultural factors (positive or negative influence of man) cause further changes in the natural rain forest vegetation. The following broad types can be distinguished:
- Primary rain forest (influenced less by man).
- Logged-over forest.
- Secondary forest (resulting from abandoned shifting cultivation).
- Mixed forest-grassland association.
- Managed forest (natural and manmade).
- Other nonforest land-use classes.
There are distinct differences among the above types in respect to species, number of stems per area unit, storeys and volume per area unit. It may also be observed that the more conditions become limiting for growth, the more there is a tendency toward uniformity.
Existing studies show that it is possible to identify most of the macropatterns, of both natural and manmade forests, with conventional aerial photographs at a scale of 1:20 000 or less.
Since the primary rain forest occupies a relatively large area compared to other types, several investigations have been made to explore the possibilities of further stratification. A review of these are given by Nyyssönen (1961) and Loetsch et al. (1973). It appears rather difficult to distinguish further ecological types with the help of aerial photographs because vegetation cover in the rain forest looks very uniform, extending over large territories without any changes or border lines.
On the other hand, it has been found possible to delineate broad volume/basal area classes, utilizing correlation between crown density of dominant trees and gross volume per area unit of all species. A pilot analysis carried out by the author on a survey in Laos in 1969, based on data from 185 plots, showed the value of the square of multiple correlation coefficient (R²) to be 0.64. A close relation was also observed in an FAO survey of the Amazon valley.
A broad density classification has been used by several inventories in Asia, Africa and Latin America. The gains in precision reported by an FAO survey in Sarawak are shown in Table 1.
1. NINE-POINT CLUSTER, SARAWAK SURVEY
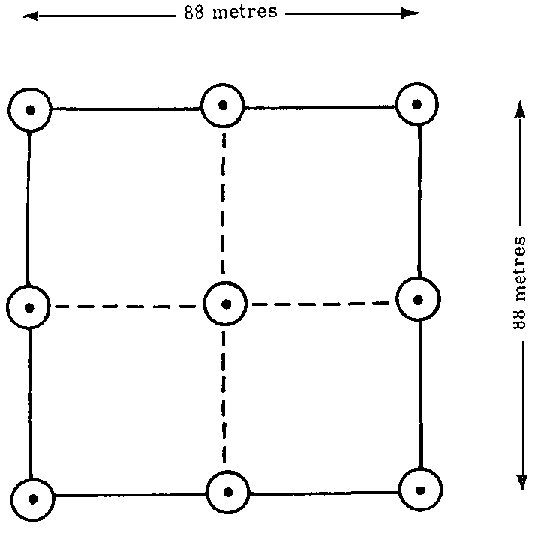
Mesovariation pattern, i.e., the variation between macro and micro levels, is a relative concept which depends on the survey area as well as on the size and shape of the sampling unit. The object is to study the variations between sampling units.
In the early stages of the Sarawak forest inventory an analysis of variance was carried out to discover the relative component of variation within and among samples to determine the optimum number of plots in the cluster. Data from two units (l and 3) were available, covering an area of 176 000 and 225 000 ha respectively. The sampling unit consisted of a nine-point cluster, as shown in Figure 1.
A tally was taken with a relaskop of BAF 10 sq ft/acre (2.3 sq m/ha). There were 50-100 such samples uniformly spread over the two survey units. Results are given in Table 2.
The value of R², computed as s b²/(s b²+s w²), was found to be 0.3, showing relatively low variation between samples compared to the variations within a sample. A similar high variation within individual sampling units was also observed by the author's analysis of FAO's survey data of peninsular Malaysia.
For the rain forest of the Amazon valley, Ramos et al. (1972) found the value of R² to be 0.3 in one case and 0.5 in another. The sampling unit consisted of four closely spaced rectangles of 250 x 10 m located 10 m from the cluster centre and pointing in all four directions.
An analysis at the level of species groups (31 groups in all) for the Sarawak forests (unit 2) showed much lower intraclass correlation of the order of 0.2 and less for all the groups except one, a nondipterocarp species group where R² was found to be 0.5.
Boon (1962) studied the variation pattern of Eusideroxylon zwageri by dividing the survey area into blocks of variable sizes, 2 x 1, 4 x 1 and 4 x 2 km. Each block was further split into two sub-blocks to compare the variance among and within the blocks. Analysis showed that variance between the blocks was not significantly different from that within blocks. This was observed for all the blocks and all the plot sizes.
TABLE 1. - GAINS FROM STRATIFICATION¹
|
Sampling scheme |
Precision estimates for the survey regions (±) |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
Percent |
||||||||
|
Unstratified |
6.7 |
8.1 |
9.6 |
6.6 |
7.2 |
7.9 |
10.4 |
10.0 |
|
Stratified (post) |
4.5 |
6.8 |
7.6 |
4.0 |
3.7 |
4.2 |
5.4 |
5.6 |
¹Character: Precision estimate for the parameter net industrial volume of all species 18 in (45 cm) and more in diameter (95 percent confidence level).
TABLE 2. - ANALYSTS OF VARIANCE FOR THE CHARACTER GROSS
VOLUME/ACRE ¹ OF ALL SPECIES 18 TN (45 cm) AND MORE IN DIAMETER (UNIT 1)
|
Source of variation |
Degrees of freedom |
Sum of squares |
Mean sum of squares |
Variance components |
|
Among samples |
81 |
431448800 |
5326528.3 |
s b² = 474223.86 |
|
Within samples |
656 |
694383300 |
1058511.1 |
s b² = 1058511.10 |
¹ Mean: 2031 ft³/acre (142 m³/ha).
TABLE 3. - EFFECT OF SIZE AND SHAPE OF PLOT ON COEFFICIENT OF VARIATION OF TOTAL VOLUME OF ALL SPECIES
|
Forest type |
Mean volume |
Estimated coefficient of variation |
Number of samples |
|||
|
Square plot |
Rectangular plot |
|||||
|
03 ha |
0.6 ha |
0.3 ha |
0.6 ha |
|||
|
m³/ha |
Percent |
|||||
|
Rain forest |
393 |
98 |
82 |
75 |
48 |
14 |
|
Moist deciduous |
177 |
63 |
60 |
60 |
58 |
25 |
Source: FAO report, Forest resource survey. India. 1970.
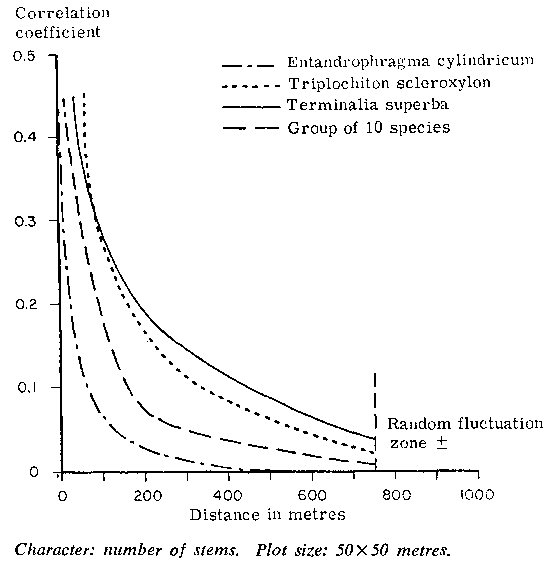
Giudicelli et al. (1972) studied the spatial correlation for the number of stems for three important species and one species group in a forest area of 1 500 ha in Cameroon, using a plot 50 x 50 m. The "correlogram" observed by them is given in Figure 2. It shows high variability within small distances in respect of all the species. Furthermore, the correlogram shows concavity toward the origin. In such cases systematic sampling is expected to be more efficient than random sampling.
The above results clearly show an important feature of the rain forest: high variability within small areas and relative uniformity over large areas. This indicates that the use of some type of cluster sampling will not result in much loss of precision.
The complexity of the microvariation, which an inventory has to sample, depends to a great extent on the objective in species separation. If parameters are to be estimated only at the level of all species, the variation pattern is relatively simple.
To study the influence of the size and shape of the sampling unit on precision, a pilot survey was carried out in India. There were 39 samples in all spread over two forest types, covering an area of about 80 000 ha. Results showed that in the rain forest both size and shape had important influences on the coefficient of variation. On the other hand, in the adjoining moist deciduous forest, size and shape had little effect on precision, as shown in Table 3.
Survey experiments carried out in the rain forest of Indonesia, with 20-m wide rectangular plots of variable length, showed that coefficient of variation decreased exponentially with increase of the plot size. It tended to approach a stabilized value of 16 percent beyond a size of 1.5 ha (see Nyyssönen, 1961).
At species level, spatial arrangement in the rain forest becomes very complicated. As Richards phrased it, it appears at first to be a bewildering chaos of vegetation. Detailed investigations carried out by several ecologists, however, show that the rain forest, like any other ecological community, has an organized structure. Constituent plants form a limited number of synusiae with a discernible, though complicated, arrangement in space. This arrangement is repeated as a pattern with only a small amount of variation throughout the rain forest formation (Richards, 1971).
Heinsdijk (1961) investigated the spatial arrangement of species in the Amazon valley. He found that the distribution of many species approached a Poisson distribution pattern but there were often exceptions where sampling units showed a high number of particular species, indicating a tendency toward contagious distribution.
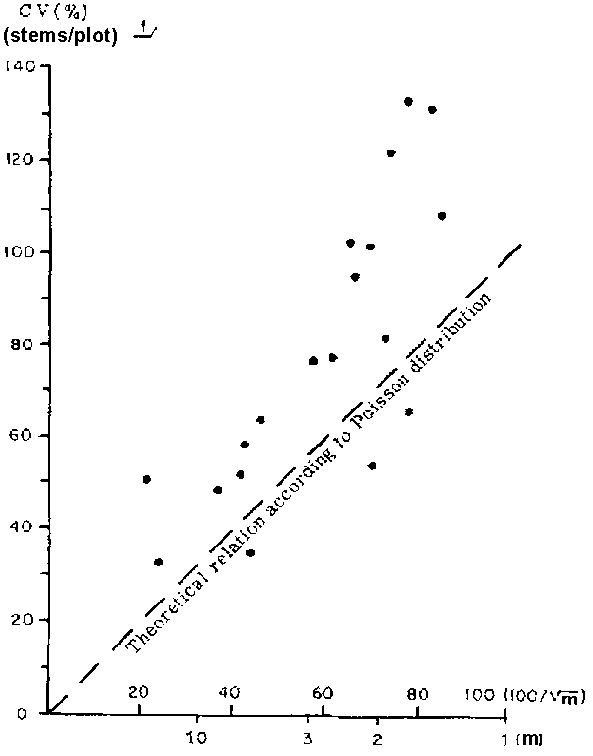
Utilizing the survey data from the Amazon valley, Surinam and Sarawak, the author carried out a series of investigations. For the most important 10-20 species, the mean number of stems per sampling unit (m) and its coefficient of variation (cv) were plotted, and the relationship between two parameters was studied.
2. CORRELOGRAM FOR THREE SPECIES AND ONE GROUP OF TEN SPECIES OF THE SEMIEVERGREEN FOREST IN CAMEROON
For a strict Poisson distribution the points relating 100/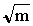 and cv should fall on a straight line inclined 45° to the X-axis. This is because of an important feature of a Poisson distribution which is mean equals variance. In all cases (see Fig. 3) the species tended to deviate upward from the expected straight line relation, indicating grouping tendencies. It is clear that in such cases the expression 100/
and cv should fall on a straight line inclined 45° to the X-axis. This is because of an important feature of a Poisson distribution which is mean equals variance. In all cases (see Fig. 3) the species tended to deviate upward from the expected straight line relation, indicating grouping tendencies. It is clear that in such cases the expression 100/ is not a very satisfactory guide for estimating the coefficient of variation.
is not a very satisfactory guide for estimating the coefficient of variation.
Investigations of Boon (1962) for Eusideroxylon zwageri show that this species has a marked grouping tendency.
Jack (1961) studied the spatial arrangement of the seven most important commercial species of the semievergreen forest of Ghana, using sampling units of various sizes and shapes. For Triplochiton scleroxylon, Khaya ivorensis and Entandrophragma cylindricum he found a significant departure from the Poisson distribution and a good fit with negative binomial distribution. Entandrophragma utile and Mimusops heckelli showed grouping be observed only with plot sizes larger than 2.0 ha, whereas Chlorophora excelsa, with change of plot sizes, exhibited a vacillating pattern between random and contagious.
Giudicelli et al. (1972), in a similar type of forest in Cameroon, observed a pronounced contagious distribution for Triplochiton scleroxylon and Terminalia superba but an approximately random distribution in the case of Entandrophragma cylindricum. They also found that the distribution pattern, when 10 important species were grouped together, tended to become regular.
Studies of non-Poisson distributions are complicated by the fact that the pattern, as revealed from the observed data, is confounded partly with the size and shape of the plot. According to Greig-Smith (1964), many types of nonrandom patterns appear random when sampled by very small or large plots, but are nonrandom with intermediate sizes. This shows the need for caution in drawing general conclusion patterns of species. The above consideration, together with ecological studies quoted earlier, clearly indicates, however, that within the range of plot sizes used many dominant species of the rain forest show a contagious distribution.
An inventory man is not so much interested in the patterns as such as he is in their implications for the survey design. For pure randomly distributed populations (viz. Poisson) the planning job is rather simple. Here, precision of estimate depends only on the number of individuals counted. The standard error of estimate will be the same whether many small plots or few large ones or even a single big plot are used (Greig-Smith, 1964). The shape of the plot has no effect. Similarly, survey precision will hardly be affected if plots are randomly or systematically arranged, or if they are clustered or not clustered.
The situation is complicated for contagious distributions. One consequence has already been mentioned: lack of definite correlation between the plant density and coefficient of variation. Secondly, both the size and the shape of the sampling unit influence the precision of estimates. It is commonly observed that for the same sampling intensity small but well-dispersed plots give a higher precision than a few compact big plots (Dawkins, 1952; Lanly and Vannière, 1969; Greig-Smith, 1964).
Species differ in their response to the increase of the plot size. Their differential behaviour can be correlated with their spatial arrangement. Triplochiton and Terminalia, both of which have marked contagious distribution, show, relatively speaking, more loss of precision with the increase of plot size than Entandrophragma utile, whose spatial arrangement approximates Poisson distribution (see Fig. 2). Eusideroxylon zwageri and Khaya ivorensis, both of which also show aggregation tendency, behave in a similar way.
3. RELATION BETWEEN COEFFICIENT OF VARIATION (CV) AND 100/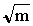
In the case of contagious distribution, elongated sampling units result in more precise estimates than compact units of the same size. This fact can be easily visualized: the former is more likely to fall in both dense and rare patches than the latter.
Investigations by Jack (1961) show that long and narrow sampling units with general orientation across local drainage give more precise results than relatively compact ones. Similar experiences with ecological studies have also been reported by many investigators, e.g., Greig-Smith (1964, p. 29) and Aubréville (1971).
So far attention has been confined to the study of contagious distributions only, because of their wide occurence in the rain forests. There are many other possibilities in which plants can be arranged in space. One example is the "regular distribution" mentioned earlier in connexion with the distribution of "groups of 10 species." In the light of the above studies it would appear that an inventory in the rain forest at the level of individual species would be very expensive compared to that for "all species." As an alternative, it would be interesting to know what happens at the species group level. An expected effect of species grouping is a decrease in the coefficient of variation.
Mean and coefficient of variation for various species and levels of species grouping for the mixed dipterocarp forests of Sarawak are presented in Table 4.
They clearly show that economy in sampling is achieved by working at the level of species groups. Compared to the individual species, at group level there is much less variability. The number of blank sampling units declines and the asymmetry in the frequency curve decreases. The effect of the size and the shape of the sampling unit is still marked and, as mentioned earlier, it continues to be so even at the "all species level."
TABLE 4. - MEAN AND COEFFICIENT OF VARIATION OF BASAL AREA/HA AT GROUPS AND SPECIES LEVEL FOR TREES 18 IN (45 cm) AND MORE IN DIAMETER (83 SAMPLES, UNIT 1)
|
Groups/species |
Mean basal area |
Coefficient of variation |
|
m²/ha |
Percent |
|
|
All species |
14.70 |
27 |
|
Dipterocarps |
9.89 |
32 |
|
Red merantis |
4.10 |
40 |
|
Shorea parvifolia |
2.46 |
111 |
|
Shorea sagittata |
1.52 |
122 |
|
Shorea rubra |
0.95 |
142 |
|
Shorea macroptera |
0.35 |
187 |
|
Yellow merantis |
1.28 |
85 |
|
Shorea collards |
1.14 |
234 |
|
Kapurs |
1.21 |
141 |
|
Dryobalanops oblongifolia |
2.37 |
202 |
|
Dryobalanops aromatica |
1.59 |
191 |
|
Keruings |
1.16 |
82 |
|
Dipterocarpus pachyphyllus |
0.086 |
270 |
|
Nondipterocarps |
4.68 |
39 |
|
Light-density species |
2.12 |
50 |
|
Medium-density species |
1.23 |
67 |
|
Heavy species |
0.93 |
68 |
SOURCE: FAO report, A description of the data processing system...Malaysia. 1973.
AUBRÉVILLE, A. 1971. Regeneration patterns in the closed forests of Ivory Coast. In World vegetation types, ed. by S.R. Eyre, p. 41. London, Macmillan.
BOON, D.A. 1962. Plot size and variability. Delft, International Training Centre for Aerial Survey. ITC Publication, Series B. No. 17.
Cox, F. 1971. Dichtebestimmung und Struktur-analyse von Pflanzenpopulationen mit Hilfe von Abstandsmessungen. Mitt. BundForsch-Anst. Forst- u. Holzw., 87.
DAWKINS, H.C. 1952. Experiments in low percentage enumerations of tropical high forest with special reference to Uganda. Emp. for. Rev., 31:131.
DAWKINS, H.C. 1958. The management of natural tropical high forest with special reference to Uganda. Oxford, Imperial Forestry Institute Paper No. 34.
GIUDICELLI, X., LANLY, J.P., OUAKAM, J.B. & PIETRY, M. 1972. Application de la théorie des processus aléatoires a l'estimation de la précision d'un inventaire forestier par échantillonnage systématique. Annls sci. for., 30:267.
GREIG-SMITH, P.1964. Quantitative plant ecology. London, Butterworths.
HEINSDIJK, D. 1961. Forest survey in the Amazon valley. Unasylva, 15:167.
JACK, W.H. 1961. The spatial distribution of tree stems in a tropical high forest. Emp. for. Rev., 40:234.
KEMPTHORNE, O.1957. An introduction to genetic statistics. New York, Wiley.
LANLY, J.P. & VANNIÈRE, B. 1969. Precision d'un inventaire forestier en fonction de certaines de ses caractéristiques. Bois Forêts Trop., No. 125:35.
LOETSCH, F. & HALLER, K.E. 1973. Forest inventory. Vol. 1. München, BLV Verlagsgesellschaft.
LOETSCH, F., ZÖHRER F. & HAILER, K.E. 1973. Forest inventory. Vol. 2. München BLV Verlagsgesellschaft.
MATÉRN, B. 1960. Spatial variation. Meddn St. SkagsforskInst., 49(5).
MATÉRN, B. 1972. Poisson process in the plane and related models for clumping and heterogeneity. Symposium lecture on Analysis of spatial patterns and ecological relations.
MEYER, H.A. 1953. Forest mensuration. State College, Pa.
NYYSSÖNEN, A. 1961. Survey methods of tropical forests. Rome, FAO.
RAMOS, A.A., VIEIRA, A.N., VIVACQUA, C.A., ALENCAR, J.C, BARROS, J.C.M. & PÉLLICO NETTO, S. 1972. Inventario florestal do distrito agropecuario da zona Franca De Manus. Revta flor., 4(1).
RICHARDS, P.W. 1952. The tropical rain forest, p. 10, 249. Cambridge, University Press.
RICHARDS, P.W. 1971. The structure of tropical rain forest. In World vegetation types, ed. by S.R. Eyre, p. 26. London, Macmillan.
SCHIMPER, A.F.W. 1903. Plant-geography upon a physiological basis. Tr. by W.R. Fischer. Ed. by P. Groom and I.B. Balfour. Oxford, Clarendon Press.
WECK, J. & WIEBECKE, C. 1961. Weltforstwirtschaft and Deutschlands Forst- und Holzwirtschaft. München
BRAZIL
1957. Report to the Government of Brazil on the forest inventory in the Amazon valley. FAO/ETAP Report No. 601.
1965. Report to the Government of Brazil on forest inventories in the Amazon. FAO/ EPTA Report No. 2080.
GUYANA
1970. Inventory of the Ebini-ltaki area. Guyana. Forest Industries Development Survey. Technical Report No. 9. FO-UNDP/SF GUY/9.
INDIA
1970. Forest resource survey. India. Preinvestment Survey of Forest Resources. Technical Report No. 1. FO-UNDP/SF IND/23.
MALAYSIA
1973. A description of the data processing system used in the inventory of selected areas of the mixed dipterocarp forest in Sarawak. Malaysia. Forestry and Forest Industries Development Project. Working Paper No. 22. FO:DP/MAL/72/009.
1973 The timber species of the mixed dipterocarp forest of Sarawak and their distribution. Malaysia. Forestry and Forest Industries Development Project. Working Paper No. 21. FO: DP/MAL/72/009.