Papers presented at the workshop

Fishery statistics

Review of fishery statistics collected by FAO in the asian region

Luca Garibaldi
Fishery Information, Data and Statistics Unit
FAO Fisheries Department, Rome

This paper intends to provide background information on the capture fishery statistics included in the FAO database to the Workshop's participants. The FAO fishery statistics programme is briefly introduced. The FAO Fishery Information, Data and Statistics Unit (FIDI) collates annual global fishery statistics on capture and aquaculture production, trade, apparent consumption, fishing vessels and fishers. Capture statistics are collected through national correspondents by country, FAO fishing area and species. The quality of the FAO statistics is dependent upon the accuracy and reliability of the statistics collected nationally and provided to FAO. The yearly steps from the dispatch of questionnaires to data dissemination are as follows:

• dispatch of printed and electronic questionnaires (NS1 for capture statistics);

• follow-up with countries which do not return data;

• quality control (e.g. species identification, anomalous trends, etc.), validation of data returned and estimation of missing data;

• research and use of complementary sources (e.g. Tuna Commission, National Yearbooks, etc.);

• input of data in the FAO capture databases; and

• data dissemination in electronic (FISHSTAT+) and printed (Yearbooks) versions.

FIDI is also responsible for the: a) harmonization of concepts, classifications and techniques for data collection, processing and dissemination; b) analysis of global and regional trends in periodical (e.g. the State of World Fisheries and Aquaculture (SOFIA)) and special publications; c) secretariat of the Coordinating Working Party on Fishery Statistics (CWP); and d) promotion of the improvement of statistical methodologies.

FIDI is aware of the major problems encountered by many countries in the collection of fishery statistics, e.g. inadequate resources, lack of skilled personnel to collect and compile statistics, non-sustainability of development efforts. In particular, data collection on small-scale fisheries needs improvements, although it may be a very difficult task in some countries with thousands of remote landing places. Statistics from industrial fisheries and for valuable species (e.g. tunas) are more easily available also thanks to the work of regional commissions (e.g. the Indian Ocean Tuna Commission (IOTC) and the Secretariat of the Pacific Community (SPC)). In the last decades the political inclination of reporting continuously increasing trends has been noted in some countries. This seriously affects the capacity at the national level of planning effective fishery management and influences the global trends and the perception of the status of world fisheries.

An analysis of the capture fishery statistics of the Asian countries as a whole, showed that catches have tripled in the last 30 years (from 5.5 million tons in 1970 to 15.7 million tons in 2000) with an average yearly rate increase of 3.5 percent. However, several countries report fishery statistics with no or very low breakdown by species. These statistical data do not provide usable information for the purposes of fishery management or assessment of marine resources.

A simple review of marine catch statistics, including charts with the 1970-2000 trends of marine capture production by major ISSCAAP groups, information on the species breakdown (number of items at the species and higher levels; percentage of "Marine fishes not identified" on the total of the last three years), and brief comments (e.g. species breakdown, data collection system, trends by group, etc.) or information on recent developments for each of the thirteen participating countries are presented below.

Note on FAO activities related to fishery statistical development

Luca Garibaldi
Fishery Information, Data and Statistics Unit
FAO Fisheries Department, Rome

Some of the FAO main activities related to fishery statistics development, namely "ARTFISH", "Guidelines for the collection of capture fishery data", "Western Central Pacific species identification guide" and "ASFIS list of species for fishery statistics purposes", are presented.

ARTFISH is a suite of standardized statistical approaches and computer software developed by FAO-FIDI that assists in the design and implementation of sample-based fishery surveys. It can handle different types of fisheries and has been developed as a decentralized system allowing local processing as well as centralized data integration. The main ARTFISH components are three modules (i.e. ARTPLAN, ARTBASIC and ARTSER) which, respectively, allow training and survey planning, sampling and estimations, reports and graphics. ARTFISH, which has already been implemented in several African countries, should not be regarded only as a computer software but as an all-embracing approach to the collection of fishery statistics. However, a country interested in its running should consider all aspects (e.g. allocation of funds, trained personnel, maintenance of the system, etc.) needed for its implementation at the national level. FAO does not distribute the software if these conditions are not met.

The "Guidelines for the routine collection of capture fishery data" were prepared during a FAO/DANIDA Expert consultation held in Bangkok, Thailand, 18-30 May 1998, and aim to help those who design and implement routine data collection programmes. This document covers all aspects of the collection of fishery data from the indicators and variables to be selected to the strategy and methods of the data collection. Suggestions on the surveys' planning and implementation and on the data management are also provided.

The correct identification of the species caught is the first step for the collection of sound fishery statistics. The FAO Species Identification and Data Programme (SIDP) promotes the upgrading of fisheries data by species through reliable identification publishing species identification sheets and field guides since the early 1970s. For the area of interest of this Workshop, the SIDP has recently completed the publication of a six-volume field guide covering the Western Central Pacific, the world oceans' area with the richest biodiversity.

The "ASFIS list of species for fishery statistical purposes" lists over 10,000 species items including codes and names to facilitate and standardize returns and exchanges of fishery statistics data. It can be easily downloaded from the FAO web site and imported in any database or spreadsheet; a hard copy of the ASFIS list will be available within a few months.

FAO contacts for the above mentioned activities are provided below.

For ARTFISH:

E-mail: [email protected]

To request the Guidelines for collection of fishery data:

E-mail: [email protected]

To request the WCP identification guide:

E-mail: [email protected]

SIDP web site: http://www.fao.org/fi/sidp/default.htm

To download the ASFIS species list:

ASFIS list web site: http://www.fao.org/fi/statist/fisoft/asfis/asfis.asp

E-mail: [email protected]

Fish stock assessment

A short historical review on fish stock assessment in South and Southeast Asia and its relation to the use of statistics

Purwito Martosubroto
Fishery Resources Division
FAO Fisheries Department, Rome

Introduction

The development of the fisheries sector in South and Southeast Asia started to accelerate in the late 1970s and 1980s, when foreign capital started pouring into the region, along with the increased availability of new fishing technology. At the same time the global demand for fisheries products from the tropics also showed an increasing trend, which further augmented the development of the sector. Various forms of technical assistance from developed countries and international organizations (e.g. UNDP) also became available in the 1970s.

The assistance included the assessment of resources; by GTZ for Thailand, Malaysia and later Indonesia; and UNDP for Bangladesh, India, Pakistan and Myanmar; along with others. There were also FAO-executed regional initiatives, including the South China Sea Fisheries Development and Coordinating Programme (SCSP, 1973-1984), the Indian Ocean Programme (IOP, 1973-1978), and the Bay of Bengal Programme (BOBP, 1979-2002). Various training opportunities for national fisheries officers were available through these programmes.

Regional entities

The region, especially countries of Southeast Asia, benefited from the establishment of the Southeast Asian Fisheries Development Center (SEAFDEC) in 1967. It continues to offer training in various disciplines. This includes research related topics, particularly in the fields of post-harvest technology and resources assessment. Substantial facilities are provided at its Training Department in Bangkok.

The region also benefits from the International Center for Living Aquatic Resources Management (ICLARM) now based in Penang, Malaysia. ICLARM has promoted networking amongst tropical fisheries scientists, assisted through FISHBYTE, a special column in its Newsletter, NAGA. In policy matters, the Asia-Pacific Fisheries Commission (APFIC) plays an important role in providing advisory services to countries in the region, both in South and Southeast Asia.

Resource surveys

International initiatives in the area of fisheries resource surveys in the tropical developing countries also started in 1980s. Through financial support from Norway and FAO sponsorship, the R. V. Fridtjov Nansen, was deployed to survey the fish stocks in various waters in the South and Southeast Asia, including the Arabian Sea and adjacent Gulfs (including Pakistan waters), Eastern Indian Ocean (Sri Lanka, Bangladesh, Myanmar, Thailand, Malaysia, and Indonesia) and the South China Sea (Malaysia).

Stock assessment training

In support of the resources surveys, the SCSP and BOBP (to a limited extent) and later FAO/DANIDA, provided training in fish stock assessment specifically relevant to tropical fishery situations. Such trainings were conducted nationally and regionally in South and Southeast Asia, where scientists from fisheries research institutions and to limited extent also from Universities participated. These trainees later became the core staff of many Fisheries Departments in the region.

In the meantime, stock assessment has become one of the important subject-courses offered by some Universities in the region. With the termination of the various FAO-executed programmes, SEAFDEC and ICLARM are the two regional institutions that still conduct training, research, and awareness building relevant to the problems of fisheries in the region.

An interesting development of fish stock assessment in the tropics is in the analysis of fish growth. The difficulty in ageing tropical fish has led scientists to make use of indirect methods such as length-frequency-distribution analysis to come up with growth parameters. With the development of electronic technology, software for length frequency analysis became available (ELEFAN, LFSA, and FISAT).

This led to a great number of papers produced in this regard and resulted in an emerging trend towards dependency by scientists on this methodology. However, caution needs to be exercised since full understanding of the concept of this method is necessary as well as good sampling frame for length measurement needs to be ensured to come up with the right interpretation.

Fishery statistics

The establishment of fisheries catch and effort statistical systems have become important. Through the support of UNDP and other donor agencies, FAO assisted a number of countries to establish their statistical systems in the 1970s and 1980s through the national and regional initiatives such as the SCSP and BOBP. As a result statistics publications have been strengthened, and scientists have started making use of the information from the statistics to better know and understand the status of resources and their exploitation.

Through careful analysis of statistics, scientists can derive indices of fish abundance, such as catch per unit of fishing effort (CPUE). Scientists can also use other measures of abundance from resources surveys. Combining this information with the catch data from the fishery statistics, scientists may apply the various forms of surplus production model, to correlate the relationship between fishing and its impact on the level of annual catches.

In an attempt to improve the quality of statistics, SEAFDEC tried for several years to promote the collection of fishing effort data in Southeast Asia, but with little success. Similar effort was made by the Indian Ocean Tuna Commission (IOTC), by working together with scientists in its member countries to promote the collection of landings and other data at the fishing ports, in order to assess the status of tuna fishing in the region.

Acoustic surveys

In the case of assessment of small pelagic fishes, some scientists have used results from acoustic surveys, in an attempt to determine with the distribution patterns of shoaling fish populations and to estimate their biomass. In many cases, the absence of fishing to obtain sample of fish forming the biomass during the acoustic surveys has been the main constraints, therefore the resources forming the biomass remains unidentified as to whether they are commercially important or not. As a recent initiative, SEAFDEC conducted a series of small pelagic fish survey in the South China Sea using acoustic techniques, and the report of findings is now available.

Ecosystem models

As fishing has impact on the aquatic ecosystem where fish live, various ecological models have been developed and ECOPATH, one of the models that has been applied in various fisheries in the world. The model was recently expanded by a group of scientists in the University of British Columbia (Canada), taking into account temporal and spatial factors (ECOSIM and ECOSPACE) Some pioneering works in the application of the ECOPATH to tropical fisheries in the region have started recently for the southwest coast of India and the Gulf of Thailand and are reported elsewhere in this document.

Concluding comments

The linkage between fishery statistics, stock assessment and management cannot be over-emphasised. Good information provides the basis for stock assessment, while the outcomes from assessments serve as the basis for management action. It will be important that managers enact strategies that ensure the provision of good information from the fishing industry. For example, a condition for issuance/renewal of a fishing licence should be the provision of catch information by the license holders.

The close link between statistics, stock assessment and management demands a strong cooperation between those responsible for statistics collection, research scientists and fisheries managers. Governments can ensure that this occurs, by formally defining the linkages and functions through management plans, and other co-management arrangements. In the absence of such good cooperation, one can only expect continuing financial waste in government spending in the management of the sector.

The common question that always arises in relation to fishery statistics is whether or not the information from the statistics is useful for stock assessment. To answer this question, one should start making use of the statistics for fishery assessment and management purposes. Otherwise, one would not know whether the information is valuable or far from expectation. In the event that the statistics are found to be insufficient, corrective action can then be taken to improve their quality.

Thompson and Bell's yield analysis using Excel spreadsheets

Michael Sanders
Fishery Consultant
Melbourne, Australia

Introduction

This paper was written as an adjunct to demonstrating the Thompson and Bell's approach to assessing fishery performance. Also demonstrated were some of the useful features of Microsoft Excel. The first section deals with important stock assessment relationships and concepts. Reference is then made to an example spreadsheet depicting a length-based Thompson and Bell's model. This was formulated in respect to a multi-gear fishery on a small pelagic species. The final section gives a brief introduction to the Excel features Solver, Data Table, and Macro.

Underlying relationships and concepts

Fishing mortality and fishing effort

Underlying much of assessment work in fisheries is the proportional relationship between fishing effort (X) and fishing mortality (F). The relationship is F = q. X where q is the constant of proportionality and otherwise called the catchability coefficient.

Fishing mortality is the fraction of the fish caught in the time (and space) interval under consideration. The associated equation is F = C_n/N' where C_n is the catch number and N' is the mean stock number.

Combining the above two equations gives C_n/X = q.N'. The left-hand side is catch per unit effort (CPUE). This relationship between CPUE and mean stock number is another of the basic relationships.

Where the fish are uniformly distributed and redistribution occurs between each unit of effort, then the fraction of the fish caught is the same as the fraction of the area being exploited.

This provides the basis for estimating fishing mortality from F = a'/A where a' is the exploitation area associated with the fishing effort and A is the area occupied by the stock.

The exploitation area in this relationship is the product of the area of influence of the gear (a) and the proportion of fish from within the area of influence that are caught (p). The equation is a' = a.p

When considering a single unit of effort, that is when X = 1 and hence F = q, the associated fraction of the area being exploited is the same as the catchability coefficient. The relationship in this event is q = a'/A.

Choice of unit for fishing effort

The relationship between fishing effort and fishing mortality may not always be constant. It will tend towards constancy the more closely the chosen unit of effort is to the catching of the fish. For example, a boat year, a fishing day, and an hour with the net at the bottom, are progressively better choices for an effort unit.

Even better would be an effort unit that encompasses the concept of exploitation area. The horizontal width of the trawl net, and each of trawl duration (i.e. time) and speed, may be known from logbook data. The product of these is the area of influence of the gear.

The concept could be taken even further if an average proportion of fish caught per unit of effort were determined (as from research) or assumed. As indicated earlier the product of this and the area of influence of the gear is the exploitation area.

In practice the unit of effort used in a stock assessment will be dependent on what data are available. Often the only data are fishing days, or fishing hours. These may include not only the component of effort that directly causes fishing mortality, but also other components. Searching or travelling hours are an example of the latter.

Sometimes it is possible to make some refinement. The abalone diving fishery of Victoria (Australia) provides an example. Here the readily available effort is in units of diver hours. This includes a searching component, as well as the time involved in the actual detachment of abalone from the rocks.

In this case it is the searching component of effort that is the more useful, with CPUE as catch per searching hour being the indicator of stock abundance.

Independent research established that on average the time per detachment was 5.1 seconds. Accordingly, a CPUE of 10 abalone per diver hour is equivalent to 10. 14 abalone per searching hour, and 100 abalone per diver hour is equivalent to 116. 5 abalone per searching hour.

Spatial and time aspects of fishing effort

In the context of the fish stock, a unit of effort applied where the stock is dense will cause a higher mortality than if applied where the stock is sparse. In these two circumstances the proportional relationship between mortality and effort will be different. The associated catchability coefficients will be different.

In reflection of the same concept, the consecutive application of a unit of effort on the same fishing location is likely to be associated with declining mortalities per unit effort. Exception would require a rapid redistribution of the fish. Again each unit of effort will be associated with a different catchability coefficient.

These effects are minimised by the statistical aggregation of efforts over small areas (statistical blocks) and small units of time (weeks, months). The effect is also lessened by data aggregation (and averaging), when it can be assumed that the interaction between the fish and fishermen is reasonably random.

Standardisation of fishing effort

As indicated, a unit of effort applied now may cause a different fishing mortality than when applied in the past. This would probably be the case, for example, in the event that effort is measured as fishing days and the average size of boats in the fleet has substantially increased.

A lobster pot boat of 15 m can be expected to exert much less fishing power than one of 30 m. The larger boat would presumably carry more pots. Hence if the historical trend was towards larger boats, CPUEs in units of catch per fishing day will become a progressively biased measure of stock abundance.

An approach to standardisation of efforts is to undertake a comparison of CPUEs between boats (or gears) of different characteristics operating together on the same fishing grounds. The proportional difference in CPUEs can then be incorporated into the unit of effort.

This embodies the concept of relative fishing power (RFP). When comparing a boat to a standard boat the operative equation is RFP_w = CPUE_w/CPUE_s where w and s refer to the boats respectively. In respect to each boat, the new unit of effort will be the product of the old unit and the boat's RFP.

For example, where the monthly effort for a boat is 124 'nominal' fishing hours, and the RFP for the boat is 1.5, then the 'standard' effort will be 186 (= 124 × 1.5) 'standard' fishing hours. The new effort for the fleet will be the sum of the 'standard' efforts for all boats.

Where there is a relationship between RFP and some boat characteristic, it may be more beneficial to estimate 'standard' effort as the product of the 'nominal' effort and the gear characteristic. There would need to be some prior establishment of the relationship.

In the event of establishing a proportional relationship between RFP and dredge width for scallop boats, for example, an appropriate 'standard' effort might be the product of fishing hours and dredge width (or relative dredge width).

In respect to the above, one might arrive at the same choice from a consideration of logic. This could be introduce error as it would require a presumption that the relationship was proportional. It might be linear but not proportional. The safer procedure is to apply the RFP (or other) methodology to actually establish the relationship.

Fish size and fishing effort

A unit of effort applied to small fish will often be associated with less mortality (relative to the stock) than if applied to larger fish. This would occur if the characteristics of the fishing gear or method were such as to be selective for catching large fish. Most fishing is in fact selective for size.

Expanding the relationship between fishing mortality and fishing effort can accommodate this. The modified form is F = q'.q".X where q' and q" are components of the catchability coefficient, one independent and the other dependent on fish size.

In practice the dependent component will be assigned values ranging from zero to unity. The values will be zero for those sizes for which there is no capture. At the other extreme values will be unity for sizes for which the maximum proportion of fish encountering the gear are caught.

There are two broad categories of selectivity effect according to size. Gill net selection is reflected by values of unity in the mid-size ranges that trend to zero for the small and large sizes. Trawl net selection is reflected by values of unity for the larger sizes trending to zero for the smaller sizes.

In respect to each of these categories, relationships can be formulated enabling estimation of the selectivity value for each fish size. Length is usually the preferred size characteristics in such exercises.

The useful relationship in respect to gill net selection is q" = exp(-((((L1+L2)/2)-Ls)^2)/(2.s^2)) where Ls is the optimum selection length and s is the standard deviation of the selection length.

The useful relationship in respect to trawl net selection is q" = 1/(1+exp(S1-S2.(L1+L2)/2)) where S1 and S2 are selection constants. In both equations L1 and L2 are the fish lengths at the start and end of the length interval.

The constants in these relationships can be determined directly from field studies (e.g. mesh selection trials). Alternatively they can be determined in a mathematical comparison of observed and estimated length frequency distributions: the 'best choice' constants being those producing closest agreement.

Recruitment and fishing effort

There can be other factors contributing to a size dependent component of the catchability coefficient. Recruitment, in the sense of presence on the fishing grounds, is one of these. Again this can be accommodated by an expansion of the relationship between fishing mortality and effort.

The modified form is F = q'.q".q"'.X where q', q", and q"' are components of the catchability coefficient, one independent and the other two dependent on fish size. One of the latter reflecting the selection effect and the other the recruitment effect.

The second dependent component will have values ranging from zero to unity. The values will be zero for those sizes not present on the grounds (and hence not caught). At the other extreme values will be unity for sizes that are fully present, reflected as the maximum proportion of fish that are caught.

In practice, there are few situations in which the available data allow a separation of these two size dependent components of the catchability coefficient. Length frequency data from commercial fishing will be a reflection of both effects combined.

Length frequencies from research fishing where non-selective gears are used can be useful. In respect to a diving fishery, for example, commercial operators would be selective by size, while research divers can choose to collect all available sizes. Placing a 'cover' over a trawl net could achieve the same effect.

Natural mortality and fishing effort

Natural mortality is the mortality independent of fishing effort. It is the fraction of the fish dying naturally in the time (and space) interval under consideration. The associated equation is M = Dn/N' where Dn is the natural death number and N' is the mean stock number.

The sum of the two sources of mortality together, total mortality, is the fraction of the fish dying from all causes in the time (and space) interval under consideration. The associated relationships are Z = (C_n + D_n)/N' = M + F = M + q.X.

Prior estimation of Z has relevance to the estimation of the mean population number, from the numbers at the start and end of the interval. The operative equation is N' = (N1 - N2)/Z, where N1 and N2 are the start and end numbers.

Short lived and juvenile fish have high values for M, compared with long-lived and mature-aged fish. Furthermore, F and M are competitive for the same fish. A fish dying from natural causes is not available to be caught, and vice versa.

The capture of a given number of fish from a stock with a high M, adds less to the total mortality, than for a stock with a low M. In the former a greater proportion of the catch is from fish that would otherwise have died naturally during the given time (and space) interval.

As such, it will be important when undertaking stock assessment, not to assume that M is constant over all sizes (and ages), particularly where fishing is occurring over a wide range of fish sizes. Doing so would likely lead to misleading conclusions.

Thompson and Bell's yield estimation

The example spreadsheet (Tables 1 and 2, from Sanders and Dayaratne, 1998) depicts a length-based Thompson and Bell's yield model. It relates to a stock exploited by three gear types (beach seine, gill net, and purse seine). In respect to the gill net component, many mesh sizes are in use. These are not reflected separately in the model. Rather the collective effect of the gill nets is assumed to reflect trawl net selection.

The spreadsheet enables investigation of the likely consequences from applying trial values for the fishing efforts. This can be done for each gear type separately (Table 3) or in combination. If the trial fishing efforts were to range between zero and twice the contemporary values, for example, the relevant fishing effort multiplier would be given values from 0 to 2.

The spreadsheet also allows some possibility to investigate the likely consequences of altering the size composition of the catches, as might be possible in practice from changing fishing gear characteristics or methods, or from changes to management. Inputting alternative trial values for the probability of capture ogives can do this.

The utility of this application is limited within several contexts. The extent to which the spreadsheet is a valid representation of the fishery is constrained by the type of input data available. The use of gill nets of different mesh sizes could be better reflected, for example, if a selection ogive or length frequency data were available for each mesh size.

Its utility is also constrained as the consequence of its reflecting a fishery at equilibrium. As formulated, there is an assumption that the yield from a single cohort during its lifetime is the same as the annual yield from consecutive cohorts. This requires that recruitment and the mortalities remain constant.

If non-equilibrium conditions need to be investigated, this can be achieved using an age-based Thompson and Bell's model associated with a macro (Sanders and Beinssen, 1998). In this the simulation of variable recruitment is achieved using a random number generator in association with a stock/recruitment relationship.

Linking two identical spreadsheets, and copying back and forth between them using the macro, enables depiction of the consecutive years. The population numbers at the start of the year (N1), for all but the recruit cohort, are copies of the population numbers at the end of the year (N2) for the same cohort, from the previous spreadsheet.

Relevant features of Excel

Solver

This feature of Excel allows problem solving by iteration (i.e. trial and error). It can determine the maximum or minimum or chosen values of one cell by changing other cells. This is provided the selected cells are related through formulas in the worksheet.

It is achieved through the following steps:

• On the Tools menu, click Solver.

• In the Set Target Cell box, enter a cell reference for the target cell. The target cell must contain a formula.

• To have the target cell be as large as possible, click Max; as small as possible, click Min; or to be a certain value, click Value of, then type the value into the box.

• In the By Changing Cells box, enter a reference for each adjustable cell, separating each by commas. Up to 200 adjustable cells can be specified.

• In the Subject to the Constraints box, enter any constraints you want to apply.

• Click Solve.

• To keep the solution values in the worksheet, click Keep Solver Solutions in the Solver Results Dialogue box.

• Alternatively, to restore the original data, click Restore Original Values.

It will be important to appreciate that alternative (including erroneous) solutions may be identified. This possibility increases with increase in the number of changing cells. Adding constraints to the inputs can assist in reducing this problem.

This is achieved through the following steps:

• In the Subject to the Constraints box, enter into the Cell Reference box the reference whose value you want to constrain.

• Click the relationship (<=, =, >=, Int, or Bin) that you want between the referenced cell and the constraint.

• In the Constraint box, type a number, cell reference, or name, or formula as required.

• To accept the constraint and add another, click Add.

• Alternatively, to accept the constraint and return to the Solver Parameters dialogue box, click OK.

Data table

This feature provides a convenient way to automatically create tables of results. Either one-variable or two-variable tables can be produced. The former is most appropriate where the results from more than one cell are to be displayed.

The one-variable data table can be achieved through the following steps:

• Decide whether the input values are to be listed down a column (column oriented) or across a row (row oriented).

• Type the list of values you want to substitute in the input cell either down one column or across one row.

• If listed down a column, type the input cell formula in the row above the first value and one cell to the right of the column of values. Type any additional formulas to the right of the first formula.

• Alternatively, if listed across a row, type the formula in the column to the left of the first value and one cell below the row of values. Type any additional formulas below the first formula.

• Select the range of cells that contain the formulas and values you want to substitute.

• On the Data menu, click Table.

• If the data table is column-oriented, type the cell reference for the input cell in the Column input cell box.

• Alternatively, if the data table is row-oriented, type the cell reference for the input cell in the Row input cell box.

The results content of the data table can be converted to fixed values as follows:

• Select all the results values in the data table.
  
• On the Edit menu, click Copy.


• On the Edit Menu, click Paste Special.


• Under Paste, click Values.

Macros

A macro in association with a worksheet allows often repeated tasks to be performed automatically. It is a series of commands and instructions that are stored in a Visual Basic module and can be run whenever you need to run the task.

Creating a macro can be achieved through the following steps:

• On the Tools menu, point to Macro, and then click Record New Macro.

• Enter a letter in the Shortcut Key box if you want to run the macro by pressing a keyboard shortcut key.

• In the Store macro in box, click the location where you want to store the macro.

• To include a description of the macro, type the description in the Description box.

• Click OK.

• Then proceed manually doing actions that you will subsequently want done by the macro.

• After creating a macro it can be run by clicking on the Shortcut Key.

After you record a macro, you can view the macro code with the Visual Basic Editor to correct errors or change what the macro does. To access Visual Basic Editor do the following:

• On the Tools menu, point to Macro, and then click Macros.


• In the Macro name box, enter the name of the macro.


• Click Edit.

Most users will require frequent assistance from Visual Basic Help. The steps required to get this help are as follows:

• On the Tools menu, point to Macro, and then click Visual Basic Editor.

• Click Office Assistant

• In the Assistant, type the method, property, function, statement, or object you want help on, or type a query.

• Click Search, and then click the topic you want.

Concluding comment

Thompson and Bell yield assessments using spreadsheets are a useful approach, particularly for those with modest mathematical and programming skills. They can be applied to multi-gear and multi-species fishery situations. Where there is migration of stock between fishing grounds, this spatial separation can also be accommodated.

One can choose between length-based, age-based, or time-based applications, depending on the available data and the management options to be investigated (Sanders, 1995). While often the outputs will be in reflection of the fishery at equilibrium, spreadsheets can be made dynamic when associated with a macro.

An additional useful feature is the possibility to internally estimate values for some of the input parameters not otherwise available. The obvious example of such a parameter is the number of recruits. Others possibilities include the catchability coefficients and selection/recruitment ogives.

References

Sanders, M. J. 1995. Introduction to Thompson and Bell yield analysis using Excel spreadsheets. FAO Fisheries Circular No. 895: 22 pp.

Sanders, M. J. & P. Dayaratne. 1998. Yield Assessment for the Small Pelagics Fishery occurring along the Northwest, West and South Coasts of Sri Lanka. Asian Fisheries Science 12: 25-40.

Sanders, M. J. & K. H. H. Beinssen. 1998. A comparison of management strategies for the rehabilitation of a fishery: Applied to the fishery for blacklip abalone Haliotis rubra in the Western Zone of Victoria, Australia. Fisheries Research 38:283-301

Table 1: Spreadsheet depiction of the Thompson and Bell's model

Table 2: Spreadsheet inputs, outputs and equations

Table 3: Outputs from the Thompson and Bell's model

Note: Efforts for beach seine and purse seine are kept constant.

Multispecies assessment of the demersal fish stocks along the southeast coast of India

Vivekanandan
Madras Research Centre
Central Marine Fisheries Research Institute, India

Introduction

The analytical stock assessment models such as the Virtual Population Analysis (VPA, or the Cohort Analysis) and the prediction models such as the Thompson and Bell's model and yield/recruit model estimate the stocks of a single species exploited by one fleet. However, the situation in the tropical fisheries, where a fleet exploits several stocks and several fleets compete for exploiting the stocks, calls for multispecies, multifleet stock assessment.

Several approaches for assessing this situation have been suggested during the last 25 years (e.g. FAO, 1978; Pope, 1979, 1980; Pauly and Murphy, 1982; Sparre and Venema, 1992). Most of these models are extensions of the single species/single fleet models. Hence, the theory of single species stock assessment is the background for the multispecies/multifleet theory.

However, many aspects of extending the single species models to multispecies/multifleet theory have to be done with caution by taking into account the nature of the fishery under consideration. This presentation concentrates on the application of multispecies stock assessment models on the demersal finfish stocks along the southeast coast of India.

Situation of the trawl fishery along the southeast coast of India

Along the southeast coast of India, a non-selective gear like the bottom trawl catches, on an average about 50 different species in a single haul. The catches are landed in several landing centers, of which, Chennai Fisheries Harbour is the largest.

The goatfishes Upeneus sulphureus and U. taeniopterus; the threadfin breams Nemipterus japonicus and N. mesoprion; the silverbellies Leiognathus bindus and Secutor insidiator; and the lizardfish Saurida undosquamis contribute about 17 percent to the total trawl landings in the Chennai Fisheries Harbour.

None of these seven species can be considered as the target species. Thus, the catch consisting of a mixture of these species is not determined by the fishing operation but by the availability of fish in the fishing grounds. These species inhabit the same fishing grounds and are caught together.

There are 680 trawlers (overall length: 10 to 14 m; engine hp: 80 to 150) operating from the Chennai Fisheries Harbour. The trawlers operate in grounds, which are up to about 450 km along the shore from the base but land their catches at Chennai. Each voyage lasts for 5 to 7 days. Trawling is conducted 2 to 15 km from the shore at depth ranging from 15 to 70 m. The codend mesh size of the trawlnet is only 10 to 15 mm (stretched measurement).

Trawling is intense along the 450 km length of the coast. The catch and catch rate of the trawlers have substantially decreased during the last one-decade from 31,960 t in 1991 (catch rate: 48.8 kg/h) to 18,772 t in 2000 (catch rate: 18.6 kg/h), causing concern. The government imposed a 45-day ban on the trawlers during April-May from the year 2000.

Procedure followed for multispecies demersal fish stock assessment

The length-frequency data and the length category values of the catch collected during the year 2000 are used here to assess the stocks of the 7 species mentioned above. In a multispecies situation, one cannot estimate the stock and value of each species separately and sum the results of single species assessments such as the Thompson and Bell analysis.

This is because the fishing effort, which gives the MSY or MEY for Upeneus sulphureus will not be the same for the other species. Sparre and Venema (1992) suggested estimation of MEY, rather than MSY for multispecies assessment, by converting yield into units of value for each species. The assessment of the multispecies fishery presented here is based principally on the method suggested by them.

The method works in the following 5 steps:

(i) Estimation of von Bertalanffy growth parameters for each species separately;

(ii) Estimation of total, fishing and natural mortality rates for each species by following traditional methods;

(iii) Length-based cohort analysis for each species separately, which estimates the fishing pattern for each species;

(iv) Length-based yield analysis of the Thompson and Bell's prediction model separately for each species; use of the same F-factor for each prediction of the fishing pattern of the 7 species; application of the value to each length category, and summing up the values of all the 7 species;

(v) From the summed-up values, determination of the F level for MEY by analysing a suitable range of F-factor values.

The assumption behind this method is that when the fishing mortality on the goatfish U. sulphureus is increased by 20 percent, the fishing mortality on the other six species will also be automatically be increased by 20 percent.

Estimation of growth parameters and mortality rates

During the year 2000, samples of 7 demersal finfish species (as mentioned above) were collected every week from the landings of the commercial trawlers at Chennai Fisheries Harbour. Care was taken to collect unbiased samples. Data on the trawl effort, catch and price of length categories of the seven species were collected for 18 days in a month and the length frequency distribution in the sample was weighted for the monthly estimated values.

The von Bertalanffy growth parameters viz. K, L_¥ and t₀ were calculated for each species by tracing the modal progression of length frequencies. The growth parameters thus estimated for the seven species are presented in Table 1.

The total mortality (Z) was calculated by following the length-converted catch curve method by taking length composition data as input (Pauly, 1983). The natural mortality (M) was calculated independently by using the empirical equation suggested by Pauly (1980). The fishing mortality (F) was calculated by subtracting the M from the Z. The exploitation rate (E) was calculated as F/Z. The resulting mortality and exploitation rates calculated for each species are given in Table 1.

Table 1. Growth parameters and mortality rates of seven demersal finfish species off Chennai (southeast coast of India) during the year 2000

Length-based cohort analysis (or Virtual Population Analysis) for U. sulphureus

A virtual population denotes the exploited population, and the analysis estimates the population that must have been present to produce the catch. From observations on the numbers caught in each age/length group and from independent estimates of the natural mortality, the VPA estimates how many fish there must have been in the sea to account for that catch.

The method originated when Derzhavin (1922) combined age data with catch statistics, which was later efficiently used by Fry (1949), and subsequently modified by several others including Gulland (1965) and Pope (1972). Reviews of the methods have been given by Jones (1984) and Pauly (1984) and in the working manual by Sparre and Venema (1992).

The VPA and cohort analysis were first developed as age-based methods. In recent years, length-based methods have been developed, and one such method, the length-based cohort analysis by Jones (1984) is applied here.

The approach for the length-based cohort analysis is basically the same as for the length-converted catch curve. It is assumed that the number of fish in all length classes caught in one year reflects that of a single cohort during its entire life span. This approach can be applied very widely in many commercial fisheries. It is valuable due to the existence of (i) large number of length groups in the fishery; (ii) long series of length composition data; and (iii) a complex and variable fishery in which the F is likely to vary with age (length) and year.

The arithmetic involved is the back calculation from an assumed value of F for the largest length group, because the F value for young fish takes a non-linear form in catches, population numbers, etc. Table 2 shows, as an example, the data set for the fishery of the goatfish Upeneus sulphureus for the year 2000 alone.

In this method, growth is assumed to conform to the von Bertalanffy equation. Length groups are converted into age intervals. The operative equations are:

where L₁ is the midlength of the first length group, and L₂ is the midlength of the succeeding length group.

Table 2. Length groups of Upeneus sulphureus off Chennai during 2000

(K = 0.715/year; =189 mm; t₀ -0.2 year; M = 0.9 year)

The step-by-step calculation procedure for each column in Table 2 is given as follows:

Column A: Grouping of length from minimum to maximum length in the fishery

Column B: Estimation of relative age at midlength of each length group by applying Equation 1

= -0.2-(1/0.715)*ln (1- (54.5/189))= 0.2758

Column C: Estimation of the time taken (t) between the length intervals by applying Eq. 2

= (1/0.715) * ln ((189-54.5)/(189-64.5)) = 0.1081; or

difference in the age between two successive midlengths

= 0.3838 - 0.2758 = 0.108

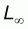Column D: (Natural mortality factor) = ((-L1)/(-L2)) ^M/2K

= ((189-54.5)/(189-64.5)) ^{(0.9/2 * 0.715)}

=1. 0498

Column E: (Number caught) = Estimates of total numbers caught by commercial fishing;

Column F: (Number of survivors) = number of fish that attain the midlength of each length group; or the stock numbers; estimates in this column should start from the last row.

Step 1 = Number caught in the last length group/terminal exploitation rate (F/Z) is assumed as 0.5.

= 41/0.5 = 82

Step 2 = (82 * 2.0884 + 83) * 2.0884 = 531

Step 3 = (531 * 1.3911 + 136) * 1.3911 = 1217; and so on.

Column G: (Exploitation rate) = 4972/(79073 - 67009) = 0.4121;

= 8218/(67009-52510) = 0. 5668; and so on.

Column H: (Fishing mortality) = M*(F/Z)/(1-F/Z)

= 0. 9 * 0.4121/(1-0.4121) = 0.631;

= 0. 9 * 0.5668/(1-0.5668) = 1.1775; and so on

Column I: (Total mortality) = F + M

= 0.631 + 0. 9 = 1.531;

= 1.1775 + 0.9 = 2.0775; and so on.

The basic procedure is simple, but laborious if repeated for several cohorts and also, for several assumptions about the value of F for the largest length group and about M. It is well suited to computer handling.

Though this procedure allows estimates of F for each length group separately, the accuracy of the final estimates for a fishery can be increased by considering that different cohorts are likely to experience similar changes in F from year to year (due to changes in the number of vessels), and for different length groups (due to selectivity of the gears) (Gulland, 1983).

If there are changes only in the number of vessels, the selectivity may not change. If there are changes in the type of gear used, or in fishing grounds, resulting in differences in the sizes of fish caught between the types of gear or fishing grounds, then the selectivity may not be constant from year to year.

The length based cohort analysis can proceed further to calculate the mean number of fish in the sea and their biomass. It may appear that summing the number of survivors (column F) would give the number of fish in the sea. This is not true. The values in column F are simply the number alive at the midlength of each length interval.

To find the mean number of fish in the sea, the mean number between the midlength of one length group to that of the next length group should be weighted by the time (?t) spent between the two mid-lengths, as shown in Table 3.

Table 3. Calculation of yield and biomass using length converted cohort analysis for U. sulphureus of Chennai (K = 0.715/year;M = 0.9/year; = 189 mm; q = 0.000016; b = 2.966)

The mean biomass (column L) during the life span of a cohort (or of all cohorts in a year) can be calculated as follows:

The body weight may also be used to estimate the yield (catch).

The VPA or cohort analysis is used to determine (i) the number of fish that must have been present in the sea based on the numbers in the catch; and (ii) the fishing effort that must have been spent on each length group to catch the numbers. The results obtained in the example shown in Tables 2 and 3 can be interpreted as follows:

(i) There were 7.88 million (column J) individuals in 50-59 mm length group in one cohort of U. sulphureus off Chennai from which 4.972 million (column E) were caught; and the number decreased to 0.046 million and 0.041 million, respectively, in the largest length group.

(ii) Alternatively it also may be considered that (since the catch and sampling is spread over the monthly time scale, and the exploitation is on a mix of cohorts), the estimates are a mix of several cohorts in the year 2000.

(iii) The fishing mortality (column H) was low in the smallest length group (since the recruitment was not full) but was very high in the intermediary length groups.

(iv) The natural mortality (M), which was estimated by other methods, was assumed to be constant at 0.9/year and it was higher than F in the smaller length groups.

(v) The exploitation rate (column G) was generally high (> 0. 5) for many length groups.

(vi) Consequently, the mean biomass (496.1 t; column L) was only marginally higher than the yield (436.7 t; column M).

VPA works well if the catch constitutes a large fraction of the stock (i.e. for a well developed fishery where the F is large). If the proportion of the F is small, its stock estimates becomes uncertain.

Length-based yield analysis for U. sulphureus

The equations used for VPA and cohort analysis can be transformed to predict future yields and biomass at different levels of fishing efforts; i.e. the knowledge of the past fishery can be used to predict the future yields. The prediction models can be applied to forecast the effects of management measures such as closed seasons; changes in minimum mesh sizes and regulation of number of fishing vessels on the catches.

These models provide a direct link between fish stock assessment and fishery resource management. Two prediction models that are widely applied are Thompson and Bell (1934) model and the Yield per recruit model developed by Beverton and Holt (1957). The Thompson and Bell model is used for the present application.

The Thompson and Bell's model is almost an extension of the length-based catch curve method (for the estimation of mortality coefficients) and the cohort analysis (or the VPA). An important aspect of this model is that it allows bioeconomic analysis, if value of the catch and fishing costs are provided as inputs. The four main input parameters required for this model are as follows:

(i) The main input is the range of F values for each length group. The range of F values should be related to the real situation in the fishery, which may be obtained from the VPA analysis or from any other method such as the length-based catch curve method.

(ii) Another important input parameter is the number of recruits, which also may be obtained from the VPA (or cohort analysis).

(iii) The model also requires weight of individual fish in each length group.

(iv) For economic analysis the model requires the price per kg of each length group and fishing costs.

The output parameters are the predictions of catch in numbers, total deaths in numbers, the mean biomass and yield for a combination of different F and M values. The effects of changes in F on the yield, average biomass and value of the catch can be calculated. Since a large number of calculations are involved in this model, it is suggested to use computers.

The calculation procedure for the parameters in Table 4 is given below:

Fishing mortality and M factors are the same as in Table 2. Total mortality = fishing mortality + natural mortality of 0. 9. The mean body weight is calculated from the values q = 0.000016; b=2.966 as in Table 3. The number of survivors (in thousands) in the first length group (50-59mm) is 79073 (refer Table 2).

For the second length group (60-69mm), the number of survivors (in thousands)

= 79073 * [(1/1.0498-(0.631/1.531))/(1.0498-(0.631/1.531))]

= 67009; and so on.

The number caught (in thousands)

= (79073-67009) * (0. 631/1.531) = 4972;

Yield = 4972 * 2.3 = 11436 kg or 11.4 tonnes

Mean biomass = ((79073 - 67009)/1.531)*2. 3 = 18124 kg or 18.1 t

Value of yield (in thousand rupees) = 11.4 * 5 = 57. 0

The calculations are continued for all the length groups. The estimated of number of survivors, number caught, yield and mean biomass are exactly the same as those obtained in the length-based cohort or VPA analysis in Tables 2 and 3.

The calculation in Table 4 have been carried out for the fishing mortality at the current level by considering the current fishing mortality as F-factor = 1. The calculations can be repeated for different F-factors.

In Table 5, the stock parameters have been calculated by considering the F-factor as 0. 5, i.e. what would have been the yield, biomass and value had the fishing mortality been only half of the current level. For this, the fishing mortality for each length group in Table 4 has been divided by two.

In Table 6, the stock parameters have been calculated by considering the F-factor as 1.5. The calculation procedure for each row in Tables 5 and 6 is the same as that in Table 4.

In Table 7, the estimates on the yield, biomass and value for F-factor ranging from 0.25 to 2.00 are given. It could be observed that the yield increases from 245. 2 t at F-factor of 0.25 to 436.7 t at F = 1.00-1.25 but decreases to 399.2 t at F = 2.00 (Fig. 1). The Maximum Sustainable Yield, the MSY (436.7 t) is obtained at the current fishing mortality level (F factor = 1.0).

The mean biomass drastically decreases from 1395.5 t at F-factor 0.25 to 496.1 t at F-factor 1. 00 and further to a mere 186.3 t at F-factor 2.00 (Fig 2). The Maximum Sustainable Economic Yield, MEY is obtained at the F-factor 0.75 (0.1 million US$) (Fig. 3).

Table 4. Analysis of main biomass and yield by using Thompson and Bell's model for the goatfish, U. sulphureus (refer Table 2 and 3); the F factor (x) is considered as 1.0

Table 5. Analysis of mean biomass and yield by using Thompson and Bell's model for the goatfish U. sulphureus (refer Table 4); the F factor (x) is considered as 0.5

The interpretation of the results is that the present fishing level provides the MSY and increase in fishing effort will decrease the yield and drastically reduce the biomass. However, since the MEY is obtained at 75 percent of the present fishing effort, it is advisable to reduce the fishing effort to that level to realise better revenue.

The assumption in this method is that the stock remains in a steady state and all parameters, including recruitment remain constant.

Table 6. Analysis of mean biomass and yield by using Thompson and Bell's model for the goatfish U. sulphureus (refer Table 4), the F factor (x) is considered as 1.5

Table 7. Predicted yield, biomass and value for the yield for different fishing mortalities of U. sulphureus of Chennai

Figure 1. Predicted yield of U. sulphureus for different F-factors

Figure 2. Predicted biomass of U. sulphureus for different F-factors

Figure 3. Value of the yield of U. sulphureus for different F-factors

Yield and value analysis for all species

The cohort analysis and Thompson and Bell yield analysis performed for U. sulphureus was carried out for the other six species (Table 8). For performing the Thompson and Bell analysis, the same F-factors (0.25 to 2.00) applied for U. sulphureus was used for each prediction of the fishing pattern of the other six species. After estimating the values of length categories of each species for each prediction, the values of the yields of all seven species were added (Table 9). The MEY could be achieved at the F-factor of about 0.7 (Fig. 4).

Assessment of combination of multispecies, multifleet fisheries

The seven species mentioned above are caught almost exclusively from trawlers. However, in most tropical fisheries, several fleets of vessels operating different types of craft and gear compete for several species. Stock assessment of these types of fisheries has to consider the combination of economic interaction and technical interaction. The basic input data required are the numbers caught in each length group of all the species under consideration.

Table 8. Predicted yield (t) for different fishing mortalities of seven demersal finfish species of Chennai (southeast India)

Table 9. Predicted value (converted to 000 US $) for different fishing mortalities of seven demersal finfish species of Chennai (southeast coast of India)

Value of seven demersal species for their predicted yield against different F-factors off chenal

The step-by-step calculation, as suggested by Sparre and Venema (1992), is as follows:

Step: 1. Find the average number of fish caught for each length group by all the gears over a time period of several years for every species.

Step: 2. By using the data as input for individual species in the VPA analysis estimate the average number in the population and the overall fishing mortalities for each species. Each F of a length group is the result of the combined fishing mortality created by all gears.

Step: 3. The total F for each length group estimated in Step 2, can be redistributed to each gear by using the following formula:

Fishing mortality of each length group in each species from each gear = Fishing mortality of each length group in each species * (catch (numbers) of each length group from each species from each gear ÷ catch (number) of each length group in each species).

Step: 4. The data obtained in Step 3 and the estimates of the stock numbers (Step 2) form the input for the length-based multispecies Thompson and Bell catch prediction. In this step, the F-factors should be assumed for each gear separately and the estimated fishing mortalities summed up for each species.

Step: 5. Distribute the catches by length group between gears and convert the catches into values.

Step: 6. Finally, sum up the values of the catches of different species for each fleet and for the total multifleet fishery.

Computer programmes on multispecies, multifleet fisheries

ELEFAN III exclusively deals with the VPA. It requires in addition to length frequency data, the monthly catch data. It is necessary that the entire catch from the whole stock must be used, not the catch of a single gear type. This is because, the catch-at-length data representing only part of the fishery is generally not proportional to the total catch.

A routine is available in ELEFAN III, which allows users to store monthly catches and coefficients of length-weight relationship. The routine is in the form of data entry, data editing and viewing and printing. ELEFAN III incorporates three types of VPA, i.e. VPA I, VPA II and VPA III. VPA I estimates the standing stock (in numbers) and fishing mortalities by time interval (month, year, etc) for any given cohort.

The following input is necessary to run VPA I:

(i) a file identifier independent of the files stored in disk;

(ii) the number of periods for which catches are available;

(iii) M and Ft (terminal fishing mortality) estimates (on an annual basis); and

(iv) catches by ages starting with the youngest fish. After providing the inputs, the results are displayed graphically. The user has the option to repeat the analysis by changing the values of M and/or Ft.

VPA II is used to estimate mean standing stock for a stable age distribution, as can be simulated by combining data for several years. It makes use of either catch-at-length data or length frequency data saved in ELEFAN 0. In either type of data, the programme requires the mean annual catch data (in tonnes) represented by the samples and constants for the length-weight relationship.

For length frequency data, in addition to the input requirements, monthly catch (in tonnes) should also be entered to allow conversion of the data from length frequency to catch-at-length type of data. The growth parameters ( and K), as well as M and Ft should be entered. After the requirements are satisfied, the computer estimates the steady-state biomass for each length class. The results in the biomass and other outputs such as the estimated Fi (fishing mortality in the i^th period), catches and population are displayed graphically on the screen.

VPA III provides estimates of monthly lengthwise standing stock and fishing mortality by segregating cohorts through catch-at-length data by means of a set of growth parameters. This approach assumes that little exchange occurs between the monthly cohort, which is true especially for short-lived groups, such as anchovies and penaeid prawns. VPA III incorporates the features of both VPA I and VPA II. A set of monthly length frequency and catch data, , K, M and Ft is the required input.

Using the parameters given, the programme will initialize the array that stores the results for computed monthly summaries. Once the above routine has been completed, the user will be given the opportunity to re-analyse separate cohorts, one after another. The results generated in each cohort analysis will update the array that stores the monthly summaries. The results are displayed graphically.

The programme LCOHOR in the LFSA package can execute Jones' length based cohort analysis. FiSAT analyses the VPA in three forms, viz. age structured VPA, length-structured VPA and length/age VPA in the routine ASSESS. In addition to the ELEFAN, LFSA and FiSAT packages, a package of microcomputer programmes, ANACO (Analysis of COhorts) performs the VPA calculations. The ANACO also offers a number of additional options such as sensitivity analysis.

The LFSA package has two programmes, the TBYR and MIXFISH. The TBYR uses a special version of the Thompson and Bell yield and stock prediction model for the single stock, single fishery situation. The TBYR takes its starting point in the stock numbers by length group calculated by LCOHOR and converts them into age groups. Since conversion from length group to age group is problematic for short-lived species, this programme should be used only for long-lived species (5 years or more).

The other programme in the LFSA is MIXFISH, which is a length-based Thompson and Bell model with option for analysis of a mixed fishery. It is similar to the TBYR, but without the conversion of the length into age groups. It can be used for long-lived as well as short-lived species. Although designed for analysis of a mixed fishery, the MIXFISH contains the single species case as an option. It contains an option for mesh assessment and produces an output showing the total yield for various combinations of effort and L₅₀ percent.

The FiSAT package contains the Thompson and Bell yield and stock prediction for single/multispecies fisheries.

References

Beverton, R. J. H. & S. J. Holt.. 1957. On the dynamics of exploited fish populations. UK Min. Agri. and Fish., Fish. Invest. 19, 533 pp.

Derzhavin, A. N. 1922. The stellate sturgeon (Acipenser stellatus pallas), a biological sketch. Byulleten Bakenskoi Ikthiologiches koi stantsii. 1, 393 pp (in Russian).

FAO. 1978. Some scientific problems of multispecies fisheries. FAO Fish. Tech. Pap. 181, 42 pp.

Fry, F. E. J. 1949. Statistics of a lake trout fishery. Biometrics 5, 27-67.

Gulland, J. A. 1965. Estimation of mortality rates. Cons. Expl. Mer. C. M. 1965, 9 pp.

Gulland, J. A. 1983. Fish Stock Assessment: A Manual of Basic Methods. FAO/Wiley, New York, 223 pp.

Jones, R. 1984. Assessing the effects of changes in exploitation pattern using length composition data (with notes on VPA and cohort analysis). FAO Fish. Tech. Pap. 256, 118 pp.

Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters and mean environmental temperature in 175 fish stocks. J. Cons. Int. Explor. Mer. 39, 175-192.

Pauly, D. 1983. Some simple methods for the assessment of tropical fish stocks. FAO Fish. Tech. Pap. 234, 52 pp.

Pauly, D. 1984. Reply to comments on prerecruit mortality in Gulf of Thailand shrimp stocks. Trans. Amer. Fish. Soc. 113, 404-406 pp.

Pauly, D. & G. I Murphy. (1982). Theory and management of tropical fisheries. ICLARM Conf. Proc. 9, 360 pp.

Pope, J. G. 1972. An investigation of the accuracy of virtual population analysis using cohort analysis. Res. Bull. ICNAF 9, 65-74 pp.

Pope, J. G. 1979. Stock assessment in multispecies fisheries with special reference to the trawl fisheries in the Gulf of Thailand. South China Sea Development and Coordinating Programme, Manila. SCS/DEV/79/19, 106 pp.

Pope, J. G. 1980. Phalanx analysis: an extension on Jone's length cohort analysis to multispecies cohort analysis. ICES C. M. 1980/G 19, 18p. (mimeo).

Sparre, P. & S. C. Venema. 1992. Introduction to Tropical Fish Stock Assessment. FAO Fish Tech. Pap. 306, 376 pp.

Thompson, W. F. & H. Bell. 1934. Biological statistics of the Pacific halibut fishery. 2. Effect of changes in intensity upon total yield, and yield per unit gear. Rep. Internat. Fish. Comm. 8, 48 pp.

Introduction to Ecopath with Ecosim and its use for assessing fishery performance and management policy

Mala Supongpan
Southeast Asian Fisheries Development Center (SEAFDEC)
Bangkok, Thailand

Introduction

Countries in the temperate areas are using single species models to assess their fish stocks. The outcomes of the assessments are used to manage the fishery sustainability. Both input and output controls are widely applied. Input controls are about limiting fishing efforts while output controls are concerned with controlling catches, as with catch quotas.

In tropical areas, the fisheries are often comprised of several species and various fishing gears and methods. Single species models to assess the tropical fish stocks are simultaneously applied case by case. Selected species to represent several fish groups have been used to accommodate the multi-species aspect.

Nine species and eight fleets as well as economic data were used in the BEAM 5 bio-economic modeling of demersal fisheries in the Gulf of Thailand (FAO, 2000). BEAM 5 should be further developed since there are few models that can be applied and suitable for tropical fish stock assessment.

As an additional approach, the development of ecosystem-based models is advancing. An ecosystem is a geographic area including all living organisms (people, plants, animals, and microorganisms), their physical surroundings (such as soil, water, and air), and the natural cycles that sustain them. All of these elements are interconnected. Managing any one resource will affect the others in that ecosystem.

Ecopath with Ecosim (EwE)

Ecopath with Ecosim (EwE) is a suite of software that is being developed for more than a decade, principally at the University of British Columbia's Fishery Centre. The software has some 2,000 plus registered users from more than 120 countries. Hundreds of ecosystems have been investigated using the software and many reports have been published.

EwE has the following three main components:

Ecopath - a static, mass-balanced snapshot of the system;

Ecosim - a time dynamic simulation module for policy exploration; and

Ecospace - a spatial and temporal dynamic module primarily designed for exploring impact and placement of protected areas.

The software package can be used to address ecological questions; evaluate ecosystem effects of fishing; explore management policy options; evaluate impact and placement of marine protected areas; and evaluate the effects of environmental changes.

The foundation of the EwE suite is an Ecopath model (Christensen and Pauly, 1992; Pauly et al. 2000). It provides a static mass-balanced snapshot of the resources in an ecosystem and their interactions. The system is represented by trophicaly linked biomass 'pools'.

The biomass pools consist of a single species, or species groups representing ecological groups. Pools may be further split into juvenile and adult groups that can be linked together in Ecosim.

The input data requirements are relatively simple and generally already available from stock assessment, ecological studies, or from available literature. The input data are biomass (B), total mortality (Z), consumption (Q), diet compositions, and fishery catches.

The parameterization of the model is based on satisfying two 'master' equations. The first equation describes the composition of the production of each group:

Production = catch + predation + net migration + biomass accumulation + other mortality

It aims to describe all mortality factors. Mortality due to old age and diseases are included in the 'other mortality' category.

The second 'master' equation is based on the principle of consumption within a group:

Consumption = production + respiration + unassimilated food

EwE requires input of three of the following four parameters: biomass (B), production/biomass ratio or total mortality coefficient (P/B or Z), consumption/biomass ratio (Q/B), and ecotrophic efficiency (EE) for each of the functional groups. Here, the ecotrophic efficiency expresses the proportion of the production that is used in the system (i.e. it incorporates all production terms apart from the 'other mortality').

If all four basic parameters are available for a group, the program can instead estimate either biomass accumulation or net migration. Ecopath sets up a series of linear equations to solve for unknown values establishing mass-balance in the same operation. It's approach, methods, capabilities and pitfalls are described in detail by Christensen and Walters (2000).

The process of constructing an Ecopath model provides a valuable end product in itself through requiring an explicit synthesis of the work from many researchers. EwE has been applied to the Prince William Sound (Okey and Pauly, 1999), and the Strait of Georgia (Pauly et al. 1998), the Hecate Strait (Haggan and Beattie, 1999). Several North Atlantic models are being created by the Sea Around Us project at the UBC Fisheries Centre.

The model construction process has brought together scientists, researchers and data from state and federal levels of government, international research organizations, universities, public interest groups and private contractors. Key results include the identification of data gaps as well as common goals between collaborating parties were previously hidden or less obvious.

The process is especially important for enabling the interest groups to take ownership of the model it derives. This is especially required when operating at the ecosystem level, where multi-faceted policy goals have to be discussed widely as part of the management process. This is facilitated by the policy exploration methods included in Ecosim.

Ecosim

Ecosim provides a dynamic simulation capability at the ecosystem level, with key initial parameters inherited from the base Ecopath model. The key computational aspects are summarised below.

Use of mass-balance results (from Ecopath) for parameter estimation; variable speed splitting enables efficient modeling of the dynamics of both 'fast' (phytoplankton) and 'slow' groups (whales); effects of micro-scale behaviors on macro-scale rates: and top-down vs. bottom-up control is incorporated explicitly. Also included are the biomass and size structure dynamics for key ecosystem groups, using a mix of differential and difference equations.

As part of this Ecosim incorporates: juvenile size/age structure by monthly cohorts, density- and risk-dependent growth; adult numbers, biomass, mean size accounting via delay-difference equations; stock-recruitment relationship as an 'emergent' property of the competition/predation interactions of juveniles.

Ecosim uses a system of differential equations that express biomass flux rates among pools as a function of time varying biomass and harvest rates (for equations see Walters et al. 1997; Walter, 2000). Predator - prey interactions are moderated by prey behavior to limit exposure to predation, such that biomass flux patterns can show either bottom-up or top down (trophic cascade) control (Walters, 2000). By doing repeated simulations Ecosim allows for the fitting of predicted biomass to time series data.

Time series fitting in Ecosim can evaluate fisheries and environmental effects. Ecosim can thus incorporate (and indeed benefits from) time series data on relative abundance indices (e.g. survey data, catch per unit effort [CPUE] data), absolute abundance estimates, catches, fleet effort, fishing rates and total mortality rates.

Time series data can be available from single species stock assessments for many groups to be incorporated in the model. EwE thus builds on the more traditional stock assessment approaches, using much of the resulting information available and integrating this to the ecosystem level.

The time series fitting from either fishing effort or fishing mortality data are used as driving factors for the Ecosim model run menu. A statistical measure of goodness of fit to the time series data outlined above is generated each time Ecosim is run.

This goodness of fit is a weighted sum of the squared deviations (SS) of log observed biomass from log predicted biomass, scaled in the case of relative abundance data by the maximum likelihood estimate of the relative abundance scaling factor q in the equation: y = qB (y = relative abundance, B = absolute abundance). Each reference data series can be assigned a relative weight representing a prior assessment of relative data reliability.

In addition to the nonlinear optimization routines described above. The fit to data can also be improved in a feedback-process by examining some of the crucial ecological parameters in the EwE model (notably total mortality rates and the settings for top-down/bottom-up control).

It is important to note here that such fitting does not include any 'fiddling-factors' internal to the model, instead the type of question that is addressed after each run is "which species parameters or ecological settings are not set such that the model captures the observed trends over time adequately?"

The inclusion of time series data in EwE facilitates its use for exploring policy options for ecosystem-based fishery management. The time series fitting has been done for a few ecosystems (French Frigate Shoals, Strait of Georgia, Gulf of Thailand, North Sea). A dozen or so more applications are underway. The results so far have been very encouraging.

An important preliminary conclusion is that the model is capable to produce a reasonable fit (e.g. fits that can be compared to those obtained using single species models). This indicates a capability or at least a potential to replicate the known history of the ecosystems. In turn this lends some confidence to how the model can be used for policy exploration.

Using Ecosim for policy exploration

FAO organized a workshop on the 'Use of Ecosystem Models to Investigate Multi-species Management Strategies for Capture Fisheries' at the University of British Columbia (UBC) in July 2000. Forty scientists from all over the world participated and worked with fifteen to twenty EwE models.

The objectives of using EwE were to investigate the impact of different multi-species harvesting strategies on the community structure and fishery yields with a view to identifying preferred harvesting strategies. This was done with particular reference to regulating fishing mortality rates over time, in the contexts of fishery development or recovery from the past overfished status.

The Ecosim module of EwE was updated for the FAO workshop to provide two ways of exploring the impacts of alternative fishing policies:

1. Fishing rates 'sketched' over time and the results (catches, economic performance indicators, biomass changes) examined for each sketch. This is using Ecosim in a 'gaming' mode, where the aim is to encourage rapid exploration of options.

2. Formal optimization methods used to search for fishing policies that would maximize a particular policy goal or 'objective function' for management.

The first approach has been implemented in Ecosim since its first version, and has been widely applied for exploring ecosystem effects from changes in fishing effort. The second approach favoured at the workshop was a newly developed 'open loop' policy exploration simulation developed explicitly for the workshop and incorporated in the EwE software system.

This approach acknowledges that policy may be defined as an approach towards reaching a broadly defined goal. Arguably, most fisheries research has up to now been on policy implementation only, and the intention with the tool is to enable fishery scientists to advise both on policy formulation and on its implementation.

The goal function for policy optimization is defined by the user in Ecosim, based on an evaluation of four weighted policy objectives: maximize fishery rent; maximize social benefits; maximize mandated rebuilding of species; and maximize ecosystem structure or 'health'.

The first of these, maximizing profits, is based on calculating profits as the value of the catch (catch and price by species) less the cost of fishing (fixed + variable costs). Giving a high weight to this objective often results in phasing out most fleets except the most profitable ones, and wiping out of ecological groups competing with or preying on the more valuable target species.

The second objective, maximizing social benefits, is expressed through the employment supported by each fleet. The benefits are calculated as number of jobs relative to the catch value of a specific fleet. Therefore social benefits are largely proportional to fishing effort. Optimizing efforts often leads to even more extreme (with regards to over fishing) fishing scenarios than optimizing for profit.

The maximization of mandated rebuilding of species (or guilds) is incorporated to capture that external pressure (or legal decisions) to preserve or rebuild the population of a given species in a given area. In Ecosim this corresponds to setting a threshold biomass (relative to the biomass in Ecopath) for the species or group, and optimizing towards the fleet effort structure that will most effectively ensure this objective.

The implications of these are case-specific. The findings are that the optimization routine may rigorously exploit (through increased fishing) competitors and predators of the species in question; or at the other extreme that fisheries may be shut down without social or economic considerations (as is indeed often the case when legal considerations take over).

The last objective, maximizing ecosystem structure (or 'health') is inspired by E. P. Odum's description of ecosystem 'maturity', wherein mature ecosystems are dominated by large, long-lived organisms (Christensen, 1995). The default setting incorporated for ecosystem structure is therefore the group-specific biomass/production ratio (B/P). The ecosystem structure optimization often implies the reduction of fishing effort for all fleets except those targeting species with low weighting factors.

Ecosim internally uses a nonlinear optimization procedure known as the Davidson-Fletcher-Powell (DFP) method to iteratively improve an objective function by changing the relative fishing rates. DFP runs the Ecosim model repeatedly while varying these parameters. The parameter variation scheme used by DFP is known as a 'conjugate-gradient' method.

This involves testing alternative parameter values in order to approximate the objective function as a quadratic function of the parameter values. This approximation is used to make further updates of the parameter values. It is one of the more efficient algorithms for complex and highly nonlinear optimization problems.

The objective function can be thought of as a 'multi-criterion objectives', represented as the weighted sum of the economic, social, legal, and ecological objectives. Assigning alternative weights to these components is a way to see how they conflict or trade-off with one another in terms of policy choices.

Indeed, a very interesting aspect of the FAO workshop referred to above was the many discussions that arose on how to balance the policy objectives in the Ecosim routine. There is nothing new in considering these policy objectives even if in an implicit, qualitative way.

It is better to address the objectives through an explicit approach incorporated in a quantitative model. Incorporating the results into present management would obviously require a thorough prior consideration of the inherent risks and uncertainties. It is now very rewarding to be able to participate in a process where the questions addressed are of this sort.

The fishing policy search routine described above estimates time series of relative fleet sizes that would maximize a multi-criterion objective function. In Ecosim, the relative fleet sizes are used to calculate relative fishing mortality rates by each fleet. This is done by assuming the mix of fishing rates over biomass groups remains constant for each fleet (i.e. reducing a fleet by some percentage results in the same percentage decrease in the fishing rates that it causes on all groups caught).

Density-dependent catchability effects can be entered, and if so reductions in biomass for a group may result in the fishing rate remaining high despite reductions in total effort by any/all fleets that harvest it. Despite this caveat, the basic philosophy in the fishing policy search is that future management will be based on control of relative fishing efforts by fleet, rather than on multi-species quota systems.

It is not yet clear that there is any way to implement multi-species quotas safely. Anyway, without either using some arbitrary conservative rule like closing the fleet when it reaches the quota for the first (weakest) species taken or else allowing wasteful discarding of species once their quotas are reached.

If management is to involve regulation of fishing efforts, then in order to track time-varying fishing mortality rate targets as closely as possible, a key practical issue is how to monitor changes in gear efficiency (catchability coefficients). Furthermore, how to set effort limits in each year to account for such changes in efficiency.

Such monitoring is particularly important for fisheries that can show strong density-dependence in catchability. There are at least two possible ways to monitor changes in catchability (gear efficiency). Both ways are based on monitoring fishing mortality rates (F) over time and using the relationship q = F/f, where qt is fishing rate per unit effort and ft is effort.

The first approach is to do traditional biomass stock assessments in each year, and to estimate F (F = C/B, where C is total catch and B is estimated vulnerable stock biomass).

The second approach is to directly monitor the fishing mortality rate, estimating probabilities of harvest using methods such as annual tagging experiments and within-year estimates of relative decrease in fish abundance during fishing 'seasons'.

A routine in Ecosim developed for the FAO workshop referred to above allows users to do 'closed loop policy simulations' to evaluate these monitoring alternatives in terms of their implications for temporal variation in biomass. The idea in the closed loop simulation is to model not only the ecological dynamics over time, but also the dynamics of the stock assessment and regulatory process.

That is, a closed loop simulation includes 'sub-models' for the dynamics of assessment (data gathering, random and systematic errors in biomass and fishing rate estimates), and for the implementation of assessment results through limitation of annual fishing efforts.

The closed loop simulation module includes options to decide how many closed loop stochastic simulation trials to do; to set the type of annual assessment to be used (F = C/B versus F directly from tags); to set the accuracy of the annual assessment procedures (coefficient of variation of annual biomass or F estimates, by stock); to set value or important weights for the F's caused on various species by each fishing fleet; and do the simulation trials and display results on time series and mean value.

The value weights are used for each fleet/species combination to calculate weighted average catchability (q) for each fleet. Some species will be more important than others, in terms of the effects that they might be allowed to have on effort reduction and q increasing over time.

Closed loop policy simulations could obviously include a wide range of complications related to the details of annual stock assessment procedures, survey designs, and methods for direct F estimation. Using other assessment modeling tools are suggested to examine these details and need only overall performance information consideration (coefficients of variation in estimates).

Application of the Ecopath with Ecosim (EwE) to tropical fisheries management

There have been several trial studies in Thailand using Ecopath and Ecopath with Ecosim during the last decade. The studies were included both freshwater and marine ecosystems.

Chookajorn et al. (1994) studied the evolution of trophic relationships in Ubolratana Reservoir (Thailand) using a multi-species trophic model. Jutagate et al. (2002) also studied the freshwater ecosystems in Sirinthorn (Thailand) and Nam Ngum (Laos) Reservoirs. The output from the Ecopath model indicated similar ecosystems in both reservoirs. Both man made reservoirs were productive, with the zooplankton eating fish being the target species of fishing operations.

Christensen (1998) reported the marine ecosystem analysis of the Gulf of Thailand. Two mass balance trophic models were constructed to describe the Gulf of Thailand ecosystem within the depth range of ten to fifty meters. Ecosim, was used successfully to reproduce the 1980 state of the fishery based on a 1963 model, and also showed the development in catches.

Buchary (1999) evaluated the effect of the 1980 trawl ban in the Java Sea (Indonesia) using an ecosystem-based approach. The results showed that the Java Sea in mid-1970s was a moderately mature and stable ecosystem, thus relatively resilient to perturbations.

Various scenarios that were simulated suggested that the Java Sea was resilient enough to absorb perturbations, mainly by creating alternative stable states. However, these alternative stable states involved the loss of at least some parts of the initial food web structure. In all cases, this involved the increase of economically low value species at the cost of the loss of economically high value species.

EwE has also been used to evaluate the possibility of using marine reserves to control fishing mortality (Guenette, 2000). Results showed that very large marine reserves (80 percent) by themselves could provide a hedge against mismanagement, while a 50 percent reserve would have only showed the decrease of the fish population. The result also suggested that adding season closures could help control fishing mortality, although possible temporal effort displacement was not investigated.

The principal benefits of season closures would be to protect the spawning aggregations rather than controlling fishing mortality. Every management scenario that was efficient at controlling fishing mortality implied decreasing the catch before the stock started rebuilding.

Supongpan et al. (2000) also reported on the use of ecosystem models to investigate multi-species management strategies for capture fisheries in the Gulf of Thailand. EwE was used to simulate both open and closed loop policies to maximize the economic, social sustainability and ecosystem stability.

The results of the open loop simulation showed the optimum fishing efforts over time to get the best economic profit required reducing the efforts of pair trawlers by about 20 percent, beam trawl and push net by 50 percent of the present efforts. The increasing efforts of otter board trawl, purse seine and other gears by about 40 percent 10 percent and 90 percent respectively should be done to achieve balance of the whole fisheries to get the best profit.

Vibunpunt et al. (2000) described a trophic model of the coastal fisheries ecosystem in the Gulf of Thailand.

The Ecopath Working Group at the FAO Workshop (2001) made the most extensive use of the available long time series of data on catch and effort including economic information. EwE simulated prey-predator relationships through a mass balance approach. Changes in relative effort for each of the six fleets considered during the period 1973 to 1993 were then used to drive the model over the time period.

The results indicated a complete ban of push net fishing would have minor effect on biomass, catches and profits. This can be assumed to reflect the overall very low catch level represented by the push net fleet. Avoiding the capture of juveniles by banning all small mesh sizes led to a marked decrease in overall catch level, while the value of the catch only decreased marginally.

The reduced catches of small fish does not lead to any marked improvement in the state of the overall system, indicating that such a measure would be inadequate for changing the gross overfishing in the Gulf of Thailand.

Limitations and constraints

(a) Data requirement

Data for a single year or several years (i.e. time series) can be used with EwE. These will include biological data by species or by group of species relevant to each fleet, diet compositions for estimating for prey-predator relationship, growth and mortality parameters, fishery data (catch and effort, fish price by fleet, production and biomass; P/B can be replaced by Z), social and economic information.

The ecological fish group categorisation by trophic level can be determined using the Fishbase database available from ICLARM, as well as other reports and publications.

The large requirement for data makes it difficult to apply the software to developing country situations. In particular time series statistical data collection are rather difficult and expensive to get.

Another problem is the EE estimation if the P/B and Q/B values are too high or low. In this event the simulation process will not proceed further. If in the first step, data input is good then the Ecopath will allow the program to work accordingly.

(b) Obstruction by the written program

It is known that in tropical countries, the fisheries are much more complex than in the temperate countries. These fisheries are always dealing with several species and various fleets with different levels of fishing operation. Sometimes, the process of running Ecosim will have overflow results caused by too much data input. In this case, the ordinary users can do nothing about the program due to inadequate programming knowledge and lack of experience in Access and Visual Basic in which the program has been basically developed.

(c) Computer constraint

In almost all the developing countries computers and internet access are limited. The capacity and the efficiency of the computer systems are still low. Updating information and downloading of some data (e.g. Fishbase, EwE) are not possible in several cases. If the Window and the Microsoft Office used do not matched the requirements of EwE, the program will not run. This is another problem for the developing countries, especially the countries in Asia.

(d) Need for more training courses

Beginners who want to explore the program will have difficulties when inputting real data. The program will not easily allow the beginners to pass through. Need for training to use the program is considered of priority importance. Basic knowledge of the assumptions of the ecosystem model, food assimilation including energy flow and respiration are also important. Even though the user may read the user's guide (Christensen, Walters and Pauly, 2000), it will nevertheless take a long time to successfully use the software, if there is no guidance or training.

References

Buchary, Eny Anggraini. 1999. Evaluation effect of the 1980 trawl ban in the Java Sea, Indonesia: an ecosystem-based appproach. University of British Columbia, Canada. (MA thesis)

Chookajorn, T.; Y. Leenanond; J. Moreau & B. Srichareondham. 1994. Evolution of trophic relationship in Ubolratana reservoir (Thailand) as described using a multi-species trophic model. Asian Fish. Sci., 7: 201-213.

Christensen, V. 1995. Ecosystem maturity - towards quantification. Ecol. Modelling, 7:3-32.

Christensen, V. 1998. Fishery induced changes in a marine ecosystem: insights from models of the Gulf of Thailand. Journal of Fish Biology 53 (Supplement A), pp. 128-142.

Christensen, V. & C. Walters. 2000. Ecopath with Ecosim: methods, capabilities and limitations. In D. Pauly and T. Pitcher, eds. Methods for assessing the impact of fisheries on marine ecosystems of the north Atlantic. Fisheries Centre Research Reports 8(2).

Christensen, V. & D. Pauly. 1992. A guide to the ECOPATH II program (version 2. 1). ICLARM Software 6, 72 p.

Christensen, V., C. J. Walters & D. Pauly. 2000. Ecopath with Ecosim - A user's guide. Vancouver, Canada, Univ. of British Columbia Fisheries Centre and ICLARM, Penang, Malaysia.

FAO, 2001. Report of a bio-economic modelling workshop and a policy dialogue meeting on the Thai demersal fisheries in the Gulf of Thailand, Hua Hin, Thailand, 31 May - 9 June 2000.

Gunnette, Sylvie. 2000. Marine reserves for the northern cod. University of British Columbia, Canada. (Ph. D. thesis)

Haggan, N. & A. Beattie (Editors). 1999. Back to the future: reconstructing the Hecate Strait ecosystem. Fisheries Centre Research Reports 7(3): 65 p.

Okey, T. A. & D. Pauly. 1999. A mass-balanced model of trophic flows in Prince William Sound: de-compartmentalizing ecosystem knowledge. In: S. Keller, ed. Ecosystem approaches for fisheries management, pp. 621-635. Fairbanks, University of Alaska Sea Grant.

Pauly, D., V. Christensen & C. Walters. 2000. Ecopath, Ecosim, and Ecospace as tools for evaluating ecosystem impact of fisheries. ICES J. Mar. Sci. 57: 697-706.

Pauly, D. D. Preikshot & T. Pitcher (Editors). 1998. Back to the future: reconstructing the Strait of Georgia ecosystem. Fisheries Centre Research Reports, 6(5): 99 p.

Supongpan, M., V. Christensen, C. Walters & T. Pitcher. 2000. The use of ecosystem models to investigate multi-species management strategies for capture fisheries in the Gulf of Thailand. A paper presented for the Workshop on the Use of Ecosystem Models to Investigate Multi-species Management Strategies for Capture Fisheries held by FAO/UBC, Canada, July 2000.

Jutagate, T., N. S. Mattson, J. Moreau, B. Srichareondham & M. Kumsri. 2002. Ecosystem in Sirinthorn and Nam Ngum Reservoirs: a comparison. Kasetsart University Fisheries Research Bulletin, No. 24, 14 p.

Vibunpun, S., N. Khongchai, J. Seng-eid, M. Eiamsa-ard & M. Supongpan. 2000. Trophic model of the coastal fisheries ecosystem in the Gulf of Thailand. A paper submitted to the ICLARM/ADB Project: Sustainable Management of Coastal Fish Stocks in Asia.

Walters, C.J. 2000. Impacts of dispersal, ecological interactions and fishing effort. Bull. Mar. Sci. 66(3).

Walters, C. J., V. Christensen & D. Pauly. 1997. Structuring dynamic models of exploited ecosystems from trophic mass-balance assessments. Rev. Fish Biol. Fish. 7: 139-172.

Application of an ecosystem model on the fish stocks in the southwest coast of India

Vivekanandan
Madras Research Centre
Central Marine Fisheries Research Institute, India

Introduction

The traditional stock assessment models are concerned only with what happens to a single species and with the catch and CPUE relating to that species. In reality, fishing induces much larger changes at the ecological and biological levels on the abundance, species composition, age and size structure, sex ratio, genetic structure, reproduction, and prey-predator interactions among the fish stocks.

In short, fishing alters the structure and function of marine ecosystem (Dayton, 1998). Hence, fish stocks cannot be understood and quantified fully without a thorough knowledge of their environment, their associates and their interactions. The single species stock assessment models are not properly concerned about food, predators, competitors with which the target species interacts, nor about the physical environment to which the species is exposed.

By citing assessments on the tropical marine fish stocks, Vivekanandan (2001) has linked the resilience of tropical fish stocks to the inadequacies of the existing single species stock assessment models, most of which assume steady-state environment. The concept that the fish stocks should be assessed with ecosystem considerations is gaining importance in recent years.

The understanding that the fish and other aquatic living resources are an integral part of their ecosystems is not new. The idea is being put into practice recently (since the 1990s) through the application of effective fisheries ecosystem assessment tools.

The methods now available for the analysis of fisheries ecosystem include mass balance trophic models designed for straightforward construction, parameterization and analysis of fish stocks, their trophic levels and their bio-energetic parameters, associated with the physical environmental parameters.

Under the ADB-RETA 5766 project of ICLARM, the Central Marine Fisheries Research Institute (Cochin, India) applied Ecopath, an ecosystem model for the fisheries along the southwest coast of India (CMFRI, 2002). The method of application of Ecopath and the possible interpretations of the results are presented here.

Principles of Ecopath (the mass-balance model)

Polovina (1984) initially presented the application of Ecopath. It has now been developed as a computer software package by combining with various approaches of theoretical ecology. This software is now used for estimating biomass and food consumption of species or groups of species of aquatic ecosystems.

The software has been further optimized for direct use in fisheries assessment as well as for addressing environmental questions through the inclusion of a temporal dynamic model (Ecosim) and the spatial dynamic model (Ecospace).

Once an Ecopath model is constructed for an ecosystem, it is possible to have an overview of the resources and the feeding interactions in the ecosystem. It is also possible to analyze the ecosystem in detail, and through Ecosim, simulate the effects of changes in fishing pressure, and given time series data, evaluate the relative impact of fisheries and the environment. The analysis provides practical approaches for managing fisheries resources in the ecosystem.

The Ecopath considers that several functional groups constitute each ecosystem. In Figure 1, for instance, the ecosystem A has 16 functional groups. Each group may be a single species (for example, the oil sardine), or related species groups (sardines or the same taxonomic groups, the clupeids) or species sharing common food (plankton feeders) or same size/age groups. There are several other functional groups in the ecosystem A, such as the other species, species groups, carnivores, apex predators, etc.

Fig. 1. Flow of matter within and between ecosystems (a hypothetical example)

Within each functional group, there is interaction through flow of matter and energy; and these interactions add up to a larger flow within the ecosystem. This added-up flow within the ecosystem A will be larger than the interactions of the ecosystem A with its adjacent ecosystem, B.

The ecosystem approach does not assume steady state (as in the case of single species stock assessment models) but considers mass balance in the ecosystem through flow of matter and energy over a time period. The flow of energy within and between the functional groups is best described by two master equations in the Ecopath model. The first equation is the energy balance for each functional group.

Consumption = Production + Respiration + Faeces + Urine (Eq. 1)

Hence, production is linked to consumption.

The second equation splits production as follows:

Production = Catches + Predation mortality + Biomass accumulation + Net migration + Other mortalities (Eq. 2)

Predation mortality is the factor, which links the different functional groups in an ecosystem. Mortality for a prey is consumption of a predator, i.e. the prey in the functional group 1 (in Fig. 1) may be consumed by the functional group 14, thereby providing the linkage.

Thus the network of flows of matter (= biomass) within an ecosystem links the plants with the herbivores, and the latter with the carnivores and predators. These linkages are commonly depicted as a food web and the position of each functional group within the food web is known as trophic level. Figure 2 gives an example of a simplified, hypothetical food web and the trophic level of each functional group in the food web.

Fig. 2. A simplified, hypothetical food web in the marine ecosystem

The phytoplankton and detritus have by definition a trophic level of 1, while herbivores and detritivores have a trophic level of 2. Small carnivores feeding exclusively on herbivores and/or detritivores have a trophic level of 3, and so on. However, the functional groups do not necessarily have trophic levels of exactly 3 or 4 but have intermediate fractional values since they consume several types of prey, which are in different trophic levels.

For instance, the predatory seerfishes, which feed on carnivores like the barracudas (which have a trophic level of 4.0), could not be assigned trophic level of 5.0 since they feed on the sardines (which are low in trophic level, i.e. 2.2) also. Hence, the seerfishes end up with trophic level of 4.4. Due to this reason, the trophic levels of top predators in marine ecosystems do not exceed 5.

Since the food web links the different functional groups in an ecosystem, information on diet composition is important for understanding the dynamics of the ecosystems. Construction of the food web is relevant to fisheries assessment and management since the networks of flows are affected directly by fishing.

For instance, if fishing removes predatory fish above the trophic level 4, there will be proliferation of small and medium carnivores at the next trophic level, i.e. between 3 and 4 (due to reduction or absence of predation upon them). Consequently, there will be competition for prey at trophic levels < 3.

FishBase, developed by Froese and Pauly (2001) at ICLARM, Penang, is an extensive database, which provides key information on all 25,000 finfish species of the world. It is available on CD-ROM and on the internet (www.fishbase.org). Topics covered in the FishBase include taxonomy, population dynamics, reproduction, genetics, trophic ecology and human uses.

The website receives over a million hits/month from a wide variety of users (Froese, 2001). The FishBase provides trophic level values for thousands of species of finfishes by adopting the following approach: A consumer eating 40 percent phytoplankton (with trophic level 1) and 60 percent herbivores (with trophic level 2) will have a trophic level of 1 + (0.4 * 1 + 0.6 * 2) = 2.6 (the first number 1 is the definitional trophic level assigned to phytoplankton).

In its present form, Ecopath parameterizes Equation 2 as follows:

Pi = Yi + Bi * B2i + Ei + Bai + Pi * (1 - EEi) (Eq. 3)

where Pi = total production rate of (i); Yi = total catch rate of (i); Bi = biomass of the group; M2i = total predation rate of (i); Ei = net migration rate (emigration minus immigration), BAi = biomass accumulation rate for (i); Pi * (1 - EEi) = other natural mortality rate for (i); and EEi = ecotrophic efficiency, which is the proportion of the production, which is utilized in the system.

The Equation 3 can be re-written as

where P/Bi = production/biomass ratio; Q/Bj = consumption/biomass ratio; DCji = fraction of prey (i) in the average diet of predator (j). The Pi is calculated as the product of Bi, the biomass of (i) and Pi/Bi, the production/biomass ratio for group (i). The Pi/Bi under most conditions corresponds to the total mortality rate, Z.

The predation mortality, M2, serves to link predators and prey as

where summation is for all (n) predator groups (j) feeding on group (i); Qj = total consumption rate for group (j); DCji = fraction of predator (j)'s diet contributed by prey (i). Qj is calculated as the product of Bj (the biomass of group (j)) and Qj/Bj (the consumption/biomass ratio for group (j)).

An important implication of Equation 5 is that information about predator consumption rates and diets concerning a given prey can be used to estimate the predation mortality for the group. Alternatively, if the predation mortality for a given prey is known, the equation can be used to estimate the consumption rates for one or more predators.

The data requirements for Ecopath are very limited in comparison to those for traditional simulation models. All parameters used to construct an Ecopath model need not be entered. The Ecopath links the production of each group with the consumption of all groups, and uses the linkages to estimate missing parameters based on Equation 2 that production from any of the species groups has to end somewhere in the system.

Catches, biomass, P/B and diets must always be entered, and entry for the other parameters is optional. Consumption is calculated from the Q/B and biomass. The set of linear equations can be solved even if, for any of the groups, one or more of the basic input parameters (B, P/B, Q/B and EE) are not known.

The recent versions of Ecopath are combined with a number of related modules such as Ecosim, Ecospace, and Ecoranger.

Fishery along the southwest coast of India

The southwest coast of India extends from 8^oN to 16^oN comprising of the maritime states of Kerala, Karnataka and Goa. The length of the coastline is 994 km and the continental shelf area is 75,390 km². The coast receives copious rain during the southwest monsoon period from June to September. Due to strong upwelling during the southwest monsoon, the coast is characterized by high levels of nutrients such as phosphate, nitrate and silicate in the surface waters. The coast is rich in phytoplankton and zooplankton biomass compared to the other coastal waters of India.

The fishing grounds along the SW coast are quite extensive and very productive. The annual average fish landing along the SW coast was 620,000 t during 1970-2000, which was 37 percent of the all India landings. The ecosystem is characterized by the abundance of small pelagics such as the oil sardine, other sardines, whitebaits and Indian mackerel.

Most of the area is suitable for trawling and the threadfin breams, lizardfishes, flatfishes and penaeid prawns contribute high percentage to the landings. An array of craft and gear combinations are being employed by the commercial fishing sector. Among the mechanized vessels, the trawlers are the most common. Gillnets, boatseines and ringseines of various dimensions are commonly used by the artisanal sector.

Application of Ecopath for the fisheries along the SW coast

For the application of Ecopath, the Central Marine Fisheries Research Institute, Cochin (India) used the estimated landings from all the gears operated by commercial vessels along the SW coast during 1996. The method of analysis followed by the CMFRI (2001) for the SW coast of India is given below.

Firstly, the ecosystem along the SW coast was categorized into 11 ecogroups based on the feeding habits and ecological niche of the species groups (Table 1). The annual production/biomass ratios (P/B) for the ecogroups were considered equal to the instantaneous rate of total mortality. The Z values estimated by earlier researchers for representative species under each ecogroup occurring along the SW coast were used. Hence, the errors and limitations that affected the estimation of these parameters will be included in the estimates of production.

Table 1. Ecological groupings used for Ecopath analysis for the fisheries resources along the southwest coast of India

The P/B ratio was generally high for all the groups and very high particularly for the demersal feeders (4.3) and the detritivores (12.0). For phytoplankton and zooplankton, the P/B ratios were set at 70 and 40, respectively. The annual consumption/biomass ratio (Q/B) for each ecogroup was estimated following the empirical equation suggested by Pauly et al. (1990).

Q/B = 10 ^6.37 0.0313^Tk W_¥ ^-0.168 1.38 ^Pf 1.87 ^Hd (Eq. 6)

where Tk = 1000 (T^o + 273), T^o = average annual sea surface temperature, W_¥ = asymptotic weight (g) of the species, which contributed maximally to the biomass; Pf = 1 for large predators and zooplankton feeders and 0 for other feeding types; and HD = 0 for carnivores and 1 for herbivores and detritivores.

As data on ecotrophic efficiency (EE) were not available, it was assumed that the EE for the different ecogroups ranged from 0.65 to 0.95 and a conservative value of 0.75 was assumed for phytoplankton following Mendoza (1993). Assimilation in all the groups was considered as 80 percent of consumption, which is the default value in the programme, following Winberg (1956). The basic input parameters for the year 1996 are given in Table 2.

Table 2. Basic input parameters for the southwest coast of India for the 1996 for Ecopath analysis

The detrital biomass was calculated by employing the following empirical relationship suggested by Pauly (1993):

log D = 0.954 log PP + 0.863 log E - 2.41 (Eq. 7)

where D = detrital biomass (g C/m²); PP = primary production (182 g C/m²/year; Pant, 1992); E = euphotic layer depth (40 m). The detrital biomass thus calculated was 426 t/km².

The diet composition has been studied for a number of fishes occurring along the Indian coast by several researchers. However, there is high level of redundancy in the different variables applied for diet composition analysis. Moreover, most of the studies simply give a list of prey items and do not provide the weight of different prey species in the diet. Hence, wherever diet composition was not available as required, information available in FishBase was used.

The diet composition thus constructed for different groups is given in Table 3. The diet composition of the large predators was considered to consist mostly of plankton feeders (0.3) such as the clupeids, which is the abundant group along the SW coast. The other diet components were medium predators (0.2) such as the lizardfish, seabreams and cephalopods; demersal feeders (0.1), etc; and young ones of their own group (0. 01).

Table 3. Diet composition of ecogroups in the southwest coast ecosystem

It was also considered that import (0.09) would have occurred in the form of migration, especially of the tunas such as Thunnus tonggol from other ecosystems and sharks such as Carcharhinus spp from the offshore into the inshore fishing grounds. It is known that the seerfish, Scomberomorus commerson, also undertakes coastal migration.

Phytoplankton primary production was considered as 0.5 g C/m²/day following Pant (1992). A conversion factor of 0.06 g C = 1 g wet weight (Walsh, 1981) was employed for converting carbon values into phytoplankton.

One of the characteristics of mass balance ecosystem models is that all flows and biomasses can be shown in a single flow diagram. The flow diagram for the SW coast, as estimated by the Ecopath, is given in Figure 3. Flows from the detritus were as important as flows from phytoplankton.

For the pelagics, the main flow is determined by the interaction between phytoplankton, zooplankton and plankton feeders. For the demersals, the flow is associated with detritus and detritivores. The plankton feeders and detritivores were low-level consumers (mean trophic level: 2.0 to 2.2). Molluscan feeders and carnivorous mesopelagics were at intermediate levels (trophic level: 3.0 to 3.3), and large predators at the higher trophic level (4.0).

The Ecopath gives the mixed trophic impacts within the ecosystem (Fig. 4). As a prey, a group causes a positive impact on its predators. As a direct predator, it has a negative impact on its prey. The impact can be direct or indirect. Phytoplankton, zooplankton and detritus had positive impacts on most other groups. The impact was greatest on their direct predators; for instance, the impact of phytoplankton was greatest for the zooplankton; and the impact of zooplankton was high for the plankton feeding fishes.

Negative impacts on phytoplankton were due to zooplankton as consumer (of phytoplankton) or as competitor (for phytoplankton feeding fish). Phytoplankton and zooplankton had a strong positive indirect impact on the fishery, as plankton is the main prey of the small pelagic fishes, which in turn is the main fishery along the SW coast. Detritivorous benthos represented a positive impact as prey to carnivorous benthos and benthic feeding fishes. The detritus box impacted the benthic fishes via the detritivores.

The Ecopath provides important information (Table 4) that may allow identification of the status of an ecosystem in terms of maturity and to compare different systems. The total system throughput is equal to the sum of all flows (consumption, exports, respiratory flows and flows into the detritus) within an ecosystem.

Figure 3. Ecopath flow diagram for the southwest coast of India for the year 1996

P = production; B = biomass; Q = consumption; all are t/km

Figure 4. Mixed trophic impacts of groups in the southwest coast ecosystem; positive impacts are shown above each baseline in dark rectangles; negative impacts are shown each baseline in open rectangles

Table 4. Comparison of the biomass flow in the southwest coast of India (CMFRI, 2001) as estimated by Ecopath

The value of 14,083 t/km²/year obtained for the SW coast of India is high compared to several other ecosystems in terms of flow per unit area (for instance, 7,621 t/km²/year for the northeastern Venezuala shelf ecosystem; Mendoza, 1993). An important reason for the high amount of throughput is linked to very high primary production (9,091 t/km²/year) and the high detritus biomass (426 t/km²/year).

The other summary statistics in Table 4 are meant to express the relative degree of maturity of an ecosystem. The relevance of some important parameters are explained below:

(i) Mean trophic level of the catch provides information on the mean trophic level of fishing. Fishing down marine food web occurs when large predators disappear from the ecosystems.

(ii) Gross efficiency of the fishery correlates the primary production and potential fishery yields. The value will be higher if the fishery harvests fish low in the food chain (e.g. an upwelling fishery) than the fishery, which concentrates on apex predators.

(iii) Total primary production/total respiration is considered to be an important ratio for describing the maturity of an ecosystem. In the early developmental stages of a system, production is expected to exceed respiration, leading to a ratio greater than 1. In mature systems, the ratio should approach 1, i.e. the energy that is fixed is approximately balanced by the cost of maintenance.

(iv) Net system production is the difference between total primary production and total respiration. The net system production will be large in immature systems and close to zero in mature ones.

(v) Total primary production/total biomass is also expected to be a function of its maturity. In immature systems, production exceeds respiration, and as a consequence, one can expect biomass to accumulate over time. This in turn will influence the system PP/B ratio, which may decrease.

(vi) Total biomass/total throughput can be expected to increase to a maximum for the most mature stages of a system.

(vii) The Connectance Index (CI) is the ratio of the number of actual links to the number of possible links in a given food web. For instance, if there are three species, X, Y and Z in an ecosystem, the following three links are possible: X with Y, X with Z, and Y with Z (Fig. 5a). However, the actual links may be only between X and Y, and X and Z, thus resulting in CI = (2/3) = 0.66.
For several ecosystems, it has been observed that the actual number of links in a food web is roughly proportional to the number of groups in the system. The food chain structure tends to change from linear to web-like as the system matures. The level of taxonomic details used to represent prey groups largely determines the value of CI.

(viii) System omnivory index is the average omnivory index of all consumers weighted by the logarithm of each consumer's food intake. It is a measure of how the feeding interactions are distributed between trophic levels. Since interactions of nearly all groups are possible during the ontogenetic development in aquatic organisms, the system omnivory index recognizes weblike features. Considering three species (X, Y and Z) and three size categories, large (l), medium (m) and small (s) in each species, there will be several combinations of interactions, some of which are given in Figure 5b. If the three species belong to different trophic levels, the interactions assume weblike features and determine the recruitment of the prey species.

Figure 5a. Links between species in an ecosystem

Figure 5b. Interaction between species in an ecosystem

The Ecopath model can be developed as a powerful tool not only for gaining an insight into the functioning of the ecosystem but also for evolving fisheries management plans. The analysis for the SW coast of India indicated that the harvestable biomass of the plankton feeding pelagics such as the clupeids, Indian mackerel and scads is very high (14.6 t/km²) compared to the annual average catches (6.7 t/km²) along the SW coast (Table 5) and hence, there is scope for increasing the catches of the plankton feeders to the tune of 7.9 t/km² (Fig. 6).

Table 5. Comparison of biomass estimated by Ecopath and catch from commercial vessels along the southwest coast India during 1996

On the other hand, the catches of the several other ecogroups, especially the demersals (major perches, threadfin breams, goatfishes, sciaenids, flatfishes, whitefish etc.) and the detritivores (penaeid shrimps) have exceeded the harvestable biomass by 0.1 to 2.2 t/km².

The analysis provided the following important clues on the imbalance in the commercial operations along the southwest coast:

• Gears employed for the exploitation of the demersal resources, particularly the bottom trawls are excessively used. The trawlable biomass appears to be overexploited and a reduction the trawl effort is necessary.

• Gears employed for the exploitation of pelagic resources are either underutilized or are not utilized. Considering the scope for increasing the catches of the plankton feeders, which are pelagic, it has been suggested that pelagic/mid-water trawl, which is not commercially practiced along the Indian coast, may be attempted.

Figure 6. Status of exploitation of ecogroups along the southwest coast of India as estimated by Ecopath model; the values are t/km²

The idea of presenting the Ecopath analysis for the SW coast of India is to introduce the readers to the principles and working of the mass balance model. It should not be viewed as a complete analysis of the ecosystem. It is important to stress here that the model is incomplete because the apex predators (such as the marine mammals, reptiles and birds) have not been included due to lack of adequate data.

Another shortcoming stems from the fact that bacterial densities have not been considered; and the imports and exports are not known for all the functional groups (except the import, which was set for only large predators at 0.08), assuming that interactions with adjacent ecosystems were negligible.

The interest in ecosystem based assessment and management is steadily growing throughout the world. Ecosystem models call for information from all parts of an ecosystem, especially from the exploited part of the system. Therefore such models rely heavily on information from single species stock assessments.

Ecosystem-based assessment approaches are not going to replace single species stock assessment, but they will supplement and enrich them. If no data are available at the individual or species level, there is no way to embark on modelling at the ecosystem level. Real ecosystems have dynamics far more complex than represented in Ecopath and Ecosim.

The Ecopath models assemble the available information in a framework and enable evaluation of the data and pinpoint critical gaps in the present knowledge. As more and more information are included in the model, the estimates are improved and the uncertainties are reduced.

When fitting Ecopath to the data, the same risks as in single species assessment are encountered, such as incorrect biomass estimation, misinterpretation of trend data, and failure to assess the effects of environmental changes. However, the Ecopath with Ecosim has been found to be very helpful in interpreting effects of large scale and persistent changes in the productivity at the ecosystem level. It is particularly helpful in understanding the relative importance of fishing versus environmental effects on changes in abundance.

A useful assessment tactic may be to work back and forth between mass balance and single species assessment methods using each to check and improve the other. To get further information on the functioning Ecopath, it is suggested the reader refers to Christensen et al. (2000).

References

Christensen, V., C. J. Walters & D. Pauly. 2000. Ecopath with Ecosim Version 4. Help System. Univ. British Columbia, Canada & ICLARM, Penang. (available at www.ecopath.org)

CMFRI. 2002. Trophic analysis of the fisheries along the southwest coast of India. Proc. ADB-RETA 5766 Project, ICLARM, Penang (in press).

Dayton, P. K. 1998. Reversals of the burden of proof in fisheries management. Science 279, 821-822.

Froese, R. 2001. Ten years of FishBase. EC Fish. Coop. Bull. 14, 13.

Froese, R. & D. Pauly. 2001. FishBase. (available at www.fishbase.org <http://www.fishbase.org>)

Mendoza, J. J. 1993. A preliminary biomass budget for the northeastern Venezuela shelf ecosystem. In V. Christensen & D. Pauly, eds. Trophic Models of Aquatic Ecosystems, pp. 285-297. ICLARM Conf. Proc. 26.

Pant, A. 1992. Primary productivity in coastal and offshore waters of India during southwest monsoons, 1987 and 1989. In B. N. Desai, ed. Oceanography of the Indian Ocean, pp. 81-90. New Delhi, Oxford & IBH Publ.

Pauly, D. 1993. Foreword. In R. J. H. Beverton & S. J. Holt, eds. On the Dynamics of Exploited Fish Populations, pp. 1-3. London, Chapman & Hall.

Pauly, D., V. Christensen & V. Sambilay. 1990. Some features of fish food consumption estimates used by ecosystem modelers. ICES Counc. Meet, 1990/G, 17, 8 pp.

Polovina, J. J. 1984. Model of a coral reef ecosystem. 1. Ecopath model and its application to French frigate shoals. Coral Reefs 3: 1-11.

Vivekanandan, E. 2001. Sustainable coastal fisheries for nutritional security. In T. J. Pandian, ed. Sustainable Indian Fisheries, pp. 19-42. New Delhi, National Academy of Agricultural Sciences.

Walsh, J. J. 1981. A carbon budget for overfishing off Peru. Nature 290: 300-304 pp.

Winberg, G. G. (1956). Rate of metabolism and food requirements of fishes. Trans. Fish. Res. Board Canada, 253 pp.

Fisheries management

A short note on fisheries management in South and Southeast Asia

Purwito Martosubroto
Fishery Resources Division
FAO Fisheries Department, Rome

Introduction

The development of fisheries in the region has led to an increase in the value of exports from the sector. The export value had increased from US $ 1.8 billion in 1976 to US $ 10 billion in 2000, that is more than tenfold in two and a half decades. On the other hand, this rapid development has led to overexploitation of the resources from which various consequences have emerged, the most common being conflict among fishers. Most countries in the region have introduced some management measures in response to the issues of overexploitation.

Generally these have not included controls on the magnitude of either the fishing efforts or annual catches. As such the overexploitation can be expected to increase further. Historically in the eyes of policy makers in some developing countries, the word "management" was not in their interest and some have shown a negative attitude towards taking management action, principally due to socio-political reasons.

There has been a gradual improvement, however, especially after the adoption of the Code of Conduct for Responsible Fisheries. The Code has become an important and useful guide to the principals of management, leading to an increasing number of countries becoming more open and inclusive of other stakeholders in respect to management. This is shown by the increasing number of requests for assistance in the context of implementing the Code.

Management measures

The common measures in the region include prohibition of fishing with destructive or harmful fishing gears, regulation of net mesh-sizes, closed seasons and closed areas, and zoning with regard to certain gears and fishing operations. Pressure in managing the fisheries has increased in recent years and weakness in law enforcement is one of the weaknesses in the region.

Yet, some success could be mentioned, such as the close-season scheme for the management of short mackerel in Thailand, and the ban on trawling in the western part of Indonesian waters.

To a limited extent there is also limitation on the number of fishing boats, particularly with regard to the commercial/industrial fisheries sub-sector. In reality, despite limits on the number of boats, in the absence of associated control of the other components of fishing effort (e.g. quantities and types of gear, number of fishing days, etc.), exploitation levels are not being controlled.

Another feature in the fisheries sector in the region is the relatively large number of fishers (some stricken with poverty) in the coastal area. Many of these have little or no possibility of alternative employment. It is within this context that in addressing the management of fisheries in the region, one should distinguish between small-scale fisheries and commercial/semi-industrial fisheries.

Community-based management

In respect to the small-scale fisheries sector, there is an increasing trend to address it in the context of community-based management. Experience is now accumulating, though still limited, in applying the concept to integrated coastal resources management. In this the scope is expanded beyond fisheries, to include assessing and managing the impacts from all the users of the coastal environments.

Such an approach has been promoted in the Philippines through generous technical assistance from donor countries, and some through loans from financial institutions such as the Asian Development Bank (ADB). This kind of initiative is currently taking place as well in Sri Lanka and Indonesia. A similar approach to community-based fisheries management had been conducted earlier in Phanga Bay with the financial support of the FAO/Bay of Bengal Programme.

Management plans

In an effort to strengthen fisheries management in the region, FAO has promoted the concept of fishery management plans. Case studies were undertaken in Indonesia, Malaysia and Thailand. The development of fisheries management plans is based on a process of consultation (and negotiation if necessary) amongst stakeholders. Through this, the agreed objectives, policies and strategies are identified, and subject to government approval, the resulting plan is empowered through legislation. Box 1 provides an example of the structure of a fisheries management plan.

Through this process and associated documentation, one is able to identify who will be responsible for what and how the overall process of managing the fisheries is to evolve. Realising the importance of fisheries management plans, some countries have accepted the legal commitment, and established the requirement for management plans in their fisheries legislation.

Fishery statistics

Information on the status and trends in fisheries provides a simple description of the sector at a particular development stage. Fisheries information can be readily accessed at the fishing ports. Proper administrative handling of statistics collections at fishing ports should be a priority to assure good statistics of catch and fishing vessel operations.

In line with this, the provision of information on fishing and its associated catch by fishing operators through the provision of log book data can also be facilitated at the fishing port (at least for commercial fisheries). The provision of such information can form one of the important conditions for the granting/renewal of fishing license by policy makers. Vessel operators failing to provide such information could have their fishing licenses cancelled.

The process of developing fishery management plans provides a good forum where fishery managers and other stakeholders can address together various issues of management. One would be able to identify the kind of information (including statistics and stock assessment) required for management. The plan itself might indicate the types of data to be collected in order to assess and monitor fishery performance, and possibly also the methodology of data analysis and interpretation.

Regional cooperation

Fish resources do not recognize administrative boundaries and move between countries to complete their live cycle. As such, some small-pelagic fish stocks are shared. Potential shared stocks were identified in various adjacent waters of the Malacca Straits and South China Sea in 1985.

Short mackerel (Rastrelliger spp.) forms a shared stock for Indonesia, Malaysia and Thailand in the Malacca Strait, and round scads (Decapterus spp.) for Indonesia and the Philippines in the Sulawesi Sea. Such shared stocks are also found in the Bay of Bengal between various countries of South Asia, and in the northern Arabian Sea between India and Pakistan.

In addressing the management of shared stocks, FAO/APFIC and SEAFDEC have called for cooperation among countries in the region. It seems, however, unless national management institutions in the respective countries are strengthened, such cooperation will not be well founded.

Concluding comments

The future of fisheries will be crucially dependent on the management of the sector. Various efforts are currently being made to develop indicators that will show the status and sustainability of fisheries. Such indicators will eventually be used widely to measure performance.

At the global level, there is an emerging trend towards ensuring sustainability through trade measures. In future, failure to meet an international standard could result in the rejection of exports by the importing countries. Fishery products may require labelling to indicate they are from suitably accredited sustainable fisheries. In this way consumers will be able to play an important indirect role in the matter of fisheries management.

Linking research and management through a fishery management plan

Michael Sanders
Fishery Consultant
Melbourne, Australia

Introduction

This paper concerns the concept of legally empowered fishery management plans. In the modern usuage these would be formulated in a highly consultative process involving all stakeholders. An important by-product will be the achievement of stronger linkages between research and management. The example situations provided are from experiences with an Australian fishery.

The first part of the paper deals with formalisation of the institutional linkages. The second part concerns fishery objectives and the means of achieving these through prescribing performance indicators, reference points, and trigger responses. The third part deals with the process of formulating a plan. In respect to these matters, input and participation by all stakeholder groups would be expected.

Formalising the institutional linkages

Management plans for individual fisheries are now a requirement under most fisheries legislation. In broad terms the purpose of a management plan is to specify policies and strategies for the management of the fishery on an ecologically sustainable basis having regard to the interests of the relevant stakeholder groups.

The latter may include commercial, traditional, recreational, and non-consumptive users of the resource. Other stakeholders will include the managers of the fishery, whose responsibilities will be as defined by legislation and government policy. They will in turn be highly dependent on advice from research.

This advice will generally relate to the state of the fish stocks, and the performance of the fishery in each of its ecological, economic, social, and governance dimensions. A well-drafted management plan will seek to formalise the linkages between research and management.

Example:

• The abalone fishery management plan for Victoria (Australia) demonstrates a formalisation of the linkage between research and management. This is within a process of co-management involving the major stakeholder groups.

• The stakeholder groups include the commercial divers and owners of abalone quota, abalone aquaculturists, recreational divers, indigenous Australians, as well as the relevant government agencies and non-government statutory bodies.

• The manager of the fishery is Fisheries Victoria, which administers the Fisheries Act, provides management services to the fishery, and management and policy advice to the Minister.

• Under the Act participation of resource users and the community in resource management is promoted by the establishment of a Fisheries Co-Management Council (FCC) and its Fishery Committees.

• Members of the FCC and the Abalone Fishery Committee (AFC) are appointed for their expertise and knowledge of fisheries generally in the former case, and the abalone fishery in the latter case.

• The functions of the AFC include advising the FCC on the management of the fishery, evaluating reports on the status of the stocks and the fishery, and to prepare recommendations on the total allowable catch (and minimum length) regimes to apply in the forthcoming year.

• The input to the AFC from research is facilitated by the Abalone Fishery Assessment Group (Abalone FAG). Its membership includes the scientists of the Marine and Freshwater Resources Institute (MAFRI), other scientists with special expertise (e.g. in fishery stock assessment), and representatives of FV and each of the other stakeholder groups.

• The functions are to improve the scientific input into stock assessment of the abalone fishery, interprete assessment outputs for utilisation in management, encourage direct stakeholder participation in the stock assessment process, provide a forum for planning future stock assessment and other research needs and priorities, and prepare fishery assessment reports and associated scientific advice.

• In respect to the annual provision of advice to the Minister on the TAC (and LML) for the commercial fishery the management plan identifies the following timetable:

• The AbaloneFAG meets to consider stock assessment output from the MAFRI stock assessment model and other sources during September/October.

• Stock assessment advice from the AbaloneFAG is finalised before the end of ovember and the outcomes are forwarded to the AFC.

• AFC sends its recommendations on TAC and LML combinations for the forthcoming season (commencing on April 1) to the Minister by December 31.

• The Minister consults with Seafood Industries Victoria (a statutory non-government organisation) during January/February.

• The Minister approves the final form of the Quota Order for the coming season, to be published in the Government Gazette during March, to be followed by the distribution of Quota Notices to quota owners.

(Source: DNRE, 2002)

Objectives, performance indicators, reference points, and trigger responses

These can be expected in a management plan. They provide the framework against which the performance of the fishery is measured. In respect to many of the components, the necessary information required by the managers will be from research.

The objectives would form an integrated package, with those concerned with ensuring sustainability of the resource and associated ecosystem having paramount importance. This is in the sense that if an appropriate stock abundance cannot be sustained, the performance in respect to all other objectives will be at risk.

Example:

Ecological Objectives

• Productive capacity of stocks sustained into the future at low level of risk.
• Ecosystem health not jeopardised by fishery practices.
• Management responsive to changes in ecosystem health.

Economic Objectives

• Opportunities for commercial production fully utilised.
• Economically efficient commercial production.
• Commercial production directly enhanced as through aquaculture.

Social Objectives

• Equitable assignment of productive capacity between commercial, traditional, recreational, and non-exploitive uses.

• Appropriate community return where there is commercial use of publicly owned resources and habitats.

Governance Objectives

• Management which is cost-effective and transparent.

• Recovery of the attributable costs of management, including research and compliance.

• Stakeholders and government fisheries administration sharing responsibility and involvement in management.

• Compliance targets for licensed sectors of the fishery achieved and monitored.

• Illegal activities prevented and targets for reduction of theft monitored and achieved.

(Source: DNRE, 2002)

Performance indicators are quantities to be measured in order to track the status of the fishery relevant to the objectives. Target reference points represent the status that management wishes to achieve. Trigger reference points indicate that the status may be unacceptable to the extent that immediate remedial action is required.

Example 1:

In respect to the fishery objective "Productive capacity of stocks sustained into the future at low level of risk".

• Performance indicator: mature biomass.

• Target reference point: mature biomass at 110 percent of biomass at MSY estimated with 70 percent confidence.

• Trigger reference point: mature biomass at 100 percent of biomass at MSY estimated with 70 percent confidence(lower limit).

Example 2:

In respect to the fishery objective "Ecosystem health not jeopardised by fishery practices".

• Performance indicator: indices of ecosystem health. (eg. Relative abundance of algal cover, predator and prey organisms).

• Target reference point: (not applicable).

• Trigger reference point: ecosystem health indices at 90 percent of average value of previous 3 years (lower limit).

Example 3:

In respect to the fishery objective "Recovery of attributable management costs".

• Performance indicator: attributable management costs.

• Target reference point: 100 percent of attributable costs (or other percent as defined by government policy).

• Trigger reference point: (not applicable).

(Source: DNRE, 2002)

Trigger responses are the required actions, as described in the management plan, in the event of a trigger reference point being reached.

Example:

Whenever a trigger reference point is reached the Minister will be notified. The Co-Management Fishery Committee will meet as a matter of urgency to determine its assessment and advice to the Minister. It will recommend one of the following actions:

• no immediate action taken but situation re-evaluated following observation of resource for another fishing year, or

• immediate and intense investigation to clarify situation prior to further decisions and action, or

• action taken which adjusts the total allowable catch (TAC) and/or legal minimum length (LML) for the immediately following years, with the objective of restoring the mature biomass to above the trigger reference point within five years, or- other actions as appropriate to achieve recovery from the trigger value with the minimum delay as practicable but not exceeding five years.

(Source: DNRE, 2002)

Process of formulating a management plan

A plan should fully address the requirement of the Fisheries Act and any Ministerial Guidelines. Its purpose will be to specify policies and strategies for the management of the fishery on an ecologically sustainable basis, and having regard to the well-being of each stakeholder group.

Example:

Stakeholder consultation

A working group to be established made up of representatives of the various stakeholder groups as endorsed by the Minister. The role of the group might be to:

• facilitate inputs by the stakeholder constituents into preparation of the plan,
• identify issues to be addressed in the plan,
• identify options (ie. policies and strategies) for resolving the issues,
• facilitate regular updates to stakeholder constituents on progress with the plan,
• provide comment on drafts of key documents including plan.
• endorse the final draft plan for Ministerial approval.

Role of DoF

In recognition of its legislated responsibilities the Department of Fisheries would be the client agency. Its role in respect to the preparation of the management plan might be to:

• ensure the requirements of the Act and Ministerial Guidelines are met,
• keep the working group appraised of relevant government policy,
• provide the Ministry and Minister with reports on progress,
• participate directly as a stakeholder entity in developing the plan.

Role of consultants

The expertise and experience of the consultant team would generally be to facilitate the writing of the plan. Its specific role might be to:

• oversee the process of developing the management plan,
• assist stakeholder input by jointly convening working group workshops,
• provide comment and guidance at the workshops,
• write the draft plan and associated documents (eg. issues/options paper),

Process and timing

The following envisages three workshops and associated pre- and post- workshop activities.

First workshop

• Membership of the working group including identification of its chairman to be decided prior to the workshop. These are to be determined by DoF.

• The workshop to take place over 2 days at a date and venue to be decided. Venue and accommodation is to be organised by DoF. In associated DoF to issue invitations to the chosen workshop participants. Invitations to be accompanied by prospectus and working documents as identified below.

• An issues paper, that provides an initial identification of the fishery management issues to be addressed and related background information, will be the principal working document. This to be written by the consultant team prior to the workshop.

• Other documents for use at the workshop to include management plans for like fisheries. The consultant team to provide these.

• Additional background to include a fishery status report (with current management, costs of management, and revenues from fees, levies and royalties). DoF to provide this.

• The objective of the workshop to be an initial documentation of the possible options for resolving each of the identified issues. The output would be an issues/options paper to be written by the consultant team immediately following the workshop. This to be available to the working group members within 3 weeks of the workshop.

• Choosing the preferred management option relevant to each issue would be the task of the second workshop.

Second workshop

• Membership and chairman of the working group expected to remain as previously, although subject to confirmation by DoF.

• Workshop to take place over 1 or 2 days and at a venue to be decided, possibly at the end of the first workshop, all subject to confirmation by DoF.

• The previously circulated issues/options paper to be the principal working document, following any editing that might be required. Editing would be undertaken prior to the workshop by the consultant team, based on comment received from working group members.

• The objective of the workshop would be a determination of the preferred options relevant to each of the management issues. This to be sought by consensus and in recognition of the possible need for compromise.

• The output to be a first draft plan to be written by the consultant team immediately following the workshop. This would be available to the working group members within 3 weeks of the workshop.

• Any unresolved contentious issues are to be flagged. Resolution of these and developing the final draft plan to be the task of the third workshop.

Third workshop

• Membership and chairman of the working group expected to remain as previously, although subject to confirmation by DoF.

• Workshop to take place over 1 or 2 days and at a venue to be decided, possibly during the previous workshop, all subject to confirmation by DoF.

• The previously circulated first draft plan to be the principal working document, following any editing that might be required. Editing would be undertaken prior to the workshop by the consultant team, based on comment received from working group members.

• The objective of the workshop to be the resolution of any contentious issues and the finalisation of the second draft plan. Again this would be sought by consensus. In the event that contentious issues cannot be resolved in this way an alternative process of resolution to be decided by the working group, subject to the agreement of DoF.

• The output to be the final draft plan. This to be written by the consultant team immediately following the workshop, and available to the working group members within 3 weeks of the workshop. Alterations to this scheduling might arise should further time be required to resolve contentious issues.

Submission of plan to the Minister

• The final draft plan following any editing arising from comments by the working group would be submitted to the Minister by DoF through its Ministry. Any associated advice from DoF to be as an accompaniment.

• These to reach the Minister in time to enable legal declaration of a management plan to be completed prior to the commencement of the next fishing season. Full implementation of the plan may require further time.

Concluding comments

Legally empowered fishery management plans do not presently exist within the region. This is despite most countries having the requirement for management plans written into their legislation. The pre-requisites are stakeholder groups appropriately organised and representative, adequate knowledge about the fisheries in question, and willingness by governments to make the hard decisions.

The many virtues of a plan are broadly that they clearly indicate the fishery objectives, how these objectives are expected to be achieved, and the respective responsibilities and roles of the various stakeholder groups. Both in their formulation and implementation, they ensure that stakeholders, managers, researchers and other are linked to a common purpose, the better performance of fisheries and community welfare.

References

DNRE. 2002. Victorian abalone fishery management plan. The State of Victoria, Department of Natural Resources and Environment, April 2002: 52 p.

Linking research and management through fishing community/industry/government co-funding

Michael Sanders
Fishery Consultant
Melbourne, Australia

Introduction

This paper concerns the co-funding of research and development (R&D). With reference to examples, it demonstrates that a useful by-product is better linkages between research and management. This would occur as the consequence of several factors.

Obviously when the fishing community and industry are contributing funds, they will closely monitor the expenditures to ensure appropriate focus and efficiency. Often, they will participate in the decisions about how the moneys are spent.

This would most likely occur within a co-management framework, with researchers, managers and other stakeholders working together.

The first part of the paper deals with concepts concerning the broad categories of funding, who should pay, and why. An underlying premise is that those who benefit should contribute, in proportion to the benefit to be received.

The second part borrows heavily from the experiences of the Fisheries Research and Development Corporation (FRDC) of Australia. It describes the functions, structure and processes; and in so doing provides an example of the linkages.

The final part provides another example, this time in respect to a small-scale fishery. In this a radical new co-management regime in association with R&D co-funding is described. The regime does not exist, but is presently under consideration.

Concepts to funding research and management

It is usual to consider three broad categories of funding to be collected from resource users. These are fees for services provided, levies in order to fund special purpose activities, and royalties in lieu of private use of public resources.

The context of the first is cost recovery. In the application of cost recovery it is necessary to distinguish between attributable and non-attributable costs. In respect to fisheries the former are those costs (to government) that would not exist in the absence of the fishery.

Issuance of fishing licenses, registration of boats, enforcement, and a proportion of the R&D costs might all be considered as attributable. Under a full cost recovery regime these costs would be recovered through the appropriate charging.

The funding source to meet non-attributable costs, as might be incurred in consequence of the stewardship role of government, would be the contributions to consolidated revenue from the general public. This could include costs of research that might have been required even in the absence of the fishery.

The presumption underlying the application of cost recovery is that a mature and well managed fishery should generate sufficient revenues to cover its own costs. The meeting of attributable costs from consolidated revenue would represent a subsidy.

The presumption underlying the application of royalties is that naturally occurring fish stocks are public property. Royalties have particular relevance where participation is restricted to a relatively small number of entities. Also in the special case of foreign fishing in EEZ waters.

An important pre-requisite to the charging of royalties is that the fishery is sufficiently profitable. This may not be the case if there is excess fishing capacity. In such circumstances governments should already be seeking some industry re-structuring in order to improve profit levels.

Cost recovery, special purpose levies, and royalties may be combined within a single charge. In such cases it would be important that the proportioning of the charge between each is clearly identified. Also the rationale for each should be clearly understood.

Further background to R&D levies

Levies are a charge on a sector component (e.g. fishers, processors, exporters) in order to fund activities beneficial to the sector. R&D levies are the most common form applying in the case of fisheries.

Payment is typically proportional to the magnitude of the production, but may be a flat fee applying to all participants. An advantage is that they make funding more dependable, although this is not absolute as funding linked to production would decline significantly in the event of fishery collapse.

Also advantageous is the likelihood that contributors will have some control over the spending of the levies. This tends to ensure that the expenditures are demand-driven and there is more direct accountability to contributors.

Often the expenditure of levies is through private entities. This is especially useful in countries where the public service suffers greatly from inadequate/unreliable funding, low wages, bureaucratic decision making, and poor incentive structures.

Also a sector contributing its own money may achieve added benefit by mobilising other funds, as when there is a matching contribution into a levy fund by government. Conversely, a decision to provide matching funds can act as a useful incentive to industry contributions.

Matching funds from government can be justified in the context of the 'inseparability' of private and public benefits. The proportion of public good (e.g. employment, foreign currency) flowing from a well functioning fishery is high.

In respect to the administration of levy-funded activities, one option is to have semi-public organisations or statutory bodies to undertake both the allocation of funds and the execution of funded projects. The more normal alternative is to separate allocation from execution.

The latter can be achieved by having a statutory funding body that allocates the revenues from a levy to existing public and/or private executing entities on a competitive basis.

Example:

a. The Fisheries Research and Development Corporation (FRDC) of Australia administers levy funds from the following sources:

• the Commonwealth Government providing unmatched funds equivalent to 0.5 percent of the average gross value of Australian fisheries production for the three preceding years (Australian Gross Value of Production, AGVP);

• state, territory and commonwealth fishers and aquaculturists providing contributions of at least 0.25 percent of AGVP;

• the Commonwealth Government matching contributions by state, territory and commonwealth fishers and aquaculturists up to a maximum of 0.25 percent of AGVP.

b. The FRDC does not undertake research itself, nor is it a research grant agency. Rather the enabling legislation requires it treat R&D as an investment in economic, environmental and social benefits to the respective fishing communities and to the population at large. It is empowered to intervene anywhere in the innovation process.

c. This is reflected by its mission statement "to increase the social and economic benefits for the fishing communities and other industry stakeholders, in a manner that seeks that the benefits are sustainable, and with minimum cost to the ecosystem".

d. The associated functions of the FRDC are as follows:

• investigate and evaluate the requirements for fisheries research and development and, on that basis, prepare a five-year R&D plan, review it annually and revise it as required;

• prepare an annual operational plan for each financial year;

• coordinate or fund the carrying out of R&D activities that are consistent with the annual operational plan;

• monitor, evaluate and report to the Parliament, the Minister or Parliamentary Secretary, the Australian Seafood Industry Council and the Australian Recreational and Sport Fishing Industry Confederation on R&D activities that are funded; and

• facilitate the dissemination, adoption and commercialisation of the results of fisheries R&D.

e. The statutory powers allow the FRDC to do all things necessary or convenient to be done for, or in connection with, the performance of its functions, which may include:

• entering into agreements for the carrying-out of R&D activities by other persons;

• entering into agreements for the carrying-out of R&D activities by the FRDC and other persons;

• making applications, including joint applications, for patents;

• dealing with patents vested in the FRDC and other persons;

• making charges for work done, services rendered, and goods and information supplied by it;

• accepting gifts, grants, bequests and devices made to it, and acting as trustee of money and other property vested in it on trust;

• acquiring, holding and disposing of real and personal property;

• joining in the formation of a company; and

• doing anything incidental to any of its powers.

f. The Board of the FRDC are selected in accordance with the Act as follows:

• The chair and the Government Director are selected and appointed by the Minister or Parliamentary Secretary.

• The Executive Director is appointed by the Board on terms and conditions determined by the Board.

• The other six directors are appointed by the Minister or Parliamentary Secretary on the nomination of a selection committee. The Minister appoints the selection committee based on the nominations of the representative organisations.

g. Directors are appointed for a term not exceeding three years, except for the Government Director, who holds office at the Minister's pleasure, and the Executive Director, who holds office at the Board's pleasure. All directors other than the Executive Director are appointed on a part-time basis. The selection of directors is on the basis of their expertise in one or more of the following fields:

• commodity production,
• commodity processing,
• marketing,
• conservation of natural resources,
• management of natural resources,
• science,
• technology and technology transfer,
• environmental and ecological matters
• economics,
• administration of research and development,
• finance,
• business management,
• sociology, and
• government policy and public administration.

h. There are two representative organisations; the Australian Seafood Industry Council and the Australian Recreational and Sport Fishing Industry Confederation. These are identified through a notice published in the Government Gazette, as being representative of the fishing community and industry stakeholders. They are required to be consulted when preparing and seeking variation to a five-year plan or annual operational plan.

i. Targets for funds expenditure are set by Ministerial Direction. The current profile of expenditure by the FRDC is as follows:

• R&D projects: minimum 85 percent,
• communications: minimum 3 percent, and
• support: maximum 8 percent.

Communications includes production of R&D plans, annual report to parliament, dissemination of R&D results, and technology transfer. Support includes remuneration to directors, staff appointments, rental accommodation, project evaluation, monitoring, commissioning, tendering, and other administration.

j. The R&D projects are grouped into three approved programs with planned outcomes and proportions of the R&D budget as indicated:

Program 1: Natural Resources Sustainability:

The natural resources on which the fishing communities, and other stakeholder participants depend are used in a sustainable way.

[60 percent]

Program 2: Industry Development:

The commercial sector of the fishing industry is profitable and internationally competitive; and all sectors are socially and economically resilient.

[35 percent]

Program 3: Human Capital Development:

The knowledge and skills of people in and supporting fisheries, and the wider community, are developed and used to derive maximum economic, environmental and social benefit.

[5 percent]

k. The FRDC supports a network of Fisheries Research Advisory Boards (FRAB). They exist for each major commonwealth fishery, and are extremely important in maximising the efficiency of the FRDCs planning and funding process. Their role in respect to the particular fishery is to:

• set R&D priorities to maximise investment, and achieve greatest potential benefit,

• develop strategic plans for R&D,

• invite R&D applications to address these priorities,

• encourage collaboration between researchers, and between researchers, fisheries managers and other stakeholders,

• identify appropriate funding sources (including the FRDC),

• advise the FRDC on the priority and appropriateness of applications for funding,

• assist the FRDC with communication and extension of R&D results.

The FRDC meets some of the costs of operating the FRABs. It is not the sole beneficiary of their outputs: other beneficiaries include fisheries management agencies, other research funding agencies, research providers and industry.

In evaluating prospective R&D projects for funding the FRDC applies comprehensive criteria. These are as follows:

Attractiveness

• Is the application relevant to the FRDCs R&D programs?

• Is the need well-defined and relevant to R&D priorities that are documented in strategic plans for R&D produced by FRABs and/or other entities?

• Is the application supported by the appropriate FRAB(s), industry sector(s), fisheries management agency/agencies, and other potential beneficiaries?

• Are the planned outcomes well quantified and qualified, and will they meet the defined need?

• Is the applicant, potential beneficiary or other entity making an appropriate financial contribution to the project?

• Will the planned outcomes, if achieved, contribute to resolving market, institutional or political failure, or will they act in the public good?

• Will the planned outcome, if achieved, provide a high benefit-cost ratio or a sound return on investment or value for money?

• Does the potential industry beneficiary contribute financially to the FRDC?

• Is there an appropriate level of collaboration between researchers, and between researchers, fisheries managers and fishing industry interests?

• Is the project original? Does it add value to previous R&D?

Feasibility

• Are the planned project outputs well described, and is the strategy for extending the outputs sufficient to achieve the planned outcomes?

• Are the objectives clearly specified, and are they consistent with planned project outputs?

• Are the methods well described, and are they consistent with the project's stated objectives?

• Does the applicant have the capacity and commitment to produce the planned outputs?

• Are the principal investigator and other researchers to be engaged on the project competent? Have they performed well in the past?

Other considerations

• Is there a strategy for managing data arising from the project so that it will be easily accessible to others in the future?

• Will project outputs contribute to future R&D?

• Will the research have an impact on endangered, rare or sensitive ecosystems?

• Will the research have animal welfare impacts?

• Will the research require some sort of external approval because of its impact on ecosystems or animal welfare?

m. The R&D projects are managed through a range of mechanisms. This includes an in-house computerised project monitoring system, that integrates technical, financial and administrative data. Projects are formally required to report against progress with achieving milestones stated in the project agreement. FRDC staff technically evaluates milestone reports, where necessary assisted by technical advisors. The staff also undertakes on-site audits of financial management, and compliance with contract conditions.

n. All completed projects are subject to a low-cost impact analysis, based in part on post-evaluation questionnaires to determine the project benefits. More rigorous benefit -cost analysis is applied to a small number of projects most suited to the methodology.

Source: FRDC website <www.frdc.com.Au>

R&D levies applied to a small-scale fishery

The ability to achieve fishing community contributions to meeting R&D costs will be constrained by prevailing levels of profit. Often in small-scale fisheries there is insufficient profit, in which case government or other industry sector (e.g. fish processors, exporters) must meet these costs, until profitability can be restored.

Changed management arrangements may provide a useful opportunity to implement an associated R&D levy scheme. The linkage is obvious in the sense that any collection of levy funds will not be sustainable unless the fishery performance itself is sustainable.

Example:

a. A proposal for management of the Kenyan component of the Lake Victoria Nile perch fishery is linked to the application of an R&D levy (MENR, 2002). Here there are some 38,000 fishermen operating 11. 5 thousand craft. Landings are in the order of 200,000 t of which about 45 percent are Nile perch. The latter are substantially over-exploited.

b. The proposal envisages the determination of a Lake Victoria TAC, and its allocation between Kenya, Tanzania and Uganda. Re-allocation between countries would be at the sole discretion of the countries concerned.

c. In respect to the Kenya TAC it is proposed that this be re-allocated first between districts, then between beach management units (BMUs) in each district, and then between the boat owners at each beach. There are BMUs established at each of 297 designated beaches.

d. At the first two levels there would be co-management entities to determine the re-allocations. Allocations at the third level would be at the sole discretion of the BMUs. Each BMU would be expected to establish an appeals process in the event of dispute concerning Boat TAC allocations.

e. BMUs are mostly comprised of 5 to 9 persons chosen to be representative of the fishermen at the beach in question. Presently they resolve disputes, organise/coordinate safety and emergency procedures, and seek to improve beach infrastructure, sanitation and hygiene. Any expenses incurred are levied directly from the fishermen.

f. The proposal envisages a substantial expansion of the functions for BMUs. Presently fishing licence and boat registration fees are collected by district fisheries officers. It is proposed that these be collected in future by BMUs. The incentive would be a 30 percent discount on the full charge fees. Where a BMU chose not to collect, fisheries officers would do this as at present.

g. A second additional function relates to achieving compliance with TAC allocations. The proposal is for the BMUs to be responsible for the weighing of catches and the maintenance of suitable records, against which compliance can be determined. The incentive being offered here is a further 40 percent discount on the fishing licence and boat registration fees.

h. Another implied incentive concerns achieving adequate levels of compliance. This is in the sense that if Beach TACs are substantially exceeded there is the risk of reduced TAC allocations in future years. The fishing communities would most keenly feel the effects of continuing fishery decline, and as such it is reasonable that they play a major role in the process of achieving compliance.

i. All Boat TAC allocations would be in respect to a single year, with no 'right' to allocation in subsequent years. This would be clearly reflected in law, and have the effect of preventing any notion of trading (to buy, sell or lease) the allocations of future years.

j. The proposal does not seek to prevent the trading of allocations within a year. The ability to transfer an allocation, subject to the agreement of the associated BMU and the adjustment of records, could be desirable in enabling flexible arrangements between boat owners.

k. In addition to these measures aimed at improving the management of the fishery, the proposal also envisages new arrangements in respect to the funding of R&D. There would be R&D levies charged against both the boat owners and the exporters (of Nile perch fillets).

l. The levy on boat owners would be a Kshs/kg amount applied to the Beach TACs. As a third additional function the BMUs would be responsible for collecting the levies, with the lump sum amounts remitted to the district fisheries offices immediately prior to the fishing season. These in turn would be remitted through district commissioners to a Lake Victoria Fish Levy Trust Fund (LVFLTF).

m. In respect to the exporters, the present fish export fee would be increased, and an amount matching the levy contribution from boat owners would also be lodged in the LVFLTF. The fee is as a percentage of the export value. The process of collection, which involves fisheries officers, would be continued.

n. A Lake Victoria Fish Levy Management Trust (LVFLMT) would be established to administer the allocation of moneys from the fund. It would not of itself undertake R&D, but rather it would be responsible to its stakeholders for:

• assessment and approval of applications for funds in recognition of the legislated objectives;

• planning, funding and managing funds expenditure on approved projects; and

• facilitating dissemination and commercialisation of results from funded R&D projects.

o. Other aspects of the proposal are similar to those of the FRDC of Australia (see earlier sections).

Concluding comment

Present arrangements concerning the funding of R&D in the region are poor. There is over-reliance on funding from external sources, particularly through international and bilateral aid organisations. This funding cannot be considered sustainable, and is already become less available than in the past.

In several ways outside funding is counter-productive. In a sense it is a subsidy. It has the effect of encouraging exploitation levels greater than would be otherwise. Also, when the funding is from outside, there is a lesser commitment on local stakeholders to ensure effective use of the moneys.

Amongst the many hard decisions required of the managers, securing adequate and sustainable local funding for R&D must become a priority. As fisheries become better managed, it should become easier to convince fishing community and industry stakeholders to contribute financially to their own welfare.

References

MENR (2002). A study leading to the establishment of Fish Levy Trust. Workshop discussion paper. Ministry of Environment and Natural Resources (Kenya). July 2002: 51 p.