Alejandro A. Anganuzzi1
Inter-American Tropical Tuna Commission
8604 La Jolla Shores Drive
La Jolla, California 92037 USA
1 Current Address: Indo-Pacific Tuna Programme, P.O. Box 2004, c/o NARA, Crow Island, Mattakkuliya, Colombo 15, Sri Lanka.
ABSTRACT
Technical approaches for studying fishery interactions are discussed. The specific approach in each case depends on the nature of the interaction. Generally, a longer distance (in space or time) between potentially interacting fisheries means a more difficult identification of significant effects. A two-stage strategy is offered as a way of approaching the problem. In the first stage, a conceptual model of how the interaction occurs leads to a refinement of the hypotheses and to the identification of relevant information needed. In the second stage, options for management action need to be formulated according to the immediate objectives. Such objectives might include obtaining better information on the nature of the interaction. Methods for assessing interactions that use data from tagging experiments offer the best chance of providing conclusive evidence of an interaction, as well as quantifying its extent, in a relatively short period of time. Such an experiment can be successful, however, only if there is a reinforcement of the statistical systems in the fisheries involved.
1. INTRODUCTION
Interactions between fisheries exploiting the same resource are a growing problem in fisheries throughout the world. In some regions, resources are being exploited by heterogeneous fleets operating over vast areas, often covering the exclusive economic zones (EEZs) of several nations. Almost inevitably, this will lead to controversies among users of the resources about the extent of the interactions and about the best way to manage the exploitation of the resources.
Our role as scientists is to provide some of the elements that managers will need in order to resolve these potential conflicts. To provide this advice, we rely upon a collection of techniques that can prove valuable to characterise fisheries interactions, provided that we have the data. The objective of this paper is to discuss some of the problems that we will face, together with the technical strategies that we could follow. This review is intended as a starting point for discussion rather than a definitive document, and, in its final version, will incorporate the results of the discussion during the Second FAO Expert Consultation on Interactions of Pacific Tuna Fisheries.
Before beginning with the review, we need to establish an agreement about how we define and characterise interactions. Therefore, in the next section we will review some of the definitions and classifications of interactions that have been proposed.
As is the case with most management problems related with the exploitation of natural resources, we are faced with a two-stage problem in studying interactions. In the first stage, we need to identify and characterise the problem. That is, we need to formulate a model of how the interaction is operating; and provide values for the parameters that are relevant for the interaction. In a second stage, we must explore alternative management strategies, which means providing managers with a clear view of the trade-offs among the available alternatives; the trade-off is a sensitive matter since different objectives might translate into very different policies being preferred. The second section of this review expands on these themes. The remaining sections discuss the technical approaches that we can apply to the study of interactions, keeping in mind the dual aspect of the problem.
2. THE PROBLEM: WHERE DEFINITIONS ARE REVISITED
As a result of the First Consultation, several definitions of the interaction problems were proposed. The basic concept is that the activities of one (or more) fishery might affect the performance of some other fishery (or fisheries). In order to simplify the examples, I will consider the case of just two fisheries interacting: fisheries A and B. The definition of fishery must be left intentionally vague since, in practice, it will be situation-specific and depend upon the perception of conflicting interests between sectors of the overall fishing fleet. For example, two interacting fisheries could be different gears operating on the same resource or simply two different sectors of the same fishing fleet that differ in where and when they prefer to capture the fish.
Having agreed upon a definition of interaction, we can recognise many different formats and classifications based on the characteristics of the underlying process. Perhaps the first distinction to make is between resource-mediated and direct interactions (Kleiber, 1994). Resource-mediated interactions occur when two or more fisheries exploit the same resource, whether at the same stage in their life-history or not. We can extend that basic definition to include the case where fishery A exploits a species that provides forage for species B. Resource-mediated interactions will be most difficult to assess, since in many cases, this requires more information about the processes related to the resource (primarily in the dynamics of the population) than is currently available. In a typical scenario, an interaction between two fisheries would be suspected if changes in the performance of one fishery are correlated with the activities of the other fishery. Obviously, it will not suffice simply to say that there is an interaction between those two fisheries. We need to assess the level of the interaction. Furthermore, we would like to know the mechanisms leading to the interaction, since we can postulate alternative hypotheses to explain the trends observed in the data.
The second category involves direct physical interference between gears, a definition that perhaps could be extended to include interference between the fishery and other economic activities, such as industrial or recreational uses of the environment. These are not going to be discussed any further in this review, primarily because direct interactions do not pose special estimation problems: if two gears interact directly we can almost always set up experiments with the purpose of measuring directly the interaction.
Kleiber(1994) also makes a distinction between absolute and marginal interactions. Absolute interaction refers to the absolute effect that fishery A has on fishery B, while marginal interaction refers to the effect that a unit increase in the activity of fishery A will have on fishery B. Kleiber(1994) discusses some of the issues that arise when considering these different types of interaction.
In another document, also presented at the First Consultation, Hampton (1994) proposed the following classification of fishery interactions:
· Type A: Competition for fish at the same stage in their life cycle in the same general area by two or more fisheries;Other distinctions could possibly be based on the symmetry of the interactions. For example, Type A and some Type C interactions can be thought as symmetric, since both fisheries A and B may affect each other’s performance. In Type B, usually the early fishery affects the outcome of the fishery exploiting the later life stages (although this depends on the dynamics of recruitment). Considering the symmetry of the interactions leads us to some problems about the stability of both fisheries that are not unlike certain problems in predator-prey systems.· Type B: The effects of fishing a stock at an early stage in its life cycle upon a fishery that exploits the stock at a later stage, typically with a different gear; and
· Type C: The effect of fishing a stock in one area upon a fishery that exploits the stock elsewhere.
We can exemplify some of the main problems with estimating the level of interactions using the simplified situation where we have two fisheries: A and B, exploiting the same resource. The fish are initially available to fishery A, then the survivors move and become available to fishery B. In that simplified situation, the main number that we are interested in is a conditional probability: the probability that a fish caught by fishery A would have been caught by fishery B. If we denote this probability by P(Cb), we can consider a simple representation of the main processes:
 (1)
(1)
This is a product of three components:
1) mab : The proportion of fish that would have left area A in the direction of area B, except that they were caught in area A,Therefore, we can assess the level of interaction by estimating the number of fish that would have been caught by fishery B (in the absence of fishery A), as2)
The fraction surviving the trip from area A to area B (
M represents the instantaneous natural mortality and tab is the transit time between areas A and B; and
3)
: The fraction of fish that are caught in area B, where Fb and Mb are the instantaneous fishing and natural mortality rates in area B.
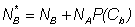 (2)
(2)
This simple approximation illustrates some of the main problems that we need to face. First, it is clear from equation 1 that the level of interaction is a function of the exploitation level of fishery B. However, it also depends on the exploitation rate of fishery A (through NA). Obviously, the migration rate is another critical component; for fishery A, the exploitation rate depends on the residence time, which is a direct function of the migration rates. An interesting feature is that if a population exhibits density-dependent migration rates, the overall level of interaction would be underestimated by a model that assumes density-independent movement (that is, an assumed per capita migration rate could actually increase if densities were allowed to increase in area A). The migration rate and the factor representing survival during the transit between areas A and B, also control the degree of coupling between the two fisheries. Assuming density-independent effects (for example, in the natural mortality rate during the passage from fishery A to B) will bias our perception about the effect of fishery A, if natural mortality is actually density-dependent. Knowledge of the variability of this stochastic process is important to assess the strength of the interaction and to interpret possible correlations between the outputs of both fisheries. Note also that the migration rate, in this simplified scenario, is not necessarily a movement of individuals through space; it might be that they simply become less vulnerable to gear A (and more to gear B) as they grow.
This simple example represents a one-way interaction, namely fishery A affecting the outcome of fishery B. In a more common scenario, there will be also a similar set of processes representing the way fishery B affects the output of fishery A. For example, both fisheries might operate at different places of a migratory “circuit” of the population. This leads to the need for consideration of long-term effects of the interaction. If density-dependent effects on population growth are strong, the apparent depressing effect of the catches of fishery A might turn out to increase the long-term average yield of the population (if currently underexploited), although perhaps at the expense of yields obtained by fishery B. Similar situations must be considered from a yield-per-recruit point of view: changing the age-at-entry (by allowing a fishery that targets smaller fish) might increase the overall yield-per-recruit (for both fisheries combined).
All these considerations are compounded by the socio-economic side of the fishery. Size-related differences in price per unit weight and the way the revenues of the fishery are distributed are important considerations when fisheries of different scale are involved (e.g.: artisanal versus industrial fleets).
The classifications and characteristics of interactions discussed above are all based on interactions of several fisheries based upon a single stock. Interactions mediated through trophic relationships (where fishery A exploits the forage base for the target species of fishery B) have not been widely considered, although they have been often discussed in the context of multispecies fisheries and implicitly incorporated in such models. This class of interactions will not be discussed any further in this review: although in principle they might be important. The dynamics of forage species is a problem that adds another layer of complexity, and very few fisheries, have been studied closely enough to correctly specify the underlying processes.
If we consider the classification proposed by Hampton (1994), we notice that the level of interaction is going to be controlled by different sets of variables depending on the type of interaction. In other words, the relevant questions are different in each case. For example, knowledge of the migration rates is not as relevant in the case of a Type A as in Type C interactions. Therefore, knowing the type of interaction allows us to organise our data requirements.
3. A BASIC SET OF STRATEGIES
Suppose that we have been advised of a potential interaction for which we have little prior information. How could we proceed? As suggested in the Introduction, we can identify a two-stage strategy to follow:
1. Set up a conceptual model of the interaction by identifying the interacting components in the fishery and formulate a model of how the interaction is occurring. In some cases, this phase might be the easiest. For example, in a Type A interaction, where the competing fisheries are coincidental in space and time, there will be a much better chance to identify the mechanisms of the interaction than in a Type C interaction.The first phase is the one most likely to involve scientists directly, but both stages are obviously related. The identification of an interaction is relevant even if the situation is not such that we can do something about it. Proper management of even a subset of fisheries on a resource requires knowledge about the levels and impacts of all fisheries.2. Formulate a management plan that incorporates explicitly the interactions, considering alternative objectives. Here, we should discriminate between allocation problems and management of the overall resource.
4. STAGE ONE: SETTING A CONCEPTUAL MODEL
4.1 Identifying the Interaction
The natural first step in the analysis of any potential interaction is to construct at least a conceptual model of what mechanisms are behind it. In some instances, this will be a trivial exercise, as would be in the case of two fisheries coinciding in time and space in the exploitation of a common resource. Other situations, however, will prove to be more complex, with the need for the incorporation of time lags, specific migration timings and routes and even uncertain stock structures. In all cases, the exercise will be valuable from the point of view of forcing us to postulate explicit hypotheses that could explain the data. This is the key element, since in most of those more complex situations we will need to expand our data collection capabilities. Formulating models (at least conceptual models) facilitates the identification of the voids in the available evidence.
If we go back again to our classification of the types of interaction, we see that a Type A interaction poses little problem. That scenario can be well represented by a simple model where the population suffers fishing mortality from two independent sources. In this case, provided that the gear selectivities are similar, we may not even need an age-specific representation. Unfortunately, real life rarely is so simple.
There are several useful ways of analysing catch and effort data to document the existence and level of fisheries interactions. Beginning with the simplest cases, the empirical analysis of series of CPUE data may be useful to some extent (see, for example, Boggs, 1994). We need to emphasise, however, that the analysis of CPUE series has to be done in the spirit of an exploratory analysis and that the prospect of actually quantifying the interaction using just catch and effort data is not good in most cases. The problems with this kind of data for assessing an interaction are multiple. A common first step with CPUE data is to see whether or not CPUE in one area is correlated with CPUE in another area, which could suggest that the same fish are present in both areas. Unfortunately, in many cases, we would be constrained to use short time series with the undesirable consequence of a low statistical power for hypothesis testing, i.e.: it is unlikely that we will be able to detect anything but the strongest interactions. Note also that a correlation measure would not represent a measure of the strength of the interaction, but merely the degree of “commonness” of stocks exploited by the two fisheries. The situation is only aggravated if, prior to the correlation analysis, we have problems in finding the appropriate transformations to improve upon the distributional properties of the CPUE data. Moving to more robust, non-parametric approaches will only make matters worse in terms of the power of the tests. A second problem is that, even if we have tests with adequate power for some data set, the analysis may be affected by confounding factors.
Improvements can be made to simple correlation analyses if we can take some of the confounding factors into account by modeling the CPUE of fishery B as a function of effort in fishery A and a number of other factors that could be related to availability and catchability, e.g., factors affecting fishing power and environmental variables. In other words, we would be standardising the CPUE series in relation to possible exogenous factors. Generalised linear models are a specific technique with flexibility to accommodate different structural assumptions. In such a model, we can include the activity of fishery A (defined as either catch or effort) as an explanatory variable along with other factors that may affect the performance of fishery B, and test the significance of the each factor. Different time lags can also be tested if appropriate. Ideally, we would also want to incorporate the level of exploitation of the resource. It is widely recognised that the level of interaction is dependent on the overall exploitation rate of the population. The rationale is that the competition between different sources of mortality increases as the fishing mortality becomes the most important source of mortality in the population. Assessing the level of exploitation should therefore be one of the priorities in an initial assessment of an interaction. However, to be able to carry out this analysis, we need a specific set of data that is not always available from the fishery.
We would also want to test for significant statistical interactions in the effect of those factors (i.e., exploitation level and the activity of fishery A). If information is available, we can stratify the data more finely and test for significant statistical interactions in the effects of area-specific levels of activity of fishery A. The disadvantage of this approach is that it is more demanding in terms of data related to the operating characteristics of the fishery and information on the environment at the appropriate time and space scales.
The main problem with any linear modeling approach is that we can never be certain that we have incorporated all the variables that are relevant. Catch, effort and environmental databases with the information and resolution needed are frequently not available. The bottom line is that, unless the data show substantial contrasts in the potential causal factors (i.e., the environment, the activity of fishery A, etc.), we might not be able to discriminate between an environmentally- and fishery-driven trend in fishery B.
The variability of the catch process could be such that it would mask a weak coupling between two fisheries. Therefore, we need to bring in any auxiliary information that could provide information regarding the hypothesised interaction. The latter might come in the form of biological studies about the structure of the stock. Consider the example of two fleets fishing in two discrete time-area strata. The first question that we would like to answer is whether they are actually exploiting the same resource, in the sense that the productivity of the resource in one time-area stratum is linked to the productivity of the resource at the other time-area stratum. The relevant question is: How strong is the coupling between the two areas? That leads us naturally to the question of stock structure, and the techniques currently available to deal with this problem are later discussed.
4.2 Additional Data: Catch-At-Age or Catch-At-Size Information
If catch-at-size or catch-at-age information is available a more realistic analysis of fishery interactions could be achieved. In these circumstances, we can reconstruct the history of the population using a sequential analysis (VPA). If it is possible to reduce the number of parameters, by assuming separability of the fishing mortality or by including indices of abundance for specific groups of ages, we can expand upon the basic VPA and have an analysis with a true error structure. We can even include a specific parameter for interaction and test the significance of the parameter if we can cast the error structure in terms of a likelihood (see, for example, Porch et al., 1994; Punt and Butterworth, 1995). In most cases, however, the parameter estimation will be complicated by the absence of enough contrast in the data or by confounding between factors. For example, natural mortality and movement will be confounded and before we can discriminate between them, we need to incorporate more structural assumptions. This can be done by incorporating a specific assumption about the nature of the interaction and by comparing with a base case where no interactions are assumed. One problem is that, in general, recruitments are not going to be known. In order to be able to better identify the level of interaction, additional information will be needed. This is why, in most cases, tagging data is the best solution for the study of interactions.
4.3 Our Best Chance: Using Tagging Data
A tagging experiment may be a risky enterprise--it is usually expensive, and the possibility that it would not provide enough information to discard some of the hypotheses proposed is high. The design and amount of effort (in terms of number of tagged animals released) will determine the success of the experiment. The analysis of tagging data incorporates some new uncertainties but we can probably tackle most of them. Reporting rates are the most difficult parameter to estimate. Double tagging can be use to estimate tag shedding and, in certain situations, tag seeding can be used to assess reporting rates. Multiple releases in different areas and season can address spatial and temporal variability. Provided that these problems are solved, tagging data can be used as a way to assess exploitation rate, migration rates and potential interactions without having to collect long time-series of fishery data. Therefore, it is not surprising that this has been the preferred area of development of analytical methods. Perhaps the most serious limitation of tagging is that it does not address sources of recruitment and variability of recruitment because we cannot (at least, not yet) tag eggs and larvae.
Several approaches can be found in the recent literature, most of them well represented in the First Consultation. Majkowski et al. (1988) and Hearn and Mazanov (1996) proposed some interesting techniques that do not require a measure of the effort or detailed catch statistics in each fishery and that provide a direct measure of the level of interaction. To some extent, the efficiency of both methods depend on the possibility of re-releasing fish. Unfortunately, the possibility of capturing and re-release tagged fish without seriously affecting their chances of survival is very low, because of the way fish are usually handled during the commercial operations, the primary source of capture.
There is now an extensive literature on analytical tools that can be used to estimate movement rates and residence times from tagging data. Ishii’s (1979) work set the basic principles for combining simulation models and tagging data to estimate survival and movement rates. Sibert (1984) presented a two-fishery model that illustrates the basic application for the study of fishery interactions. Hilborn (1990) proposed an estimation procedure in the analysis of tagging data that, being based on maximum likelihood, allows for direct comparisons of nested models. These principles have been expanded in more recent work. Deriso et al. (1991) proposed a model that can provide area-specific estimates of movement rates and residence times. Lebreton et al. (1992) proposed a general approach to model selection and hypotheses testing in models that are not nested based on the Akaike’s information criterion. Anganuzzi et al. (1994) illustrated an application of the approach to estimate movement rates and gear selectivity. Some models represent movement as a combination of advective and diffusive processes. Sibert and Fournier’s (1994) model represents movement as two-dimensional advection-diffusion processes that are controlled by area- and season-specific parameters. Kleiber and Fonteneau (1994) presented a similar model based on one-dimensional movement. Salvadó (1994) proposed an extension to continuous cases by representing the transition probability densities through Green functions. Mullen (1996) estimated area- and time-specific diffusion rates by comparing consecutive spatial distributions in abundance.
However, in spite of the different philosophies behind each of the methods, the basic problem in the analysis of tagging data remains the same: accounting for the tags that were not recovered.
4.4 Accounting for the Missing Tags
In any analysis of tagging data, we estimate the probability of recovering a tag, as a function of various processes, some of which will be of primary interest to us since they relate directly to the quantification of interactions. In the models, we have several ways of representing the losses of tags. Generally speaking, we can assume that the loss of tags is due to two kinds of processes:
1) Type-I loss: a one-time event, in the sense that we assume that a certain proportion of the tags are lost shortly after being released or after the fish are caught. A number of processes can be postulated that might contribute to this loss. For example, the losses that occur shortly after tagging might be due to shedding of those tags that were not properly attached, or to mortality of the fish due to improper handling. The reasons for tags not recovered after the capture of the fish might be multiple (e.g., tagged fish are not noticed, tags might get lost during handling of the fish, or in the mail), but we pool them all under the category of reporting rate.Some of the Type-I losses are amenable to estimation: double tagging experiments are particularly useful to estimate tag-shedding rates. However, when these are not available, all sources of Type-I loss will be confounded and it will be almost impossible to discriminate among them, unless we are willing to make some restrictive assumptions.2) Type-II loss: a constant rate of attrition of the tags from the population. Tag-shedding might continue throughout the life of the tagged population. But tags also disappear from the population due to natural mortality and emigration (either permanently or temporarily) from the exploitable population (i.e.: they are no longer available to the fishery).
The estimation of reporting rates is the most difficult issue, because of the multiple sources of error. For the specific case of the study of interactions, perhaps the question of estimating an absolute level of reporting is not critical, since we can estimate the level of interaction from the relative recoveries in fishery A and B, provided that we have an estimate of fishing mortality which was obtained independently from the tagging study. However, to do so we need to know (or assume) something about the relative levels of the reporting rates, i.e., what is the reporting rate in fishery A relative to the reporting rate of fishery B (NRC, 1994).
The key point here is that our perception of the level of interaction will be conditional on our assumptions about recovery rates. The problem is that there is little that we can do about it. To some extent, large rewards for recovered tags will improve the chances of the tag being reported. However, many of the tags are perhaps never seen, because the time for inspecting the fish is very short or because the tags might be detached and lost during the handling of the catch. If most of the recoveries of tags occur when the fish are processed, tag seeding experiments can provide an estimate. In such experiments a number of fish are tagged after they were caught. Obviously, the situation is more complicated if most of the recoveries are made by the fishermen, since it is usually not possible to tag the fish caught without the fishermen being aware. If operational reasons are the main cause of tag loss, then we must be careful when the operational characteristics of the two interacting fisheries are very different, since it is likely that they will exhibit different reporting rates.
The processes behind Type-II tag losses are usually confounded as well. If we have a measure of fishing intensity (like fishing effort) that we can assume to be proportional to fishing mortality, we might possibly discriminate between removals due to the fishery and natural mortality and tag shedding. If we had double-tagging experiments then we might also be able to discriminate between natural mortality and a constant tag-shedding rate. This can be easily done, since tag shedding can be directly estimated from double tagging data. However, chances are that we will not have the necessary contrast in the data on fishing intensity to separate the effects of fishing and natural mortality. Moreover, any of these effects is likely to be confounded with the estimated exchange rates between fisheries.
Therefore, tagging experiments, in spite of being our best hope to quantify interactions, must be treated with caution and their sensitivities fully explored. In all cases, the possibility of better estimating the variability in levels of interactions can be improved upon by carrying out tagging experiments in multiple years. The question of reporting rates is likely to remain unresolved unless we can change drastically the way we recover the tags. An ideal (and, thus far, utopian) situation would be to design tags that could be detected at a distance by some passive device, like the pit tags used in salmon populations. If that proves unfeasible, perhaps some remedial (albeit expensive) measures can be implemented using port sampling programs, where the catch is inspected for undetected tags. If the conditions are standard and the fishery from which the catches originated can be established, a simple ratio between the tags returned by the fishery and the tags detected by the samplers can be used to determine relative reporting rates between fisheries.
Archival tags represent another potentially important source of data. Obviously, the possibility of obtaining information about the behaviour of the fish over a long period of time opens a large number of opportunities. Unfortunately, the high cost of the tags makes tagging large numbers of fish beyond most budgets. However, it might prove feasible for species with high exploitation rates for which we can expect numerous recoveries from a moderate number of tags released.
4.5 Identifying Interactions Using Studies on Stock Structure
Some of the research that can be done to assess the heterogeneity of the resource under exploitation can be carried out without direct information from the fishery. In any case, without knowledge of existing exploitation rates, we can only measure the potential for fishery interactions. Under this category, we encounter methods based on the biological characteristics of the resource. What we would like to measure here is the approximate degree of mixing of fish between different strata (areas, seasons, depths). If, for example, this mixing involves reproductive exchange, even at a minimal level, the population genetic structure will suggest that there is a single genetic population inhabiting both strata. If genetic markers indicate no reproductive exchange between strata, fishery interactions between those strata are unlikely. However, these indications may be deceptive (see below).
Studying the stock structure of the resource using morphological information (meristics and morphometrics) has a long tradition in fisheries. The underlying hypothesis in these studies is that morphological differences reflect either differences in genetics or differences in the environment during early life development. More recent variations on this approach have included studies on the morphology of the otolith. They represent a relatively inexpensive way of studying the problem of stock structure, but they do not allow direct assessment of the genetic structure of the population. The latter can be accomplished using various approaches:
1) Allozyme frequency. In this methodology, results from protein electrophoresis analyses are used to construct a contingency table of gene frequencies that can be used to test the null hypothesis of homogeneity in the frequencies at different sampling locations. The problem with this analysis is that the test has low power and large sample sizes must be used in order to detect small differences.The mtDNA analyses are better suited to detect differences than allozyme analysis given the increased resolution of the analysis. Recent techniques based on nuclear microsatellite loci, which apparently has a mutation rate of 10-3 /year, seem to offer an even better resolution.2) Mitochondrial DNA (mtDNA). Allozyme frequencies reflect the nuclear genome inherited through recombination whereas mtDNA-based studies offer the advantage that the mitochondria are inherited only from the female parent. There is no recombination of mtDNA and it has a higher mutation rate (10-5 /year) compared with nuclear genes.
The main problem with genetic studies is that to say that one has found a different “stock” genetically is quite different from what fisheries scientists typically view as a stock. Indeed a reproductive exchange of one individual between two areas per generation is all that is needed to result in those areas containing a single genetic population. Yet such a low mixing rate would cause fishery scientists to view them as separate stocks (NRC, 1994). Also, recent genetic studies of billfish suggest the existence of reproductively-isolated stocks that are mixed in the fishing grounds.
A more promising approach is based on the analysis of otolith microconstituents. The theory behind this method is that the differences in the environment throughout the life of the fish are reflected in the chemical composition of the otolith. As such, they offer a view of the environmental changes that the individuals in the population have been through, and may indicate movements between areas with different chemical characteristics. However, the resolution of these techniques depends on the magnitude of the differences in the environment. The technology for detection of a large range of minerals has progressed substantially in the last decade (Ianelli, 1993), but we still need a better understanding of the processes leading to differences in the chemical composition of otoliths.
An important use of genetic techniques might be to estimate the stock composition of the catch to monitor the dynamics of reproductively-isolated stocks that are mixed in the fishing grounds. This would involve sampling programs of a much larger scale than the studies discussed above. To date, no such program has been implemented. Such studies would be required if fisheries managers wish to ensure the conservation of each genetic population as well as each fishery stock.
4.6 Simulation as a Key Organisational Tool
Suppose that we have a collection (hopefully small) of possible mechanisms that could lead to interactions among identified components of a fishery. How can we organise these hypotheses in a way to better identify our data needs?
Perhaps one of the most useful tools that we have for that purpose today is simulation modelling. Uses of simulations are multiple, the one most commonly seen being the generation of artificial data to test the performance of some model or an estimation scheme (Sibert and Fournier, 1994, showed one such application). But more benefits can be derived from the use of simulations beyond testing the ability of a certain model to recover parameters. Simulations can be set up to assess the experimental design of tagging experiments under different hypotheses. The simulations can then be used to explore breadth and quantity of information that will be required to increase the power of the analysis and, especially, what will be required to reject certain hypotheses (see, for example, Bertignac, 1996). Simulations can provide the key element for the assessment of the power of different methods. Using a simulation, we can easily assess the likelihood of detecting or measuring a certain degree of interaction with a certain level of confidence. Forward simulations, or projections of the population also provide the flexibility of exploring different assumptions about recruitment.
In settings where the amount of data is reduced, simulations can be used to explore the alternative hypotheses that would give the same results and can be used to assess the costs and benefits of certain experiments or reducing uncertainty in certain key values. Therefore, simulations can provide guidelines for the future allocation of research resources. And simulations can easily be used to explore robustness of certain methods to violations of the assumptions.
Furthermore, a common experience in the use of simulations is that they improve our ability to understand and communicate the difficulties and constraints involved. Even if we do not have all the data required, a simulation exercise can help to establish what pieces of information are needed the most. The simulation analyses done by Kleiber and Baker (1987) or by Mullen et al. (1996) illustrate some of these points.
In summary, we need to expand the role that we assign to simulations. More than using them as tools to directly measure interactions, I foresee using simulations to identify the data collecting requirements that would enable us to reduce the range of possible hypotheses, and to identify the appropriate kinds of management actions.
5. STAGE TWO: OFFERING MANAGEMENT OPTIONS
Suppose that we have been fortunate and are confident of understanding the main processes governing some fishery interaction. That is, we have a credible model of how the population and the interacting fisheries are related. The next step will be to consider what are the available management options.
It is difficult to discuss management options in a general context, since the goals often differ in the various situations. In some scenarios, the management objective might be the maximisation of long-term total yield. In other scenarios, it might be more desirable to preserve sources of employment or protein for small coastal communities and the distribution of the yield would take precedence over the simple maximisation of yield. Therefore, the assessment of the possible strategies has to be done in terms of the specified management objectives.
In cases where the recruitment to the population is not strongly dependent on the spawning stock biomass, yield-per-recruit analysis can provide a valuable idea of the trade-offs between different levels of effort exerted by the interacting fisheries (Miyabe, 1994). The simplest situation occurs where we have the same age-specific selectivities or partial recruitment in both fisheries. If that is the case, the distinction between fisheries is unnecessary from the point of view of the yield of the population. Most likely, this will not be the case and the pattern of age-specific selectivities will differ as a consequence of the different gears employed or because of different choices of temporal and spatial strata combined with a distribution differential by age. In those cases, different relative levels of effort between the fisheries will result in a different mean age of the fish in the catch. Assuming that we cannot control the age-at-entry in the individual fisheries, an appropriate management objective might be to find the relative levels of effort between the interacting fisheries that would result in the best yield-per-recruit. An alternative objective might result from consideration of the economic value per unit weight of the fish caught by the two fisheries. This could differ when the technology available to the different fisheries is different, or the ability to preserve the fish, or the processing or the markets are different.
If the situation is more complex, for example, where the fishing pressure of the interacting fisheries is sequential rather than simultaneous, projections using simulation models over long periods can be used to assess costs and benefits of alternative management strategies.
The value of learning more about the characteristics of the population might also be incorporated. Because we will often be facing uncertainties in the modelling of the fishery interaction, we need to consider adaptive management plans that could lead to learning, in the sense of reducing the set of alternative hypotheses. Such strategies manipulate levels of fishing effort to provide greater contrast for measuring the response of the system. The benefits of such learning can be assessed and compare with the costs of obtaining the additional information. Unfortunately, adaptive management strategies are often unstable policies, and do not create the best conditions for the resolution of the conflicts implicit in any interactions problem.
Whatever the method we use to assess the possible management scenarios, we will need to provide managers with a consequence of the options in the form of decision tables (Medley, 1994).
6. CONCLUSIONS: SOME PARTING THOUGHTS
Whenever we are faced with a problem, the range of options we can explore is set by the tools and the raw material available. These two elements are not necessarily additive; we cannot compensate for the absence of data by increasingly sophisticated analytical techniques. This problem is relevant to us, since in many of the management problems involving interactions, data will be a scarce commodity. Fortunately, our problem promotes good science: the better we can identify and assess the level of an interaction, the better chances we have of finding a resolution of the conflict that would be acceptable to all parties. Simply concluding that we do not have all the necessary information to assess an interaction is not going to diffuse the conflict.
Therefore, as it has been said many times, our first priority should be to establish sampling programs according to our needs. In most cases, this will involve tagging experiments. In those rare cases where most of the information has been collected, there are analytical methods already developed that can be applied. But even if methods were not available, the time and effort required to develop them would be a minor expense compared with the time required to collect new information. The specific pieces of information that will help us to solve the puzzle can be identified only after a careful consideration of the alternative explanatory hypotheses. That is why emphasis was placed on the role of simulations as tools to help in the design of vast, expensive experiments such as tagging programs. Too often, we have begun the analysis of tagging data only to realise that problems in the original sampling design impede our ability to narrow down possible explanations.
7. REFERENCES CITED
Anganuzzi, A.A., R. Hilborn and J.R. Skalski. 1994. Estimation of size selectivity and movement rates from mark-recovery data. Can. J. Fish. Aquat. Sci. 51: 734-742.
Bertignac, M. 1996. A simulation model of tagging experiments of yellowfin in the western Indian Ocean. In: Shomura, R.S., J. Majkowski and R.F. Harman (eds.). Scientific Papers from the Second FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 23-31 January 1995, Shimizu, Japan. [This volume]
Boggs, C.H. 1994. Methods for analysing interactions of limited-range fisheries: Hawaii’s pelagic fisheries. In: Shomura, R.S., J. Majkowski and S. Langi (eds.). 1995. Interactions of Pacific Tuna Fisheries. Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 December 1991, Noumea, New Caledonia. FAO Fish. Tech. Pap. (336/1): 74-91
Deriso, R.B., R.G. Punsly and W.H. Bayliff. 1994. A Markov movement model of yellowfin tuna in the eastern Pacific Ocean and some analyses for international management. Fish. Res. 11: 375-395.
Hampton, J. 1994. A review of tuna-fishery interaction issues in the western and central Pacific Ocean. In: Shomura, R.S., J. Majkowski and S. Langi (eds.). Interactions of Pacific Tuna Fisheries. Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 December 1991, Noumea, New Caledonia. FAO Fish. Tech. Pap. (336/1): 138-157.
Hearn, W.S., and A. Mazanov. 1996. Interactions among fisheries: tag-recapture methods for estimating the effect of catches of changing intensity. In: Shomura, R.S., J. Majkowski and R.F. Harman (eds.). Scientific Papers from the Second FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 23-31 January 1995, Shimizu, Japan. [This volume]
Hilborn, R. 1990. Determination of fish movement patterns from tag recoveries using maximum likelihood estimators. Can. J. Fish. Aquat. Sci. 47: 635-643.
Ianelli, J. 1993. Studies on the population structure of skipjack tuna, Katsuwonus pelamis, in the central and eastern Pacific Ocean. Ph.D. dissertation, University of Washington, Seattle, Washington, USA. 215 p.
Ishii, T. 1979. Attempt to estimate migration of fish population with survival parameters from tagging experiment data by the simulation method. Invest. Pesq. 43: 301-317.
Kleiber, P. 1994. Types of tuna fishery interaction in the Pacific Ocean and methods of assessing interaction. In: Shomura, R.S., J. Majkowski and S. Langi (eds.). Interactions of Pacific Tuna Fisheries. Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 December 1991, Noumea, New Caledonia. FAO Fish. Tech. Pap. (336/1): 61-73.
Kleiber, P., and B. Baker. 1987. Assessment of interaction between North Pacific albacore, Thunnus alalunga, fisheries by use of a simulation model. U.S. Fish. Bull. 85(4): 703-711.
Kleiber, P., and A. Fonteneau. 1994. Assessment of skipjack fishery interaction in the eastern tropical Atlantic using tagging data. In: Shomura, R.S., J. Majkowski and S. Langi (eds.). Interactions of Pacific Tuna Fisheries. Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 December 1991, Noumea, New Caledonia. FAO Fish. Tech. Pap. (336/1): 94-107.
Lebreton, J.D., K.P. Burnham, J. Clobert and D.R. Anderson. 1992. Modeling survival and testing biological hypotheses using marked animals: a unified approach with case studies. Ecol. Monogr. 62: 67-118.
Majkowski, J., W.S. Hearn and R.L. Sandland. 1988. A tag-release/recovery method for predicting the effect of changing the catch of one component of a fishery upon the remaining components. Can. J. Fish. Aquat. Sci. 45: 675-84.
Medley, P.A.H. 1994. Estimating the impact of purse-seine catches on longline. In: Shomura, R.S., J. Majkowski and S. Langi (eds.). Interactions of Pacific Tuna Fisheries. Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 December 1991, Noumea, New Caledonia. FAO Fish. Tech. Pap. (336/1): 182-198.
Miyabe, N. 1994. A brief analysis of fishery interaction for bigeye tuna in the Pacific Ocean. In: Shomura, R.S., J. Majkowski and S. Langi (eds.). Interactions of Pacific Tuna Fisheries. Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 December 1991, Noumea, New Caledonia. FAO Fish. Tech. Pap. (336/1): 239- 248.
Mullen, A.J. 1996. A method to estimate movement from changes in estimated distributions, and then revise those estimates. In: Shomura, R.S., J. Majkowski and R.F. Harman (eds.). Scientific Papers from the Second FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 23-31 January 1995, Shimizu, Japan. [This volume]
Mullen, A.J., A.A. Anganuzzi, R.G. Punsly and G.J. Walker. 1996. Interactions between mode of fishing and category of vessel in catches of tunas in the eastern Pacific tuna fishery. In: Shomura, R.S., J. Majkowski and R.F. Harman (eds.). Scientific Papers from the Second FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 23-31 January 1995, Shimizu, Japan. [This volume]
NRC. 1994. An assessment of Atlantic bluefin tuna. Nat. Res. Coun., Nat. Acad. Sci., Washington, DC, USA. 148 p.
Porch, C.E., V.R. Restrepo, S.C. Turner and G.P. Scott. 1994. Virtual Population Analysis of Atlantic bluefin tuna incorporating movement and tagging data. ICCAT Document SCRS/94/73. 34 p.
Punt, A.E., and D.S. Butterworth. 1995. Use of tagging data with a VPA formalism to estimate migration rates of bluefin tuna across the North Atlantic. ICCAT Document SCRS/94/72. 36 p.
Salvadó, C.A.M. 1994. Discrete population field theory for tag analysis and fishery modeling. In: Shomura, R.S., J. Majkowski and S. Langi (eds.). Interactions of Pacific Tuna Fisheries. Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 December 1991, Noumea, New Caledonia. FAO Fish. Tech. Pap. (336/1): 122-136.
Sibert, J.R. 1984. A two-fishery tag attrition model for the analysis of mortality, recruitment and fishery interaction. Tuna and Billfish Assessment Programme, South Pacific Commission, Noumea, New Caledonia, Tech. Rep. 13.
Sibert, J.R., and D.A. Fournier. 1994. Evaluation of advection-diffusion equations for estimation of movement patterns from tag recapture data. In: Shomura, R.S., J. Majkowski and S. Langi (eds.). Interactions of Pacific Tuna Fisheries. Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 December 1991, Noumea, New Caledonia. FAO Fish. Tech. Pap. (336/1): 108-121.