William S. Hearn1
CSIRO2 Division of Fisheries, Marine
Laboratories
G.P.O Box 1538, Hobart, Tasmania, 7001, Australia
Alexander Mazanov3
School of Biological Science
University of New South Wales
PO Box 1, Kensington
New South Wales, 2033, Australia
1 Some of this work formed part of the principal author's doctorate awarded by University of New South Wales.2 Commonwealth Scientific and Industrial Research Organisation.
3 An earlier draft of this manuscript was prepared before Dr A. Mazanov's untimely death.
ABSTRACT
A tag-recapture experiment is suggested for determining the effect that a change in the fishing intensity of one fishery will have on its own catch and on the catch of another. The results are expressed as simple formulae in terms of one control variable: the proportional change in the fishing intensity of the altered fishery. There is no requirement to develop a complex parametric model of the dynamics of the population and fisheries or to collect comprehensive effort data. For the year-class being studied, the ideal experimental design requires that a representative sample of the fish caught by one fishery be tagged, and all tagged fish recaptured by the same fishery be re-released. In the second fishery (or fisheries), no fish need be tagged or re-released. Alternative equivalent procedures to re-releasing tagged fish are described. The dynamics of the fish population and fisheries are assumed to be independent of the size of the population, i.e., a linear dynamic system is postulated. The formulae are proven for two population models for which, (i) two fisheries catch fish from a common, homogeneously - mixed population, and (ii) two fisheries catch fish from separate grounds (fish may migrate between grounds). In some situations the formulae are size-based. Experimental design and formulae are developed to assess interactions when the fishing intensities of two or more fisheries are to be changed or a new fishery is proposed.
1. INTRODUCTION
Oceanic fish are mostly harvested as common resources. Many fish stocks are harvested by fisheries with different gear types, markets, seasons and fishing grounds. The degree to which the catch of one fishery decreases the catch of another at a later time is of concern to scientists, managers and fishers. With such knowledge, they may predict the effect that opening (or closing) a specific fishery may have on the catch of another fishery, which could assist managers prevent or resolve conflicts among fishers and optimise the exploitation of the resource.
The problem of fisheries interactions may be addressed in a number of ways (Kleiber, 1994). One approach is to develop parametric models of the dynamics of the fish population and associated fisheries. The parameter values are then estimated by fitting the model to detailed catch, effort and/or tag-recapture data (e.g., Sibert, 1984; Hilborn, 1990; Hampton, 1991; Kleiber and Fonteneau, 1994; Salvado, 1994; Sibert and Fournier, 1994; Hampton et al, 1995; Mullen, 1995; Sibert et al., 1995).
Another approach is to study statistical correlations, between different fisheries, of time-series of fisheries statistics (e.g., Fonteneau, 1986; Suzuki, 1988; Bayliff, 1994; Medley, 1994). However, the correlations observed do not necessarily indicate a causal relationship, given the relatively short length of most fisheries catch-and-effort time-series.
Results from data analyses can also be incorporated into computer simulation models that estimate fisheries interactions under a variety of reasonable assumptions (e.g., Kleiber and Baker, 1987; Bertignac, 1995; Kleiber and Fonteneau, 1995). The range of possible results and interpretations of such an approach are often too wide, although the results are frequently useful for identifying the most critical areas for further study.
An experimental tagging approach developed by Majkowski et al. (1988) simulates the proposed change in one fishery by tagging and releasing fish in that fishery and estimating the effect on the catch of another from the biomass of the second fisheries recaptures. The basic concept behind this method is that each fish tagged in one fishery represents a fish which another fishery is potentially deprived of. If all fish caught by the first fishery are tagged, or the proportion tagged are known, one can determine the biomass of fish that the second fishery loses of due to the existence of the first fishery. This approach, unlike other methods, does not require the development of a population model, estimates of many highly correlated parameters, complex analyses or detailed catch-and-effort data; however, its experimental requirements are demanding. Whilst our method differs from these in many aspects we nevertheless follow their basic approach.
Majkowski et al. (1988) used catch quota as the control variable which, for their method, implicitly requires that the age distribution of the change in catch of one fishery be the same as its present catch - an impractical condition for most fisheries, unless a total closure is contemplated. In other words it is assumed that changing the catch of that fishery does not affect the age distribution of its catches (the zero catch excepted). To avoid this problem, we use effort as the control variable. As a consequence our corresponding formulae are different from theirs. They also assumed the population to be steady-state before the change and for there to be a transition period (sometimes substantial) before the population reaches a new steady-state - a very difficult condition to meet. We consider a particular year-class, so our approach is essentially a yield-per-recruit analysis, although we show how the formulae apply to the steady-state case.
The formulae of Majkowski et al. (1988) express only the change in one fishery in terms of the change in the other (which is unknown) and the tagging information. We also develop corresponding formulae for this, as well as those that express the change in catch of each fishery in terms of the present catch of one fishery and the tagging information.
The mathematical development of the method in Majkowski et al. (1988) assumes a homogeneously-mixed population, although they applied it to an example in which the two fisheries are spatially distinct. Fish migration and spatial differences between fisheries are important characteristics of many fisheries interactions - the analytic and experimental techniques for estimating them are still a matter of active research. We model the homogeneous case, as well as a more complex population structure in which two fisheries operate on separate fishing grounds. In the latter case tagging in one ground only is needed (unlike parametric models which require tagging in both grounds, as well as detailed catch and effort statistics).
The experimental design described in the present paper requires that a representative sample of fish harvested in one fishery is tagged and released. (Note most analyses of tagging experiments assume a representative sample of the population is tagged.)
The approach requires that some fishers re-release tagged fish they recapture. Compliance with this requirement is unlikely, but analytic methods and experimental approaches are proposed as alternatives.
2. THEORY
2.1 General Requirements
Consider two separate fisheries, X and Y, catching fish from the same or different fishing grounds. Management may be considering reducing (or increasing) the fishing intensity of X by a proportion e and wish to assess the resultant change in Y's catch of a particular year-class. The fishing intensity of Y is assumed to remain unchanged. The more general objective is to estimate the effect on the catches of X and Y of changing the fishing intensities of both fisheries.
It is deemed that the following assumptions or conditions apply to the fishery, population and tagging experiment:
1. The rates of growth, natural and fishing mortalities, and migration are age-dependent and independent of population size.Conditions 1 and 2 are implicit in most yield-per-recruit and interaction analyses. If the population and fisheries were significantly influenced by environmental fluctuations, then tagging programs would need to be conducted over a number of years to average over the range of normal variation.2. Management can uniformly reduce the fishing intensity of fishery X by the desired proportion e, while keeping the fishing intensity of Y unchanged.
3. The normal conditions of tagging experiments apply: that tagging does not harm fish or change their growth or behaviour; that tags are durable, are not shed from fish and are all reported by finders (or the level of tag loss and non-reporting can be estimated); and that enough fish are tagged to allow statistically-reliable results.
4. The age-distribution of the present catch of X is almost certainly required (see discussion on next condition). In some cases the total weight, or number, of fish caught by fishery X is needed.
The requirements of Condition 3 are difficult to meet, particularly that concerning the reporting of tags. The assumptions in tagging experiments and procedures for meeting them, or coping with non-compliance, are examined by Beverton and Holt (1957), Paulik (1961), Beverton and Bedford (1963), Hearn et al. (1991) and Pollock et al., 1994; 1995), and the literature on tuna and billfish tagging is reviewed by Bayliff and Holland (1986).
2.2 Experimental Design
The experimental method presented here is based on an idea originally proposed by Alien (1953) for estimating the optimum size-limit for a fishery by equating the marginal yield to zero. Knight (1970) extended it to estimate the optimum size of a fishing fleet. More recently, Majkowski et al. (1988) further developed this approach to estimate the effects of interactions among fisheries.
We design a tagging experiment to estimate DKx and DKy, the corresponding potential changes in the biomasses of catches (or yields) from a specified year-class by fisheries X and Y due to the proposed change in the fishing intensity of X. Under the existing fishing regime, the total number of fish caught by fishery X from the specified year-class is Cx, having a biomass of Kx and a total biomass Ky of fish is caught by fishery Y. Apart from the need to comply with Condition 3, the experimental design requires two additional conditions:
5. Randomly tag N fish, having biomass W, of the selected year-class from the catch of fishery X. Tagging should be conducted over the entire period and geographical range that fish are susceptible to being caught by X, which may be for several years.Sometimes it may be difficult to determine which year-class a fish belongs to, particularly if many year-classes are harvested by fishery X. As illustrated in Appendix C, mathematical adjustments would need to be made if the age distribution of fish tagged was different from those caught by fishery X. Condition (5), in effect, requires that the age (or length) distribution of the catch of X be estimated by some means, i.e., implies that the first part of Condition (4) be met.
6. Fishers in fishery X are required to re-release (unharmed) a proportion e (the proposed proportional reduction in the fishing intensity of X) tagged fish they recapture (akin to the requirement of Majkowski et al. (1988) which requires that all fish recaptured by X be re-released) and report recapture weights (or lengths) to scientists. (This condition will be later modified.) Fishers in fishery Y are to retain all their recaptured fish and return tags with records of recapture weights (and/or lengths) to scientists.Condition 6 is an experimental analogue of the thinning technique that is used in computer simulation studies, which generates a required mortality rate from another more-easily-generated mortality rate (see Lewis and Shedler, 1979; Devroye, 1986, p264). Therefore, the expected fishing intensity of X on tagged fish is reduced by a proportion e from its level on untagged fish. Without Condition 6 only interactions, due to marginal changes of fishery X, can be estimated by this approach. The fishing intensity by Y on the tagged fish is assumed to remain unchanged.
If all vessels and their attributes are identical, then an equivalent requirement to Condition 6 is for a fraction e of vessels belonging to X to re-release all recaptures, while fishery X's other vessels retain all theirs. The assumptions allow the tagged fish to represent the entire fish population, both in number and biomass, for which the change in fishing regime is proposed. The biomasses of tagged fish caught and retained by X and Y are Rx and Ry, respectively.
Given these conditions, we will prove the following relationships first obtained in Hearn (1986) for a homogeneously-mixed population:
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
(2) |
|
and |
|
|
|
|
|
(3a) |
|
or |
|
|
|
|
|
(3b) |
In order to intuitively justify the validity of Equations (1) and (2), consider the effect of removing a proportion e of vessels from fishery X. Let these vessels be fishery X1 and the remainder of X be X2. This is equivalent to a proportional reduction e of fishing intensity if all vessels in fishery X are identical. We wish to assess the effects on the catches of X and Y of fishery X1 ceasing to catch and retain fish.
In a hypothetical experiment, suppose that all fish of a selected year-class caught by X1 are tagged and released, i.e., a number N = eCx of fish with biomass W = eKx are tagged. Also suppose that tagged fish recaptured by X1 are all re-released. Consequently fishery X1 does not retain any fish for sale and so the population of live fish, both tagged and untagged, become subject to fishing by fisheries X2 and Y. Thus all the tagged fish are those that fishery X1 would have caught and retained under the existing pattern of fishing, while the untagged fish would be the corresponding live population under the existing fishing regime. Hence, the tagged fish caught by Y represent the increase in the yield of Y, i.e., DKy = Ry. The increase in the yield of fishery X is equal to the biomass, Rx of the tagged fish caught by X2 less the biomass W = eKx foregone by X1. So Equations (1) and (2) are intuitively justified.
In an actual tagging experiment a representative sample of fish caught by X would be tagged, and eCx/N (or eKx/W) is the factor needed to scale up the experiment to the size of the commercial catch. These arguments also apply if fishery X is defined to be that part of the fishing gear which catches fish less than a certain size, with fishery Y defined as the remaining part of the gear, i.e that which catches fish at or above that size. Therefore, questions regarding size limits can also be addressed by the application of Equations (1-3).
If both fishing and population are assumed steady-state (i.e., recruitment, the pattern and intensity of fishing, catches, fish growth and behaviour are consistent from year to year) an alternative approach is to tag a representative sample of fish from the catch of X during one year over all year-classes. Here Kx and Ky represent stabilized annual yields of fisheries X and Y, rather than lifetime yields of a cohort. However, once the fishing intensity of X is changed there will be a transition period (up to the life-span of the species) before the age structure of the population stabilizes again. The change in yield, DKy, as derived from Equations (1) and (3 a), is an estimate of the change in the annual yield of Y between one stable population and the next. An advantage of this method, together with the steady-state assumption, is that, although it is based on an underlying aged-structured model, it does not require the age of any fish to be known, i.e., it is a size-based method.
If the effect of a marginal change to fishery X were to be estimated, then e would be close to zero, and so an approximate estimate of DKy, could be calculated from Equation (3a), with Rx and Ry being obtained from an experiment with no re-releasing. On the other hand, it may be planned to close fishery X altogether (i.e., e = 1). In this case Rx = 0 because fishery X would retain no tagged fish. Consequently, Equation (3a) becomes
|
|
(4) |
Equations (1) and (2) can be combined to give the total change DKT in the catch of both fisheries, viz.
|
|
(5) |
2.3 Population Model 1 - Homogeneously-Mixed Population
Consider two separate fisheries, X and Y, harvesting from a homogeneously-mixed population. The dynamics of the population of a particular year-class are assumed to be dependent only on age. The number of fish, P(t), at age t can be described by
|
|
(6) |
|
|
(7) |
2.4 Population Model 2: Two Fisheries Harvesting in Separate Grounds
For convenience let the separate grounds that fisheries X and Y operate in be called grounds X and Y, respectively. The dynamics of a particular year-class of fish can be described by
|
|
|
(8) |
|
and |
|
|
|
|
|
(9) |
Note that Equations (8) and (9) have been used previously to describe the dynamics of fishing acting on separate grounds, e.g., Beverton and Holt (1957) and Sibert (1984). The latter estimated natural and fishing mortality rates and transfer rates by analysing data from tagging in two fishing grounds and corresponding catch and effort information, but the rates of natural mortality and transfer were assumed constant. In the model represented by Equations (8) and (9), these rates are assumed to be dependent only on age, and for each ground the fish are assumed to be homogeneously mixed. Fish may be recruited to either or both fishing grounds, and r is the age that fish begin to be captured.
The solutions x(t) and y(t) of the differential Equations (8) and (9) have no general analytic expressions. However, if b(t) = 0 (i.e., fish migrate from X to Y, but not the reverse) analytic solutions can be obtained and the justification of Equations (1) and (2) follows a similar procedure to that given in Appendix A. If b(t) ¹ 0 a different approach is required, which is presented in Appendix B.
3. MODIFICATIONS
3.1 Increasing the Fishing Intensity of X
The experimental Condition 6 is designed for estimating the effect on catches of a specific reduction in the fishing intensity. However, modifying it to require all tagged fish that are recaptured by X be re-released is more appropriate to general analyses. Importantly, the formulae obtained, when this condition is implemented, are applicable to assessing the effects of increasing the fishing intensity of fishery X.
If management plans a proportional reduction of e (which would be negative if an increase were planned) in the fishing intensity of X, the estimates of Rx and Ry would be
|
|
|
(10) |
|
and |
|
|
|
|
|
(11) |
The biomass of tagged fish recaptured for the first time by X is Rx,0. In the experiment that assesses the effects of reducing the fishing intensity of X, the fraction, 1 - e, of these fish would be retained by fishery X which is equivalent to adding (1-e) Rx,0 to Rx as in Equation (10). Also a fraction e of fish caught by X would be re-released, which is equivalent to re-releasing all fish recaptured by X and giving each a value of e, which compounds each time the fish is re-released.
Clearly, Equations (10) and (11) have direct intuitive meanings only for 0 £ e £ 1. However, they do give correct estimates of Rx and Ry for negative values of e, i.e., when it is proposed to increase the fishing intensity of X by a factor e. To illustrate this, consider a proposal to double the fishing intensity of fishery X. Here e = -1 and the interpretation of Equation (10) follows. A tagged fish recaptured by X for the first time has double its caught weight added to Rx (i.e., 1 - e = 2), once for itself and once for an equivalent tagged fish that would have been caught if the fishing intensity of X had been doubled. However, this equivalent fish is still in the water so it is compensated for by re-releasing the tagged fish to the water with a value of minus one (i.e., e = -1). This explains why some terms in the expressions for Rx and Ry in Equations (10) and (11) become negative for negative values of e.
The implementation of the modified form of Condition 6 is preferred, as it allows a range of values of e (e £ 1) to be analysed, rather than one. Information is also obtained from more fish, which would tend to reduce the variance of the estimate of Rx and Ry. Additionally, it has the distinct advantage of simplifying re-release instructions to fishers.
A significant and representative proportion b of fishers may reliably re-release tagged fish without harm and record their weights (or lengths), e.g., if independent observers are on board. In such a case instruct other fishers not to re-release fish and modify Equations (10) and (11) by replacing ei with (e/b)i, but leave unaltered the (1-e) term in Equation (10).
The effect on the catch of fishery Y of starting a fishery in ground X, where none existed before, can also be assessed using this approach. Fish, with the same age composition as that intended for the catch of X, should be tagged during the period of its projected fishing season. Because no fish are presently being caught in ground X, then Rx = 0 and there can also be no re-releasing, so the effects of fishing in ground X cannot be correctly estimated from Equations (10) and (11). Nevertheless, if moderate yields from X are planned, a linear extrapolation of Equation (3a), with Rx = 0, would be approximately correct, i.e., Equation (4).
3.2 Changing the Fishing Intensity of Both Fisheries
Using simple interaction models, Beverton and Holt (1957) show that, for an over-harvested fish stock, a unilateral reduction of the fishing intensity of X always increases the catch of Y, but increases the catch of X only if its stock is over-harvested on a yield-per-recruit basis. To achieve an equitable share of the benefits of a reduction in fishing intensity, fisheries managers need to know the likely effects of changing the fishing intensity of both fisheries.
To achieve this objective, we suggest modifying Condition 5 by requiring that a random selection of fish caught by Y also be tagged. Like Condition 6, it is further required that a proportion g of all tagged fish recaptured by Y be re-released, including those tagged in ground X. Similarly a proportion g of all tagged fish recaptured by X should be re-released. The estimates of the changes in the catch of Y and X are:
|
|
|
(12) |
|
and |
|
|
|
|
|
(13) |
Note that Equations (12) and (13) can be extended to estimating interactions among many fisheries. To achieve this objective, a random selection of fish caught by each fishery, having biomass Wm (m = 1,2 ... n), is tagged. It is required that a proportion em of all tagged fish recaptured by fishery m be re-released, including those tagged in other grounds. The estimate of the change in the biomass, DKj, of the catch of fishery j is
|
|
(14) |
3.3 Substitutes for Fish that cannot be Re-released
In very few fisheries would fishers be expected to reliably re-release tagged fish without harm. Majkowski et al. (1988) proposed two methods for accounting for fish recaptured by fishery X that were not re-released. One has subsequently been found to be invalid4. However, their other proposal to tag and release equivalent fish for each one that is not re-released is a viable solution. This would require a low-level tagging program during the period when tagged fish are liable to be caught by X.
4 The method discounted recaptures by fishery X from the number (or biomass) of fish released. While this method allowed for natural mortality, the spatial structure of the population was not taken into account.If one can not implement a substitute tagging program, the experiment can be simply conducted without requiring re-releases and then equivalent tagged fish can be randomly chosen to serve as the substitutes. If one of the "pseudo" substitute fish is recaptured it would be counted twice, once as a fish recaptured for the first time and again as a substitute for another fish. A variation of this technique is illustrated in Appendix C for a special case.
Or it can be assumed that the population is stable and a random sample of the catch of X over all ages is tagged during one season. An approximation to re-releasing may be to let the substitute fish be one that was tagged at about the recapture size (but not necessarily at the same time) as the fish that was not re-released. This requires the assumption that temporal differences are not important.
For an homogeneously-mixed population it is readily shown from Equation (7) that for fish tagged at age t the proportion recaptured later by Y between ages t and t + dt (t £ t) is:
if there is no re-releasing. Comparing this equation with Equation (A8), which incorporates re-releasing, it can be seen that for every tagged fish recaptured by Y when there is no re-releasing there would be
recaptured if the required fish were re-released (note that a(t) = a(t) - eFx(t), see Equation (A4)). Given a value of the natural mortality, one could approximately estimate Fx(t) by cohort analysis of the tagging data (see Bayliff, 1971). Alternatively, if the effort data of fishery X and an estimate of the catchability coefficient are available, one can estimate Ry without re-releasing tagged fish. A similar procedure would be applied if an estimate of Rx was required, but it would need to be multiplied by 1 - e to allow for fish not retained by X. For fisheries in two grounds, these adjustments would be valid only while fish were in ground X (i.e., for some unknown period smaller than t-T); therefore the values of Ry and Rx obtained in this way would be overestimated.
3.4 Estimating Standard Errors
If DKy is estimated from the first form of Equation (1) then, using the delta method (see Seber, 1973, equation 1.11 p9) with Cx and Ry independent and assuming the term involving Var(Cx)Var(Ry) is negligible,
|
|
(15) |
However, if DKy is estimated from the second part of Equation (1), then similarly
|
|
(16) |
Adjustments would need to be made to the variance formulae in Majkowski et al. (1988) for them to be suitable for Equations (2), (3a), (5), (12), and (13). The procedures used to adjust results when assumptions are not complied with may be too complex for an analytic expression of variance. In such a case either of the jackknife or bootstrap methods could be used, as all the expressions are algebraic.
If fish form large schools, a tagging vessel would tag fish from some of the schools that would be subject to fishing by X. As the integrity of schools may persist for some time, the assumption of independence between fish may not hold. In such a case a bootstrap approach with schools as the basic unit may be preferable.
4. DISCUSSIONS AND CONCLUSIONS
We have demonstrated that Equations (1) and (2) generally hold for both increasing and decreasing effort. Therefore, tagging the catch from one ground (X) is sufficient if assessment of the effects of changing the fishing intensity of X is the only knowledge required. (Methods that derive, with good precision, a full solution of the dynamics of the population require that fish also be tagged in Y, e.g Bertignac, 1995.) Additionally, our formulae require estimates of the number (Cx) or biomass (Kx) of fish caught by fishery X and its age composition, but do not need detailed effort statistics. Tagging in ground X and not in Y would make more resources available to tag substitute fish or put independent observers aboard vessels in ground X to re-release fish. However, if a number of management options were being considered the experimental design would need to allow for all cases, which could be more expensive (e.g., tagging in both grounds).
The estimate of
 in Equation (3b) requires
only tagging data and the age distribution of the catch, (i.e., it does not need
estimates of Cx or Kx), and is less
sensitive to e than the Equation (1)
estimate, which could be important if e is
not proportional to the measured change in effort (i.e., Condition 2 not met).
Moreover, it does not require management to be committed to forecasting the
absolute value of the change in catch of Y, which may be critical if
recruitment is variable. It also addresses the question of what is the catch
weight gained by fishery Y per unit of weight foregone by fishery
X, which is particularly relevant when there is no existing fishery in
ground X (in which case Equations (1) and (2) cannot be
applied).
in Equation (3b) requires
only tagging data and the age distribution of the catch, (i.e., it does not need
estimates of Cx or Kx), and is less
sensitive to e than the Equation (1)
estimate, which could be important if e is
not proportional to the measured change in effort (i.e., Condition 2 not met).
Moreover, it does not require management to be committed to forecasting the
absolute value of the change in catch of Y, which may be critical if
recruitment is variable. It also addresses the question of what is the catch
weight gained by fishery Y per unit of weight foregone by fishery
X, which is particularly relevant when there is no existing fishery in
ground X (in which case Equations (1) and (2) cannot be
applied).
If the fish caught by X are young the length-frequency
modes may be distinct, thus allowing reliable year-class identification. If so
Equation (3b) essentially becomes a size-based formula. Also tagging in ground
X is likely to be completed in only two or three years, thus increasing
the feasibility of this approach. Moreover, if the average size offish caught by
Y is much larger than those caught by X there exists a potential
for a strong fishery interaction, i.e
 may be substantial, which
will be of concern to fishers operating in fishery Y and to managers.
Additionally, the natural mortality and migration rates of young fish may vary
markedly as they grow older: our approach deals with this aspect. We thus have a
situation where a fishery interaction may be substantial, for which this method
is likely to be particularly appropriate.
may be substantial, which
will be of concern to fishers operating in fishery Y and to managers.
Additionally, the natural mortality and migration rates of young fish may vary
markedly as they grow older: our approach deals with this aspect. We thus have a
situation where a fishery interaction may be substantial, for which this method
is likely to be particularly appropriate.
Experimental design and formulae, which are analogues of Equations (1) and (2), were developed for assessing interactions where the fishing intensity of two (or more) fisheries may be changed. This requires tagging in two grounds and catch information from each. The results generated from this procedure are expressed in terms of two (or more) control variables, which allows managers to allocate a more equitable share between fisheries of the benefit or loss that flows from the changes. Unfortunately, there is no analogue of Equations (3a) for this experimental design.
One difficulty with our approach is that a change in effort is not likely to be uniform over time and space (Condition 2). For example, an area may not be fished at all or the fishing -season may be shortened. If one could predict how the reduction in effort was going to be distributed, then the fishery could be considered as a number of sub-fisheries. The experiment would be designed accordingly and Equation (14) used for analyses.
In Equation (11) Ry,0 would be the dominant
term in Ry unless the catch of X is very high. This
dominant term is not affected by non-re-releasing and/or non-reporting by
fishery X. If a reduction in the fishing intensity of X is
proposed, then Ry,0 is a lower bound for
Ry, and hence a lower bound for DKy can be estimated from Equation (1).
Similarly, Rx,0 is a lower bound for
Rx and so a lower bound for the ratio
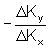 can be obtained from
Equation (3b).
can be obtained from
Equation (3b).
The use of Equations (8) and (9) with general age-dependent coefficients allows Equations (1) and-(2) to be established for a simple spatial population model, a considerable advance over Majkowski et al. (1988), who established their formulae only for homogeneous populations. One may wish to construct more elaborate population models that incorporate spatially-varying advection and diffusion as, for example, those of Sibert and Fournier (1994). In such a case the proof of Equations (1) and (2) could be established in a similar way to that in Appendix B, by examining the differential properties of an analogue of Equations (B 11) and (B 12).
An important element of this experimental design - re-releasing a certain proportion of fish - is difficult to implement, but alternative strategies are to, re-release all fish, tag substitute fish, make mathematical adjustments, or use effort data in some cases. The value of placing independent observers on fishing vessels is not only to ensure the re-release of tagged fish but also to allow assessments of the catch and/or tag non-reporting, which are difficult problems to address by other means.
Equations (1-3) essentially represents a Petersen approach (see Ricker, 1975, p77). The essential concept is intuitively simple, even if difficult to establish for a complex population model. Even so, a number of assumptions need to be met, particularly those relating to the tagging experiment. Other tagging approaches must also meet the normal tagging assumptions (Condition 3), but tagging a representative sample of the catch of X (Condition 5) and re-releasing recaptured fish (Conditions 6) are requirements specific to this method. An advantage of the approach is that it avoids the need to derive the age-varying coefficients implicit in Equations (6), (8) and (9).
The sum of DKy and DKx (= DKT) from Equations (12) and (13) gives the total change in yield in terms of the change of fishing intensities e and g in fisheries X and Y. This allows curves of equal value of DKT to be plotted against e and g for the information of managers. The application of Equation (14) would extend this approach to evaluate the effects of changing the fishing intensities of several fisheries.
The estimates of fisheries interaction obtained from such experiments could make a valuable contribution to helping managers evaluate proposed changes in the fishing intensity of different fishery components.
5. ACKNOWLEDGMENTS
We thank Drs K. Allen, W. Bayliff, C. Fandry, V. Lyne, V. Mawson, T. Polacheck and Mr G. Leigh for helpful comments on an earlier draft of the paper. We are also grateful for Dr J. Majkowski's suggestion that some recaptured fish be re-released, and Dr D. Jackett for advice about linear differential equations.
6. REFERENCES CITED
Allen, K.R. 1953. A method for computing the optimum size-limit for a fishery. Nature (Lond.) 172: 210.
Bayliff, W.H. 1971. Estimates of the rates of mortality of yellowfin tuna in the eastern Pacific Ocean derived from tagging experiments. Bull. I-ATTC 15: 379-436.
Bayliff, W.H. 1994. Interactions among fisheries for northern bluefin tuna, Thunnus thynnus, in the Pacific Ocean. In: R.S. Shomura, J. Majkowski and S. Langi (eds.). Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 Dec. 1991, Noumea, New Caledonia, pp 249-263. FAO Fish. Tech. Pap. 336 Vol 1, 326 pp.
Bayliff, W.H. and K.N. Holland. 1986. Materials and methods for tagging tuna and billfishes, recovering the tags, and handling the recapture data. FAO Fish. Tech. Pap. 279, 36 pp.
Bertignac, M. 1996. A simulation model of tagging experiments of yellowfin in the western Indian Ocean. In: Shomura, R.S., J. Majkowski and R.F. Harman (eds.). Scientific Papers from the Second FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 23-31 January 1995, Shimizu, Japan. [This volume]
Beverton, R.J.H. and B.C. Bedford. 1963. On the effect of "holding" tagged fish for various periods before release. ICNAF Spec. Pub. 4: 348-358.
Beverton, R.J.H. and S.J. Holt. 1957. On the dynamics of exploited fish populations. Fishery Invest., London, Ser. 2, Vol. 19, 533 pp.
Devroye, L. 1986. Non-uniform random variate generation. Springer-Verlag, New York, 834 pp.
Fonteneau, A. 1987. Surface versus longline tropical fisheries in the Atlantic Ocean: what interactions? Expert Consultation on Stock Assessment of Tunas in the Indian Ocean, 4-8 December 1986, Colombo, Sri Lanka. Collect. Vol. Indo-Pac. Tuna Dev. Mgt. Programme: 191-216.
Hampton, J. 1991. Estimation of southern bluefin tuna Thunnus maccoyii natural mortality and movement rates from tagging experiments. Fish. Bull., U.S. 89: 591-610.
Hampton, J., T. Lawson, P. Williams and J. Sibert. 1996. Case study of fishery interaction in a Pacific island country: Kiribati. In: Shomura, R.S., J. Majkowski and R.F. Harman (eds.). Scientific Papers from the Second FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 23-31 January 1995, Shimizu, Japan. [This volume]
Hearn, W.S. 1986. Mathematical methods for evaluating marine fisheries. PhD thesis, University of New South Wales, Australia. 195 p.
Hearn, W.S., G.M. Leigh and R.J.H. Beverton. 1991. An examination of a tag-shedding assumption, with application to southern bluefin tuna. ICES J. Mar. Sci. 48: 41-51.
Hilborn, R. 1990. Determination of fish movement patterns from tag recoveries using maximum likelihood estimators. Can. J. Fish. Aquat. Sci. 47: 635-643.
Kleiber, P. 1994. Types of tuna fishery interaction in the Pacific Ocean and methods of assessing interaction. In: R.S. Shomura, J. Majkowski and S. Langi (eds.). Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 Dec. 1991, Noumea, New Caledonia, pp 61-73. FAO Fish. Tech. Pap. 336 Vol 1, 326 pp.
Kleiber, P. and B. Baker. 1987. Assessment of interaction between North Pacific albacore, Thunnus alalunga, fisheries by use of a simulation model. Fish. Bull. 85: 703-711.
Kleiber, P. and A. Fonteneau. 1994. Assessment of skipjack fishery interaction in the eastern tropical Atlantic using tagging data. In: R.S. Shomura, J. Majkowski and S. Langi (eds.). Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 Dec. 1991, Noumea, New Caledonia, pp 94-107. FAO Fish. Tech. Pap. 336 Vol 1, 326 pp.
Kleiber, P. and A. Fonteneau. 1996. Atlantic yellowfin interactions. In: Shomura, R.S., J. Majkowski and R.F. Harman (eds.). Scientific Papers from the Second FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 23-31 January 1995, Shimizu, Japan. [This volume]
Knight, W. 1970. A possible optimization experiment in fishery management. J. Fish. Res. Board Can. 27: 961-963.
Lewis, P.A.W. and G.S. Shedler. 1979. Simulation of nonhomogeneous Poisson processes by thinning. Naval Research Logistics Quarterly 26: 403-413.
Majkowski, J., W.S. Hearn and R.L. Sandland. 1984. An experimental determination of the effect of increasing the minimum age (or size) of fish at capture upon the yield per recruit. Can.]. Fish. Aquat. Sci. 41: 736-743.
Majkowski, J., W.S. Hearn and R.L. Sandland. 1988. A tag-release/recovery method for predicting the effect of changing the catch of one component of a fishery upon the remaining components. Can. J. Fish. Aquat. Sci. 45: 675-684.
Medley, P. 1994. Estimating the impact of purse-seine catches on longline. In: R.S. Shomura, J. Majkowski and S. Langi (eds.). Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 Dec. 1991, Noumea, New Caledonia, pp 182-198. FAO Fish. Tech. Pap. 336 Vol 1, 326 pp.
Mullen, A. 1996. A method to estimate movement from changes in estimated distributions, and then revise those estimates. In: Shomura, R.S., J. Majkowski and R.F. Harman (eds.). Scientific Papers from the Second FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 23-31 January 1995, Shimizu, Japan. [This volume]
Paulik, G.J. 1961. Detection of incomplete reporting of tags. J. Fish. Res. Board Can. 18: 817-832.
Pollock, K.H., K. Tsai and J.M. Hoenig. 1994. Band return models: use of solicited bands and separation of hunting and natural mortality. J. Wildl. Manage. 58: 193-198.
Pollock, K.H., M.J. Conroy and W.S. Hearn. 1995. Separation of hunting and natural mortality using ring-return models: an overview. J. Appl. Stat. 22: 557-566.
Ricker, W.E. 1975. Computation and interpretation of biological statistics of fish populations. J. Fish. Res. Board Can., Bull. 191, 382 pp.
Salvado, C. 1994. Discrete population field theory for tag analysis and fishery modeling. In: R.S. Shomura, J. Majkowski and S. Langi (eds.). Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 Dec. 1991, Noumea, New Caledonia, pp 122-136. FAO Fish. Tech. Pap. 336 Vol 1, 326 pp.
Seber, G.A.F. 1973. The estimation of animal abundance and related parameters. Griffin, London, 506 pp.
Sibert, J.R. 1984. A two-fishery tag attrition model for the analysis of mortality, recruitment and fishery interaction. South Pacific Commission, Tuna and Billfish Assessment Programme, Tech. Rep. 13, Noumea, New Caledonia. 27 p.
Sibert, J. and D. Fournier. 1994. Evaluation of advection-diffusion equations for estimation of movement patterns from tag recapture data. In: R.S. Shomura, J. Majkowski and S. Langi (eds.).Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 Dec. 1991, Noumea, New Caledonia, pp 108-121. FAO Fish. Tech. Pap. 336 Vol 1, 326 pp.
Sibert, J., J. Hampton and D. Fournier. 1996. Skipjack movement and fisheries interaction in the Western Pacific. In: Shomura, R.S., J. Majkowski and R.F. Harman (eds.). Scientific Papers from the Second FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 23-31 January 1995, Shimizu, Japan. [This volume]
Suzuki, Z. 1988. Study of interaction between longline and purse seine fisheries on yellowfin tuna, Thunnus albacaris (Bonnaterre). Far Seas Fish. Res. Lab., Bull. 25: 73-144.
APPENDIX A HOMOGENEOUSLY MIXED POPULATION: PROOF OF EQUATIONS (1) AND (2)
The rate that fishery X catches fish is Fx(t)P(t), so from Equation (7) the number (Cx) and biomass (Kx) of fish caught by X from the selected year-class are, respectively,
|
|
|
(A1) |
|
and |
|
|
|
|
|
(A2) |
|
|
(A3) |
|
|
(A4) |
If the changed regime, with its associated fish population represented by Equation (A4), operated for the entire lifetime of the selected year-class, the biomasses, K*x and K*y, of fish caught by fisheries X and Y would be
|
|
|
|
and |
|
|
|
|
|
|
|
(A5) |
|
and |
|
|
|
|
|
(A6) |
|
|
(A7) |
Derivation of Equation (1)
By replacing t for r in Equation (A4) it can be seen that, of fish tagged from the catch of X at age t, the proportion recaptured later by Y between ages t and t + dt (t £ t) is expected to be
|
|
(A8) |
|
|
(A9) |
|
|
(A10) |
|
|
(A11) |
Derivation of Equation (2)
Of fish tagged from X at age t the proportion recaptured later by X between ages t and t + dt (t £ t) and retained is expected to be
|
|
(A12) |
|
|
(A13) |
|
|
(A14) |
|
|
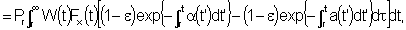
which from Equations (A2) and (A5)
= DKx + DKy thus establishing Equation
(2).
APPENDIX B TWO FISHING GROUNDS: PROOF OF EQUATIONS (1) AND (2)
At age t the rate that X catches fish is Fx(t)x(t)) and hence the total number, Cx and biomass, Kx of fish caught by X from the selected year-class are
|
|
|
(B1) |
|
and |
|
|
|
|
|
(B2) |
|
|
(B3) |
|
|
|
(B4) |
|
and |
|
|
|
|
|
(B5) |
Under the proposed new fishing regime, the corresponding biomasses caught by fisheries X and Yon their respective grounds are, similarly to Equations (B2) and (B3), expected to be
|
|
|
(B6) |
|
and |
|
|
|
|
|
(B7) |
|
|
|
(B8) |
|
and |
|
|
|
|
|
(B9) |
|
|
(B10) |
Simplification of Proofs
If one fish is tagged in X at age t and subject to the proposed fishing regime, then
the probability of its being in X at age t is defined as
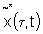 and in Y as
and in Y as
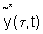 (i.e.,
Green's functions). We aim to show that it is sufficient to prove
(i.e.,
Green's functions). We aim to show that it is sufficient to prove
|
|
|
(B11) |
|
and |
|
|
|
|
|
(B12) |
Of fish tagged in X at age t, the proportion recaptured later by Y between ages t and t + dt (t £ t) is expected to be
|
|
(B13) |
|
|
(B14) |
|
|
(B15) |
Of the fish tagged in ground X at age t, the proportion expected to be caught and retained by fishery X between ages t and t+dt (t t) is
|
|
(B16) |
|
|
(B17) |
|
|
(B18) |
|
|
i.e., Equation (B 12), to justify Equation (2).
Proof of Equations (B11) and (B12)
Let the LHSs of Equations (B11) and (B 12) be
|
|
F(t) =
x*(t)-x(t) |
|
and |
|
|
|
Y(t) =
y*(t)-y(t) |
|
|
|
|
and |
|
|
|
|
|
|
|
(B19) |
|
and |
|
|
|
|
|
(B20) |
Furthermore,
|
|
(B21) |
|
|
|
|
|
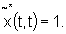 Additionally,
Additionally,
|
|
(B22) |
|
|
|
|
|
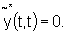 Additionally,
Additionally,The linear differential Equations (B19) and (B20) for F(t) and Y(t) are identical to Equations (B21) and (B22) for F(t) and Y(t) and the initial conditions are also equal. Therefore F(t) = F(t) and Y(t) = Y(t), thus proving Equations (B 11) and (B 12) and so justifying Equations (1) and (2).
APPENDIX C ASSESSING THE EFFECT OF ONE PULSE FISHERY UPON ANOTHER: AN EXACT SOLUTION WHEN NO FISH ARE RE-RELEASED
Consider two separate fishing grounds X and Y. Assume fishing takes place during a short period at the same time each year for both fisheries. For fish of a particular cohort, let Px1 fish of age 1 year and Px2 fish of age 2 years be recruited to ground X just before the corresponding fishing season. The numbers, Py2 and Py3, of fish recruited to ground Y are similarly defined.
Proportions fx1 and fx2 of fish aged 1 and 2 years respectively, are caught by fishers in ground X and proportions fy2 and fy3 of fish aged 2 and 3 years are caught by fishers in ground Y. The survival parameter Sxx1 is the fraction of fish initially in X and remaining in X which survives from the beginning of season 1 to the beginning of season 2, i.e it includes the effect of fishing, migration and natural mortality. Parameter Sxy1 is the proportion of fish of age 1 in X that moves to Y and survives to age 2. Parameters Sxy2 and Syy2 are similarly defined. It is assumed that natural mortality and migration can be ignored during the short fishing season.
The numbers of fish in the commercial catches are Cx1, Cx2, Cy2 and Cy2. Symbols in bold represent numbers of fish that need to be observed, or estimated by some means, which are the input information into the interaction estimation procedure.
The purpose of this analysis is illustrate how to estimate the effect on the catch numbers of Y of closing down fishery X when no tagged fish are re-released. It is assumed that the mortality parameters are independent of population size and that 1 and 2 year old fish in X can be identified with sufficient accuracy. We construct a table of the numbers of fish caught under the existing fishing regime.
Table C1. The commercial catch numbers of the present fishing regime, by age and fishing ground, in terms of recruitment, survival and fishing intensity.
|
Ground caught |
Catch numbers at age |
||
|
1 |
2 |
3 |
|
|
X |
Cx1 |
Cx2 |
|
|
Px1fx1 |
{Px1Sxx1+Px2}fx2 |
|
|
|
Y |
|
Cy2 |
Cy3 |
|
|
{Px1Sxy1+Py2}fy2 |
{Px1Sxx1+Px2} Sxy2fy3
+ {Px1Sxy1+Py2}Syy2fy3+Py3fy3 |
|
|
|
Sxx1 =
S'xx1(1-fx1) |
or |
S'xx1-Sxx1 =
Sxx1fx1/(1-fx1), |
(C1) |
|
|
Sxy1 =
S'xy1(1-fx1) |
or |
S'xy1-Sxy1 =
Sxy1fx1/(1-fx1), |
(C2) |
|
and |
Sxy2 =
S'xy2(1-fx2) |
or |
S'xy2-Sxy2 =
Sxy2fx2/(1-fx2). |
(C3) |
Table C2. After closing down fishery X: the commercial catch numbers by age, in terms of assumed recruitment, survival and fishing intensity.
|
Ground caught |
Numbers in the catch at age |
||
|
1 |
2 |
3 |
|
|
X |
C'x1 |
C'x2 |
|
|
0 |
0 |
|
|
|
Y |
|
C'y2 |
C'y3 |
|
|
{Px1S'xy1 + Py2}fy2 |
{Px1S'xx1 + Px2}S'xy2fy3
+ {Px1S'xy1 + Py2}Syy2fy3
+ Py3fy3 |
|
|
|
|
|
|
(C4) |
Tagging experiment
Just before the fishing season begins tag Nx1 one year olds in X and a year later tag Nx2 two year olds in the same ground. The number recaptured from ground X at age j from fish tagged at age i is rxij. A similar definition applies to ryij. It is assumed that the age of a fish is known at release with sufficient accuracy, if fish are young this could be determined from length-frequency modes. The numbers of recaptures expressed in terms of population parameters are:
Table C3. The numbers of recaptures of tagged fish of the present fishing regime, by age of release and by age and fishing ground of recapture, in terms of numbers tagged, survival and fishing intensity.
|
Number tagged |
Ground recaptured |
Numbers of recaptures at age |
||
|
1 |
2 |
3 |
||
|
Nx1
|
X |
rx11 |
rx12 |
|
|
Nx1fx1 |
Nx1Sxx1fx2 |
|
||
|
Y |
|
ry12 |
ry13 |
|
|
|
Nx1Sxy1fy2 |
Nx1Sxx1Sxy2fy3
+ Nx1Sxy1Syy2fy3 |
||
|
Nx2
|
X |
|
rx22 |
|
|
|
Nx2fx2 |
|
||
|
Y |
|
|
ry23 |
|
|
|
|
Nx2Sxy2fy3 |
||
|
|
(C5) |
We now deal with non-compliance with the re-releasing requirement. Firstly, at the end of season i some Nxi-rxii fish remain of the Nxi initially tagged at the beginning of the season. If all fish had been re-released then Nxi would have remained. To allow for this discrepancy, subsequent recaptures of these fish should be multiplied by the factor Nxi(Nxi-rxii) or 1/(1- fxi). Accordingly (ry12 + ry13)Nx1/(Nx1-rx11) + ry23Nx1Nx2Cx2/[Cx1Nx2(Nx2-rx22)] will contribute to Ry.
Next, from the Nx1 fish tagged in year 1 some rx12 Nx1/(Nx1-rx11) should have been caught in X at age 2 and re-released, but were not. These need to be represented by the Nx2-rx22 tagged fish that remain after season 2 from the Nx2 tagged just before it began. So the additional contribution to Ry is rx12rx23Nx1/[(Nx1-rx11)(Nx2-rx22)].
Consequently, from Equation (C5) the estimate of the change in the catch of Y in terms of observed fish numbers is
|
DCy =
Cx1 [ry12 +
ry13 +
rx12ry23/(Nx2 -
rx22)]/(Nx1 -
rx11) +
Cx2ry23/(Nx2 -
rx22). |
C6 |
which simplifies to the RHS of Equation (C4) as required. Thus we have illustrated how to make mathematical adjustments when the ideal experiment is not implemented. In fisheries with more complex dynamics the mathematical adjustments may need to be expressed as an iterative process to allow computer analyses.
It is noted one cannot solve for all model parameters because there are 6 equations represented in Equation (C1) and Table (C3) with 8 unknowns: fx1, fx2, fy2, fy3, Sxx1, Sxy1, Sxy2, and Syy2. Other information contributes equal numbers of equations and unknowns.
Equations can be adjusted to estimate the change in the weight of fish caught by fishery Y. Additionally, this analysis could also be extended to allow fx1, and fx2 to be control variables, e.g. fx1 = 0 is the conventional size limit case. It could also be extended to cases where more age classes are harvested in X and/or Y or where fish are tagged in both grounds.