Xi He
Joint Institute of Marine and Atmospheric Research
School of Ocean and Earth Science and Technology
University of Hawaii
Honolulu, Hawaii 96822 USA
Christofer H. Boggs
Honolulu Laboratory
Southwest Fisheries Science Center
National Marine Fisheries Service, NOAA
Honolulu, Hawaii 96822 USA
ABSTRACT
Bigeye tuna (Thunnus obesus) and yellowfin tuna (T. albacares) are important in several fisheries that operate within the Hawaii exclusive economic zone (EEZ). These species are believed to be widely distributed across the Pacific Ocean, and the strong seasonality of catch rates suggests extensive exchange of fish between the Hawaii EEZ and other regions. Nevertheless, Hawaii fishermen and fishery managers have concerns that local catches could reach levels high enough to depress local fish abundance.
Time series analysis was used to test the null hypothesis that local catches had no effects on local abundance in the Hawaii EEZ from 1962 to 1992. Transfer function models were used in the analysis with local catches as the input variables and catch per unit effort (CPUE) indices from the Hawaii domestic handline, longline, and troll fisheries as the output variables. Time series of both catch and CPUE were differenced to remove long-term trends and seasonality before the analysis. The predominant significant findings were positive relationships between catch and CPUE at the monthly time scale and zero lag, for both species and all fisheries. Catches increased when CPUE was increased, and decreased when CPUE decreased. Few negative relationships were found at any lags. The analysis showed no significant negative effects of catches on CPUE for bigeye tuna at an annual time scale. A barely significant negative effect on longline CPUE was found at the monthly time scale at a lag of two months. For yellowfin tuna, a barely significant negative effect on longline CPUE was found at the annual time scale at a lag of one year. Model forecasts were made for 1993 and 1994 and compared with preliminary 1993 data.
1. INTRODUCTION
Bigeye tuna (Thunnus obesus) and yellowfin tuna (Thunnus albacares) are targeted by several of Hawaii's commercial fisheries, and yellowfin tuna are also targeted by the recreational fishery. Catches of these two species have composed an important fraction of Hawaii's total fish catch since the development of the Hawaii longline fishery in the 1920s and the expansion of the small-vessel troll and handline fisheries in the 1970s (Boggs and Ito, 1993). However, studies on the effects of local catches on local abundance of both species have been few for two reasons. First, only small fractions of what are thought to be widely distributed stocks are seasonally available to Hawaii fisheries, so local catches should have little effect on overall population abundance (Suzuki, 1993; Miyabe 1993; Skillman et al., 1993). Second, tunas were not included as pelagic management unit species until the Magnuson Act was amended in 1991 and the pelagic fishery management plan was amended by the Western Pacific Regional Fishery Management Council (WPRFMC) in 1992 (Federal Register, vol. 57, p. 48564). Recently, rapid expansion of the Hawaii longline fishery has caused concern about whether local depletion of both species can occur at short temporal scales (Boggs and Ito, 1993; Boggs, 1994). Gear conflicts between longliners and fishermen using troll and handline gears were also a problem. These concerns prompted the federal fisheries management authority (the WPRFMC) to develop several regulations for Hawaii fisheries that include limits on the numbers and size of longline vessels and closure of coastal areas to longline fishing (Pooley, 1993).
We evaluated effects of total catches of bigeye tuna and yellowfin tuna on local abundance within the Exclusive Economic Zone (EEZ) of the main Hawaiian Islands by applying time series models to long-term fisheries catch data. Catch per unit effort (CPUE) was used as an index of apparent local abundance. We hypothesized that local catches had no effects on local abundance of yellowfin tuna and bigeye tuna. We tested the hypothesis with time series models that used combined local catches by domestic and foreign fisheries as input variables and domestic CPUE values as output variables. For each model, if the parameters relating catch to CPUE were not significantly negative, we did not reject the null hypothesis that catches had no effects on CPUE and inferred that local fisheries may not affect local abundance of fish. We used time series data at two temporal scales (monthly and annual) to test the hypothesis.
2. METHODS AND MATERIALS
2.1 Time Series Models
We used transfer function models in this analysis (Wei, 1990; Bowerman and O'Connell, 1993; Carpenter, 1993). Transfer functions can be viewed as relationships between anomalies of input and output variables. The anomalies are the remaining time series after serial dependencies and seasonal trends in the original series are removed by ARIMA models (Autoregressive Integrated Moving Average models, Wei, 1990). If anomalies in the output variable are not explainable by their own series dependency or seasonality but follow anomalies in the input variable, then there exist relationships between the input and output variables, and a transfer function can be fit.
The general form of the simplified linear transfer function can be represented as
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
Xt=Xt-Xt-d |
(5) |
|
|
(6) |
Data from 1962-1992 were used to build the transfer function models (see next section for details), resulting in 31 data points at the annual and 372 at the monthly time scale. Construction of all transfer function models and estimates of all parameters were done using the SAS statistics program, version 6.09 (SAS Institute, Inc., 1993). Detailed procedures on construction of models and estimation of parameters can be found in Wei (1990), Bowerman and O'Connell (1993), and SAS Institute, Inc. (1993). In some situations several models with different parameter values provided significant fits to the same data. These models were presented and compared based on the goodness-of-fit of the models. If no lag terms were significant, the model with b=0 and s=0 was presented.
After the models were fit, the best model for each species was used to forecast 1993 CPUEs using preliminary 1993 catch data. Estimated 1993 CPUEs were compared with the observed CPUEs. These comparisons were useful to validate the models. For 1994, both total catches and CPUEs were forecasted, again using the procedures in Bowerman and O'Connell (1993) and SAS Institute, Inc. (1993).
2.2 Data Sources
Three sets of fisheries data were used in this paper: (1) domestic total catch in kg from all gears used by the Hawaii domestic fisheries as reported to the Hawaii Department of Aquatic Resources (HDAR) from 1962 to 1992; (2) foreign longline catch by Japanese fishing vessels in the EEZ of the main Hawaiian Islands (Yong and Wetherall, 1980); (3) CPUE from the Hawaii domestic handline, longline, and trolling fisheries derived from the HDAR data for 1962 to 1992, hereafter referred to as CPUE. Total catch was calculated by summing domestic and foreign catches.
Previous studies (Hudgins and Pooley, 1987) reported that total catches from the HDAR data sets underestimated actual catches because some fishermen, especially longliners, failed to report their catches. To solve this problem, we compared HDAR catch data for various gears and ports of landing with data from fish dealers in the Hawaiian Islands (Pooley, NMFS, Honolulu, Hawaii, unpubl. data). Catches from the HDAR data sets were similar to the dealers' data for handline and trolling gears but were much lower than the dealers' data for longline gear, especially from the early to mid 1980s. We then calculated annual raising factors for longline gear based on the comparisons between the HDAR data and the dealers' data. Final estimates of total catches by the local fisheries used in this paper were then calculated from raised HDAR longline data plus the HDAR data for all other gears. Details on the estimation of these raising factors will be described in a separate report (Boggs, He, Yang and Curran, NMFS, Honolulu, Hawaii, unpubl. data).
Domestic longliners have extended their range beyond the Hawaii EEZ, especially as they began targeting swordfish (Xiphias gladius) during 1990-92. No correction of the domestic catch data was made for fish caught outside the EEZ. Domestic longliners that targeted tuna fished primarily within the EEZ during 1990-92.
Longliners from Japan were active in the Hawaii EEZ prior to April of 1980 after which, under new regulations, they chose not to fish. Total catches by Japan in the Hawaii EEZ from 1962 to April of 1980 were estimated using the same procedures as Yong and Wetherall (1980). These procedures included converting numbers of fish to weight using average weight statistics from Hawaii longline catches.
The CPUEs of both species were obtained from the HDAR data. Longline CPUEs were calculated as kg per trip and converted to kg per 1,000 hooks as described below. The CPUEs for the handline and troll fisheries were calculated as kg per trip. For bigeye tuna, because reported catches by handline and trolling were very low, only CPUEs from the longline fishery were calculated.
To calculate CPUE from the HDAR data, certain problematic records were first deleted. The following six procedures were applied:
(1) Incomplete records, such those with missing date, species names, type of gear, etc., were deleted.Because the HDAR data only provided total catch per trip, to convert longline CPUE to weight per 1000 hooks, the annual average numbers of hooks used per longline trip were estimated from other data sources (Boggs and Hawn, NMFS, Honolulu, Hawaii, unpubl. data).(2) Records from trips that used more than one fishing gear on a trip were deleted.
(3) Records that reported no catch of any species were deleted because such data were not consistently recorded before 1990.
(4) Records of handliners who fished at offshore seamount and weather buoy areas from 1989 to 1992 were deleted because the offshore handline fishery is distinct, and including these data in the analysis would bias the long-term trend of CPUE time series.
(5) Records of longliners from trips whose reporting intervals (presumably lengths of trip) were £ 3 days were deleted. These data probably represent landing over several days from single trips, or a group of longliners that conduct very short trips.
(6) Records of longliners from trips that presumably targeted swordfish (Xiphias gladius) from 1990 to 1992 were deleted. Identification of swordfish trips was done by applying cluster analysis on species composition data (% of total catch) from each trip. All trips that belonged to the cluster with the highest catch of swordfish were then deleted.
3. RESULTS
3.1 Bigeye Tuna
At the annual time scale, total catches of bigeye tuna by all gears fluctuated around 1,000 mt from 1962 to late 1970s (Figure 1). Total catches then dramatically declined from 1,504 mt in 1978 to 82 mt in 1981. Beginning in 1982, total catches steadily increased to around 1,700 mt in the early 1990s. The annual longline CPUE of bigeye tuna, however, showed a different pattern. CPUEs were the highest in the 1960s, fluctuating around 350 kg per 1,000 hooks, and then decreased to around 150 kg per 1,000 hooks in 1970s (Figure 1). Corresponding to the lowest total catch (all gears) in 1981, longline CPUE was zero in 1981. These longline data may reflect an unresolved under-reporting problem. From 1982 to 1992, CPUEs fluctuated around 120 kg per 1,000 hooks.
Figure 1. Annual total catch and catch per unit effort (CPUE) for bigeye tuna caught by the Hawaii longline fishery from 1962 to 1992.
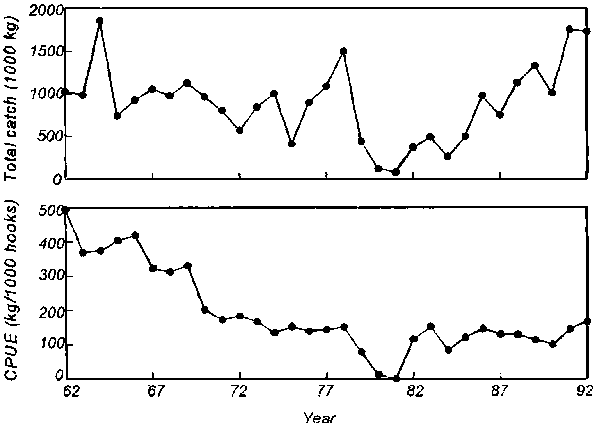
At the annual time scale, time series analysis indicated that total catches had no negative effects on CPUE. In other words, we found no evidence that CPUE was lower when catch was higher, at any lag. Instead, w terms in models (Table 1) indicated significant positive relationships between total catches and CPUE. Note that for example, Model 3, which included each of the lag terms found to be significant in Models 1 and 2, and fitted the data best, showed positive relationships at lags of 0 years (w0=0.000048) and at 5 years (w5=0.000051). In other words, when catch was higher, CPUE was higher during that year and 5 years later.
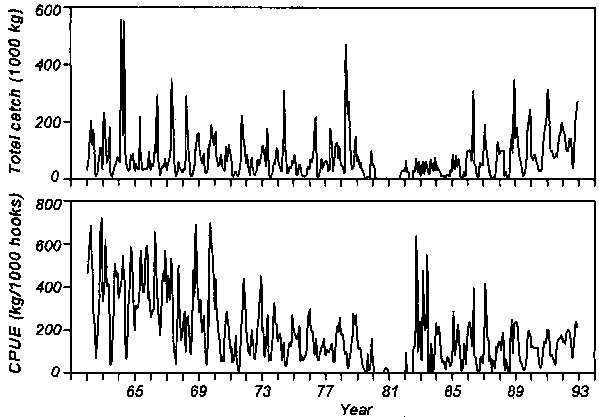
At the monthly time scale, both total catches and CPUE of bigeye tuna showed strong seasonality in all years except during the early 1980s when both catches and CPUE were the lowest (Figure 2). In general, high catches and CPUE occurred during the winter months; and within-year variability (i.e., seasonal change) was greater than between-year variability (i.e., annual change).
At the monthly time scale, time series analysis showed that total catches had a positive relationship with CPUE at a lag of 0 months (w0=0.00040, Model 1 in Table 1) and had a negative effect on CPUE at a lag of 2 months in another model with only slightly better fit (w2=-0.00020, Model 2 in Table 1).
Table 1. Parameter estimates of transfer functions relating total catches to catch per unit effort (CPUE) and residual models for bigeye tuna at annual and monthly time scales from 1962 to 1992. The input variable is total catch and the output variable is CPUE for the Hawaii longline fishery. Abbreviations are: b= delay parameter (see Equation 1); s.e. = standard error for the estimate; T ratio = T statistics for the estimate (|T ratio| > 1.96 indicates the estimate is significantly greater than zero with probability of 0.95); SBC = Schwartz's Bayesian Criterion, which measures goodness-of-fit. The smaller the value of SBC, the better the fit.
|
Model
|
Transfer function
|
T ratio |
Residual model
|
SBC
|
|||
|
b
|
Term
|
Estimate
|
s.e.
|
Order and estimate
|
|||
|
Annual scale
|
|||||||
|
Model 1
|
0
|
w0
|
0.000041
|
0.000018
|
2.29
|
AR: 1-0.49B2
|
319
|
|
Model 2
|
5
|
w0
|
0.000059
|
0.000018
|
3.25
|
None
|
257
|
|
Model 3
|
0
|
w0
|
0.000048
|
0.000019
|
2.50
|
|
|
| |
|
w5
|
0.000051
|
0.000017
|
3.02
|
None
|
254
|
|
Monthly scale
|
|||||||
|
Model 1
|
0
|
w0
|
0.00038
|
0.000076
|
5.02
|
AR: 1-0.74B1
|
|
| |
|
|
|
|
MA: (1-0.32B1+0.18B11)(1-0.78B12)
|
4360
|
|
|
Model 2
|
0
|
w0
|
0.00040
|
0.000075
|
5.31
|
|
|
| |
w2
|
-0.00020
|
0.000075
|
-2.68
|
AR: 1-0.75B1
|
|
|
| |
|
|
|
|
MA: (1-0.33B1+0.20B11)(1-0.79B12)
|
4335
|
|
Figure 2. Monthly total catch and catch per unit effort (CPUE) for bigeye tuna caught by the Hawaii longline fishery from 1962 to 1992.
3.2 Yellowfin Tuna
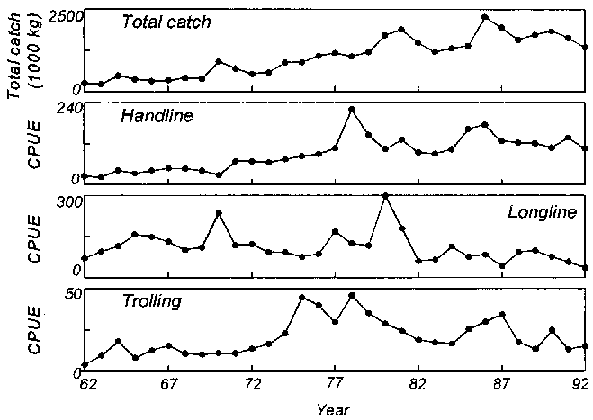
At the annual time scale, total catches of yellowfin tuna steadily increased from around 300 mt in the early 1960s to around 1,600 mt in the early 1990s with a peak of 2,265 mt in 1986 (Figure 3). The CPUE for handline gear showed an increasing trend similar to the total catch but with a peak in 1978 (Figure 3). The CPUE for both longline and trolling gears, however, showed different patterns from that of handline gear (Figure 3). The CPUE for longline gear fluctuated around 100 kg per 1,000 hooks prior to 1980 and fluctuated around 70 kg per 1,000 hooks after 1982. Longline CPUE had the highest CPUE values in 1970 and 1980. The CPUE for trolling gears was low from the 1960s to the early 1970s, high in the mid 1970s with a peak in 1978, and then deceased thereafter (Figure 3). The CPUE for trolling gear in the most recent years (1987 to 1992) was low and similar to the CPUE from the 1960s to the early 1970s.
At the annual time scale, time series analysis showed that total catches of yellowfin tuna had no effects on handline or trolling CPUE at any lags, since estimates of w were not significant (Table 2). However, total catches of yellowfin tuna had a positive relationship with longline CPUE at a lag of 0 years (w0=0.00012) and had negative effects at a lag of 1 year (w1=-0.000075) in Model 2 (Table 2).
Figure 3. Annual total catch and catch per unit effort (CPUE) for yellowfin tuna caught by the Hawaii handline, longline, and trolling fisheries from 1962 to 1992.
At the monthly time scale, time series of total yellowfin tuna catches and CPUE for three gears (Figure 4) showed similar patterns as those for bigeye tuna: strong seasonality with higher within-year variability than between-year variability. The differences between the bigeye and yellowfin tuna times series were that high catches and high CPUEs for yellowfin tuna occurred during the summer months instead of the winter months.
At the monthly time scale, time series analysis showed that total catches of yellowfin tuna had positive relationships with the CPUEs of all three gears at lag of 0 months, as all estimates of w0 were significantly positive (Table 2).
3.3 Comparisons of Observed, Estimated and Forecasted CPUE
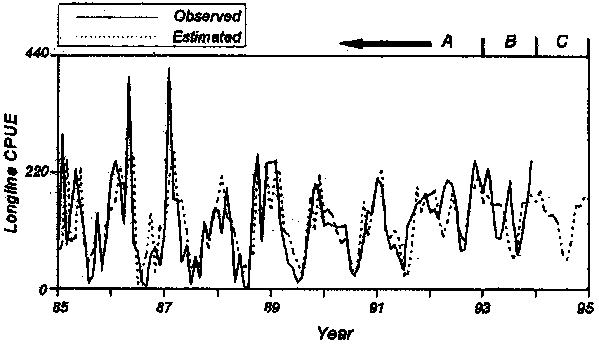
The time series of estimated CPUE (1985-92), CPUE forecasted by the transfer model (1993-94), observed CPUE for bigeye tuna caught by longline (1985 to 1992), and preliminary data for 1993 (Figure 5) showed that the estimated CPUE matched well with the observed CPUE, especially in terms of seasonal changes. In other words, the model was good at estimating when the peaks of CPUE should occur. In 1993, the CPUE forecasted using the total catch data showed similar seasonal changes, but failed to estimate an atypical peak in CPUE observed from June to August (Section B, Figure 5). The CPUE forecasted for 1994 without having total catch data showed the same seasonal changes as were estimated for 1993.
Table 2. Parameter estimates of transfer functions relating total catch to catch per unit effort (CPUE) and residual models for yellowfin tuna at annual and monthly time scales from 1962 to 1992. The input variables are total catches and the output variables are CPUE for handline, longline, and trolling, respectively. Abbreviations are same as in Table 1.
|
Model
|
Transfer function
|
Residual model
|
SBC
|
||||
|
B
|
Term
|
Estimate
|
s.e.
|
T ratio
|
Order and estimate
|
||
|
Annual scale, handline
|
|||||||
|
Model 1
|
0
|
w0
|
0.0000042
|
0.0000022
|
0.19
|
None
|
---
|
|
Annual scale, longline
|
|||||||
|
Model 1
|
0
|
w0
|
0.00011
|
0.000038
|
2.91
|
AR: 1+0.18B2
|
328
|
|
Model 2
|
0
|
w0
|
0.00012
|
0.000028
|
4.33
|
|
|
| |
w1
|
-0.000075
|
0.000027
|
-2.72
|
AR: 1+0.33B2+0.41B6
|
315
|
|
|
Annual scale, trolling
|
|||||||
|
Model 1
|
0
|
w0
|
-0.000094
|
0.000055
|
-1.70
|
None
|
|
|
Monthly scale, handline
|
|||||||
|
Model 1
|
0
|
w0
|
0.00049
|
0.000047
|
10.40
|
AR: 1-0.54B1
|
|
| |
|
|
|
|
MA: (1+0.19B11)(1-0.94B12)
|
---
|
|
|
Monthly scale, longline
|
|||||||
|
Model 1
|
0
|
w0
|
0.00072
|
0.00011
|
6.84
|
AR: 1-0.77B1
|
|
| |
|
|
|
|
MA: (1-0.45B1+0.23B7)(1-0.76B12)
|
---
|
|
|
Monthly scale, trolling
|
|||||||
|
Model 1
|
0
|
w0
|
0.00054
|
0.00012
|
4.38
|
AR: 1-0.87B1
|
---
|
| |
|
|
|
|
MA: (1-0.38B1-0.18B2+0.21B10)(1-0.82B12)
|
|
|
Figure 4. Monthly total catch and catch per unit effort (CPUE) for yellowfin tuna caught by the Hawaii handline, longline, and trolling fisheries from 1962 to 1992.
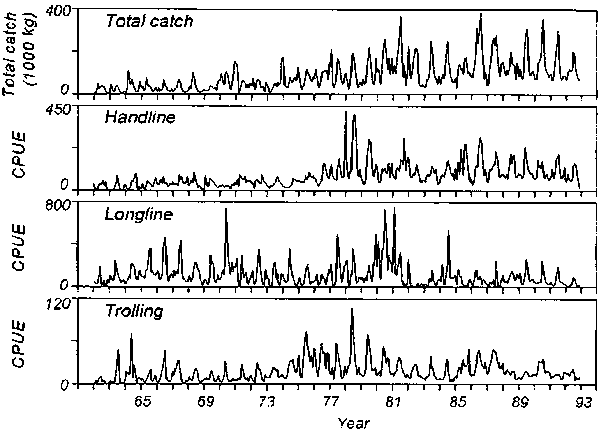
Figure 5. Monthly observed catch per unit effort (CPUE) for bigeye tuna caught by the Hawaii longline fishery from 1962 to 1992 (solid line, Section A and B), estimated CPUE from 1962 to 1992 (dashed line, Section A), forecasted CPUE using the input variable (total catch) in 1993 (dashed line, Section B), and CPUE forecasted without the input variable (dashed line, Section C).
Comparison of the time series of estimated and forecasted CPUE from the transfer models with the observed CPUE for yellowfin tuna caught by three gears (handline, longline, and trolling, Figure 6) generally showed that the estimates matched fairly well with the observed CPUE, especially for handline gear (Section A, Figure 6). Similar to the longline CPUE model for bigeye tuna, the three yellowfin tuna models estimated the seasonal changes well. Among the three gears, the estimated CPUE for handline matched best with the observed CPUE. The 1993-94 forecasted CPUE of three gears showed similar seasonal changes.
4. DISCUSSION
This paper addresses a question that has become a major concern of fishermen and management agencies in Hawaii: Do local catches affect local abundance of bigeye and yellowfin tuna? Prior to the inclusion of tunas in the US domestic fishery management regulations, similar questions were the subject of studies on managed species such as blue and striped marlin (Boggs, 1994). From the fisheries science viewpoint, these are not easy questions to answer. Rigorous answers require knowledge of exploited stock parameters such as catchability, availability, recruitment, natural mortality, and fishing mortality. Adequate estimation of such parameters may be very difficult or prohibitively expensive. Furthermore, the issue becomes much more complex as the stocks of both species are thought to be widely distributed. As Boggs (1994) pointed out, the troll CPUE of yellowfin tuna in Hawaii appeared not to be affected by domestic catches of yellowfin tuna, but was directly related to the apparent abundance of yellowfin tuna over a wide area of the central-western Pacific.
At present, information on stocks and movement patterns of both species around the Hawaiian Islands is not available, and will not likely be available in the near future. The best available data relevant to the question are long time series of Hawaii commercial fisheries statistics reported to HDAR. These may be inadequate to determine population parameters or true local abundance but we contend that they are useful for addressing the empirical question: Do local catches affect local CPUE?
The reliability of the HDAR data has been questioned by researchers and others aware of missing or inconsistent reports, misidentification of species, recording errors, and lack of data on unsuccessful trips. This analysis is a preliminary product of a project designed to intensively analyse the HDAR data and to account for problems with that data set. Our philosophy echoes the USA's federal management policy of using the best available data and our goal was to pose hypotheses that can be tested using the HDAR data.
The preliminary finding of this study is that we did not reject the null hypothesis that local catches have no effects on local abundance of both species. When fishing mortality is effectively reducing fish biomass, there should exist a negative relationship between catch and CPUE (Hilborn and Walters, 1992). However, we found no pattern of negative relationships. The positive relationships between catch and CPUE observed at the monthly time scale and zero lag for all fisheries does not imply that increasing catch caused CPUE to increase.
Positive relationships between catch and CPUE could result from lack of independence between catch and CPUE if both are calculated from the same data. We did not expect this to be the case in our analysis because we did not use same data to calculate both variables. Catch was the total from all domestic and foreign fisheries combined, whereas CPUE was calculated for individual domestic fisheries using a qualified subset of the data.
The two significant negative relationships found between local catches and CPUEs, one for bigeye tuna longline CPUE at a lag of two months and the other for yellowfin tuna troll CPUE at a lag of one year, did little to improve the fit of the transfer models. Consideration of multiple possible relationships dilutes the significance of these findings, and they do not seem to be part of any overall pattern of negative lag effects.
It is important to note that low CPUEs occurred when catches were low and numbers of fishing trips (presumably representing fishing effort) were low (Boggs and He, NMFS, Honolulu, unpubl. data). Fishermen may fish more when CPUE is higher than normal, and fish less when CPUE is lower than normal. The latter implies that local catches do not affect CPUE because fishing effort is reduced when CPUE declines, tending to prevent depletion of local abundance. A further analysis of fishing effort would be useful.
Catches and fishing effort are highly seasonal and correspond with seasons of high CPUE. For bigeye tuna total fishing effort is dominated by the longline fishery and peaks in winter. For yellowfin tuna total fishing effort is dominated by the troll and handline fisheries and peaks in summer. It remains to be seen if data on total effort would indicate positive correlations between differenced total effort and differenced CPUE. Such an analysis cannot be presented due to unresolved difficulties in quantifying total effort from the different fisheries.
Perhaps the most questionable assumption of this study is that changes in CPUEs represent changes in local fish abundance. Time series of CPUEs used in this study spanned over 30 years. It is undoubted that fishing techniques and fishermen's behaviour changed over this period. Therefore the catchability and fishing efficiency changed. Time series of CPUEs may include trends due to these changes, especially for handline and trolling gears whose CPUEs are measured as catch per fishing trip. At present, we cannot independently estimate these trends and remove them from the time series of CPUEs. What we did, however, was to detrend the time series by differencing, which removed long-term trends of changes in catchability and fishing efficiency together with long term trends in abundance, and emphasized short-term changes in CPUEs.
To remove some of the variations due to different fishing methods, our ongoing project is attempting to use multivariate analysis to cluster fishermen into subgroups based on their catch composition, their fishing expertise, and their fishing behavior. Time series of CPUEs estimated from these subgroups of fishermen will then be compared and used in future time series modelling. We are also attempting to model the damping effect on true variation in CPUE that is caused by the exclusion of data from unsuccessful fishing trips.
We expected that local catch would have, if any, more apparent relationships with local abundance at the monthly time scale than at the annual time scale, as was true for yellowfin tuna for both handline and trolling gears (Table 2). At the annual time scale, there were no significant relationships between catches and CPUEs for both handline and trolling gears, while at the monthly time scale, there existed positive relationships between catches and CPUEs for all gears. The prevalence of relationships at the monthly time scale is probably because (1) both species are thought to be highly mobile and widely distributed, and long-term trends in local abundance (i.e., years to decades) would be strongly affected by exogenous trends in the Pacific-wide stocks; (2) the immigration of fish to the local area appears to be highly seasonal, and strong seasonality in local abundance (i.e., from month to month) might exceed interannual variability; and (3) thus, the annual averages of CPUE would be much less sensitive to catches than the monthly averages of CPUE.
Time series analyses, especially transfer models, have not been commonly used in fisheries research (but see Cohen and Stone, 1987; Fogarty, 1988; Stergiou, 1989; Mendelssohn and Cury, 1989), mainly because time series analyses require long-term and stationary data that are often lacking. Hawaii fishery researchers are fortunate to have the HDAR data, which may have many problems but do contain much useful information on long-term and fine scale changes in Hawaii fisheries. This analysis demonstrates that time series models are applicable to the HDAR data, as shown by fairly good matches between observed and estimated CPUEs for both species and all gears. No useful alternative data are available for evaluating Hawaii troll and handline fisheries, nor are there any other data or information available for more traditional stock assessment. Time series modeling using HDAR data may be the most valuable tool available for studying Hawaii pelagic fisheries.
Future work will involve not only improving estimates of CPUEs by removing outliers from the data and by modeling distributions of CPUEs (Richards and Schnute, 1992; Perkins and Edwards, 1994), but also applying more advanced time series models, such as nonlinear transfer functions (Wei, 1990), multivariate time series models on multi-species catches (Cohen and Stone, 1987), Bayesian dynamics models that incorporated more recent data and more accurate data (i.e., federally mandated longline log data) (Pole et al., 1994) and spatially explicit time series models (Gillis et al., 1993).
5. ACKNOWLEDGMENTS
The data and data processing required to provide the starting point for this time series analysis were provided through the assistance of many including Reginald Kokubun at HDAR, Sam Pooley, Darryl Tagami, and Mike Quach at NMFS Honolulu Laboratory, and Quanhe Yang, Weining Wu, and Dan Curran at JIMAR. We thank Drs. Bob Skillman, Sam Pooley, Rick Deriso and John Hampton for their helpful comments on the early drafts. This work was funded, in part, by a cooperative agreement with the National Oceanic and Atmospheric Administration (Coop. Agr. No. NA37RJ0199) through the JIMAR Pacific Pelagic Fisheries Research Program. This paper is JIMAR Publication no. 95-283 and SOEST contribution no. 3895.
6. REFERENCES CITED
Boggs, C.H. 1994. Methods for analyzing interactions of limited-range fisheries: Hawaii's pelagic fisheries. In: Shomura, R.S, J. Majkowski and S. Langi (eds.). Interactions of Pacific Tuna Fisheries. Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 December 1991, Noumea, New Caledonia. Vol. 1: Summary report and papers on interaction. FAO Fish. Tech. Pap. (336/1): 74-91.
Boggs, C.H., and R.Y. Ito. 1993. Hawaii's pelagic fisheries. Mar. Fish. Rev. 55(2): 69-82.
Bowerman, B.L., and R.T. O'Connell. 1993. Forecasting and time series: An applied approach. Duxbury Press, Belmont, California.
Carpenter, S.R. 1993. Statistical analysis of the ecosystem experiments. In: Carpenter, S.R., and J.F. Kitchell (eds.). The trophic cascade in lakes. Cambridge University Press, New York, USA.
Cohen, Y., and J.N. Stone. 1987. Multivariate time series analysis of the Canadian fisheries system in Lake Superior. Can. J. Fish. Aquat. Sci. 44(Suppl.2): 171-181.
Fogarty, M.J. 1988. Time series models of the Maine lobster fishery: The effects of temperature. Can. J. Fish. Aquat. Sci. 45: 1145-1153.
Gillis, D.M., R.M. Peterman and A.V. Tyler. 1993. Movement dynamics in a fishery: Application of the ideal free distribution to spatial allocation of effort. Can. J. Fish. Aquat. Sci. 50(2): 323-333.
Hilborn, R., and C.J. Walters. 1992. Quantitative fisheries stock assessment. Chapman and Hall, New York, USA.
Hudgins, L.L., and S.G. Pooley. 1987. Growth and contraction of domestic fisheries: Hawaii's tuna industry in the 1980s. In: Doulman, D.J. (ed.). Tuna issues and perspectives in the Pacific islands region. East-West Center Press, Honolulu, Hawaii: 225-241.
Mendelssohn, R., and P. Cury. 1989. Fluctuations of a fortnightly abundance index of the Ivoirian coastal pelagic species and associated environmental conditions. Can. J. Fish. Aquat. Sci. 44: 408-421.
Miyabe, N. 1993. A review of the biology and fisheries for bigeye tuna, Thunnus obesus, in the Pacific Ocean. In: Shomura, R.S, J. Majkowski and S. Langi (eds.). Interactions of Pacific Tuna Fisheries. Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 December 1991, Noumea, New Caledonia. Vol. 2: Papers on biology and fisheries. FAO Fish. Tech. Pap. (336/2): 207-243.
Perkins, P.C., and E.F. Edwards. 1994. A mixture model for estimating bycatch from data with many zero observations: Tuna bycatch in the eastern tropical Pacific Ocean. NMFS SWFSC Admin. Rep. LJ-94-07: 28 p.
Pole, A., M. West, and J. Harrison. 1994. Applied Bayesian forecasting and time series analysis. Chapman and Hall, New York, USA.
Pooley, S.G. 1993. Hawaii's Marine Fisheries: Some history, long-term trends, and recent developments. Mar. Fish. Rev. 55(2): 7-19.
Richards, L.J., and J.T. Schnute. 1992. Statistical models for estimating CPUE from catch and effort data. Can. J. Fish. Aquat. Sci. 49: 1315-1327.
SAS Institute, Inc. 1993. SAS/ETS user's guide, Version 6, 2nd Edition, Cray, North Carolina, USA.
Skillman, R.A., C.H. Boggs and S.G. Pooley. 1993. Fishery interaction between the tuna longline and other pelagic fisheries in Hawaii. NOAA Tech. Memo. NMFS-SWFSC 189: 46 p.
Stergiou, K.I. 1989. Modelling and forecasting the fishery for pilchard (Sardina pilchardus) in Greek waters using ARIMA time-series models. J. Cons. Int. Explor. Mer. 46: 16-23.
Suzuki, Z. 1993. A review of the biology and fisheries for yellowfin tuna (Thunnus albacares) in the western and central Pacific Ocean. In: Shomura, R.S, J. Majkowski and S. Langi (eds.). Interactions of Pacific Tuna Fisheries. Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 December 1991, Noumea, New Caledonia. Vol.2: Papers on biology and fisheries. FAO Fish. Tech. Pap. (336/2): 108-137.
Wei, W.W.S. 1990. Time series analysis: Univariate and multivariate methods. Addison-Wesley Publishing Company, Redwood City, California, USA.
Yong, M.Y.Y., and J.A. Wetherall. 1980. Estimate of the catch and effort by foreign tuna longliners and baitboats in the fishery conservation zone of the central and western Pacific, 1965-77. NOAA Tech. Memo. NMFS-SWFC 2: 103 p.