Théorie de base et plan d'échantillonnage
SOMMAIRE
| 1. | Population, cadre, unités d'échantillonnage, unités d'enquête | |
| 2. | Méthode de sélection | |
| 2.1 | Echantillonnage aléatoire simple (EAS) | |
| 3. | Estimation de la moyenne de la population à partir d'un échantillon et précision de l'estimation | |
| 3.1 | Estimation de la population totale et précision | |
| 3.2 | Taille de l'échantillon | |
| 4. | Estimation des proportions et leurs usages | |
| 5. | Echantillonnage stratifié | |
| 5.1 | Taille de l'échantillon dans les strates | |
| 6. | Estimateurs rapport | |
| 7. | Echantillonnage à probabilités inégales | |
| 7.1 | Méthode de sélection | |
| 7.2 | Méthode d'estimation | |
| 8. | Echantillonnage à deux niveaux | |
| 8.1 | Sélection au hasard des unités du premier niveau | |
| 8.2 | Sélection des unités du premier niveau avec des probabilités proportionnelles | |
1. Population, cadre, unités d'échantillonnage, unités d'enquête
Chaque fois qu'on envisage de réaliser une enquête, il faut avant tout préciser les unités qui doivent y être incluses et leur contexte géographique. Tout échantillonnage rigoureux demandeune subdivision du matériel à échantillonner en unités appelées“unités d'échantillonnage” qui constituent la base du processus d'échantillonnage. Une définition claire et non ambigüe nécessite l'existence ou la constitution d'une liste (= cadre d'échantillonnage) des unités. Dans le cas d'une enquête pour l'évaluation des captures (pour les pêcheries traditionnelles et artisanales) la hiérarchie suivante peut être mise en place pour les unités d'échantillonnage:
- unités primaires (PSU): points de débarquement
- unités secondaires (SSU): unités économiques de pêche
Les éléments d'information sur les caractéristiques de l'enquête sont récoltés à partir des SSU qui sont aussi appelées “unités d'enquête”.
Pour la collecte des données, l'une des méthodes d'enquête suivantes peut être employée:
(a) la méthode du recensement. Celle-ci implique la description complète de la population enquêtée; dans une méthode par recensement l'information est obtenue à partirde toutes les unités d'enquête de la population; et
(b) la méthode par échantillonnage, par laquelle l'information est obtenue à partir d'une fraction correctement sélectionnée de la population. Dans les enquêtes à grande échelle, la sélection provient du cadre d'échantillonnage existant.
2. Sélection des unités d'échantillon
S'il y a N unités d'échantillonnage et que l'on désire réaliser un simple échantillon au hasard1 de taille n, on peut extraire tous les échantillons possibles de taille n et en choisir un au hasard. Le nombre d'échantillons de taille n qui sont susceptibles d'être sélectionnésdans une population N est:
1 Ceci signifie que chaque unité dans la population a une probabilité égale et non nulle d'être sélectionnée dans l'échantillon
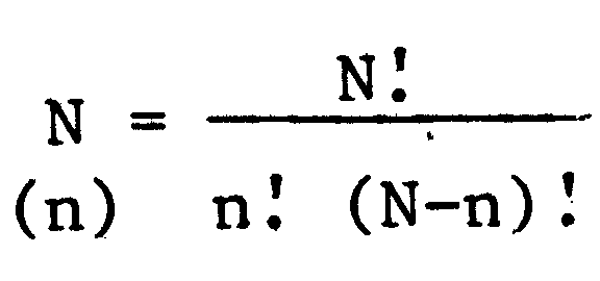
où: est le signe factoriel, par exemple, 3: = 1 × 2 × 3, etc. Si par exemple N = 4 et n = 2, le nombre d'échantillons distincts qui peuvent être sélectionnés est:
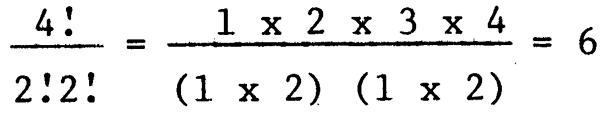
En pratique, quand N est grand, il est impossible d'énumérer tous les échantillons possibles et d'en choisir un. Normalement un simple échantillon au hasard est extrait unité par unitéLes unités sont marquées séquentiellement dans la population de l à N. On se réfère ensuite à une table de nombres au hasard (voir en annexe la table 1) et on extrait de cette table une série de n nombres compris entre l et N, en prenant soin de rejeter les nombres supérieurs à N et de ne pas faire apparaître plus d'une fois le même nombre dans la série. Les unités marquées dans la population par le nombre sélectionné dans la série constituent l'échantillon des nunités sélectionnées. Il a été démontré que cette méthode fournit des échantillons aléatoires simples.
Exemple
Il y a N = 28 points de débarquement dans un district. On désire un échantillon aléatoire de n = 5 points.
Comme N = 28 est un nombre de deux chiffres, on se réfère à toute racine de deux chiffres dans la table de nombres au hasard. En se référant à la première racine de ce type, on trouve la série suivante: 23, 5, 14, 38, 97, 11, 43, 93, 49, 36, 7, etc.
Sélectionnons à présent les nombres compris entre 1 et 28, jusqu'à ce que nous obtenions une série de 5 nombres. Cette série est: 23, 5, 14, 11 et 7.
Les points de débarquement marqués par ces nombres dans la population constituent notre échantillon.
3. Estimation de la moyenne de population à partir d'un échantillon et précision de l'estimation
S'il y a N unités dans la population et que l'on mesure une certaine caractéristique (y) de toutes les unités de la population, alors on a:

A présent, si nous tirons un échantillon de n unités parmi les N unités de la population, on peut définir:
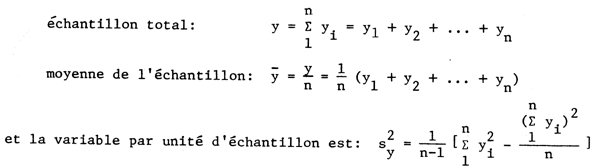
Si la même méthode de mensuration des caractéristiques désirées est employée à la fois pour les unités de population et pour les unités échantillon, la valeur absolue de la précision de la moyenne de l'échantillon est:
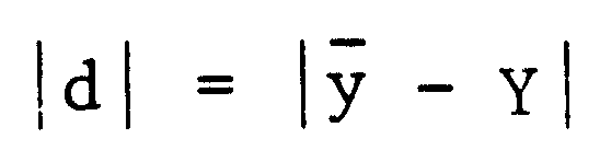
En général, la moyenne de la population  est inconnue et le but essentiel de l'échantillonnage
est d'obtenir une estimation de
est inconnue et le but essentiel de l'échantillonnage
est d'obtenir une estimation de  à partir de l'échantillon et également d'obtenir une mesure de la
précision de cette estimation. Nous savons que dans les EAS nous pouvons produire Ncn échantillons
Re
(de n unités) à partir d'une population de N unités et nous pouvons obtenir une série de moyennes
d'échantillons
à partir de l'échantillon et également d'obtenir une mesure de la
précision de cette estimation. Nous savons que dans les EAS nous pouvons produire Ncn échantillons
Re
(de n unités) à partir d'une population de N unités et nous pouvons obtenir une série de moyennes
d'échantillons  . Et (
. Et ( ) est égal à
) est égal à  , aussi
, aussi  est un estimateur non biaisé de
est un estimateur non biaisé de  . Il a aussi été
démontré que dans le cas d'une sélection par EAS, la variance de
. Il a aussi été
démontré que dans le cas d'une sélection par EAS, la variance de  est:
est:
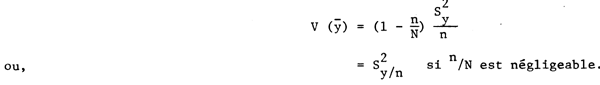
L'erreur standard de la moyenne de l'échantillon  est:
est:
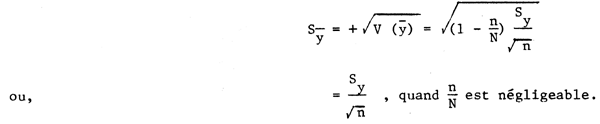
S mesure le degré de dispersion de la moyenne possible de l'échantillon autour de
mesure le degré de dispersion de la moyenne possible de l'échantillon autour de  . Plus
cette yaleur est faible, plus faible est la probabilité d'avoir une grande déviation de
. Plus
cette yaleur est faible, plus faible est la probabilité d'avoir une grande déviation de  parrapport
à
parrapport
à  . Pour n > 30, on a montré que pour un niveau de probabilité de 95% lamoyenne
. Pour n > 30, on a montré que pour un niveau de probabilité de 95% lamoyenne  de la population
se trouve dans un intervalle,
de la population
se trouve dans un intervalle,
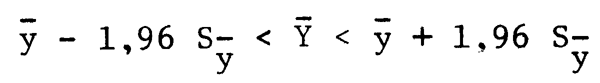
On voit donc que S fournit une mesure de la précision de l'évaluation.
fournit une mesure de la précision de l'évaluation.
On ignore en général S qui permettrait de calculer S
qui permettrait de calculer S . Dans les EAS, une estimation non
biaisée de S
. Dans les EAS, une estimation non
biaisée de S est fournie par s
est fournie par s .
.
Ainsi une estimation non biaisée de l'erreur standard de la moyenne de l'échantillon  est:
est:

3.1 Estimation de la population totale et précision
Dans un échantillon EAS, l'estimation de total de la population est donné par:

Exemple 3.la
En un point de débarquement, 30 bateaux mettent leurs captures à terre un certain jour et les prises (yi) de 10 d'entre eux choisis au hasard sont examinées. Evaluer la capture totale du jour ainsi que son erreur standard et son coefficient de variation: N = 30; n = 10.
| Bateau échantillonné | Captures (kg) | |
|---|---|---|
| yi | y²i | |
| 1 | 12 | 144 |
| 2 | 8 | 64 |
| 3 | 4 | 16 |
| 4 | 6 | 36 |
| 5 | 0 | 0 |
| 6 | 16 | 256 |
| 7 | 5 | 25 |
| 8 | 9 | 81 |
| 9 | 11 | 121 |
| 10 | 9 | 81 |
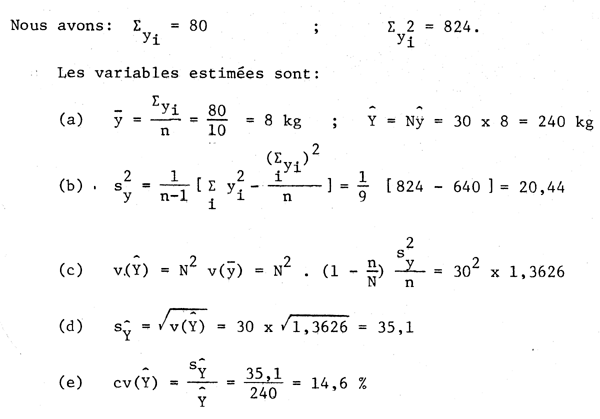

Alors, pour un grand N, au niveau de probabilité de 95 %, la moyenne de population se situera
entre l'intervalle  ± 1,96 s
± 1,96 s ou plus grossièrement entre
ou plus grossièrement entre  ± 2
± 2  . Cependant,
. Cependant,
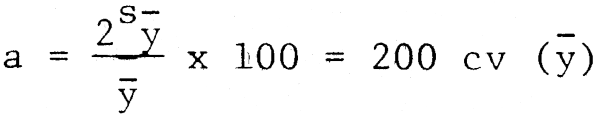
représente le pourcentage de précision de la moyenne au niveau de significativité de 5 %.
Ainsi, la taille d'échantillon n nécessaire pour une précision a% de la moyenne au niveau 5 % est fournie par:
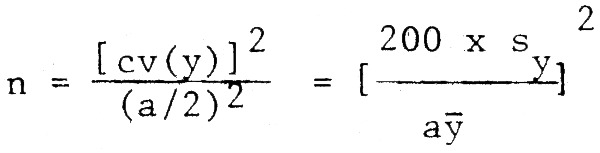
Exemple 3.2a
Dans une enquête, l'échantillon n = 18 a fourni une moyenne de  = 589,44 kg et sy = 531,79.
Combien d'unités seraient-elles nécessaires si on voulait évaluer avec un niveau de significativité
de 5 % la moyenne (a) à 10 %, (b) à 5 %, et (c) à 1 % de la moyenne de la population.
= 589,44 kg et sy = 531,79.
Combien d'unités seraient-elles nécessaires si on voulait évaluer avec un niveau de significativité
de 5 % la moyenne (a) à 10 %, (b) à 5 %, et (c) à 1 % de la moyenne de la population.

Exemple 3.2b
Dans l'exemple 3.la, si nous avions déduit une estimation de  avec un cv de 5 %, quelle aurait
été la taille de l'échantillon nécessaire?
avec un cv de 5 %, quelle aurait
été la taille de l'échantillon nécessaire?
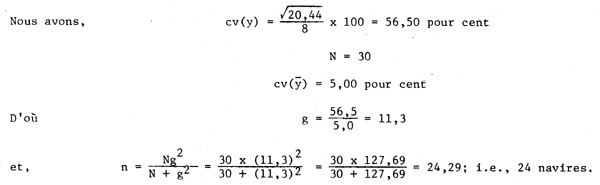
4. ESTIMATION DES PROPORTIONS ET LEURS USAGES
Soient N unités de la population, dont Ni appartiennent à la classe i, de telle manière que la proportion appartenant à la classe i soit: Pi = Ni/N On veut estimer Ni et Pi à partir d'un tirage aléatoire simple de n unités dans lequel ni se trouve dans la classe i, de telle sorte que: pi = ni/n.
On a yu qu'une estimation non biaisée  i de Pi est fournie par pi, de telle manière que
i de Pi est fournie par pi, de telle manière que
 i = pi = ni/n, et qu'une estimation non biaisée de Ni (où i est le nombre dans la classe i de la
population) est fournie par:
i = pi = ni/n, et qu'une estimation non biaisée de Ni (où i est le nombre dans la classe i de la
population) est fournie par:  i = N.pi.
i = N.pi.
Une estimation non biaisée de la variance de pi est:
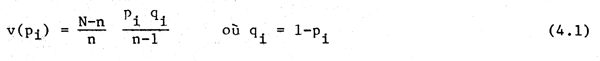
Quand n/N est petit, c'est-à-dire lorsque n est beaucoup plus petit que N ou que N est très grand, on a:
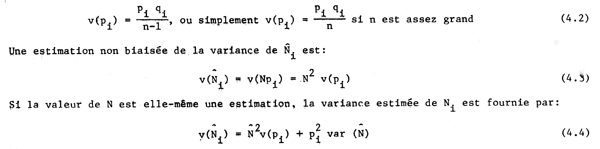
Exemple 4.1
Un échantillon au hasard de 82 navires a été tiré d'un ensemble de 820 navires, dont 32 employaient des lignes. Evaluer la proportion de navires ligneurs.
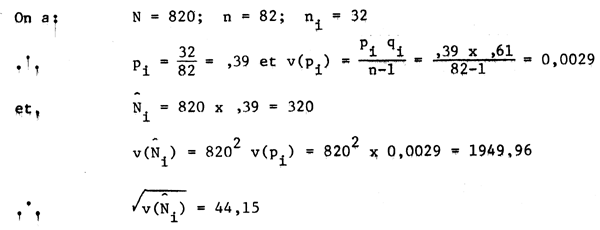
Exemple 4.2
Deux milles morues ont été débarqvées. Un échantillon de 100 morues a été prélevé et leurs âges déterminés. Leur distribution est la suviante:
Age | 8 | 9 | 10 | 11 | 12 | Total |
Nombre (ni) | 14 | 54 | 7 | 19 | 6 | 100 |
Calculer les estimations du nombre de morues de chaque groupe d'âge dans le débarquement total et la variance de ces estimations.
On a ici: N = 2 000; n = n, + n2 + n3 + n4 + n5 = 100
| Age | 8 | 9 | 10 | 11 | 12 | Total |
|---|---|---|---|---|---|---|
| ni | 14 | 54 | 7 | 19 | 6 | 100 |
| Pi | ,14 | ,54 | ,07 | ,19 | ,06 | |
| qi | ,86 | ,46 | ,93 | ,81 | ,94 | |
| Pi qi | ,12 | ,25 | ,07 | ,15 | ,06 | |
 | ,0012 | ,0025 | ,0007 | ,0015 | ,0006 | (équation 4.2 si n est grand) |
| 280 | 1 080 | 140 | 380 | 120 | ||
| 4 800 | 10 000 | 2 800 | 6 000 | 2 400 | ||
| 69,3 | 100,0 | 52,9 | 77,4 | 49,0 |
5. ECHANTILLONNAGE STRATIFIE
On a vu que dans l'échantillonnage aléatoire simple, la variance de la moyenne v( ) dépend en
dehors de la taille de l'échantillon n, de la variabilitédes caractéristiques de la population,
c'est-à-dire de S²y. Si la population est hétérogène, c'est-à-dire si les mensurations varient
considérablement d'une unité à l'autre, il est possible en employant des observations auxiliaires
de la subdiviser en sous-populations (ou strates) dont chacune est homogène.
) dépend en
dehors de la taille de l'échantillon n, de la variabilitédes caractéristiques de la population,
c'est-à-dire de S²y. Si la population est hétérogène, c'est-à-dire si les mensurations varient
considérablement d'une unité à l'autre, il est possible en employant des observations auxiliaires
de la subdiviser en sous-populations (ou strates) dont chacune est homogène.
Supposons que nous ayons N unités dans la population et que celles-ci sont stratifiées en k strates avec Ni unités dans la énième strate. Tirons un échantillon de n unités, parmi lesquelles ni proviennent de la ième strate. Soit yij la mesure de la jème unité dans la énième strate.

Exemple 5
Parmi les 200 bateaux d'un district, 70 ont été engagés dans la pêche à la ligne, 120 dans la pêche au filet maillant, et 10 dans la pêche à la senne de plage. Dans le but d'évaluer la capture, 5 bateaux ligneurs, 7 pêchant au filet et 3 senneurs ont été sélectionnés et leurs captures en tonnes pour le mois de janvier ont été les suivantes:
Ligneurs: | 2, 3, 4, 5, 6 |
Filets: | 7, 8, 9, 10, 12, 13, 11 |
Senneurs: | 20, 23, 26 |
Quelle est la capture totale estimée pour janvier et la variance de cette estimation? Quelle est la prise moyenne par bateau et sa variance?
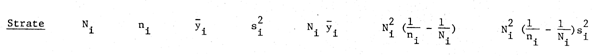
| 1 | 70 | 5 | 4 | 2,50 | 280 | 910 | 2 275,00 |
| 2 | 120 | 7 | 10 | 4,67 | 1 200 | 1 937,14 | 9 046.44 |
| 3 | 10 | 3 | 23 | 9,00 | 230 | 23,33 | 209,97 |
| Total | 200 | 15 | - | - | 1 710 | - | 11 530,97 |
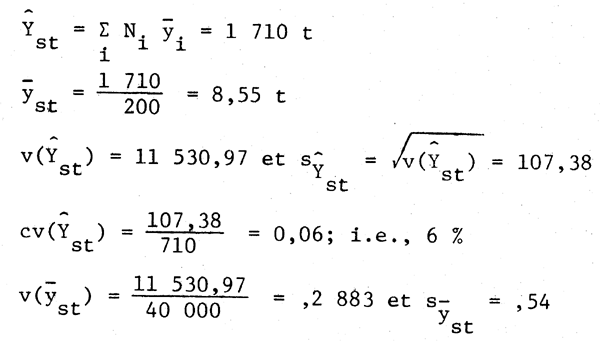
| Note: | S'il n'y avait pas de stratification et que nous avions choisi une série aléatoire simple de 15 unités dont les captures étaient semblables à celles de l'exemple 5, on aurait eu: |
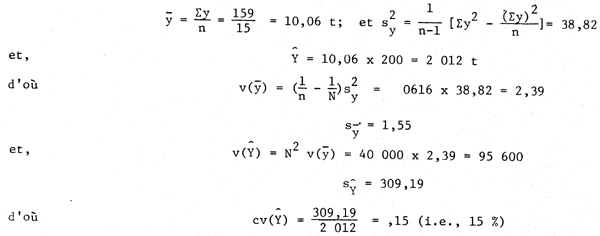
Plus clairement, nous avons obtenu, par stratification, une estimation dont le cv(Ŷ) est plus faible que dans le cas d'un tirage aléatoire simple.
5.1 Taille de l'échantillon dans les diverses strates
Dans l'exemple 5, on a sélectionné un échantillon de 15 unités et l'allocation du nombre d'unités dans les diverses strates a été faite arbitrairement.
Par ailleurs, lorsque la fraction d'échantillonnage est négligeable, on sait d'après l'équation (5.5) que la variance du total de la population s'exprime par:
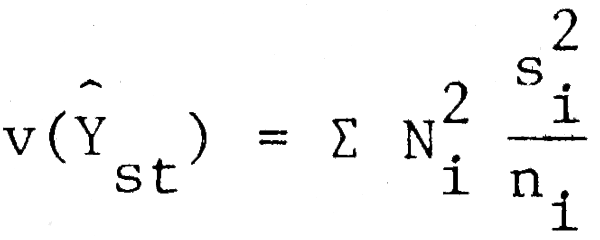
Cette équation suggère deux méthodes d'allocation de n entre les diverses strates:
(a) Allocation proportionnelle
Dans cette méthode, ni est proportionnel à Ni. Si les variances intra-strates sont égales, la méthode fournit la plus petite variance d'échantillonnage c'est-à-dire l'estimation la plus efficace. En général on emploie l'allocation proportionnelle quand l'information sur les variances des strates n'est pas disponible.
(b) Allocation optimale
Quand les variances intra-strates sont très différentes d'une strate à l'autre, l'allocation proportionnelle ne permet plus d'obtenir les meilleures estimations. Dans ce cas, il est préférable que la fraction d'échantillonnage soit prise en proportion de l'écart-type de la strate.
Pour plus de détails, se référer aux ouvrages sur les plans d'échantillonnage (Yates, Bazigos, 1974).
Exemple 5.1
Les captures suivantes proviennent de 18 traits échantillonnés au cours d'une enquête sur le chalutage:
| 200, | 440, | 600, | 640, | 700, | 800, | 900, | 1 020, | 1 600, | 1 920 |
| 20, | 10, | 340, | 400, | 720, | |||||
| 40, | 100, | 160 |
(a) Si le chalut a couvert 40 ha par trait et si 50 % du poisson se trouvant sur cette aire ont été capturés et que l'aire totale couverte par l'enquête était de 6 × 106 ha, estimer l'abondance totale du poisson.
(b) Si les 10 premiers traits, ont été effectués à des profondeurs de 0 à 20 m, les 5 suivants entre 20 et 40 m et les trois derniers à plus de 40 m, et que les surfaces des zones correspondant à ces profondeurs sont de 1 × 106, 2 × 106 et 3 × 106, quelle est alors l'abondance estimée?
(c) Calculer les variances des deux estimations ci-dessus.
Solution
(a) Echantillon non stratifié
Soit  la capture moyenne, si a est la surface balayée par chaque trait, la prise à l'hectare
est
la capture moyenne, si a est la surface balayée par chaque trait, la prise à l'hectare
est  /a. Etant donné que le filet ne capture que 50 %, c'est-à-dire que le coefficient de capturabilité
q est de 1/2, la densité à l'hectare du stock est:
/a. Etant donné que le filet ne capture que 50 %, c'est-à-dire que le coefficient de capturabilité
q est de 1/2, la densité à l'hectare du stock est:  divide;aq.
divide;aq.
D'autre part, les estimations d'abondance pour l'ensemble A sont:
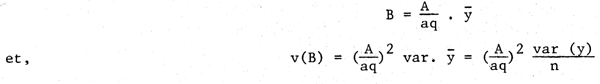
où n est le nombre d'échantillons de traits.

Les calculs numériques peuvent être convenablement exécutés sous forme de tableau:
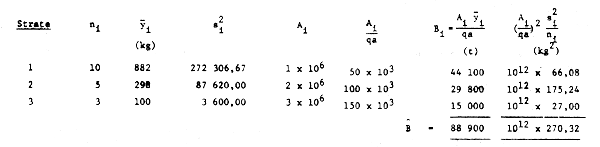
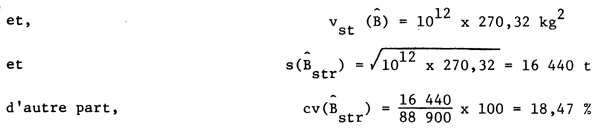
6. ESTIMATEUR RAPPORT
Il s'agit d'une autre méthode dans laquelle on emploie des informations auxiliaires pour augmenter la précision. Supposons que nous ayons sélectionné au hasard n unitês parmi N unités dans la population et que pour chacune des unités sélectionnées nous ayons mesuré(x, y) où y est la variable enquête et x est une autre variable corrélée. La population totale des variables x est:

mais y doit être connu pour chaque unité de la population, sauf pour celles qui composent l'échantillon.
Dans ce cas une estimation du total de la population Y de la variable enquête est fournie par:
Ŷrat = 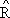 ×, où l'estimation de R est obtenue à partir de l'échantillon de la manière suivante:
×, où l'estimation de R est obtenue à partir de l'échantillon de la manière suivante:
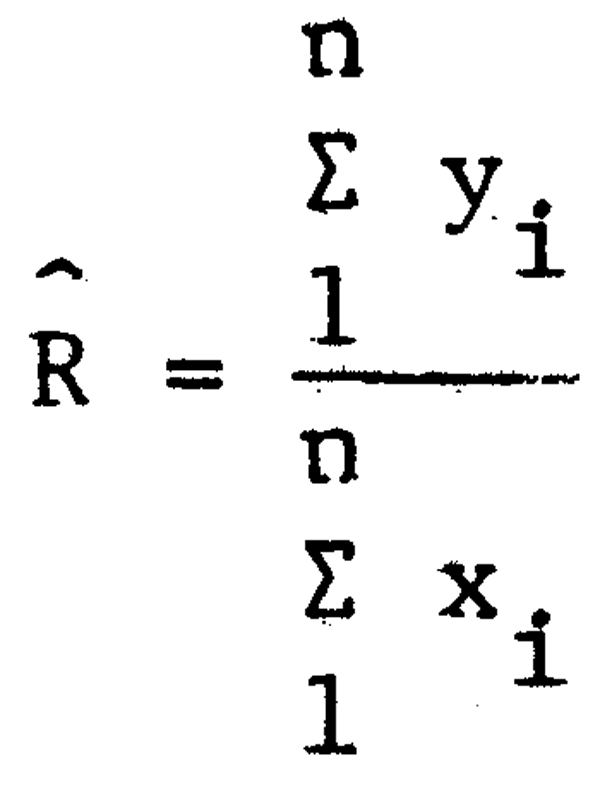
La variance de l'estimateur rapport Ŷrat est fournie par:
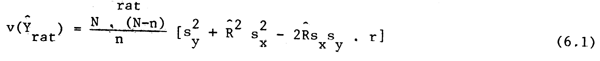
où r est l'estimation du coefficient de corrélation entre x et y.
Exemple 6.1
Dans un pays, il y a 50 centres de mise à terre où débarquent des creventtiers. Ces navires sont enregistrés et levr nombre total d'après les registres officiels est de 280. Cinq centres de débarquement sont sélectionnés au hasard et la capture (y) ainsi que le nombre de bateaux (x) dans chacun des cinq centres sont relevés. Calculer l'estimateur rapport des débarquements totaux des crevettiers dans le pays.
On a,
| Centres de débarquement: | Total - N = 50 | |
| Echantillon - n = 5 | ||
| Chalutiers: | Total - Y = 280 |
On a,
| Echantillon de centres débarquement | Nombre de chalutiers (x) | Prise (y) (t) | x² | y² | xy |
|---|---|---|---|---|---|
| 1 | 2 | 22 | 4 | 484 | 44 |
| 2 | 10 | 95 | 100 | 9 025 | 950 |
| 3 | 7 | 62 | 49 | 3 844 | 434 |
| 4 | 3 | 33 | 9 | 1 089 | 99 |
| 5 | 8 | 83 | 64 | 6 889 | 664 |
Total: | 30 | 295 | 226 | 21 331 | 2 191 |
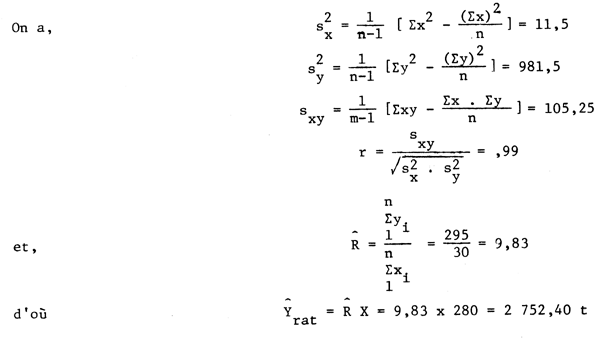
et d'après l'équation (6.1),
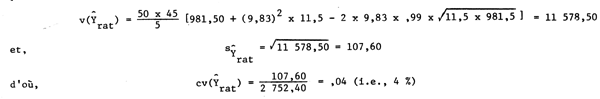
7. ECHANTILLONNAGE A PROBABILITES INEGALES
On a vu que par stratification et utilisation d'estimateurs-rapports on peut augmenter la précision des évaluations. Une autre technique employée dans ce but est l'échantillonnage proportionnel (PPS) dans lequel les unités d'échantillonnage sont sélectionnées avec des probabilités proportionnelles à leurs tailles. Cette méthode est largement utilisée dans les cas où l'on préfère échantillonner des groupes plutôt que des unités individuelles, ceci parce qu'il est plus économique d'échantillonner un nombre déterminé d'unités individuelles quand elles sont groupées et que parfois on ne dispose pas d'un schéma fiable des unités individuelles.
7.1 Méthode de sélection
Supposons que l'on ait 10 points de débarquement. Le nombre de navire dans chaque point figure dans la colonne 2. Nous voulons sélectionner 3 points par la méthode des probabilités proportionnelles.
| Lieu de débarquement | N° de navires | Total cumulé | Lots de nombres | N° sélectionné au hasard ou lieu de pêche |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) |
| 1 | 12 | 12 | 001–012 | |
| 2 | 5 | 17 | 013–017 | Nb hasard N° 011 |
| 3 | 20 | 37 | 018–037 | Lieu de pêche 01 |
| 4 | 2 | 39 | 038–039 | Nb hasard N° 027 |
| 5 | 30 | 69 | 040–069 | Lieu de pêche 03 |
| 6 | 15 | 84 | 070–084 | Nb hasard N° 064 |
| 7 | 8 | 92 | 085–092 | Lieu de pêche 05 |
| 8 | 6 | 98 | 093–098 | |
| 9 | 8 | 106 | 099–106 | |
| 10 | 14 | 120 | 107–120 | |
| 120 |
La colonne 3 est le total cumulé. Attribuons à présent à chaque point de débarquement un nombre proportionnel à sa taille. Ainsi le point l reçoit un lot de 12 nombres, de 001 à 012, le point 5 un lot de 30 nombres de 040 à 069 et ainsi de suite. Puis nous employons la table de nombre au hasard et sélectionnons 3 nombres entre l et 120. Ces nombres sont: 011, 027 et 064. Les lieux de pêche sélectionnés qui leur correspondent sont: 01, 03 et 05.
Il faut noter que dans cette méthode de sélection, une unité de grande taille a plus de chance d'être sélectionnée qu'une unité de petite taille.
7.2 Méthode d'évaluation
Soient N unités primaires d'échantillonnage (lieux de pêche) et xi le nombre d'unités secondaires (navires) dans le énième point de débarquement. Si n unités primaires sontsélectionnées par pps, la probabilité de tirer la énième unité dans l'échantillon est:
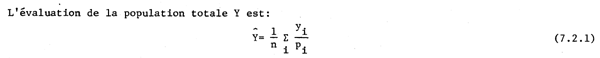
dans laquelle yi est la mesure de la énième unité dans l'échantillon; et la variance estimée de Y est donnée par:
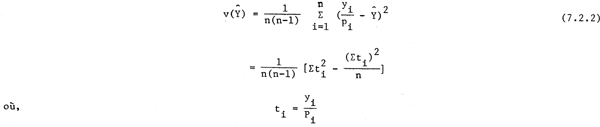
Exemple 7.2
Il y a 20 lieux de pêche dans un district. Le nombre de navires dans chaque centre est connu, par exemple, xi = nombre de navires dans le énième centre et par ailleurs X = ∑xi est égal à 496. Quatre lieux de pêche sont sélectionnés parmi les 20 par pps. Dans le tableau suivant, la colonne l donne les 4 lieux sélectionnés, la colonne 2 le nombre de navires (x) dans ces lieux et la colonne 3 les débarquements respectifs durant un mois. Estimez les débarquements mensuels totaux Ŷ et v (Ŷ).
| Sites | N°navires | Débarquements (en t) | p1 = xi/X | ti = yi/pi | t² |
|---|---|---|---|---|---|
| (xi) | (yi) | ||||
| (1) | (2) | (3) | (4) | (5) | (6) |
| 1 | 22 | 81 | 0,0443 | 1 828 | 3 341 584 |
| 2 | 30 | 118 | 0,0605 | 1 950 | 3 802 500 |
| 3 | 30 | 118 | 0,0605 | 1 950 | 3 802 500 |
| 4 | 42 | 170 | 0,0847 | 2 007 | 4 028 049 |
| Total: | 7 735 | 14 974 633 |

8. ECHANTILLONNAGE A DEUX NIVEAUX
Dans l'échantillonnage à deux niveaux, un échantillon d'unités de premier niveau est d'abord choisi, et dans chacune des unités primaires sélectionnées un échantillon d'unités d'enquête est choisi. On peut faire un simple choix au hasard pour les unités primaires, ou bien les sélectionner avec des probabilités égales à leurs tailles.
8.1 Sélection au hasard des unités primaires (SRS)
Soit:
N = Nombre d'unités primaires
n = Nombre d'échantillon d'unités primaires
Mi = Nombre d'unités d'enquête dans la énième unitéprimaire
mi = Nombre d'unités d'enquête sélectionnées dans la énième unité primaire
fi = n/M = Fraction d'échantillonnage primaire
f2i = mi/Mi = Fraction d'échantillonnage secondaire dans la ênième unité primaire
L'évaluation non biaisée de la population totale de la caractéristique (y) enquêtée est donnée
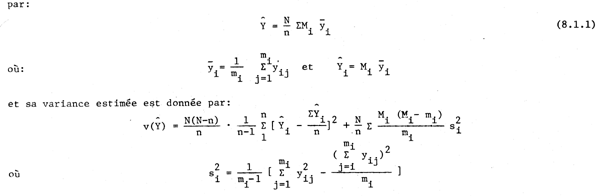
Exemple 8.1
Soient 8 lieux de pêche (N = 8). On sélectionne d'abord n = 3 lieux au hasard et pour chacun on sélectionne 3 casiers et on mesure leur capture. Le nombre de casiers qui se trouvent dans chacun des lieux sélectionnés et les prises de chaque casier sélectionné figurent dans le tableau qui suit. Calculez la capture totale estimée de la pêcherie et sa variance.
| Lieux d'échantillonnage | 1 | 2 | 3 |
| Nombre de casiers dans chaque lieu (Mi) | 6 | 9 | 7 |
| Nombre de casiers sélectionnés (mi) | 3 | 3 | 3 |
| Captures des casiers sélectionnés | 13 | 5 | 12 |
| 9 | 7 | 8 | |
| 6 | 10 | 13 | |
| Echantillon total | 28 | 22 | 33 |
| s²i | 12,3 | 6,3 | 7,0 |
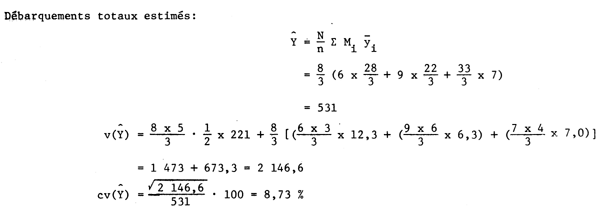
Il faut noter que la contribution 1 473,3 à v(Ŷ) est due à la différence entre les captures obtenues entre les lieux de pêche et qu'elle est bien supérieure à 673,3, ce qui est dû à la différence entre les unités secondaires à l'intérieur des unités primaires.
8.2 Sélections d'unités primaires par PPS
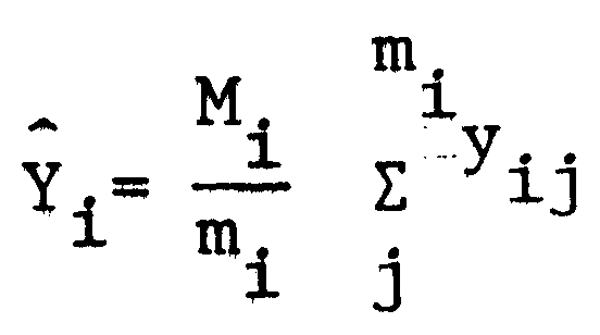
La capture estimée dans le énième lieu de pêche est:
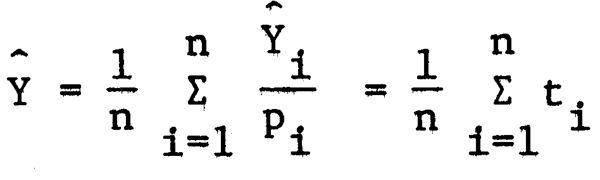
L'estimation non biaisée de la population totale est:
La variance de Y est:
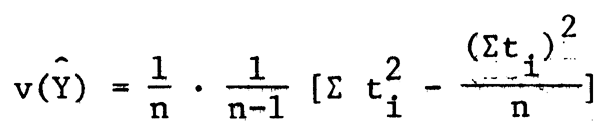
Exemple 8.2
Trois lieux de pêche ont été choisis par pps et dans chacun un échantillon simple de navires a été sélectionné au hasard. Le tableau suivant donne les captures (en kg) des échantillons sélectionnés. Calculez Ŷ et cv(Ŷ).

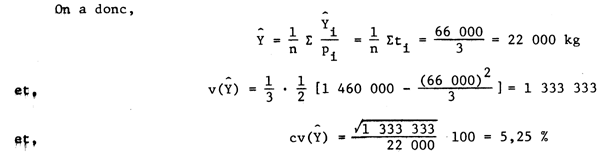
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 13 | 70 | 43 | 69 | 38 | 81 | 87 | 42 | 12 | 20 | 41 | 15 |
| 26 | 99 | 82 | 78 | 99 | 05 | 22 | 99 | 52 | 32 | 80 | 91 |
| 72 | 53 | 95 | 81 | 07 | 98 | 14 | 74 | 52 | 58 | 73 | 10 |
| 22 | 08 | 08 | 68 | 37 | 16 | 36 | 62 | 20 | 02 | 35 | 98 |
| 21 | 61 | 90 | 53 | 85 | 72 | 86 | 94 | 87 | 18 | 50 | 11 |
| 47 | 38 | 55 | 66 | 50 | 96 | 96 | 78 | 34 | 45 | 52 | 78 |
| 96 | 68 | 13 | 07 | 31 | 29 | 70 | 09 | 16 | 66 | 81 | 09 |
| 45 | 92 | 93 | 44 | 87 | 72 | 26 | 75 | 82 | 31 | 72 | 69 |
| 78 | 85 | 71 | 45 | 32 | 16 | 57 | 91 | 52 | 05 | 93 | 20 |
| 51 | 99 | 50 | 88 | 62 | 54 | 90 | 51 | 01 | 39 | 18 | 70 |
| 67 | 62 | 30 | 02 | 88 | 17 | 37 | 25 | 42 | 86 | 00 | 32 |
| 03 | 08 | 89 | 77 | 12 | 41 | 15 | 25 | 52 | 30 | 93 | 11 |
| 45 | 10 | 04 | 66 | 94 | 70 | 33 | 74 | 97 | 23 | 40 | 97 |
| 62 | 48 | 46 | 97 | 04 | 36 | 31 | 27 | 29 | 84 | 85 | 35 |
| 59 | 59 | 33 | 63 | 53 | 43 | 60 | 30 | 15 | 81 | 67 | 59 |
| 72 | 63 | 67 | 17 | 24 | 55 | 68 | 32 | 24 | 80 | 13 | 92 |
| 46 | 28 | 15 | 70 | 28 | 98 | 53 | 36 | 03 | 89 | 83 | 74 |
| 21 | 03 | 09 | 16 | 31 | 48 | 05 | 10 | 98 | 62 | 14 | 15 |
| 84 | 82 | 53 | 39 | 92 | 14 | 07 | 84 | 04 | 01 | 66 | 17 |
| 75 | 68 | 40 | 90 | 39 | 95 | 46 | 10 | 94 | 68 | 39 | 10 |
| 42 | 77 | 29 | 80 | 73 | 38 | 92 | 11 | 81 | 72 | 50 | 88 |
| 63 | 55 | 09 | 84 | 66 | 56 | 92 | 13 | 97 | 14 | 87 | 27 |
| 54 | 29 | 70 | 14 | 85 | 95 | 79 | 72 | 77 | 48 | 57 | 92 |
| 42 | 97 | 50 | 61 | 19 | 55 | 38 | 55 | 85 | 57 | 85 | 08 |
| 52 | 30 | 47 | 73 | 26 | 54 | 18 | 05 | 75 | 92 | 95 | 08 |
| 88 | 44 | 33 | 02 | 47 | 97 | 47 | 04 | 12 | 38 | 93 | 25 |
| 49 | 91 | 93 | 73 | 14 | 15 | 01 | 47 | 02 | 70 | 30 | 96 |
| 45 | 42 | 46 | 06 | 93 | 60 | 41 | 09 | 31 | 29 | 52 | 49 |
| 50 | 69 | 74 | 10 | 51 | 89 | 66 | 51 | 57 | 21 | 54 | 95 |
| 18 | 56 | 73 | 16 | 02 | 87 | 41 | 05 | 13 | 87 | 13 | 61 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 76 | 96 | 85 | 27 | 81 | 21 | 75 | 39 | 43 | 77 | 80 | 81 |
| 38 | 51 | 09 | 17 | 41 | 85 | 13 | 20 | 66 | 59 | 22 | 20 |
| 40 | 91 | 90 | 51 | 74 | 23 | 54 | 88 | 84 | 12 | 16 | 77 |
| 44 | 53 | 23 | 87 | 91 | 53 | 86 | 97 | 42 | 80 | 83 | 37 |
| 31 | 25 | 22 | 30 | 16 | 17 | 32 | 34 | 00 | 07 | 25 | 52 |
| 36 | 35 | 20 | 92 | 81 | 12 | 15 | 28 | 42 | 98 | 67 | 52 |
| 36 | 12 | 17 | 03 | 83 | 93 | 48 | 64 | 50 | 32 | 57 | 94 |
| 25 | 51 | 40 | 74 | 85 | 16 | 86 | 09 | 22 | 62 | 06 | 38 |
| 72 | 38 | 33 | 97 | 36 | 58 | 90 | 91 | 23 | 91 | 19 | 04 |
| 17 | 20 | 75 | 03 | 85 | 53 | 06 | 41 | 29 | 78 | 51 | 15 |
| 75 | 57 | 37 | 77 | 67 | 60 | 70 | 44 | 56 | 91 | 03 | 49 |
| 12 | 47 | 35 | 37 | 15 | 17 | 96 | 24 | 95 | 08 | 39 | 55 |
| 73 | 67 | 55 | 64 | 16 | 38 | 58 | 74 | 29 | 71 | 49 | 62 |
| 16 | 02 | 29 | 14 | 16 | 78 | 44 | 49 | 34 | 05 | 46 | 96 |
| 48 | 98 | 13 | 29 | 19 | 71 | 98 | 71 | 19 | 51 | 86 | 82 |
| 73 | 65 | 42 | 09 | 39 | 92 | 56 | 68 | 36 | 54 | 55 | 46 |
| 22 | 96 | 06 | 41 | 55 | 75 | 08 | 62 | 55 | 19 | 15 | 15 |
| 57 | 26 | 11 | 28 | 98 | 16 | 85 | 39 | 67 | 49 | 02 | 30 |
| 47 | 76 | 60 | 92 | 22 | 79 | 70 | 66 | 78 | 13 | 97 | 42 |
| 31 | 80 | 30 | 86 | 08 | 54 | 39 | 88 | 38 | 46 | 74 | 21 |
| 91 | 55 | 48 | 36 | 26 | 40 | 17 | 70 | 39 | 94 | 05 | 76 |
| 83 | 70 | 10 | 91 | 20 | 64 | 12 | 33 | 15 | 59 | 43 | 28 |
| 28 | 35 | 53 | 14 | 30 | 57 | 07 | 34 | 09 | 56 | 26 | 81 |
| 86 | 91 | 62 | 94 | 83 | 96 | 96 | 17 | 02 | 10 | 89 | 71 |
| 24 | 86 | 86 | 52 | 67 | 59 | 63 | 22 | 28 | 76 | 43 | 45 |
| 43 | 73 | 70 | 73 | 19 | 41 | 04 | 60 | 25 | 42 | 09 | 50 |
| 52 | 69 | 34 | 01 | 65 | 33 | 19 | 62 | 22 | 41 | 29 | 65 |
| 01 | 15 | 92 | 69 | 53 | 78 | 68 | 58 | 74 | 08 | 05 | 11 |
| 94 | 46 | 83 | 72 | 49 | 19 | 98 | 09 | 56 | 83 | 25 | 40 |
| 44 | 42 | 06 | 32 | 95 | 17 | 32 | 67 | 80 | 84 | 09 | 69 |
| 81 | 58 | 85 | 33 | 16 | 11 | 87 | 12 | 17 | 39 | 12 | 11 |
| 60 | 25 | 84 | 42 | 22 | 94 | 38 | 96 | 52 | 03 | 38 | 97 |
| 53 | 12 | 75 | 59 | 76 | 42 | 73 | 48 | 95 | 57 | 51 | 31 |
| 02 | 68 | 01 | 17 | 09 | 00 | 38 | 12 | 31 | 52 | 22 | 24 |
| 09 | 68 | 53 | 92 | 82 | 11 | 96 | 03 | 47 | 31 | 35 | 59 |