

This paper presents a model for evaluating agricultural production that incorporates agriculturally induced resource externalities. A two step calibration procedure is presented to parameterize multi-crop, multi-input production models. First a programming model is presented which uses existing market information and observed economic activity to estimate unobserved (shadow) costs to the industry. Second, the estimated shadow costs are incorporated with the observed market costs and used within a programming framework to calibrate empirical non-linear multi-crop, multi-input production functions. Minimum data requirements of the modelling procedure are described. The calibration procedure is illustrated with a synthetic data set consisting of five crops and three inputs. A framework for evaluating the link between agricultural activities and natural resource depletion is laid out and natural resource depletion rates are computed for five common environmental and resource problems. A numeric illustration is used to estimate the welfare effects from a variety of agricultural policies.
Increasing agricultural productivity has long been a part of national goals to combat hunger, meet subsistence needs, reduce dependence on imports for food and fibre, improve the balance of trade, increase national security and achieve sustainable growth. Griliches (1987) defined productivity as "...a ratio of some measure of output to some index of input use." Growth in agricultural output can be attained through expansion in farmed area, intensification of production and improvement in input use efficiency. However, full consideration of the effect of agriculture on the local environment is important since short-run gains to agricultural productivity can have long-run implications on national output levels. In many countries, agricultural expansion has accelerated depletion of natural resource stocks, deteriorated environmental quality and encroached on sensitive ecosystem habitats. Examining the full effects of agricultural expansion policies on national welfare necessitates productivity analysis of broader scope.
At the onset, researchers hypothesized that expansion of capital and labour could explain the bulk of productivity growth. Studies employing growth accounting methods were able to explain about ten to 15 percent of growth with physical capital formation (Cornwall, 1987; Denison, 1967 and 1987). Bosworth (1982) similarly found little evidence linking the decline in productivity in the 1970s to reduced capital formation during that decade. The residual, approximately 85 to 90 percent unexplained growth, has been broadly interpreted as efficiency gains, technological progress, improved economies of scale and a "measure of our ignorance" (Cornwall, 1987). A better explanation of the large residual may be the reliance on partial analysis in the 1950s, 1960s and 1970s where capital formation was narrowly defined and important input factors were left out of the analysis. Omission of relevant input factors can lead to biased and unreliable results.
Subsequent studies have attempted a more complete analysis through inclusion of physical inputs such as fertilizer and pesticides. Other researchers included labour inputs in their analyses, specifically human capital formation to explain growth (Antholt, 1994; Beal, 1978; Evenson and McKinsey, 1991; Jamison and Lau, 1982; Nehru and Dhareshwar, 1994; Pardey, Roseboom and Craig, 1992; Pray and Evenson, 1991; Rosegrant and Evenson, 1992). Griliches (1963) incorporated the quality of labour in his study on agricultural production in the United States. He used education as a measure of labour quality and included research and extension expenditures to explain growth in productivity. In this fashion, Griliches was able to explain virtually all "unexplained growth" with economies of scale, changes in labour quality and investment in research and development. Support for this work can be found in Abramovitz (1956), Kendrick (1973) and Solow (1957). These authors show that input quality (increased efficiency of input use) rather than quantity can account for three-quarters of the early post-war growth in the United States economy (Metcalfe, 1987). In recent work by Auraujo, Chambas and Foirry (1997), Lachaal (1994), Lin (1992), McMillan, Whalley and Zhu (1989) and Wiens (1983), public policy reforms were investigated to explain productivity growth.
Agricultural productivity loss resulting from environmental degradation has been well documented. Wolman (1985), for example, reports significant losses due to soil erosion of up to 40 percent in the former USSR, 25 percent in the United States, 30 percent in Haiti and 25 percent in Nigeria. In the growth model literature, however, the effects of environmental degradation are conspicuously absent. Part of the omission may be explained by lack of necessary data. Agronomic information on land quality, for example, is not routinely collected and reported with other information on land use. It is also interesting to note that natural habitats are often classified as "unimproved land" and assigned an economic value of zero (FAO, 1996). This is despite the fact that in their "unimproved" state, many lands provide a net positive flow of economic goods and services.
To address the gap in the literature, this paper develops a link between agricultural activity and natural resource stocks to demonstrate a method for including the welfare effects of resource stock depletion in agricultural productivity and policy analyses.
Methods for assessing contribution to productivity growth have included the following: index numbers or growth accounting techniques (Antle and Capalbo, 1988; Diewert, 1976), econometric techniques (Capalbo and Vo, 1988) and mathematical programming procedures (Chavas and Cox, 1992). The drawbacks of these methods are as follows. Growth accounting imposes strong assumptions about the technology, while econometric approaches are data intensive. Both accounting and econometric methods require that the data be aggregated. Mathematical programming methods, while relatively less restrictive, are not statistical and therefore preclude hypothesis testing and construction of confidence intervals.
The premise of this work is an empirical procedure for calibrating flexible agricultural production models which can be used to evaluate the effect of agricultural policy on agricultural productivity, agricultural sector activity, agricultural returns and natural resources.
Agricultural production functions are typically estimated with regression techniques. For some applications, however, the available data are too sparse to parameterize the functions needed to address the problems at hand. For example, an annual data series may report labour, land use and income, but not irrigation water use, capital investment and variable costs. The lack of a corresponding data series prohibits econometric estimation.
When available production data are too sparse for standard regression techniques, functions can be parameterized using calibration procedures. Traditional calibration approaches have relied on constraints to replicate base year observations. The problem is that ad hoc constraints can inadvertently restrict the range of plausible alternatives, thereby limiting the model's uses as a policy tool.
Recent use of calibration methods for economic modelling includes Zhuang (1996) who applied a calibration procedure to estimate a computable general equilibrium model (CGE) of the Chinese economy. He first calibrated the CGE to a base year then modified the model with econometrically estimated behavioural equations to capture the 1983 economy, a year not in competitive equilibrium. Deviations of the base from the equilibrium were attributed to the distorting influence of many years under a command economy.
Pavilos and Yip (1997) examined the case of a small open economy exposed to free trade. They modelled the economy with a dynamic generalized cash advance system and used calibration methods to determine the value of a tariff on imported consumer goods.
A good description of calibration methods can be found in Kydland and Prescott (1982). The reader is also referred to Gregory and Smith (1989) and Kim and Pagan (1993) for excellent reviews of the literature.
The agricultural sector produces a variety of crops and allocates scarce resource inputs to those crops. Except for some rigidity in input and output markets, it can be assumed that production decisions are made jointly and in response to market signals. Market signals are reflected in the prices of agricultural products and the costs of production inputs. Due to heterogeneity in quality of resource inputs, access to resources and access to output markets it is expected to observe a variety of crops produced. The dispersion of values is concealed when the data are highly aggregated, which is found to be the case when working with macro-level data. Models parameterized with aggregate data may not accurately reflect or explain observed cropping patterns and agricultural activities using a strict, profit maximizing, production framework.
A programming model parameterized with observed input use rates, cropping mix and output levels may suggest that at current prices and costs, agricultural profits will be maximized when only the most profitable crops are grown (in contrast to what is observed in practice). To reproduce observed activity, previous researchers have imposed the following restrictive assumptions:
The method described in this paper postulates that because the available market information is aggregated and incomplete, reported price and cost data do not comprise a complete picture of the economic signals that the agricultural sector faces. The approach presented here retains profit maximization as the primary objective, assumes farm production is efficient and employs a set of less restrictive and theoretically more plausible constraints to parameterize production functions.
If agricultural resource inputs were being allocated efficiently, one would expect to observe the following efficiency criteria. The value marginal product of each crop equals the marginal cost of inputs at observed output levels. In reality, this widely accepted economic condition of profit maximization is rarely observed. An empirical explanation is that the marginal cost of resource use includes the observed market cost plus some additional costs, i.e. costs faced by producers that do not appear in economic data series. The first step of the calibration procedure is aimed at estimating these additional or "shadow" costs. To this end, linear programming methods are used to derive the shadow cost of resource use under the following five assumptions.
The shadow cost is defined to be an additional cost to agricultural producers of using resource inputs not reported in economic data series. Through observation of agricultural sector activity (i.e. choice of resource inputs and selection of output levels) under observed market prices and input costs, the true marginal cost of inputs used in production can be determined and thereby the shadow cost can be imputed.
Following Lee and Howitt (1996), for each resource input j = 1,..., J, the shadow cost 8j is defined to be the marginal profitability of the input in the lowest valued crop i = 1,..., I. In equation 3.1, pi is crop price, Qi is total production of crop i, Xij is input quantity, rj is input cost and aij is the linear rate of input use.
 (3.1)
(3.1)
Equation 3.1 can also be expressed as,
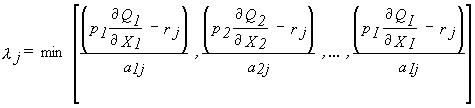 (3.2)
(3.2)
Following equation 3.2, the shadow cost for the jth limiting resource input can be computed.
Using the shadow costs derived in Step 1 and observed market output prices, input costs, the non-linear production function parameters are calibrated. To assure that the calibrated production functions replicate an efficiently operating agricultural sector the following efficiency constraints are specified:
Let crop output levels be represented by Q and be non-linear in input use X. For I crops and J inputs, Q is ( I x 1) and X is (I x J). The production function parameters are given by a which is ( I x (J+1)).
Q = Q ( 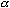 , X) (3.3a)
, X) (3.3a)
The observed output and input levels Q0 and X0 are given. The matrix of parameters 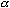 is to be calibrated. The first order condition for profit maximization is given by equation 3.4a implying that production efficiency exists when value marginal product equals marginal input cost. In equation 3.4a, p is an ( I x 1) vector of output prices and marginal input cost is given by r (J x 1) plus the shadow cost
is to be calibrated. The first order condition for profit maximization is given by equation 3.4a implying that production efficiency exists when value marginal product equals marginal input cost. In equation 3.4a, p is an ( I x 1) vector of output prices and marginal input cost is given by r (J x 1) plus the shadow cost 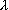 (J x 1).
(J x 1).
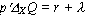 (3.4a)
(3.4a)
The second-order condition for profit maximization, concavity, can be fulfilled by equation 3.5a,
 (3.5a)
(3.5a)
Equation 3.6a assures that the calibrated production model 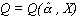 reproduces observed output levels Q0 at the base level of resource allocation X0.
reproduces observed output levels Q0 at the base level of resource allocation X0.
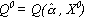 (3.6a)
(3.6a)
Equation 3.7a imposes constant returns to scale on the lowest valued crop in the region.
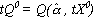 (3.7a)
(3.7a)
Equation 3.8a equates the shadow value of the limiting input with the difference between average and marginal yield for each crop.
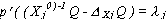 for the limiting resource Xj = XL (3.8a)
for the limiting resource Xj = XL (3.8a)
If noise exists in the data observations from faulty collection procedures, aggregation in the reported data, or another source, then the calibrated model is unlikely to fit the data exactly. To allow for noise in the data, equations 3.4a through 3.8a are appended with an error term  to yield equations 3.4b through 3.8b. The production model parameters,
to yield equations 3.4b through 3.8b. The production model parameters, 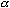 , are calibrated by minimizing the sum of the squared error terms as follows.
, are calibrated by minimizing the sum of the squared error terms as follows.
Choose 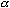 to minimize
to minimize
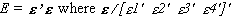 (3.9)
(3.9)
Subject to:
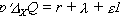 (3.4b)
(3.4b)
 (3.5b)
(3.5b)
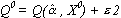 (3.6b)
(3.6b)
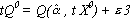 (3.7b)
(3.7b)
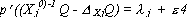 for Xj = XL the limiting resource (3.8b)
for Xj = XL the limiting resource (3.8b)
The methodology described here was developed for use with extremely parsimonious data (single observations). If the method is applied to larger data sets, the results will approximate those of restricted least squares. In general, however, when multiple observations of all model variables are available, the preferred method of estimation is least squares for attaining unbiased, efficient results, properties that are not guaranteed with calibration.
The calibration method described here can be used to evaluate aggregated national data. If disaggregated regional data are also accessible, calibration of regional production functions is recommended. The regional results can then be aggregated to assess the national effects of policy. In this way, analytic results will be more precise. Furthermore, regional results allow for interesting cross-regional comparisons and policy trade-offs.
The minimum data requirements are as follows: total annual crop production; average crop price; land use by crop; total land available for farming; average annual land cost by crop; annualized capital investment; cost of capital; rate of use for other inputs; and per unit cost of other inputs. Observations are needed for at least two crops.
Total annual production of each crop (or average yield per acre2) for the relevant crops grown in the country is needed in addition to the corresponding average wholesale or farm-gate price received for each crop.
Data on land, capital and other inputs are needed for this analysis. Land data requirements include: the total area of land farmed in each crop; the average annual per unit cost of land; and the total amount of land available for farming. If land is the limiting input, then the total available land for farming may be assumed equal to the sum of land in all crops.
Required data on capital include: the total annualized investment in capital for each crop; the cost of capital; and total capital available. If capital is a limiting input, then total available capital for farming may be assumed equal to the total capital investment in all crops.
Other input data required may include the quantity and or quality of additional dominant inputs and their average per unit cost. Since a large number of different inputs are used in farming, it is critical that data are obtained on all inputs subject to change and they may vary by crop type. An analysis of irrigated crops, for example, should include water application rate and water cost. For dryland crops, labour use, pesticide use or fertilizer application rate may take precedent.
The calibration procedure can be applied using exclusively land and capital as inputs. However, the results will not be reliable if another important input is left out. Consider, for example, an evaluation of the effects of a policy restriction. If an important input is left out of the analysis, the model results may fail to anticipate input substitution as an adaptive response. The on-farm cost of policy will be overestimated and the net welfare effects of the policy may be underestimated.
The calibration procedure is illustrated here for a nation producing five crops A, B, C1, C2 and D using three basic production inputs: land, water and capital. Synthetic data for output levels and rates of input use are displayed in Table 3.1. Synthetic "observed" output prices and input costs are shown in Table 3.2.
TABLE 3.1
Observed Output Level and Rate of Input Use per Crop
Crop |
Output level |
Input use |
||
Land |
Water |
Capital |
||
I |
Qi |
XL |
XW |
XK |
A |
98.32 |
28.5 |
49.87 |
2.85 |
B |
512.5 |
5 |
6.50 |
0.50 |
C1 |
1 084.00 |
8 |
8.80 |
0.80 |
C2 |
122.55 |
5.7 |
11.40 |
0.57 |
D |
38.75 |
0.5 |
0.55 |
0.05 |
TABLE 3.2
Observed Output Price and Input Cost
Crop |
Output price |
Input cost (per unit) |
||
Land |
Water |
Capital |
||
I |
pi |
rL |
rW |
rK |
A |
50.62 |
0.055 |
0.008 |
0.10 |
B |
1.95 |
0.04669 |
0.00891 |
0.10 |
C1 |
2.55 |
0.08635 |
0.01319 |
0.10 |
C2 |
17.21 |
0.091 |
0.01 |
0.10 |
D |
3.22 |
0.06246 |
0.01123 |
0.10 |
The production function is specified as Cobb-Douglas with inputs land (L), water (W) and capital (K):
Qi = 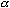 i0 XiL
i0 XiL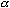 iL XiW
iL XiW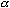 iW XiK
iW XiK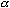 iK, for i = A, B, C1, C2 and D (3.3b)
iK, for i = A, B, C1, C2 and D (3.3b)
The parameterization problem is to find 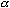 that minimizes the sum of the squared errors (equation 3.9) subject to:
that minimizes the sum of the squared errors (equation 3.9) subject to:
pi 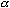 j Qj / Xij = rj +
j Qj / Xij = rj + 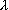 j +
j +  1j for j = L, W, K (3.4c)
1j for j = L, W, K (3.4c)
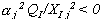 (3.5c)
(3.5c)
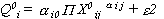 (3.6c)
(3.6c)
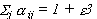 (3.7c)
(3.7c)
pi (Qi / XiL - 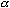 j Qi / XiL ) =
j Qi / XiL ) = 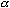 L +
L +  4 (3.8c)
4 (3.8c)
where XL is the limiting resource and for all crops i.
Solving the system of equations given by equations 3.4c through 3.8c and 3.9 parameterized by the information in Tables 3.1 and 3.2 yields the calibrated Cobb-Douglas parameter values in Table 3.3. The calibrated model can be calibrated by comparing empirical output levels at observed input use rates to "observed" output levels. Input use rates from Table 3.1 and parameter values from Table 3.3 are used in equation 3.2b to arrive at estimated output Q M. Validation results are shown in Table 3.4. Note that the predicted output levels Q M are fairly close to observed output levels, Q 0 (from Table 3.1). For this synthetic data set, the model calibrated to within two percent.
TABLE 3.3
Calibrated Production Function Parameter Values
Crop |
Calibrated parameters |
|||
Intercept |
Land |
Water |
Capital |
|
I |
|
|
|
|
A |
3.62 |
0.888 |
0.08 |
0.032 |
B |
145.53 |
0.734 |
0.058 |
0.018 |
C1 |
327.00 |
0.539 |
0.042 |
0.015 |
C2 |
44.40 |
0.516 |
0.054 |
0.027 |
D |
66.30 |
0.651 |
0.05 |
0.014 |
TABLE 3.4
Validation of Calibrated Model: Comparison to Observed Output Levels
Output |
|||
Crop |
Observed |
Calibrated Model Estimate |
Calibration Error |
I |
Q0 |
QM |
|
A |
98.32 |
100.22 |
2 percent |
B |
512.50 |
522.06 |
2 percent |
C1 |
1084.00 |
1095.28 |
1 percent |
C2 |
122.55 |
122.43 |
<1 percent |
D |
38.75 |
39.29 |
1 percent |
The calibrated results from section 3.4 provide sufficient information for estimating marginal product of capital, value marginal product of capital, marginal product of land and value marginal product of land. This section provides estimates of the value of marginal product for each crop. These values can be used to indicate which crops will yield the greatest net gains from capital enhancement policies and which crops will produce the highest net returns with area expansion policies.
To compare returns to capital investment across crops, the marginal product of capital and the value of the marginal product of capital for each crop are computed. The marginal product of capital can give the increase in total crop output that will occur with a small infusion of capital. Multiplying the marginal product of capital by the price received for the crop, the value of the marginal product of capital is obtained, the value of additional output that would be generated by a small increase in capital investment.
The value of the marginal product of capital, VMPK, is estimated using the calibrated slope coefficient on capital 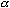 i,K (table 3.3); observed output of crop i, Qi (Table 3.1); capital input level Xi, K (Table 3.1); and the definition of the marginal product of capital, MPK for a Cobb-Douglas production,
i,K (table 3.3); observed output of crop i, Qi (Table 3.1); capital input level Xi, K (Table 3.1); and the definition of the marginal product of capital, MPK for a Cobb-Douglas production,
MPi, k = 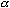 i, k Qi / Xi, k (3.10)
i, k Qi / Xi, k (3.10)
The value of the marginal product of capital is defined by
VMPk = pi MPk (3.11)
where pi is the unit price of crop i (Table 3.2).
As shown in Table 3.5, the marginal product of capital for crop C1 is 20.32, the largest in the group. At the margin, a one unit increase in capital investment in crop C1 will result in a 20.32 unit increase in output of crop C1. By comparison, increasing the quantity of capital used in the production of crop A generates a 1.10 unit increase in output. In terms of units of output, crop C1 is the better investment. Comparing output units of different crops, however, is like comparing apples and oranges. To denominate crop outputs in comparable units, each crop's marginal product is multiplied by its own price and in this way the additional (marginal) revenue generated with a unit increase in capital investment can be evaluated.
TABLE 3.5
Marginal Product of Capital and Value of the Marginal Product of Capital
at "Observed" Output Levels and Rate of Input Use
Crop |
Marginal Product of Capital |
Value of the Marginal Product of Capital |
| I | MPi,K |
VMPI,K |
A |
1.10 |
$55.88 |
B |
18.45 |
$35.97 |
C1 |
20.32 |
$51.82 |
C2 |
5.80 |
$99.90 |
D |
10.85 |
$34.93 |
TABLE 3.6
Marginal Product of Land and Value of the Marginal Product of Land
at "Observed" Output Levels and Rate of Input Use
Crop |
Marginal Product of Land |
Value of the Marginal Product of Land |
I |
MPL |
VMPL |
A |
3.06 |
$155.07 |
B |
4.57 |
$8.91 |
C1 |
5.17 |
$13.19 |
C2 |
0.58 |
$9.99 |
D |
3.52 |
$11.34 |
Results indicate that a unit increase in capital investment in crop C2 will generate, at the margin, US$99.90 in revenues. It is important to note that the Cobb-Douglas specification assures that output is non-decreasing in input use. Furthermore, the output market is assumed to be perfectly competitive, that is, producers can sell as much as they produce without influencing the price. Therefore, within the model context value of the marginal product, VMP, is non-decreasing in all non-binding inputs and furthermore the "observed" level of capital is assumed to maximize production profits. In this illustration, capital is a non-binding resource, so any increase in capital above the observed level of use will lower net returns to agriculture.
In some countries, however, capital is the binding resource. Therefore, actions that increase the availability of capital to the agricultural sector through external investment, subsidization, guaranteed loans and technological innovations, would lead to an increase in net returns to agriculture.
Results show that from an additional unit of land, crop C1 returns the greatest increase in total output as indicated by the computed marginal product of land for crop C1 of 5.1736. The crop with the smallest gain with an increase in land was C2 with a marginal product of land equal to 0.5805. The value of the marginal product of land or VMPL, as shown in Table 3.6 is greatest for crop A. A unit increase in arable land will raise revenues by $155.08. By comparison, a unit increase in land planted in crop B will yield an increase of $8.92.
Agricultural expansion encroaches on forested area, wetland habitats and desert communities. Once habitat is lost, tilling and irrigation of the land depletes soil nutrients and erodes topsoil. Supplemental nutrients can be introduced to enhance soil productivity, but excess nutrients can leach through the soil, contaminate underground aquifers and erode the quality of surface water systems.
For many years, the loss in natural resource amenities was accepted as a reasonable tradeoff to meet national needs for food, fibre and export products. Increased scarcity of natural resource stocks and greater awareness of the services provided by intact natural resources suggests that a more complete accounting of the welfare effects from resource stock depletion be considered in agricultural policy analysis. This section develops simple linking equations between agricultural activity and resource stock depletion, then uses those equations to evaluate the economic welfare effects of diminished stocks.
National income accounting methods can be used to illustrate in a stylized manner the relationships among agricultural activities, natural resource stock depletion and social welfare. Borrowing notation from Dasgupta and Heal (1979) S measures the resource stock and S denotes the partial derivative of the stock with respect to time, that is, the change in the resource stock over time.
Depletion of the resource stock is indicated by: 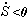
and regeneration or restoration of the resource stock will occur when: 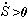
In steady state,  = 0.
= 0.
The natural resource stock is assumed to provide a flow of services either in its intact state or through extraction. Non-timber goods and services from forested lands, for example, include food (nuts, roots, plants), materials (bark, plant fibres, etc.), CO2 absorption, habitat and recreational services. If timber is harvested and not replanted, the forested area decreases and the flow of services diminishes as well. Thus, if the flow of services can be valued, then the loss in the flow of services due to the depletion of the resource stock can also be valued. Using a simple linear form, let v represent the present value of a unit of the resource stock. Then the present value of a change in the resource stock is expressed, v  .
.
Social welfare from agriculture production, W, can be expressed as the utility from consumption of agricultural goods U(C) less the value of the depletion of the resource stock:
v  '
'
W = U(C) + v  (3.12)
(3.12)
In this simple case, assume that the society is closed so the amount available for consumption equals the quantity produced Q.
C = Q (3.13)
The quantity of goods produced Q is a function of inputs into production given by equation 3.3a. Using the production functions developed in the previous section, 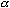 are the production function parameters and X is the matrix of inputs into production, in this case land, water and capital. If the rate of resource stock depletion corresponds with agricultural resource use, the change in the resource stock can be written as,
are the production function parameters and X is the matrix of inputs into production, in this case land, water and capital. If the rate of resource stock depletion corresponds with agricultural resource use, the change in the resource stock can be written as,
 = h (
= h (  , X) (3.14)
, X) (3.14)
Here  is the vector of stock depletion parameters. The following section describes simple functional forms for modelling natural resource stock depletion: groundwater stock depletion, groundwater contamination, deforestation, soil salinization and soil erosion. In the equations that follow, XW represents water use, XF measures fertilizer application, XL indicates land in agriculture and XK denotes investment in resource conserving capital.
is the vector of stock depletion parameters. The following section describes simple functional forms for modelling natural resource stock depletion: groundwater stock depletion, groundwater contamination, deforestation, soil salinization and soil erosion. In the equations that follow, XW represents water use, XF measures fertilizer application, XL indicates land in agriculture and XK denotes investment in resource conserving capital.
Groundwater Depletion
Most of the world's crops are irrigated with groundwater. When the rate at which water is pumped from the groundwater source exceeds the rate of recharge to the source, the stock of groundwater declines. The stock S can be defined as the volume of groundwater available for pumping. The change in the stock, S, can be expressed as a function of the rate of water use XW
 =
=  0 -
0 -  1 XW (3.15)
1 XW (3.15)
Here  0 is the natural recharge rate and
0 is the natural recharge rate and  relates the rate of irrigation water use with aquifer drawdown. For example, in an aquifer with a very slow recharge rate
relates the rate of irrigation water use with aquifer drawdown. For example, in an aquifer with a very slow recharge rate 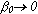 . In an aquifer with little or no return flow
. In an aquifer with little or no return flow 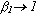 .
.
Groundwater Quality Contamination
Chemical and nutrient inputs to agricultural crops can leach through the soil and contaminate groundwater supplies. Following Kim, Sandretto and Lee (1999), groundwater contamination, from fertilizer application XF and irrigation water XW, can be expressed as follows where S is the stock of fertilizer in the groundwater:
 = h (XF, XW, S ) (3.16)
= h (XF, XW, S ) (3.16)
Deforestation
Agricultural area expansion often occurs on cleared forestlands. Timber is harvested and then cleared for agriculture. Following Garcia (1998), where S is forested area, agricultural encroachment on forestland can be expressed as,
 = -
= - 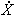 L (3.17)
L (3.17)
Soil Salinity
Irrigation water can leach salts from the soil into drainage water. If drainage water is returned to the water supply system, over time the water and the soils can become more and more saline (Lee and Howitt, 1996). If S measures water quality, then a simple function can be written indicating that water quality is decreasing (becoming more saline) in water application, XW and increasing in improved irrigation technology, XK.
 =
=  2 XW +
2 XW +  3XK (3.18)
3XK (3.18)
Soil Erosion
Agricultural activities can erode top soil and deposit sediment in the waterways. After many years, the soil base can become depleted, crop yields decline and production becomes unprofitable. Typically, tillage and irrigation practices contribute to the rate of soil erosion. Where S is the stock of soil, soil erosion can be expressed as increasing in water use XW and decreasing in investment in soil conserving capital XK.
 = -
= -  4 XW +
4 XW +  5XK (3.19)
5XK (3.19)
The following example illustrates the welfare effects of depleting a resource stock, groundwater. Suppose irrigation water is being pumped from a slowly recharging aquifer. The rate of stock depletion is given by equation 3.15. Consider this simplest case. The recharge rate is very slow,  0 = 1.0 and the discharge rate is equal to three-fourths the pumping rate,
0 = 1.0 and the discharge rate is equal to three-fourths the pumping rate,  1 = 0.75.
1 = 0.75.
Then,  = 1.0 X 0.75 XW.
= 1.0 X 0.75 XW.
The social value of water in the aquifer is set equal to US$1.10 as shown in Table 3.8. Multiplying v by the annual change in stock, gives the value of stock depletion, v  (Tables 3.8 and 3.9).
(Tables 3.8 and 3.9).
TABLE 3.7
Economic Returns to Agriculture
Crop |
Revenue |
Cost |
Profit |
Profit per Acre |
TR |
TC |
B |
B/XL |
|
A |
$4977.21 |
$2127.29 |
$2849.91 |
$99.99 |
B |
$999.37 |
$309.16 |
$690.21 |
$138.04 |
C1 |
$2764.20 |
$847.74 |
$1916.45 |
$239.55 |
C2 |
$2109.08 |
$689.48 |
$1419.59 |
$249.05 |
D |
$124.77 |
$39.10 |
$85.66 |
$171.33 |
Total |
$6961.82 |
Table 3.8
Natural Resource Stock Depletion (Groundwater)
Crop |
Stock unit value |
Change in Stock |
Value of Stock Depletion |
V |
S |
vS |
|
A |
$1.10 |
-36.4063 |
-$40.05 |
B |
$1.10 |
-3.875 |
-$4.26 |
C1 |
$1.10 |
-5.6 |
-$6.16 |
C2 |
$1.10 |
-7.55 |
-$8.31 |
D |
$1.10 |
0.5875 |
$0.65 |
TABLE 3.9
Natural Resource Stock Depletion and Net Welfare
Crop |
Profit |
Value of Stock Depletion |
Net Welfare |
|
B/XL |
v S |
W |
A |
$100.00 |
-$40.05 |
$59.95 |
B |
$138.04 |
-$4.26 |
$133.78 |
C1 |
$239.56 |
-$6.16 |
$233.40 |
C2 |
$249.05 |
-$8.31 |
$240.75 |
D |
$171.33 |
$0.65 |
$171.98 |
Total |
$897.98 |
-$58.13 |
$839.85 |
This illustration shows how to approximate the cost of an environmental externality arising from an agricultural activity. Results show that crop C2 yields the highest net welfare per acre (US$240.75) even when the externality is accounted for (Table 3.9). Crop A generates the largest external cost per acre (US$40.05). Production of crop D has a small beneficial impact on the environ-ment, US$0.65 per acre, resulting from a water withdrawal rate that is lower than the recharge rate.
This paper presented an empirical approach for evaluating agricultural production and analysing the economics of agriculturally induced resource externalities. The two-step calibration procedure presented here can be used to parameterize multi-crop, multi-input production models that closely reproduce observed input and output levels under observed market conditions in a relatively unconstrained setting. The parameterized model follows first order and second order conditions for profit maximization at observed output levels. An illustration with five crops and a Cobb-Douglas model specification in land, water and capital was used to demonstrate the procedure.
Empirical results were used to compute the value of the marginal product of capital to show how investment in capital accumulation can increase agricultural sector returns. A comparison of the computed value of the marginal product of capital between crops indicated which crops yield the greatest return to investment. Model results were also used to compute the value of the marginal product of land to reveal the marginal returns to area expansion. Comparing the value of the marginal product of land between crops reveals the crops that would contribute the greatest returns to the agricultural sector from additional area.
Simple linking equations between agricultural activities and natural stocks were proffered for groundwater overdraft, groundwater contamination, deforestation, soil salinization and soil erosion. The linking equations were parameterized and then used to demonstrate how to account for the social welfare effects of resource degradation from agricultural enhancement policies.
A logical extension of this work is an application of the calibration procedure to country level agricultural data and specification and parameterization of one or more of the linking resource depletion equations. Another interesting area of follow-up work is a side-by-side comparison of estimation results from the calibration methodology and econometric methodology.
Abramovitz, M. 1956. Resource and output trends in the United States since 1870. American Economic Review, Papers and Proceedings, 46 (May): 5-23.
Antholt, C.H. 1994. Getting ready for the twenty-first century: technical change and institutional modernization in agriculture. World Bank Technical Paper #217, February. Washington. DC. World Bank.
Antle, J. & Capalbo, S. 1988. An introduction to recent developments in production theory and productivity measurement. In S. Capalbo & J. Antle, eds. Agricultural productivity measurement and explanation. Washington, DC, Resources for the Future.
Auraujo, B., Chambas, C.G. & Foirry, J.P. 1997. Consequences de l'ajustement des finances publiques sur l'agriculture marocaine et tunisienne, unpublished FAO study, March.
Beal, D.W. 1978. Agricultural education and training in developing countries. FAO studies in Agricultural Economics and Statistics, 1952-1977. Rome, FAO.
Bosworth, B. 1982. Capital formation and economic policy. Brookings Papers on Economic Activity, 2: 273-317.
Capalbo, S. & Vo, T. 1988. A review of evidence on agricultural productivity and aggregate technology. In S. Capalbo & J. Antle, eds. Agricultural productivity measurement and explanation. Washington, DC, Resources for the Future.
Chavas, J.P. & Cox, T. 1992. A nonparametric analysis of the influence of research on agricultural productivity. American Journal of Agricultural Economics, 74: 583-591.
Cornwall, J. 1987. Total factor productivity. In J. Eatwell, M. Milgate & P. Newman, eds. The new Palgrave dictionary of economics, vol 4. New York, USA, Stockson Press.
Dasgupta, P.S. & Heal, G.M. 1979. Economic theory and exhaustible resources. Cambridge, UK, Cambridge University Press.
Denison, E. 1987. Growth accounting. In J. Eatwell, M. Milgate & P. Newman, eds. The new Palgrave dictionary of economics, vol 2. New York, USA, Stockson Press.
Denison, E. 1967. Why growth rates differ: postwar experience in nine Western countries. Washington, DC, Brookings.
Diewert, W.E. 1976. Exact and superlative index numbers. Journal of Econometrics, 4: 115-145.
Evenson, R.E. & McKinsey, Jr., J.W. 1991. Research, extension, infrastructure, and productivity change in Indian agriculture. In R.E. Evenson and C.E. Pray, eds. Research and productivity in Asian agriculture, p. 158-184. Ithaca, USA, Cornell University Press.
FAO. 1996. A system of economic accounts for food and agriculture. FAO Statistical Development Series 8. Rome, FAO.
Garcia, M.C. 1998. Public forest resource management in a developing country: a study of deforestation in the Philippines. Ph.D. Dissertation, Department of Agricultural and Resource Economics, University of Hawaii, Honolulu, USA.
Gregory, A. & Smith, G. 1989. Calibration as estimation. Econometric Reviews, 9:57-89.
Griliches, Z. 1963. The sources of measured productivity growth: United States agriculture 1940-1960. Journal of Political Economics, 71: 331-346.
Griliches, Z. 1987. Productivity: measurement problems. In J. Eatwell, M. Milgate & P. Newman, eds. The new Palgrave dictionary of economics, vol 3. New York, USA, Stockson Press.
Jamison, D. & Lau, L. 1982. Farmer education and farm efficiency. Washington, DC, World Bank.
Kendrick, J. 1973. Postwar productivity trends in the United States, 1948-1969. New York, USA, National Bureau of Economic Research.
Kim, C.S., Sandretto, C. & Lee, D.J. 1999. Controlling groundwater quality with endogenous regulatory instruments. Natural Resource Modeling, 12 (2):249-272.
Kim, K. & Pagan, A. 1993. The econometric analysis of calibrated macroeconomic models. In H. Pesaran & M. Wickens, eds. Handbook of Applied Econometrics, Vol. 1. London, Blackwell Press.
Kydland, F. & Prescott, E. 1982. Time to build and aggregate fluctuations. Econometrics, 50:1345-70.
Lachaal, L. 1994. Subsidies, endogenous technical efficiency and the measurement of production growth. Journal of Agriculture and Applied Economics, 26 (July): 299-310.
Lee, D.J. & Howitt, R.E. 1996. Modeling regional agricultural production and salinity control alternatives for water quality policy analysis. American Journal of Agricultural Economics, 78: 41-53.
Lin, J.Y. 1992. Rural reforms and agricultural growth in China. The American Economic Review, 82 (March):34-51.
McMillan, J., Whalley, J. & Zhu, L. 1989. The impact of China's economic reforms on agricultural productivity growth. Journal of Political Economy, 97 (August):781-807.
Metcalfe, S. 1987. Technical change. In J. Eatwell, M. Milgate & P. Newman, eds. The new Palgrave dictionary of economics, vol 4. New York, USA, Stockson Press.
Nehru, V. & Dhareshwar, A. 1994. New estimates of total factor productivity growth for developing and industrial countries. World Bank Policy Research Working Paper #1313, June.
Pardey, P.G., Roseboom, J. & Craig, B.J. 1992. A yardstick for international comparisons: an application to national agricultural research expenditures. Economic Development and Cultural Change, 40: 333-349.
Pavilos, T. & Yip, C.K. 1997. The gains from trade for a monetary economy once again. Canadian Journal of Economics, 1: 208-223.
Pray, C.E. & Evenson, R.E. 1991. Research effectiveness and the support base for national and international agricultural research and extension programs. In R.E. Evenson and C.E. Pray, eds. Research and Productivity in Asian Agriculture. Ithaca, USA Cornell University Press.
Rosegrant, M.W. & Evenson, R.E. 1992. Agricultural productivity and sources of growth in South Asia. American Journal of Agricultural Economics, 74 (August): 757-761.
Solow, R. 1957. Technical change and the aggregate production function. Review of Economics and Statistics, 39 (August): 312-320.
Wiens, T.B. 1983. Price adjustment, the responsibility system, and agricultural productivity. American Economic Review, 73 (May):319-324.
Wolman, M.G. 1985. Soil erosion and crop productivity: a worldwide perspective. In R.F. Follett & B.A. Stewart, eds. Soil erosion and crop productivity. Madison, Wisconsin,USA, American Society of Agronomy.
Zhuang, J. 1996. Estimating distortions in the Chinese economy: a general equilibrium approach. Economica, 3 (252):543-69.
1 These are strong assumptions that may not apply to all nations. If input and output markets are not perfectly competitive, or externalities exist between regions, a weaker assumption can be substituted without much loss. This may be done by assuming that a managing entity (e.g. the national government) regulates agricultural production and agricultural markets (through taxes, subsidies, quotas and mandates, for example), thereby fully internalizing the social cost of externalities and achieving efficiency within the agricultural sector. Externalities to other sectors may still exist.
2 1 acre = 0.4 ha (approx.).