The epidemiology of a disease is traditionally analysed in time and space. The GIS-based analyses have provided an excellent basis for looking at spatial variables. They have also added a time dimension where they have looked at probable changes in the relevant livestock and human populations over time (e.g. Reid et al., 1999; Gilbert et al., 2001; Hendrickx, 2001). The discussion on methodology above showed how important the time frame is when comparing “with” and “without” project scenarios. Thus, from the economic point of view, there needs to be a parallel understanding of how the benefits and costs of controlling the disease evolve over time with changing human and livestock populations.
Tsetse control
The wide range of currently available techniques for controlling tsetse will be known to most readers. Table 3 lists a selection of cost estimates made in the last decade. The most detailed study of comparable costs using different techniques was that done by Barrett (1997) based on costs in Zimbabwe and, to a lesser extent, Zambia. These have been updated to current prices by Budd (1999) and are summarized in Table 3. Figures per linear kilometre of barrier are also taken from Budd (1999). These provide an idea of the “hierarchy” of costs that might be expected - although their relative costs do, like everything else relating to tsetse and trypanosomiasis, vary from situation to situation. Recent experience in Botswana indicated that aerial spraying costs may be somewhat lower than in the estimates for Zimbabwe, with costs under US$300 per km2, for insecticide and flying time alone (R. Allsopp, personal communication). Estimates for SIT costs range from US$250 to US$800 per km2, depending very much on scale and local conditions (U. Feldmann, personal communication). In West Africa, an annual cost for tsetse suppression using mono-pyramidal traps at low density was US$26 (Shaw, 1993). This low figure reflects both the use of very cost-effective technology and the fact that the goal was suppression, so that traps were not serviced during the rainy season. In addition these costs are very realistic, since they include virtually all in-country overheads such as bank charges, expatriate salaries, depreciation, ongoing research and surveillance activities. This programme planned to gradually involve farmers in cost sharing and responsibility for tsetse control, with mixed results (Krüger et al., 2001). The cost of pour-ons currently ranges from around US$0.60 to US$1.50 per adult cattle dose, with prices varying from location to location, depending on the product and on whether they are sold directly to farmers or purchased in bulk by an organization. More importantly, from the cost point of view, the frequency with which cattle need to be dosed, and the number of cattle which need to be treated per km2 varies greatly as well. The benefit - cost analysis undertaken on the pour-on trial in Ethiopia by Woudyalew et al., (1999) came up with a figure of US$60 per km2 at 1996 price levels. Lastly, as readers will know, trypanocide prices currently also range between US$0.75 and US$2.00 a dose, depending on the type of drug and the cost of delivery.
TABLE 3
Estimated costs of tsetse eradication or
control
|
Technique |
Costs per km2 (US$) |
Objective and location |
|
|
Ground spraying 1, 2 |
265-315 |
Eradication, Zimbabwe and Zambia, flat terrain. |
|
|
Aerial spraying1, 2 (SAT) |
345-535 |
|
|
|
Cattle treatment 1, 2 (pour-on, 15 cattle per km2) |
50-120 |
|
|
|
Linear km of barrier using targets1 |
|
Barrier, general, based on Zimbabwe and Zambia. |
|
|
|
· barrier establishment |
2 000 |
|
|
|
· annual barrier maintenance |
1 600 |
|
|
Aerial spraying3 (SAT) |
265-275 |
Eradication, Botswana. |
|
|
Sterile insect technique4 (SIT) |
800 |
Eradication, Eastern Africa. |
|
|
|
250-400 |
Eradication, Western Africa. |
|
|
Low-density mono-pyramidal traps5 |
26 |
Annual cost of control, Côte d’Ivoire. |
|
|
Cattle treatment6 (pour-on, 44 cattle per km2) |
60 |
Annual cost of control, Ethiopia. |
|
Sources:
The comparative figures given in Table 3 thus provide an initial insight into what the relative costs of the different tsetse control techniques might be. But, when interpreting these figures, it is necessary to realize that the table is not comparing like with like; to a lesser extent, however, than the comparison of “apples and oranges”, discussed in McDermott and Coleman (2001) when modelling the effects of tsetse control, trypanocide use and the potential impact of a vaccine. However, in Table 3, once-off “eradication” approaches are listed alongside annual expenditures on control. An effective comparison of these would involve using the approach described in Chapter 3, “Time value of money”, page 11, discounting all costs incurred over an appropriate time period to their present value and then weighting them by the relative effectiveness of each approach in reducing the impact of the disease.
Next, when comparing these figures, it is important to be very clear about what is included and what is excluded from these cost estimates. Figure 3 illustrates the range of components that go to make up the full cost of tsetse control. This list may not be complete for every technique. However, it attempts to show a graduated list of cost items, ranging from those at the top - the variable, direct, field costs; to those at the bottom - the indirect, fixed costs. The items in the dark area at the top are nearly always included in costings of tsetse control, then moving down the list into the lighter area, the items listed are more and more likely to be omitted from cost estimates.
FIGURE 3
Categories of tsetse control costs - included
or excluded?

There are sound reasons for this. There has been a long tradition of including only what are called “field” or “direct” or “operational” costs when reporting costs of tsetse control per km2. In economics these would mostly be categorized as variable costs and refer to the extra costs involved in mounting a particular control operation. These always cover the costs of insecticide, traps, targets and most of the aeroplane hire costs. Sometimes the costs of travel allowances for staff, field staff salaries and vehicle running are included. The salaries of senior staff, expatriates, of running a headquarters and of supervising the project are seldom included. Further down the list in Figure 3, mapping, monitoring and research, although costed independently are usually excluded from the per km2 cost estimates. The reason for this is that the costs per km2 were mainly worked out by scientists studying which of the various techniques being developed performed best in the field. The work was usually undertaken with an established tsetse control unit in the background. The existence of overheads was always acknowledged, but their relevance to field-level analyses of cost effectiveness was thought to be limited. Such costings were never designed to be used as a basis for planning large-scale operations in the absence of an existing tsetse control infrastructure.
Barrett (1997) is very clear about what has and has not been included in his costings:
direct costs are for “primary field activity” and cover chemicals, human resources and equipment employed in the field, and relate directly to the costs of an operation;
indirect costs “arise in secondary field activities” and cover camp and access provision, aerial spraying contractors’ fixed charges, etc.;
overhead costs consist of a share of the costs of running the tsetse and trypanosomiasis control programme (management, administration, training, surveys, research).
The figures on which the Zimbabwe and Zambia estimates in Table 3 are based include the direct and indirect costs but not overheads. Barrett thus explains that this makes it possible to compare different tsetse control strategies, but states that overheads would have to be included in order to compare tsetse control costs to controlling the disease using trypanocidal drugs. Doran (2000) gives costs for tsetse control and veterinary services in some RTTCP countries.
To look at the significance of overheads for a well-documented West African example of tsetse eradication, in the course of their evaluation of the work in Nigeria, Putt et al. (1980) undertook a detailed analysis of the actual recorded costs of 65 spraying operations. In this analysis the field costs consisted of insecticide, labour, the direct costs of staff involved in the operation (allowances and their salaries during the spraying period), vehicle running, depreciation of equipment and helicopter flying time. A number of helpful conclusions can be drawn from the analysis.
At the field level costs for ground spraying appeared much cheaper than helicopter spraying, this is partly because the helicopter flying charge already included quite a few fixed cost components, such as depreciation on helicopters (Barrett succeeded in adjusting for this in his analyses).
Once all the overheads have been added, helicopter spraying appeared somewhat more expensive, but the difference had narrowed down a lot.
The real cost per km2 of ground spraying was four times its field cost (this was reduced to about three times, after adjusting to take into account several factors, in particular a dramatic reduction in the amount of work done during the last 2 years studied which increased the share of overheads relative to the low budget allocation for field work).
Thus, it is clear that, as well as the obvious adjustment for West African conditions, most of the eradication estimates presented in Table 3 would need considerable upward revision to include overheads before they could be used as a basis for planning the total costs of a real tsetse clearance operation. Often there are also overheads in the project preparation stage, involving applied research, pilot projects, surveys, etc. For the example of low-density trapping in Côte d’Ivoire, although the calculation per km2 was the most comprehensive of those given in Table 3, this cost would still approximately double if the preliminary pilot adaptive research phase was included. The need to carefully consider overheads is all the greater if:
the local institutional structure for undertaking this work does not exist (equipment is therefore needed for new offices, new field and administrative staff need to be trained, etc.);
an international body is to be created in order to supervise and coordinate this work on an international scale.
There are important lessons to be learned here from analysing real overheads involved in creating and running FITCA and RTTCP as well as those incurred by NGOs involved in this type of project. The potential for the existence of such “dis-economies” of scale due to the creation of international super-structures was discussed and recognized at a recent workshop (FAO and IAEA, 2002). These need to be balanced against the economies of scale discussed in Budd (1999). The need to find ways of avoiding incurring overheads associated with the larger scale, more top-down approaches, has been one of the main reasons for trying to develop farmer-based tsetse control methods over the last few decades.
|
BOX 1
|
FIGURE 4
Relationship between tsetse control costs and
human population density
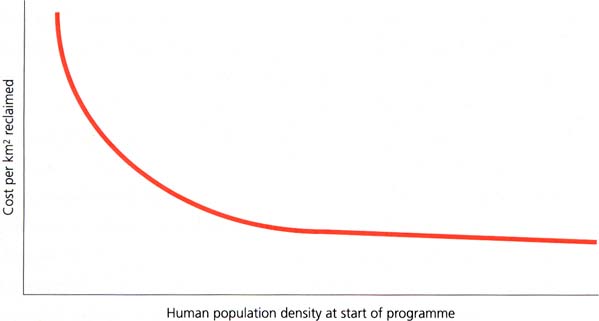
Source: Shaw (1986)
There is thus a twofold requirement:
to update current knowledge on tsetse control costs in the field, and do this for West African situations;
to try to quantify likely levels of overheads associated with the different approaches.
From the discussion above, from established knowledge, and published detailed cost analyses (Barrett, 1997; Brandl, 1988b; Putt et al., 1980) the main factors that influence the costs of tsetse clearance have been summarized in Box 1. Obviously, there is variation according to the technique used, but these factors generally hold true.
In West Africa, it is likely that human population density is a key variable in determining the level of costs. A modelling exercise based on Nigerian data (Shaw, 1986) came up with a relationship such as that illustrated by the curve in Figure 4. The variables included in the GIS analysis (Hendrickx et al. 1997; PAAT, in prep.; Hendrickx, 2001) very much complement and reinforce this relationship and the selection of this parameter as a crucial one.
FIGURE 5
Relationship between trypanocide costs and
cattle population density
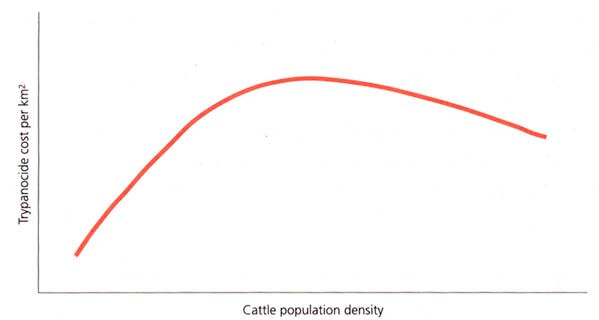
Trypanosomiasis control using drugs in cattle
Aspects of the use of trypanocides have been discussed in Chapter 3, “‘With’ and ‘without’ project scenarios for costs”, page 21. In terms of how these costs behave, it appears that they:
increase linearly with cattle population density (see Figure 1);
increase with tsetse challenge (which tends to be higher at low human population densities).
In general the cattle population will increase as the human population increases, up to the point where cultivation density is such that the population of herd cattle (as against draught animals) that an area can support is reduced. Thus, the cost per km2 of effectively controlling the disease with trypanocides could follow a curve such as that shown in Figure 5. It will increase in line with the cattle population and then could reduce slightly, as fewer doses per head of cattle would be required at high population densities, when tsetse challenge is likely to be lower. However, if drug resistance emerges over time, then the amount of trypanocide needed would increase, changing the shape of the curve, and making it time dependent. Thus, the form taken by the curve is likely to vary according to circumstances and should be modelled with respect to specific situations in order to illustrate the relationship more clearly.
Actual expenditure (as against the amount required to effectively control the disease) would depend on the extent to which cattle keepers use trypanocides, in turn reflecting their incomes, their knowledge of the disease and drug availability. As stated above, finding out about current levels of drug use and assessing what proportion of losses due to the disease are being prevented by the current use of trypanocides are crucial to understanding the economics of controlling the disease.
The issue of drug resistance and its current extent has been much debated, and falls outside the scope of this paper. Doran (2000) comments that the way in which drugs are being used in the RTTCP countries is, according to the guidelines given in Geerts and Holmes (PAAT, 1998), unlikely to cause resistance.
As everyone who has grappled with the issue will be well aware, quantifying and analysing benefits is a far more complex issue than tackling costs. This is due to the need to integrate the following variables in any model of what level of benefits to expect:
tsetse challenge;
human and livestock, especially cattle, populations inside the project area;
human and livestock, especially cattle, populations outside the project area, a measure of land pressure in the surrounding region, and of potential immigration;
breed of cattle likely to be affected;
specific characteristics of the production system, i.e. crops grown, use of draught power and livestock management practices.
Techniques and approaches used in quantifying benefits
A very wide range of techniques has been used for quantifying actual or potential benefits in the economic analyses cited in Chapter 1.
Kristjanson et al. (1999) used an economic surplus model to analyse the potential benefits on a continent-wide scale if a vaccine were developed for trypanosomiasis. They looked at how demand and supply might shift in response to a greater availability of meat and milk (as calculated using a herd model) and at how this would benefit consumers and producers of these products once prices had adjusted in response to the new supply and demand situation.
As mentioned in the initial discussion in Chapter 1, the estimated elasticity[3] for the change in agricultural production with respect to a change in livestock numbers has been used by Swallow (PAAT, 2000) and Budd (1999) to estimate how agriculture would benefit from increased numbers of cattle following removal of tsetse from large areas of the continent. This attempts to capture, on a macroeconomic scale, in addition to the increased output from livestock, the effect of the presence of livestock on crop farming, through greater availability of manure, use of draught animals and a more balanced portfolio of farm enterprises (crops and livestock) for farmers.
Contingent valuation saw, what was probably its first application to tropical animal health issues, through the work of Swallow and Woudyalew (1994) in Ethiopia and was used in West Africa in studies in Burkina Faso (Kamuanga et al., 2001b), Côte d’Ivoire and the Gambia which are all summarized in Kamuanga (PAAT, 2003). This technique, which has been extensively used in human health economics and environmental economics, was developed as an attempt to value goods such as human health or conservation goals by asking individuals affected by the issue what they were “willing to pay” for a specific outcome. In the field of tsetse and trypanosomiasis, a standardized approach has been developed and used to study people’s willingness to contribute labour or money to actual control schemes and to see how their estimates varied over time, and were borne out by the contributions eventually made. The reader should consult PAAT (2003) for a detailed discussion of the issues involved.
The development of GIS has provided a powerful tool for identifying and prioritizing areas for tsetse and trypanosomiasis control (see, among many others, Gilbert et al., 2001; Hendrickx et al., 1999; PAAT, in prep.; Hendrickx, 1999, 2001.) The PAAT information system (PAATIS, see Gilbert et al., 2001) in particular has shown that GIS can focus on most of the issues that are essential in evaluating the economic impact of potential control and eradication schemes. It can highlight potential areas for livestock and crop development, as well as predicting tsetse distribution and identifying areas where the fly is vulnerable to habitat change (e.g. Reid et al., 1999). Indeed, much of what has come out of the GIS work is an answer to the prayers of economists and decision-makers trying to tackle the problem two or three decades ago.
The wide range of PRA and RRA techniques developed over the last 15 years have also contributed towards our understanding of the trypanosomiasis problem and farmers’ and livestock-keepers’ perceptions of how it affects them and how they deal with it. Techniques specific to the tsetse and trypanosomiasis problem have also been developed (Snow and Rawlings, 1999). These have made it possible to assess such situations in a structured way. They have been reinforced by the development of techniques specific to livestock keepers (e.g. IIED, 1994, 2002; Heffernan et al., 2003). The use of surveys and, in particular, recall data whereby farmers are asked to recall livestock events over a defined period, usually the last year, has been very helpful in enabling reasonably accurate information to be gathered at a moderate cost (e.g. Kamuanga et al., 2001a; Doran, 2000). When using these various tools, it is important to be aware of the strengths and weaknesses of different approaches, and of which elicit the best information in various circumstances (see Misturelli and Heffernan, 2003).
Herd models are mathematical simulations of livestock demographics, incorporating different production parameters (such as mortality and fertility rates) so as to simulate different health statuses of the populations, and thus the effects of disease, or of animal health control measures on disease. A wide range of herd models exists. These can be classified in various ways (Putt et al., 1987). They can be stochastic (incorporating values for the various parameters which follow probability distributions) or deterministic (where the variables take their average value). Static models illustrate the herd’s productivity when it has reached its steady state; dynamic models trace herd output over a number of years, in response to changes such as the control of a disease. Herd models also differ in their emphasis, whether their main objective is to calculate the value of output from livestock (economic models) or whether they include a wider range of biological parameters, especially use of feed resources (bioeconomic models). The ILCA model (von Kaufman, MacIntire and Itty, 1990) is, as its name implies, a bioeconomic model, and was used in the analyses by Itty (1992), Kristjanson et al. (1999) and Woudyalew et al. (1999). Dynamic herd models have been used by Camus (1981), Habtemariam et al. (1983), Brandl (1985), RTTCP (1998) and Doran (2000) among others. Blanc, Le Gall and Cuisance (1995) used the FAO/EMVT livestock model. The Livestock Production and Efficiency Calculator (LPEC) model produced by PAN Livestock Services at Reading University is a static bio-economic model (James, 1995). The model developed by Shaw (1986, 1990, 1992) is more simplistic in its assumptions, since it is deterministic and does not incorporate a direct link with feed resources. Nevertheless it was developed specifically to respond to the analytical requirements of the tsetse and trypanosomiasis problem and includes an option for valuing traction and manure outputs as well as milk, meat and herd growth. It attempts to combine “direct” impacts of controlling the disease on fertility, mortality and milk yield with “indirect” effects, through changes in the production of animal traction, in the number of draught animals kept, in offtake rates (sales and slaughter of animals) and in- and out-migration of animals. The way in which herd parameters change as carrying capacity ceilings are approached can be modelled by varying cattle offtake rates, to simulate animals leaving the area or being sold - the cattle “exported” function, compensating to a small extent for the lack of a bio-economic component. Alternatively, if no cattle are “exported” the effects of overgrazing could be reflected in fertility and mortality. Figure 6 illustrates the basic structure of this model.
FIGURE 6
Structure of a tsetse and
trypanosomiasis-specific cattle herd model
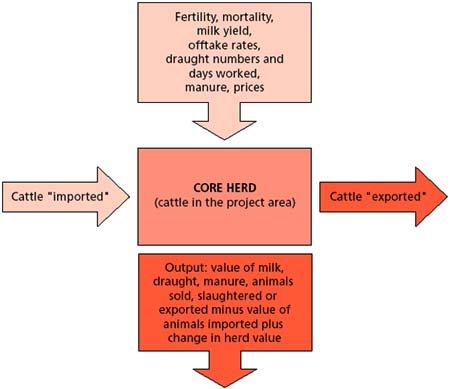
Economic herd models such as this can be used to estimate the benefits of controlling the disease using any of the current technologies, by calculating the “extra revenue” in terms of the difference in output from the herd “with” project and from that “without” project. They can add to this any “costs saved” from a reduction in trypanocide use or the replacement of an earlier tsetse control strategy with a new approach. The model described in Figure 6 also has a benefit - cost analysis component in which the costs of a control strategy can be entered, and compared to the benefits as calculated above.
There are a number of methodological issues that are not altogether resolved. These have to do with pricing cattle, putting a value on herd increase and valuing of inputs made by livestock to agriculture. One issue is whether the value of stock adequately reflects their future ability to produce meat, milk and traction or whether these potential future impacts on agriculture should be calculated separately. Price changes to reflect the quality and weight of the animals produced are also difficult to incorporate. Another issue is how best to price manure and traction outputs. Fortunately, in many parts of West Africa herders are paid, usually in kind, for leaving their cattle on fields and thus manuring the land. There is also a hire market for animal traction. The amounts of such payments can be used in the model to approximate the value of these outputs.
In most cases these analyses of benefits have focused on cattle, their contribution to animal protein production and their impact on the rural economy. Whether or not this is justified is yet another debate. Donkeys are increasingly used for traction, while losses in small ruminants also occur. However, it seems likely that by analysing the impact of the disease on cattle a large proportion of its impact is captured.
The issue of whether or not tsetse control in itself leads to immigration by cattle herders and/or farmers has been much debated and is discussed in Swallow (PAAT, 2000). Reid and Swallow (1998) and Kamuanga et al. (2001c) found that where areas have been closed to settlement for institutional reasons (as in parts of Zimbabwe) the combination of the lifting of restrictions and tsetse clearance will lead to substantial immigration. In the areas studied in Ethiopia, some immigration pre-dated tsetse control, but there was some increase in immigration thereafter as well. However, in Burkina Faso and Côte d’Ivoire they found that migrants were not directly motivated by tsetse clearance. This supports the findings in Bourn (1983) that rates of land-use change in northern Nigeria were much the same in similar ecological zones, irrespective of whether or not tsetse clearance had taken place. Nevertheless, where new migrants or cattle keepers colonise an area and encounter tsetse, heavy losses can take place so that tsetse clearance or effective control of the disease in cattle using trypanocides can be seen as a “facilitating measure” enabling those moving into a new area to avoid heavy losses and be more productive (Kamuanga et al., 2001c). Also, in Zimbabwe Doran (2000) found that farmers moving into the cleared areas were motivated mainly by the greater availability of land and grazing, with 16 percent also mentioning the absence of tsetse. Thus, incorporating cattle immigration in the analysis can be a useful option, but allocating shares of benefits to tsetse control is less straightforward, as land shortage in other areas is a major motivator for emigration.
Another subject which has so far received limited attention is the issue of poverty and control of the tsetse and trypanosomiasis problem. Poverty-focused analyses, based on methodologies such as that developed by Heffernan et al. (2003), are needed here. Given the commitment of donor countries and African governments to the international goal of poverty elimination and the Millennium Development Goals formalized by the United Nations in 2000 (see www.developmentgoals.org) the impact of control strategies on poverty needs further analysis. As stated by Ashley, Holden and Bazeley (1999) the poor often do not benefit from livestock diseasecontrol projects, because the benefits are captured by wealthier farmers, technologies are either not delivered or are difficult for the poor to sustain. There is, however, a growing consensus that many pastoralists can be classed as poor livestock keepers, so that any measure which reduces their vulnerability and improves their income would help reduce poverty. However, beyond this, there are a number of issues which need studying here.
Are trypanocides more or less accessible to the poor than other ways of controlling the disease?
Is it possible to rank control strategies in terms of their pro-poor focus?
Do poor people use animal traction?
Will poor farmers benefit from the greater availability of animal inputs to agriculture?
How herd models can be used to simulate benefits over time
Figure 7 illustrates how herd models can simulate benefits over time. This is the result of a model simulation, based loosely on herds in northern Côte d’Ivoire, using production parameters from Shaw (1993) and current prices. This follows from the approach illustrated in Figure 2, this time illustrating numbers of animals as projected by the model. Three scenarios for the cattle population are analysed:
no change in the tsetse situation, reflecting the “without project” scenario if the fly’s habitat were maintained over the 20 years, with cattle population production parameters retaining their original “with trypanosomiasis” values;
tsetse are autonomously disappearing, so that by year ten the effect of the disease is halved, reflecting the situation if, as shown in the Nash or Rawlings scenarios (see Reid et al., 1999; Nash 1948; Rawlings et al., 1993) human population growth was such that some tsetse populations were reduced;
tsetse are eradicated by year five.
In Figures 7a and 7b the potential benefits to the project, in the absence of any autonomous regression in the tsetse population, are approximated by the total of the two thin areas shaded dark orange and grey at the top of the graph. However, if tsetse are disappearing in the absence of intervention, then the area of benefit is only the small wedge at the top of the graph. This clearly illustrates how benefits are reduced (nearly halved in this case) if work to eradicate the fly simply accelerates an already ongoing process. However, this can still be highly beneficial, for example such a situation yielded high benefit - cost ratios in northern Nigeria (Putt et al., 1980). If it were assumed that tsetse would disappear altogether within the specified time horizon, the resulting reduction in benefits would be even more marked. The range of situations that could be simulated in this way is obviously very large (see below, “Results of simulations”, page 50, for more examples). The size of the large triangle at the bottom of the graph reflects the extent to which existing herds are growing in the absence of control, in the case of the Côte d’Ivoire herds this was at over 2 percent per annum but, as illustrated in Figure 2, this is not necessarily the case.
FIGURE 7A
Cattle numbers with and without tsetse
control
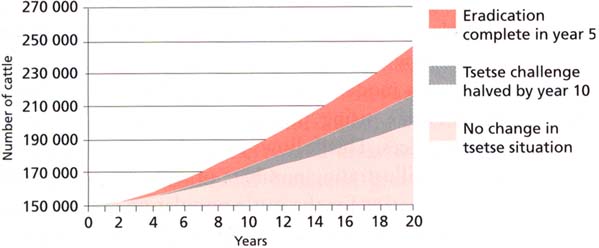
Note: Based on an area of 10 000 km2, containing 10 cattle per km2 at the start of the project.
FIGURE 7B
Cattle numbers subject to a carrying
capacity ceiling with and without tsetse control
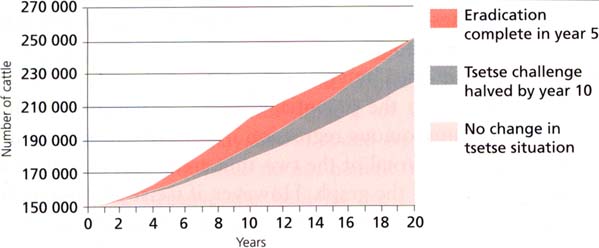
Note: Based on an area of 10 000 km2, containing 15 cattle per km2 at the start of the project.
Analysing the factors influencing the level of benefits obtained from tsetse and trypanosomiasis control
As the costs of tsetse control change with changes in human population density, so do the benefits. Figure 8 shows the curve that was derived by Shaw (1986), after modelling different categories of benefits from tsetse control, including herd cattle production, immigration by people, immigration by cattle and the use of draught cattle. The human population density at the start of the control programme is shown on the x-axis. The y-axis shows the discounted total value of benefits (valued over 20 years in this case). Thus, each point on the curve represents the telescoped sum of the potential benefits of controlling the disease over 20 years. (This is different from the approach used in Figure 7 where these were calculated on a year-by-year basis and in Figure 2 where the possible evolution of benefits over time was shown, both Figures thus tracing output obtained “with” and “without” a project over a number of years). Box 2 explains the process on which Figure 8 is based, by linking changes in human population density with potential benefits from controlling trypanosomiasis.
FIGURE 8
Relationship between the benefits of tsetse
control and human population density

Source: Shaw (1986)
|
BOX 2
|
Having looked at the factors influencing the levels of costs and benefits over time and in different circumstances, the implications of comparing them, using the principles of partial analysis, need to be examined.
Basic relationships
Following on from the discussions underpinning Figures 4 and 8, the next step is to superimpose the graph for benefits on that for costs, as shown in Figure 9. This points to the likely existence of two turning points in the economics of long-term tsetse control operations:
1) when human population density and the associated cattle populations reach a critical size such that there are sufficient benefit units to justify tsetse control;
2) when human population density has started to affect tsetse habitat so that challenge has been lowered, draught cattle numbers have reached their likely upper limit and herd cattle numbers have ceased to expand as they have reached carrying capacity limits.
FIGURE 9
Relationship between tsetse control costs and
benefits and human population density for long-term projects
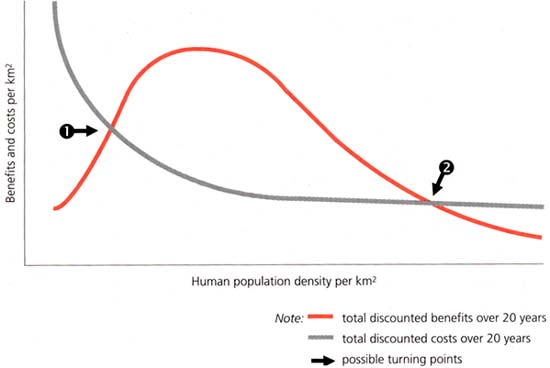
Source: Shaw (1986)
However, short-term tsetse control operations may still be profitable beyond (that is to the left of) point 1), on the assumption that they involve either lower costs and/or a shorter time period. Similarly, small-scale and much targeted control operations may sometimes be feasible beyond (that is to the right of) point 2).
Translating this into real situations, what is implied is that in West Africa, there exists an area between these two limits where sustained control or elimination of tsetse is most likely to be profitable. The population limits are difficult to fix, and there is, as always with this disease and vector, a danger in generalizing the situation. The modelling for northern Nigeria (Shaw, 1986), based on cropping intensity and land use in the tsetse-cleared areas, indicated that the lower turning point was probably between 5 and 10 people per km2, and the higher point between 40 and 70 people per km2 (neatly spanning the limits proposed by Nash, 1948 and Rawlings et al., 1993, as used in Reid et al., 1999). However, although population expansion in northern Nigeria has foreshadowed what might happen elsewhere in West Africa, this modelling exercise was undertaken some time ago, and may be fairly specific to the location and relate to somewhat more arid areas than those presently being considered. Nevertheless, it is worth recalling that Putt et al. (1980) and Bourn (1983) documented similar demographic and land-use changes in the Lafia region of the Nigerian subhumid zone.
For the purposes of the present exercise it is worth noting that:
these turning points probably exist for most tsetse and trypanosomiasis situations;
and, more importantly, while approaching the problem in a different way, they point to the same candidate areas as the GIS studies (Hendrickx, 2001), these being the locations in the moist savannah zone where agriculture and livestock production is expanding.
This analysis also introduces a time dimension over and above that provided by the herd model. With expanding human populations, the x-axis can be interpreted as not only showing at what starting point human population density intervention might be cost effective, but also when this is likely to be appropriate, since human populations are growing over time.
Obviously the shape and position of the curves will vary with different situations and long-term tsetse control strategies, some of these possible variations are illustrated in Figure 10.
a) Some tsetse control strategies (high-cost eradication, ongoing barrier costs, an expensive control strategy) are so expensive that the costs will always exceed the benefits, or conversely the area being analysed offers little scope for rural development so that benefits will always remain lower than costs.
b) In some situations, the window of opportunity, or the range where benefits exceed costs, may be very narrow.
c) Conversely, the range where benefits exceed costs may be fairly broad.
d) Alternatively, it could be that above a certain human and livestock population density benefits always exceed costs, perhaps because without control riverine flies will remain to maintain the disease at high population densities, or because agriculture is dependent on traction and the control of the disease, or because of the presence of sleeping sickness. There would, however, need to be concrete evidence that a given area really falls into this category.
FIGURE 10
Variations in the relationship between costs
and benefits of tsetse control over time with changing human population
density
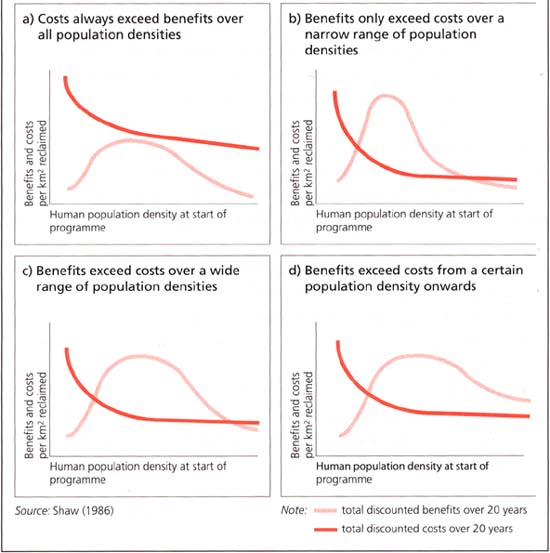
Source: Shaw (1986)
Results of simulations
To illustrate how the use of herd models in a partial analysis framework can inform some of the decisions to be made, the herd model described above in the section “How herd models can be used to simulate benefits over time”, page 43, was used in 48 runs to assess the profitability of tsetse eradication versus trypanocide use. As stated above, there are numerous possible combinations (cattle breed, starting human and livestock population densities, tsetse challenge, control strategy, time frame, etc.). Accordingly, for a hypothetical area of 10 000 km2, this analysis covered:
sedentary herds, with mostly taurine or crossbred zebu - taurine animals, loosely based on herds in northern Côte d’Ivoire;
areas of low to medium trypanosomiasis challenge, very loosely defined;
current prices for livestock outputs and trypanocides;
costs of tsetse eradication and barriers as postulated by Budd (1999);
two control strategies: the use of drugs versus tsetse eradication, with a high- and a low-cost strategy for each;
three starting cattle population densities: 5, 10 and 15 per km2, with a low carrying capacity threshold of 25 per km2.
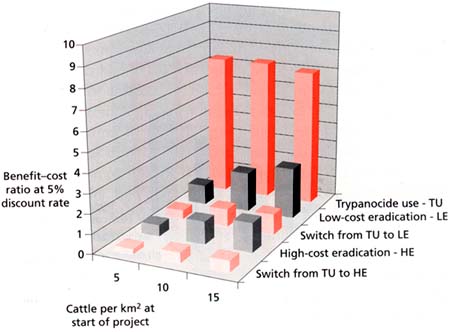
The results of the analyses are shown in Figure 11. This analysis focused on a key issue debated by decision-makers, that of implementing tsetse eradication in areas where farmers are currently controlling the disease using trypanocides. In this context it looked at three control scenarios:
eradication, yielding the full benefit of completely controlling all effects of the disease in a defined area;
the likely current scenario, taking forward the discussion above in the section “How herd models can be used to simulate benefits over time”, page 43, by building on the knowledge of current drug use obtained from recent studies (Blanc, Le Gall and Cuisance, 1995; CIRDES, ILRI and ITC, 2000; Doran, 2000; Kamuanga et al., 2001a; Pokou, Swallow and Kamuanga, 1998), the assumption made is that farmers treat their valuable animals (cows and draught males) methodically, thus dealing with a significant proportion of the losses;
a partial analysis looking at the benefits of switching from targeted use of trypanocides by farmers to tsetse eradication.
FIGURE 11A
Lower challenge situation: tsetse
eradication versus trypanocide use
Note: Eradication is assumed to remove all effects of the disease from all cattle within five years, high cost is US$2 500 per km2, low cost is only US$1 300. Trypanocide use targets cows and draught males and removes three-quarters of the disease effects from these animal categories. Trypanocide use = two doses a year for all cows and draught males, equivalent to 1 dose a year per head of the herd. Time frame was 20 years.
FIGURE 11B
Higher challenge situation: tsetse
eradication versus trypanocide use

Note: Eradication is assumed to remove all effects of the disease from all cattle within five years, high cost is US$2 500 per km2, low cost is only US$1 300. Trypanocide use targets cows and draught males and removes one-half of the disease effects from these animal categories. Trypanocide use = three doses a year for all cows and draught males, equivalent to 1.5 doses a year per head of the herd. Time frame was 20 years.
A selection of the outputs produced is shown in Figure 11. This shows outcomes for different levels of challenge and different levels of trypanocide use. Obviously, the assumptions underpinning the analysis can be criticized and improved upon.
However, the results, as shown in Figures 11A and 11B clearly illustrate some important trends.
Under all assumptions, the highest benefit - cost ratio by far was achieved by the strategy currently employed by farmers, very much endorsing the comments in Doran (2000) and CIRDES, ILRI and ITC (2000). The results were obviously very sensitive to the number of doses given, and would change if drug resistance was found to be a major problem.
As would be expected, tsetse eradication became more profitable at higher cattle population densities, since the number of “benefit units” was higher; and the results were very sensitive to the cost per km2 for eradication, but the higher returns are much in line with the results obtained in other studies (Chapter 2). The cost of eradication would tend to be higher in the higher challenge area and, as discussed above at lower cattle population densities (see section on “Tsetse control”, page 27).
The results for partial analysis for undertaking eradication in an area where farmers are already treating their animals (the situation that would be encountered in much of West Africa with costs and benefits as outlined in Table 2) were very variable. For the lower challenge situation, the switch did not yield a benefit - cost ratio greater than 1.0, except for one instance (low-cost eradication replacing trypanocide use with a cattle density of 15 per km2) where it roughly broke even (Figure 11A). For the higher challenge situation, at the two higher cattle population densities (10 and 15 per km2) the switch was profitable, yielding benefit - cost ratios of 2.3 and 3.1 respectively for low-cost eradication and 1.3 and 1.8 for highcost eradication (Figure 11B).
Eradication was favoured by the use of the low discount rate of 5 percent. Looking at a longer time frame of 30 or 40 years would also make eradication relatively more profitable (preliminary sensitivity analyses showed this trend clearly) but it would never reach the benefit - cost ratios achieved by trypanocide use under current conditions. The analysis assumed that barriers were required for the full 20-year period, removal of these after 10 years increased the benefit - cost ratios somewhat, by 0.25 to 0.5. There would also be additional spin-offs from controlling the vector which are not fully captured here; such as benefits for livestock species other than cattle, the potential for using upgraded livestock in some areas, and the effect of inputs to agriculture not fully captured by valuing draught power in this model. In addition, linking the analyses to epidemiological models provides further insights. This was done by McDermott and Coleman (2001). From this they derived “relative rankings of the effect control strategies on reducing disease prevalence” which “were: vector control, vaccination, and drug use, in that order”.
Nevertheless, the analysis above demonstrates yet again that farmers know what they are doing and are behaving rationally under prevailing circumstances and given the tools at their disposal. There are many other situations which could be analysed using this methodology. Two are particularly relevant in the current decisionmaking context.
First, the benefits and costs of cheaper tsetse control, as against eradication methods, need to be analysed in more detail in the West African context, to see which performs better. The high returns from trypanocide use reflect the fact that these drugs are the first-line intervention used to control this disease. They tend to be used in a fairly targeted way, although farmers cannot always be sure that the animals they are treating suffer from the disease. The high returns are also of a level to motivate farmers who, as private individuals in a risky environment, tend to require a higher return than would be expected from a government project. Inexpensive tsetse control technologies provide farmers with an opportunity of reinforcing their efforts to control the disease and, perhaps, of saving some money by reducing their use of trypanocides and also reducing the risk of drug resistance. Most importantly, while eradication is an option controlled by projects and governments, such tsetse control technologies are more accessible to farmers. The costs cited in Table 3 (US$26 per km2 for suppression using traps in Côte d’Ivoire, or US$60 for using pour-ons in Ethiopia) were low, and even if expended annually would compare well with once-off eradication costs (see Chapter 3, “Time value of money”, page 11). Furthermore, to the extent that they can be applied on a small scale, or can involve the farmer, they avoid the problem of overheads discussed above in the section “Tsetse control”, page 27. As well as offering high returns, empowering farmers and supplementing their current use of trypanocides, such schemes can also be seen as a way of working in higher challenge areas or as a transition strategy to be applied in areas where the fly is vulnerable because of the erosion of its habitat. The results from Ethiopia showed a high return to farmer investment, with a benefit - cost ratio of 8.1:1, and an overall project return of 4.3: 1. In the Central African Republic, the benefit - cost ratio to farmers with large herds was 5.9:1 and 3.1:1 to those with small herds (Blanc, Le Gall and Cuisance, 1995). There is a real need for more analyses of this nature, especially for West Africa.
Second, the benefits and costs of tsetse control programmes tend to be studied before programmes are undertaken and then in the decade after they started. This is largely because of the exigencies of project monitoring and evaluation, where funding exists for an initial appraisal and for an evaluation after a certain period has elapsed. While these studies have often included amongst their sensitivity analyses the implications of re-invasion or breakdown of barriers after some time, the actual economic effect of this type of breakdown in tsetse control measures has not been studied in any detail for a real situation. However, there have been many such events across the continent. Breakdowns in tsetse control schemes and re-invasion of eradicated areas are probably characterized initially by farmers suddenly finding themselves confronted with a disease problem which they were unfamiliar with or had forgotten to consider on a daily basis. There would be an interval of heavy losses, while farmers once again took up the reins of control for this disease. Examples of the effects of a sudden increase in the incidence of the disease have been studied, and could be modelled - there is also knowledge of how and when eradicated areas were re-invaded. From this an analysis of the economics of this type of scenario could be constructed and used to inform the current planning exercises. In addition, a revisiting of old tsetse control and eradication schemes and an analysis of the factors influencing their success and failure would thus be very timely.
|
[3] In economics, elasticity is
a measure of the proportion by which one economic variable changes in response
to a proportionate change in another. |