Traditional management methods are mainly based on the theoretical notion of longterm stability of resources. In these circumstances, the exploitation system must find an equilibrium determined by fishing costs and value of catches. Management problems really come down, so to speak, to defining a level of effort where it is possible to reach a number of objectives, and to stay at that level despite a continuous increase in fishing efficiency.
In the case of variable, or unstable stocks, the notion of equilibrium only has any meaning, at best, in the very long term, if it is admitted that a maximum average yield exists, but it is practically useless for management. Rather than the time scales which are relevant for development (5 to 10 years), it should be considered that certain pelagic stocks are in permanent disequilibrium. This involves the risk of uncontrolled development of the fishery, with disastrous consequences for the economy if the stock collapses (cf. anchoveta stocks of Peru, sardine of California, pilchard of Namibia, etc.). The example of the collapse of Ghana's sardinella stocks seems to indicate that the consequences are less serious in the case of flexible small-scale fisheries with multispecific resources.
The main problem for the authorities responsible for managing a fishery with risks of instability is in fact that of regulation of investment, at sea and on land, if stocks become increasingly abundant over a number of years.
The alternative lies between, on the one hand, uncontrolled hyperintensive exploitation of the biological eruption, leading to immediate high profits followed by very high costs for the State and the taxpayer; and, on the other hand, a wise and controlled exploitation policy, extracting only part of the exceptional resources produced by the eruption, but in compensation reducing to a maximum the negative effects and the costs engendered by overcapacity. Bearing in mind the unfortunate consequences of an economic collapse, we will study only the possibilities of controlling the development phase of the exploitation in the case of biological eruption.
The traditional descriptive diagram of the gradual development of a fishery is shown in Figure 20. When the effort is the principal factor of change in the size of the stock, the fishery will pass through stages 1, 2 and 3 to develop and possibly through stages 4 and 5 if the fishing effort is not effectively controlled.
When the environment plays an important role in the determination of recruitment, and therefore of the size of the stock, the development of the fishery will be conditioned by the interaction between the environment and management, and the risks of collapse will be all the greater if the variations of biomass linked to the environment are important and the fishing effort develops rapidly. In the event of unfavourable circumstances arising, the evolution in 5 phases will be stopped and the expansion phase (Stages 1 and 2) will be followed by a stage of collapse.
The following organizational chart (Fig. 21) gives a very schematic representation of the process of interaction between management and environment during the course of a fishery, from Phase 1 (underdeveloped) to Phase 5 (collapse) and possible reconstitution.
This is a simplified diagram, of which a more realistic and more complex version is given in Annexes 1 and 2. It is, however, enough to show that in the absence of regulation of effort (direct or indirect), there is a high risk of unstable stocks collapsing. It also indicates that risks are reduced but not suppressed by management, and that they exist even in the absence of fishing, although to a lesser extent.
In the diagrams shown in Annexes 1 and 2, consideration is given to factors such as profitability, the action of the environment on the survival of larvae, the need to conserve a minimal reproductive biomass, the possibility of blocking the fishing effort, but also that of optimizing it permanently, compensating for the inevitable gains in efficiency, or by regulating mesh sizes and fishing seasons, for example. The variation of catchability depending on the biomass, an important factor for small pelagic species, is also considered.
These diagrams are obviously, despite their apparent complexity, simplifications of reality. They do not take into account all the human factors and the factors of multispecific interaction. They do, however, offer a representation which illustrates some of the mechanisms leading to the instability of certain fisheries, and the high risk created by the combination of variable biological production and the absence of effective control of catching methods.
Let us take the viewpoint of a coastal State managing a resource that belongs to it. The fishing system, like a predator confronted with the problem posed by a variable resource in abundance, could in theory react as follows:
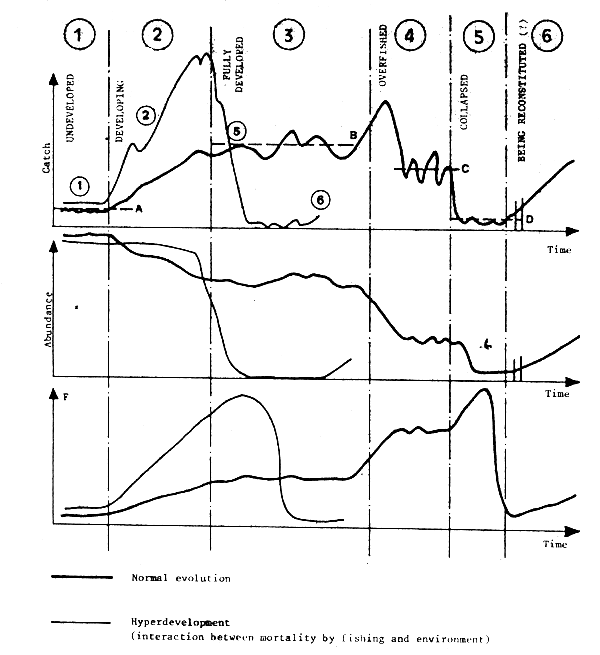
Fig. 20 Stocks of evolution of a fishery. Thick lines: traditional situation where the effort acts alone on the size of the stock Thin lines: hyperdevelopment situation linked to an eruptive phenomenon The horizontal lines A, B, C and D represent pseudo-stationary states of the fishery
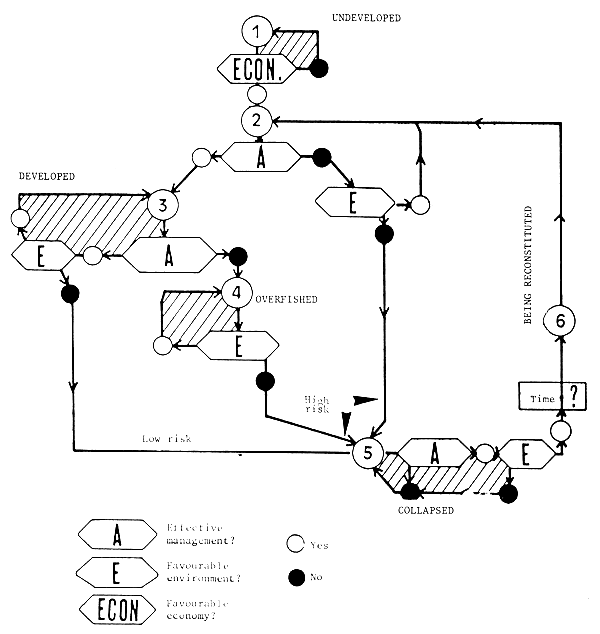
Fig. 21 Schematic representation of the Management/Environment interaction. The 6 phases numbered from 1 to 6 refer to Fig. 20. The pseudostationary states are represented by hatched areas - (Source: Csirke, 1984) - Sea also Annexes 1 and 2
vary its own numbers (and fishing power), with a certain time lag;
stabilize its numbers by finding substitute prey, whether of the same type but elsewhere (migration), or of a different type but in the same place (change of prey).
The national system of exploitation would be authorized to vary its fishing power, but in the framework of well-defined constraints, to avoid a damaging overcapacity. Figure 19 shows (at the bottom) that fishing effort could be increased at the beginning of the ascending phase when the income grows, but that it should begin to decrease before the peak of the biological eruption is reached.
It would be economically preferable to use the technological flexibility of exploitation to increase the catching ability of the fleet without increasing the numbers of fishermen. The regulation of effort could be obtained through a system of annual quotas (see Paragraph 5.3) in the context of a general limitation of fishing effort.
The level of fish processing raises particular problems because it is more rigid. An improvement in techniques is perhaps inevitable in the case of eruption, but large-scale changes, particularly irreversible ones, should be avoided.
At all levels, decisions should be based on awareness that a biological eruption is ephemeral, and the need to manage the fishery for the long-term good of the whole country. The main difficulty for the authorities responsible for management is to resist pressure by industry, motivated by short-term considerations. A maximal ceiling for effort, not to be exceeded whatever the evolution of the stock, should be defined in advance.
It could appear preferable, to catch the exceptional production and the potential profits it implies, to use a fleet with a large radius of action (a “migratory predator”). The perception of fishing rights would make it possible to take advantage of the exceptional profit (the fish is not given away but sold on the spot) without investment. The consequence would, however, be a reduction in the additional direct profits that the national fleet could obtain if it exploited the same resource, because the yields obtained would be reduced by the foreign fleet. It may be said that in this case the exceptional profit is totally or partially appropriated by the State instead of by the national shipowners or, which is more serious, squandered in overinvestment.
Just as a predator changes prey when its abundance falls below a certain level, so the system of exploitation could be developed, retaining sufficient flexibility to exploit without catastrophic changes in numbers, a collection of species whose total biomass is considered more stable than that of its specific components. This would in fact mean the optimization of a strategy that the fishing system already uses in the absence of management, but in a way which is sometimes inefficient and costly for the taxpayer.
It would be necessary in this case to set a ceiling for fishing effort globally, at a level considered sufficient to exploit all the small pelagic species availble (cf. Paragraph 5.4.1). It might be necessary to establish quotas per species, to avoid the concentration of the fleet on one species alone in periods of biological eruption.
The history of unstable fisheries shows that usually, when the biomass decreases very rapidly, it is already too late to act and avoid the biological and economic collapse, if the phenomenon has not been anticipated (Fig. 19):
on the economic level, the problem is to save what can still be saved and to look for new terrains (in the widest sense) for exploitation;
on the biological level, pressure on survivors must be reduced as far as possible; mortality of juveniles per fishery must be reduced (if possible to zero); sanctuaries should perhaps be provided (by closing fisheries altogether in coastal areas); any catch, even secondary (moratory), of the species in question, should be controlled and, if possible, prevented. These measures would provide the best chances of reconstituting the stock. It is clear that, on the economic level, the revival of the system of exploitation after collapse will not be achieved purely and simply by reversing the course followed during development.
It is also clear that this return to normal implies, paradoxically, additional costs, usually for the State. On the biological level, it must be emphasized that the reconstitution of the stock does not seem to be either automatic or immediate. It seems that the reconstitution is easier if the collapse is minor(or if the biomass has not been forced below a certain critical level).
There is a risk that, for a long time, the collapsed stock will remain at a very low level, more or less stable, even with Draconian management (probably difficult to implement efficiently), if the stock has been forced to a level of abundance where it is dominated by other species, or to a level where its spawning behaviour is disturbed, or again if its reconstitution depends on the reappearance of specific climatic conditions.
The main management problem posed by unstable stocks differs from that of stable stocks, first of all because of the special difficulty of controlling the intensive development phase and the resulting dangers. Regulation of effort (and therefore of development) could be envisaged in two different and complementary ways.
The State should effectively control development of the fleet. This is not an attack on freedom of enterprise but an essential safeguard for the interests of the nation as a whole (which is left with the bill for the economic collapse). A maximum global level (“ceiling”) of fishing effort should therefore be defined for all the small pelagics, and therefore a maximum fleet size, according to criteria to be defined. This ceiling could be revised periodically. A fixed periodicity, for example, every five years, would prevent excessive pressure being exercised on the administration for “continuous” revisions.
A quota system would be established.
To avoid sterile competition and an arms race, quotas could be established by region and by port (by country, in the case of shared stocks).
To avoid concentration on one species, annual quotas per species could be established.
To adjust catch rates, annual catch quotas could be defined, using for example, the model proposed by MacCall (1980) for the California anchovy (Fig. 22). This model closely follows the standard production model, but is based on a different representation of the same theory, to the extent that biological production (and therefore the balanced catch) is represented directly as a function of the biomass and not as a function of fishing effort (Fig. 22A). Schaefer's linear model forecasts a parabola passing through a maximum for B = Bmax = 0.5 ∞, where B∞ is the biomass of the virgin stock. Each point of the curve is an equilibrium point, and the line joining the origin at this point (OA) to a slope equal to C/B, that is to say, equal to F, mortality by fishing. It may be seen in particular in Figure 22A that the line joining the origin to the summit of the parabola has a slope equal to FMSY (in reality, if catchability varies with the biomass, there would be a curve (OA'))MSY.
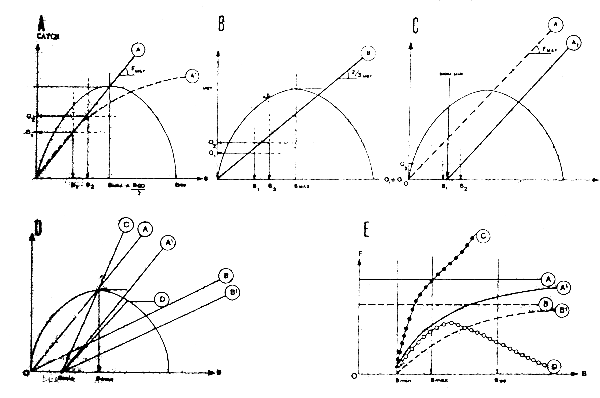
Fig. 22 Definition of annual quotas of anchovy in California (following MacCall, 1980) - A: objective = MSY - B: objective = 2/3 MSY - C: constraint of minimal biomass - D: var=ious possible quota lines - E: vectors of F resulting from D
The advantage of this model is that it is directly expressed in terms of abundance. If the objective of management is to fish to the level of the maximum theoretical production, the line OA could be used to determine the variable annual quotas Q1, Q2, etc., in the light of the changes of abundance B1, B2, as indicated in Figure 22A1. If the objective is to take out only two thirds of the maximum possible to minimize biological risks, a line of quotas with a slope equal to two thirds of FMSY will be chosen (Figure 22B) for more prudent management.
In the two cases described above, the authorized quotas change proportionately to the variations of the obverted abundance. A more conservative process of determination of quotas could be defined with, for example, a more rapid reduction of quotas than the decrease in stock and a nil quota as soon as the stock is below a predetermined value (Bmin) defined, for example, in such a way as to conserve a minimum spawning stock (Fig. 22C). In this case the line of the quotas used (OA1) would be parallel to OA and would lead to even more conservative quotas. In the case represented in Figure 22C, the quota Q1 corresponding to biomass B1 is nil since B1 < Bmin.
This model can be used to define quotas for very complex strategies for regulating fishing effort. Figure 22E shows regimes of exploitation (F authorized depending on the evolution of the biomass) corresponding to different lines of given quotas in Figure 22D. This allows for the possible need to reduce F by the strong values of B so as to conserve the very necessary large buffer biomasses, to conserve a minimal spawning biomass (which is one constraint of the model), to reduce F more rapidly than the biomass when the latter decreases, and to stop fishing entirely when the minimal biomass is reached, etc. This version of the model is in theory relatively robust if there is an error of determination of the equilibrium curve. In fact, the successive quotas will involve the displacement of annual couples (biomass, catch) approximately the whole length of the line of quotas, in search of the equilibrium point at the intersection of the latter and the curve.
If the theoretical equilibrium curve calculated is grossly mistaken, the points observed would be displaced toward an unexpected equilibrium point at the intersection of the chosen line of quotas and the equilibrium of true production, thus indicating the error made. The risk of seriously degrading the stock because of this kind of error is therefore limited. It is still more so if a constraint of minimal biomass is adopted.
This robustness is, however, only theoretical if it is admitted that the stock undergoes variations of abundance of natural origin. In fact, the model recommended by MacCall is determinist to the extent that it is based on only one production curve. In the case of important and autocorrelated fluctuations in the biological capacity of the environment, it may be estimated that there is no longer one curve alone, but a family of curves to represent the stock in its different states. With the procedure described above, annual quotas would therefore tend to be systematically over- or underestimated for several years, and a long period of observation would be necessary before the form of the average longterm curve could be defined. In the meantime, these essential errors could be greater depending on the variability of natural production (Fig. 23).
The problem thus raised is the classic but usually neglected or misunderstood problem of the (difficult) use of a Schaefer model, that could be called strategic, for tactical application. It is a strategic model because it was originally conceived by its author to help in the definition of long-term exploitation objectives (MSY, 2/3 MSY, maximum use, maximum profit, etc.). It is at present used for tactical purposes when used in the short term to calculate the level of effort or of catch to be observed the next year (fixing of quotas).
The solution to the problem would lie in the addition to the model of another relevant variable upwelling index, for example, to make it more predictive in the short term and transform the “white noise” or unexplained variance by the classic relation into usable information. The solution could also lie in more complex simulation models.
Reduction of uncertainty in the case of unstable stocks implies, however, additional research costs and it will be important to develop procedures optimizing the risk/cost ratio.
1 Abundance can be measured by acoustic surveys, for example
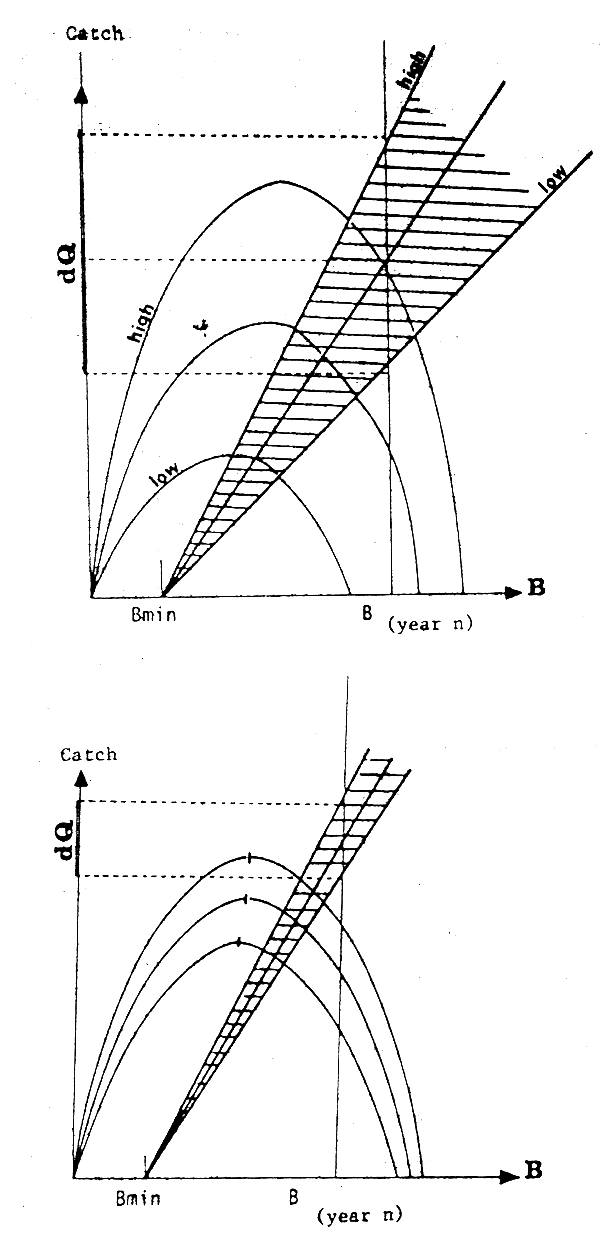
dQ= Potential error in determination of the quota for year n+1
Fig. 23 Effect of interannual variability on the p-recision of the calculated quotas
The model used in California does not perhaps solve all the problems raised, and much progress remains to be made, in particular in countries where research does not have years of experience and data behind it.
This model has the advantage that it can be temporarily established with incomplete data (concerning minimal biomass, for example, which could be arbitrarily fixed). The line of quotas may take various forms and allow for various strategies. It could be different for a stock which is increasing, and for the same stock when it is regressing. The constraints and safety limits of the model and of management can be established in advance, in agreement with administration and industry, facilitating implementation in periods of sudden crisis.
The preceding model makes it possible to use qualitative or approximate information concerning, for example, the form of the relation between catchability and abundance (if it is not constant, the line of determination of quotas will be a curve and not a straight line), the exact form of the model, the minimal biomass, the positive effect of the existence of a buffer biomass. The use of approximate criteria will, in these conditions, enable us to establish an approximate but flexible and relatively sound management, reducing the risks of collapse or improving the chance of reconstitution.
However, in this case as in all those where some uncertainty remains at the level of data, the degree of approximation that the scientist may allow himself will depend on the authorities' and industry's real desire for management. If there is complete agreement (collapsed stock, for example), approximations will be easily accepted and management conducted at a lower research cost.
If, for various reasons, the authorities and/or industry do not really wish to take the necessary decisions, conflicts may be foreseen on the validity of the model and the parameters, and the simplicity of the approach will then become a defect. The requirement of great scientific precision in the parameters will make the model inapplicable within the given time limits, or the cost of research prohibitive.
In this sense, it may be said that the cost of usable scientific advice is inversely proportionate to the will to manage and to the level of risk accepted.