The aim of the preparation module is to estimate the numbers of salmonellae in broiler chicken meat prior to consumption.
Preparation steps
The preparation process begins at the point the chilled or frozen broiler chicken, whole or portions, is removed from the refrigerator or freezer, respectively. Frozen whole broilers and portions must be thawed, but then preparation steps for both frozen and chilled whole broiler are essentially the same. Figure 6.6 summarizes common preparation steps. In the following module description, the case of whole broilers is considered. However, a similar approach can be applied to chicken portioned, provided that time and temperature data are available to characterize the storage, thawing, preparation and cooking pathways.
Figure 6.6. Preparation pathways
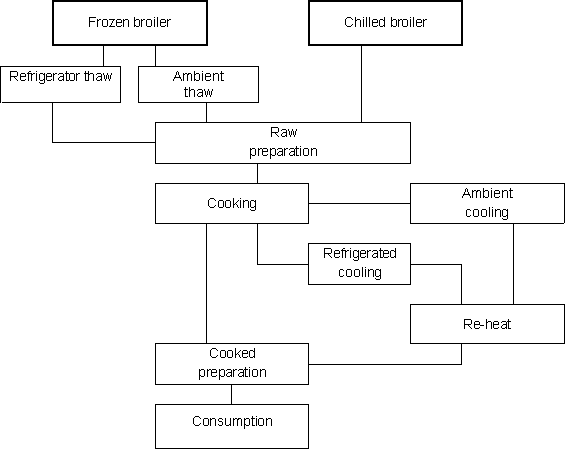
Thawing
Retailers of frozen poultry recommend that a frozen broiler chicken should be thawed overnight in a refrigerator. This is to maintain the surface of the broiler at a low enough temperature to prevent the growth of bacteria. However, in reality, broilers are often thawed outside a refrigerator or in an oven or microwave. If thawed at ambient temperature, the surface of the broiler can approach moderate ambient temperatures and because thawing often requires several hours there is potential for bacteria to grow on the surface. Thawing a frozen broiler in a heated oven takes a shorter period but surface temperatures are higher and bacteria grow more quickly. Thawing a broiler in a microwave creates an uneven heating pattern that again raises temperature and growth rate. This is offset by the reduced time-scale, although uneven thawing can leave frozen areas of the meat that can prevent adequate cooking. The thawing process also causes drip loss and this contaminated fluid can be an additional hazard during raw preparation.
Raw Preparation
Raw preparation involves a considerable amount of handling and hence cross-contamination is a serious hazard. Bacteria present on the meat can be transferred to hands, cloths, utensils and surfaces during the process. These items then become a source of contamination for ready-to-eat food in the kitchen. The preparation of the broiler chicken will also influence the cooking step. For example, a stuffed bird may take longer to cook than one where the cavity is open.
Cooking
Cooking is a critical step in the process. Thorough cooking should kill all the bacteria on and in a broiler. However, low cooking temperatures or short cooking times can result in undercooked meat with potentially live bacteria. The probability that bacteria will survive in these circumstances depends on the degree of undercooking and the bacterial load on the raw broiler. If cooked correctly, the meat should be free from bacteria at the point of consumption.
Cooling and re-heating
It is not uncommon for cooked meat portions, or even the whole cooked broiler chicken, to be cooled, stored, then eaten later, either re-heated or not. If carried out correctly, this process should not be hazardous. However, if the cooked meat is not cooled in a refrigerator but left to cool at ambient temperature, then any bacteria that survive cooking or are transferred by cross-contamination can grow, often quickly. If the meat is not re-heated then there is no opportunity to reduce the bacterial load. If the meat is re-heated thoroughly, then these bacteria will again be killed and the product should be safe. Obviously any less than thorough re-heating, as with cooking, may fail to kill all the bacteria. If the product is cooled quickly to refrigerator temperatures and stored chilled, then the product should be safer than cooling at ambient temperatures. There are numerous documented cases of food poisoning attributable to poorly controlled cook and chill processes.
Meal preparation
Preparation of the cooked broiler can involve processes like carving and dressing. The main hazard here is the potential to contaminate the meat with bacteria. Cross-contamination caused by poor hygienic practices may introduce bacteria onto a product that should be free from them following a correct cooking process.
Data requirements, models available and data
General hygienic practice studies
Table 6.21 indicates research into general food safety practices in the home. These studies give an indication of how many consumers may handle food in an unsafe manner. The studies selected for Table 6.21 are a cross-section of the types of studies that have been conducted. Data from this type of work can be used in an exposure assessment to evaluate the probability of unsafe practices occurring in the home.
Table 6.21. General quantitative surveys of hygiene in the home.
|
Study |
Subject numbers |
Data type |
Comments |
|
Worsfold and Griffith, 1995 |
NA(1) |
Riskscores |
Model for assessing food safety behaviour |
|
Altekruse et al., 1995 |
1620 |
% respondents to food safety questions |
Telephone survey |
|
Scott, 1996 |
NA |
Various |
Review article |
|
Worsfold and Griffith, 1997a |
108 |
% subjects displaying unhygienic practices |
Direct observation in situ |
|
Jay, Komar and Govenlock, 1999 |
40 |
% subjects displaying unhygienic practices |
Direct observation via video |
|
Schutze et al, 1999 |
NA |
Salmonella serotype, culture sources % |
Investigation follow-up after salmonellosis diagnosis. |
Notes: (1) NA = not applicable.
Thawing
For an exposure assessment model, any changes in the number of salmonellae during the thawing process can be predicted using the survival and growth models discussed in Section 6.2.5, provided that adequate data are available to describe the temperature changes.
Studies on the thawing of broilers are often carried out by broiler chicken processors and retailers for the development of safe thawing instructions. These data can often be obtained by risk assessors on application to the company. Unlike freezing and chilling where the warmest part would be the deep muscle, the reverse is true of the thawing process. It is important therefore to measure the thermal profile at the surface of the broiler as well as in the deep muscle (Table 6.22). Unfortunately, these measurements are rarely taken. Such is the emphasis for developing thermal profiles for cooking where the coldest spot is measured (the geometric centre), that workers often use the same approach to measure thawing. In these studies the emphasis is on whether thawing is complete, which is essential for the subsequent cooking process. However, few data in the literature are available to describe the surface temperature where Salmonella, if present, can begin to multiply. It is possible to use thermodynamic models for thermal diffusivity to calculate a surface temperature given air temperature (Brown et al., 1998).
Table 6.22. Example of data on thawing of a 2300-g raw, frozen broiler chicken carcass.
|
Process step |
Deep muscle temp. (°C) |
Surface temp. (°C) |
|
Start thaw in packaging at ambient temperature |
-17.3 |
-16.0 |
|
After 24 hours in packaging |
-1.9 |
1.4 |
|
After 29 hours (with 5 hours in ambient conditions, removed from packaging) |
0 |
11.3 |
SOURCE: Provided by Christina Farnan, Carton Group, Cavan, Republic of Ireland.
Bryan and McKinley (1974) studied the preparation process for whole frozen turkey and produced detailed time and temperature profiles for all processes, including thawing. However, they reported only deep muscle temperatures and the air temperature. For a 20-lb [9 kg] turkey, they found that after 40 hours thawing in a refrigerator at ~4°C the deep muscle temperature was only -2.8°C. At ambient temperature (~24°C), the deep muscle temperature was 0°C after 9 hours and 10°C after 18 hours. The surface temperature in this latter case was 10°C after 5 hours and 16.6°C after 22 hours. This demonstrates that the surface temperatures can be relatively high by the time the turkey is thawed. For broilers where weights are lower, the thawing time would be reduced, but the surface temperatures after similar periods are likely to be the same or slightly higher, due to the reduced mass of the bird.
It is important to validate any predictions of growth during thawing and at least one suitable study is reported in the literature. Data on the growth of Salmonella following thawing was generated in minced chicken substrate (White and Hall, 1984). Such data could be used to develop a model for frozen storage, periods of freeze-thaw and thawing, but this type of model development is outside of the scope of the current exposure assessment. The White and Hall data show that the numbers of S. Typhimurium decreased during frozen storage by approximately 99% after 168 days of storage, but by only 90% for S. Hadar in a similar period. They also showed that the numbers of S. Typhimurium increased by 1.8 log cycles after 24 hours thawing at 20°C and by 2.93 log cycles after the same period at 27 C. S. Hadar grew by 2.87 log cycles after 24 hours thawing at 20°C and by 5.4 log cycles after the same period at 27°C. These data on thawing can be used to validate the growth models selected, given the thawing profiles reported.
Preparation handling of raw chicken
Handling which is typically carried out at ambient temperatures can transfer bacteria via cross-contamination of the hands and food preparation environment and especially if prolonged, this is another factor that may lead to growth of salmonellae.
There are few data available in the literature on time and temperature studies during preparation. Data on the time taken to prepare poultry and the temperature changes were reported by Garey and Simko (1987).
Several studies of cross-contamination have been conducted, but these consider general contamination of the food environment rather than the contamination attributable to a specific process such as preparation of chicken (Scott and Bloomfield, 1990; Josephson, Rubino and Pepper, 1997). Others have quantified the incidence of cross-contamination due to specific processes (Humphrey, Martin and Whitehead, 1994; Cogan, Bloomfield and Humphrey, 1999). However, few have quantified the numbers of bacteria that are transferred during cross-contamination. Cross-contamination resulting from the preparation of broilers has been studied (de Wit, Broekhuizen and Kampelmacher, 1979). In an elegant study, they used naladixic-acid-resistant E. coli K12 as a marker organism to artificially contaminate broilers. The spread of this organism during preparation was studied. The cross-contamination rates show that the more direct the contact between broiler and item, the greater the percentage of positive samples from that item. Washing reduces the incidence of cross-contamination, but not completely. In the preparation process, other surfaces, such as water taps and spice jars, also become contaminated, but to a lesser extent, indicating indirect contamination from hands.
For a quantitative exposure assessment model, these data could be used to calculate the probability of cross-contamination by direct and indirect means, which would be more practical than separate calculations for surfaces, utensils and hands.
A measure of the probability of cross-contamination is not sufficient for an exposure model without an idea of the quantity of bacteria involved. Zhao et al. (1998) developed a model system to enumerate bacteria transferred during common food preparation practices. They found that chicken meat and skin inoculated with 106 CFU bacteria transferred 105 CFU to a chopping board and hands, and then 103-104 CFU to vegetables subsequently chopped on the unclean board. Disinfection of the chopping board and hand washing reduced the numbers of bacteria by 1-2.8 logs and reduced the incidence of cross-contamination of the cut vegetables (52%: no bacteria; 33%: 10-50 bacteria; 5%: 100-200 bacteria).
These data can be used as the basis to estimate the numbers of bacteria transferred to a food by cross-contamination. From the work of Zhao et al. (1998), it appears that bacteria transfer at a rate of approximately 10% between items, e.g. between raw chicken and the chopping board. Direct cross-contamination involves two steps, e.g. raw meat to chopping board, and then to another food item. Hence, the direct cross-contamination bacterial load for the second food item should be a maximum point estimate of 1% of the numbers of salmonellae on the broiler chicken. Indirect cross-contamination involves a minimum of three steps, e.g. broiler chicken to hands, to plate, and then to another food item. Hence, for indirect cross-contamination, the bacterial load transferred to another food item would be a maximum of 0.1% of the salmonellae on the broiler.
Cross-contamination can also occur from inadequate hand washing. Studies on hand washing have shown that numbers of bacteria on the hands influences the number of samples that are contaminated through finger contact (Pether and Gilbert, 1971). Reviews of hand washing practices are available in the literature (Snyder, 1999; Restaino and Wind, 1990; Reybrouck, 1986).
Cooking and thermal death models
Bacteria die when subjected to the elevated temperatures found during cooking. It is widely accepted by microbiologists that bacteria die in a predictable, logarithmic way. This is referred to as first-order inactivation kinetics. The physiological assumption is that there is only one heat target per cell that is responsible for the death of the whole cell. Classically, the death of bacteria has been described by the Arrhenius equation that was developed for first-order chemical reaction kinetics (Equation 6.3):
|
|
Equation 6.3 |
where: Ea = activation energy (J mol-1); A = pre-exponential factor, R = gas constant (8.31 JK-1 mol-1), N0 = initial cell number, N = cell number after time at T, and T = absolute temperature (Kelvin).
However, deviations from the first-order death kinetic model have been observed. Shoulders and tails to the survivor curves are reported. This area has been reviewed extensively (Clark, 1933; Withell, 1942; Rhan, 1945; Cerf, 1977; Casolari, 1994). Several models that have characterized non-linear thermal death curves have used a log-logistic function to describe the data (Cole et al., 1993; Little et al., 1994; Ellison et al., 1994; Duffy et al., 1995; Anderson et al., 1996; Blackburn et al., 1997).
The equation for the log-logistic curve, with a shoulder and a tail, is shown in equation 6.4.
|
|
Equation 6.4 |
where N = cell number after time at the temperature studied, a = upper asymptote of the curve, w = lower asymptote of the curve, s = maximum inactivation rate, and t = time to the point of maximum inactivation rate.
For the present exposure assessment, the traditional log-linear-death kinetic model will be considered, for simplicity. Many investigators do not show the inactivation data for their studies and merely quote D-values (i.e. time for a 90% reduction in the numbers of bacteria at a given temperature). Generally, these workers will use regression analysis of data showing log10 bacteria numbers vs heating time. The equation of the regression line can be used to calculate a D-value over 1 log cycle reduction in the numbers of bacteria. When D-values are calculated for a number of different temperatures, a relationship between the D-value and the temperature can be calculated. Data expressed as the reciprocal of the D-value vs temperature of the D-value can be analysed by regression to give a straight-line equation. This equation can be used to calculate a z-value, which is the temperature change required to bring about a 90% change in D-value. Hence, if the z-value = 10°C and a D-value at 70°C = 1min, then by applying the z-value to the D-value we can see that the D-value at 80oC = 0.1 minute and the D-value at 60°C = 10 minutes. Therefore, with a D-value at a given temperature and a z-value for a bacterium in a given heating medium it is possible to calculate the reduction in the numbers of that bacterium at any other temperature.
Secondary models can be constructed that relate the change in D-value to parameters such as pH and water activity. A model describing the death of S. Enteritidis was developed by Blackburn et al. (1997). This model is comprehensive, covering the effects of temperature, pH and salt on survival. In addition, the model validated well against D-value data derived in whole foods. Unfortunately, this model is incorporated into the Food MicroModelTM software, which is proprietary.
An alternative approach that has been used in other exposure assessments is to take published D-values for Salmonella in foodstuffs, analyse the data, and determine an average D-value and z-value using the method described earlier (Buchanan and Whiting, 1997). Table 6.23 shows data used in this exposure assessment model for the calculation of an average D-value and z-value (Figure 6.7).
Table 6.23. Data on the inactivation of Salmonella
|
Serotype |
Meat |
D-value (minutes) |
Temperature (°C) |
Reference |
|
Salmonella |
Chicken |
0.176 |
70 |
Murphy et al., 1999 |
|
Salmonella |
Chicken |
0.286 |
67.5 |
Murphy et al., 1999 |
|
S. Typhimurium |
Ground Beef |
0.36 |
63 |
Goodfellow and Brown, 1978 |
|
Salmonella |
Ground Beef |
0.7 |
62.76 |
Goodfellow and Brown, 1978 |
|
S. Thompson |
Minced Beef |
0.46 |
60 |
Mackey and Derrick, 1987 |
|
Salmonella |
Ground Beef |
4.2 |
57.2 |
Goodfellow and Brown, 1978 |
|
S. Typhimurium |
Ground Beef |
2.13 |
57 |
Goodfellow and Brown, 1978 |
|
S. Typhimurium |
Ground Beef |
2.67 |
57 |
Goodfellow and Brown, 1978 |
|
S. Typhimurium |
Skin macerate(1) |
61.72 |
52 |
Humphrey, 1981 |
|
Salmonella |
Ground Beef |
62 |
51.6 |
Goodfellow and Brown, 1978 |
NOTES: (1) from chicken neck.
Figure 6.7. Plot of D-values from Table 6.23 with linear regression model used to subsequently calculate D- and z-values.
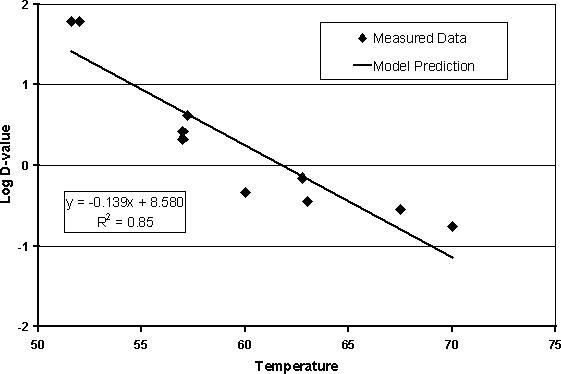
The D-value can be calculated using Equation 6.5:
|
|
Equation 6.5 |
and the z-value is the reciprocal of the slope of the line, Equation 6.6:
|
|
Equation 6.6 |
To utilize the linear model for the thermal death of salmonellae in an exposure assessment model, it is necessary to measure the time and temperature profile for the cooking step. For conventional conduction-limited cooking (i.e. oven roasting, boiling, steaming), measurements are normally taken at the coldest spot, which is the deep muscle tissue of a broiler chicken carcass. However, this does not give information about the temperature at the surface of the carcass, where salmonellae may also be located.
For microwave cooking, where the thermal profile may be uneven, measurements must be taken in a number of places. An exposure assessment should account for differences in cooking methodology and the heterogeneity of temperature that this may cause. Models for microwave cooking are very complex and often require the use of thermodynamic modelling techniques to generate the time and temperature distributions.
Many studies reported in the literature do not contain the thermal profiles. Some report end-product temperatures and cooking time (Baker, Poon and Vadehra, 1983; Schnepf and Barbeau, 1989). Table 6.24 shows some publications where appropriate data are given.
Example data have also been supplied by a manufacturer of cooked chicken products (personal communication). Data for cooking of chicken drumsticks are summarized in Table 6.25.
Table 6.24. Studies on thermal profiles for cooking of poultry.
|
Study |
Item cooked |
Cooking method |
Parameters measured |
|
Bryan, 1971 |
Whole turkey |
Boiling and steaming |
Deep muscle, surface and external temperature |
|
Bryan and McKinley, 1974 |
Whole turkey |
Oven roast |
Deep muscle, surface and oven temperature |
|
Lyon et al., 1975 |
Chicken thighs |
Boiling |
Internal temperature |
|
Ibarra et al., 1999 |
Chicken breast |
Oven roast |
Infrared surface and internal temperature |
|
Chen and Marks, 1997 |
Chicken patties |
Oven roast |
Surface, interior and oven temperature |
|
Chang, Carpenter and Toledo, 1998 |
Whole turkey |
Oven roast |
Various points |
Table 6.25. Example thermal profile data on roasting chicken drumsticks.
|
Time (minutes) |
Time of the temperature block (minutes) |
External temp. (°C) (mean of 2 measurements) |
Internal temp. (°C) (mean of 6 measurements) |
|
0 |
5 |
12.6 |
14.9 |
|
5 |
5 |
13.0 |
14.2 |
|
10 |
5 |
136.6 |
13.7 |
|
15 |
5 |
161.2 |
27.8 |
|
20 |
5 |
150.0 |
43.2 |
|
25 |
5 |
150.7 |
56.2 |
|
30 |
5 |
164.0 |
68.6 |
|
35 |
5 |
166.1 |
78.0 |
|
40 |
5 |
168.6 |
85.8 |
|
45 |
5 |
166.3 |
83.7 |
|
50 |
5 |
176.3 |
93.3 |
|
55 |
5 |
161.4 |
94.9 |
|
60 |
5 |
49.2 |
82.1 |
To calculate the lethal effect of the process shown in Table 6.25, the following approach can be applied:
1. Break the profile up into time and temperature blocks as shown in Table 6.25.
2. Using Equation 6.5, calculate a D-value at a suitable reference temperature within the range of the profile.
3. Use Equation 6.7 to calculate the equivalent process time at the reference temperature for each time and temperature block:
|
|
Equation 6.7 |
where: Etime = equivalent time at the reference temperature; Tref = reference temperature; T = temperature (°C) of the time and temperature block; z = temperature change resulting in a 90% change in D-value, calculated from Equation 6.6; and time = time period of the time and temperature block (in minutes).
4. Use Equation 6.8 to calculate the equivalent reduction in log numbers of bacteria for each time and temperature block.
|
|
Equation 6.8 |
where: Log red = reduction in log numbers of bacteria; Etime = equivalent time at the reference temperature; Tref = reference temperature; and D = D-value.
5. Subtract each reduction from the starting log number of bacteria to determine the number of bacteria surviving the process.
Figure 6.8 shows the application of this approach to the data given in Table 6.25, using the model generated in Equations 6.7 and 6.8 and an assumed starting number of salmonellae of 10 million.
Cooling and re-heating
Providing suitable time and temperature profiles are available, the growth and thermal death models can be used to predict the numbers of salmonellae that may be present after a process. Published time and temperature profiles can be found (Bryan, 1971; Bryan and McKinley, 1974) but, as with all such profiles, data are scarce.
Meal preparation
Meal preparation can involve re-contamination of the cooked chicken from salmonellae present on hands, utensils and surfaces. This can be accounted for in the exposure assessment in a similar manner to the modelling of the raw preparation step. An assumption based on data can be made for the probability of cross-contamination and the numbers of salmonellae transferred (see above: Preparation handling of raw chicken).
Figure 6.8. Cooking temperature profile for a chicken drumstick and the predicted reduction in the number of salmonellae in the deep muscle tissue.

The aim of the consumption module is to quantify the frequency with which broiler meat is consumed in the form specified in the preparation module, and to quantify the portion size.
Consumption studies
One aim of an exposure assessment model is to provide quantitative data to input into the dose-response model. To do this, it is necessary for the exposure assessment to predict the likelihood of human exposure to a bacterial pathogen, and the numbers of the pathogen to which a person may be exposed. So far in this report, tools have been described that enable a quantitative prediction of the number of salmonellae on ready-to-eat broiler chicken meat, and the likelihood that the chicken meat will be contaminated with salmonellae. However, to become exposed to the bacteria, a person must consume broiler meat. Therefore, the number of bacteria that enter the person’s body also depends on the amount of the meat they eat and possibly the frequency of consumption. The final stage in the exposure assessment model is a determination of consumption patterns for broiler chicken meat.
Food consumption patterns vary from country to country, by demographic group, and by age group. Therefore, ideally, countries should determine their own national consumption patterns. Additionally, consumption studies are often undertaken for purposes other than exposure assessment, e.g. nutrition studies. The design of these studies is not necessarily appropriate for determination of exposure to microorganisms from consumption of a product.
Data requirements and available data
Data required for a consumption module would relate to the products specified for the risk assessment, and in the exposure assessment. In this work, consumption data are required for a single serving from whole or portioned broiler chicken, prepared in the home according to the methods used in the previous module.
Commodity consumption data have been compiled and published by WHO (1998). For countries without national studies, this work is a good reference. Unfortunately, because of its general nature, it gives consumption data for chicken meat from all sources on a regional basis. The consumption of chicken meat per day per capita was reported as follows:
|
|
· Middle Eastern diet |
30.5 g |
|
|
· Far Eastern diet |
11.5 g |
|
|
· African diet |
5.5 g |
|
|
· Latin American diet |
25.3 g |
|
|
· European diet |
44.0 g |
These data include meat from whole cooked broilers, but in addition also include servings of cooked minced chicken preparations, pre-prepared commercial meals, and other sources outside the scope of the present exposure assessment model.
A more detailed breakdown of food consumption can often be gained from national nutrition surveys. For example, in Australia, a national survey conducted in 1995 (McLennon and Podger, 1995) classified consumption of whole muscle poultry meat inter alia by age group, sex and socioeconomic group. Table 6.26 summarizes the relevant data.
Table 6.26. Mean daily intake of poultry muscle meat per person in Australia.
|
Male age group (years) |
|||||||||
|
2-3 |
4-7 |
8-11 |
12-15 |
16-18 |
19-24 |
25-44 |
45-64 |
65+ |
19+ |
|
11.3 g |
19.2 g |
26.8 g |
48.4 g |
51.4 g |
73.1 g |
66.7 g |
62.6 g |
45.4 g |
63.3 g |
|
Female age group (years) |
|||||||||
|
2-3 |
4-7 |
8-11 |
12-15 |
16-18 |
19-24 |
25-44 |
45-64 |
65+ |
19+ |
|
8.8 g |
12.5 g |
23.6 g |
29.4 g |
32.3 g |
33.7 g |
31.5 g |
34.2 g |
29.7 g |
32.2 g |
|
SEIFA quintile of relative socioeconomic disadvantage(1), 19 years + |
|||||||||
|
1st |
2nd |
3rd |
4th |
5th |
|||||
|
47.3 |
48.1 |
45.6 |
47.1 |
48.9 |
|||||
NOTES: (1) Based on the characteristics of an area where the person lives. People in the first quintile live in the most disadvantaged areas, whereas people in the fifth quintile live in the least disadvantaged areas. SOURCE: McLennon and Podger, 1995.
These data allow exposure predictions to be targeted to vulnerable groups, such as the very young and the elderly. The study also showed that, in Australia, the consumption of poultry muscle meat was not influenced to any great degree by socioeconomic group.
The single drawback to these data is that the only value reported is the mean daily intake. Reporting the standard deviations of the mean values would allow estimation of the distribution range of size of meals consumed.
In Ireland, the Irish Universities Nutrition Alliance (IUNA) have recently completed a food consumption survey. The primary aim of the survey was to establish a database of the habitual food and drink consumption of Irish adults between the ages of 18 and 64. The Republic of Ireland section of the database contains entries for 958 subjects, but as the data were collected per eating occasion, there are 159 091 entries in the database. The total food consumption for each subject must be taken to represent his or her habitual weekly intake of a given food. The IUNA database was searched for meals where chicken was casseroled, grilled, stir-fried, deep-fried or roasted. Prepared chicken dishes - chicken Kiev, chicken vindaloo, etc. - were excluded.
Of the 159 091 eating occasions entered in the database, 1289 referred to chicken muscle. In real terms, 633 subjects out of a possible 958 consumed chicken muscle at least once per week (66%). Of those consuming at least once a week, it was found that the chicken muscle was consumed on average 2.04 times per week (maximum 7 times; minimum once).
It is worth noting that consumption data is very country specific as consumption patterns may be very different in different parts of the world. Thus, any national exposure assessment should use data specific for that country rather than data from any other country.
Overview
To date, no full exposure assessments of Salmonella in broiler chicken products have been presented, i.e. an exposure assessment that includes all the steps outlined in Figure 6.1 for the production-to-consumption pathway. However, exposure models have been developed for subsections of this pathway. Oscar (1997) considers levels of exposure throughout processing (Module 2 in Figure 6.1) while Oscar (1998) and Oscar (in press) developed models to describe exposure from the point of packaging to the point of consumption (Modules 3 and 4 in Figure 6.1). Brown et al. (1998) consider changes in the numbers of organisms on contaminated raw chicken products following cooking (Module 4 in Figure 6.1).
In contrast, a full exposure assessment has been described for Campylobacter jejuni in fresh poultry (Fazil et al., unpublished; A.M. Fazil, personal communication). Although there are key differences between Salmonella and Campylobacter jejuni, this model can be used as a basis for review.
These models are summarized here with respect to the objectives of the work, and the various methodologies used. It is noted that several of the models consider, to some extent, dose-response and hazard characterization as well as exposure assessment. In such cases, only the exposure assessment part is reviewed. Following each summary, the methodologies are discussed with respect to a full exposure assessment of Salmonella in broiler chicken products.
The models of Oscar (1997), Oscar (1998) and Oscar (in press)
The model of Oscar (1997) is essentially a demonstration tool to illustrate the use of simulation modelling in food safety decision-making. Consequently, real data are not used within the model and hence results do not represent actual estimates of exposure.
The demonstration model considers the prevalence of Salmonella-positive broiler chicken carcasses and the number of organisms per contaminated carcass following each sequential step of processing, as outlined in Figure 6.3. Each step is characterized by two quantitative parameters, the prevalence and the extent of a specific pathogen event. Pathogen events correspond to either an increase or reduction in numbers of organisms per carcass, depending on the step-specific factors. In the model, increases reflect only cross-contamination, hence bacterial growth is not included.
A similar pathogen event approach is used in subsequent models (Oscar, 1998; Oscar, in press). These models commence at packaging of raw chicken and describe changes in the prevalence of Salmonella-positive products and the numbers of organisms per positive product until the point of consumption. Pathogen events again refer to either an increase or decrease in pathogen load, but these subsequent models also consider bacterial growth.
These three models provide simple assessments of exposure. The underlying methodology involves simulation of a random chicken product through various exposure steps.
In general terms, the framework presented in the Oscar models could be used as a basis for development of a full exposure assessment of Salmonella in broiler products. Indeed, in the first instance, it may be possible to combine the processing model (Oscar, 1997) with either of the packaging-to-consumption models (Oscar, 1998; Oscar, in press). However, there are important points that would need further consideration before such use.
First, the model framework describes the inherent variability of the sequential exposure steps. In particular, the probabilities (pi) represent the randomness associated with whether or not the particular pathogen events will occur while the distributions for changes in numbers of organisms describe all possible magnitudes of change. However, it is possible that for Salmonella we may not know the exact values for pi and all possible magnitudes of change. Therefore it is likely that there will be uncertainty associated with these parameters. As is, the model framework does not account for such uncertainty and thus may produce inaccurate estimates of exposure.
The second feature of this framework that should be addressed focuses on the notion of cross-contamination. The model framework for packaging through to consumption does not include cross-contamination to other products or the environment. However, during preparation, for example, such cross-contamination might be very important. Consequently, this approach could underestimate exposure. For the processing model (Oscar, 1997), the methodology used to account for cross-contamination is not explicitly stated, hence it cannot be determined whether or not this would be appropriate in a full exposure assessment.
A final point worth considering is the representation of growth and survival within the packaging-to-consumption models. Growth and reduction due to temperature abuse and cooking, respectively, are not given as time-dependent processes within the models. Rather, the overall change following a period of abuse or cooking is modelled. Although this gives a mechanism for estimating changes in exposure, the effect of different temperature profiles and product specific parameters cannot be investigated. Consequently, investigation of control strategies would be difficult.
In summary, these provide a basis for the development of a full exposure assessment, but issues concerning uncertainty, cross-contamination, growth and decline would have to be addressed before further use.
The model of Brown et al. (1998)
This model considers the prevalence of Salmonella on raw chicken portions and the numbers of organism per contaminated portion. Prevalence is estimated by a point value while a probability distribution is used to describe the variability in the numbers of organisms per contaminated portion. Given the initial level of pathogen on the raw product, the final level of exposure is then determined by modelling the effects of cooking.
The approach used within this model is deterministic in nature. In particular, point values are used for model parameters such as prevalence of contaminated chicken portions, and the heat transfer coefficient. Estimates of exposure are determined by integration over all parameters that are inherently variable, more specifically time, microbial distribution, and measurement of depth into the product. Although this approach accounts for inherent variability, it does not incorporate uncertainty in parameter values. As a result, it does not facilitate the derivation of confidence intervals for estimates of exposure. The authors present several suggestions for including uncertainty that could be incorporated in a full exposure assessment.
There are two main exposure steps in this model: first, the level of raw chicken contamination and, second, the effect of cooking. Cross-contamination within the kitchen, prior to cooking, is not considered. As discussed previously, cross-contamination within the kitchen could be a very important pathway for exposure to Salmonella from raw poultry and thus should be included within a full exposure assessment.
Overall, the framework presented in this model will be very useful for the development of Module 4 (Preparation) (see Figure 6.1) of any full exposure assessment. The framework could also be further enhanced by including uncertainty in model parameters and attempting to model cross-contamination in the kitchen.
The model of Fazil et al. (unpublished)
This assessment is still in-progress (A.M. Fazil, personal communication.). The review presented here considers the information that was available at the time of this review. It is expected that this model will be refined in the future, thus the comments made here may require appropriate modification.
The preliminary model provides a full exposure assessment for Campylobacter jejuni in fresh chicken. All stages from on-farm production to consumption are considered. At each stage, the ‘fate’ of C. jejuni on chickens is estimated with particular reference to surface contamination and the numbers of organisms per contaminated unit (carcass). In this way, changes in prevalence and numbers are described and a final estimate of exposure is derived. As this model considers fresh chicken products, the framework presented provides a basis for the development of an exposure model for Salmonella in the same commodity.
In a similar manner to the model pathway outlined in Figure 6.1, the exposure assessment commences with estimation of farm-level parameters. More specifically, the number of organisms on the skin and feathers of birds is calculated. Estimation is undertaken by determining the number of organisms excreted in the faeces and then assuming that a proportion of these contaminate the external parts of the bird. Consequently, it is assumed that feather, skin, etc., (i.e. surface) contamination arises directly from the birds. Given that within-flock prevalence of Campylobacter is generally very high (Hartnett et al., 2001), this would appear to be a valid assumption. However, for Salmonella, within-flock prevalence is much more variable and it may be more appropriate to consider other sources of contamination.
From the initial concentration of organisms on the exterior of birds at the farm level, changes in numbers during transport and subsequent processing are modelled. The modelling approach considers each step in turn and determines the magnitude of change in terms of either a log increase or decrease, depending on the particular step. The magnitude of change is estimated from several data sets that provide this specific type of information, hence particular reasons for change, such as cross-contamination or wash-off, are accounted for. If equivalent data were available for Salmonella spp, a similar modelling approach could be used. It is of course important to point out one key difference between Salmonella and Campylobacter, that is that conditions during processing that may be favourable for the growth of Salmonella would probably not result in multiplication of Campylobacter.
As changes in concentration are modelled, changes in prevalence of contaminated birds, carcasses or products from farm to the end of processing are also described. The initial prevalence estimate relates to prevalence of contaminated birds on entry into the processing plant, and this estimate essentially describes the probability that any random bird is contaminated. During processing, changes in prevalence have been modelled by initially ranking the different stages according to the extent to which cross-contamination is likely to occur. Based on this ranking, a cross-contamination factor is then assigned to each step. For each step, the resulting prevalence is a function of the prevalence at the start of the step and the cross-contamination factor. Given the generality of the cross-contamination factor approach, it is likely that a similar methodology could be used to model changes in Salmonella prevalence during processing.
Following processing, the time between processing and preparation of the chicken in the home is considered. This period covers both storage and transit. It is assumed that the chicken product remains at refrigerated temperatures and reduction in the number of organisms per day is calculated. This approach, which essentially models survival, is appropriate for Campylobacter. However, for organisms such as Salmonella, growth during storage and transit may be important, depending on whether or not temperature abuse occurs. Consequently, growth as well as survival would have to be considered.
The final step of the exposure assessment models consumer handling and preparation. It is assumed that exposure to C. jejuni occurs via two independent routes: consumption of undercooked chicken and through the raw chicken fluids that may be subsequently ingested through cross-contamination. The models presented for these steps could be adapted for a Salmonella exposure assessment by incorporating species-specific data.
The Campylobacter exposure assessment is a stochastic model. The stochastic component of the model framework describes the variability in changes in prevalence and numbers of organisms throughout the sequential exposure steps. However, as yet, the uncertainty associated with these distributions of change is not accounted for. Given the limited quantitative information relating to changes in prevalence and numbers, inclusion of uncertainty will be important for an exposure assessment of Salmonella.
Overall, the general framework on which the preliminary model of Fazil and collaborators is based could provide a basis for the development of a Salmonella exposure assessment. However, other factors would also have to be included, particularly growth during storage and transport and uncertainty associated with probability distributions to describe magnitudes of change.
To date, no full exposure assessments have been undertaken for Salmonella in broilers. This present report has considered:
What is required for undertaking such assessments.
What information is available.
How the available information meets the requirements.
The following recommendations for directing future work can be made.
(i) Reporting of prevalence at different steps of the full exposure pathway should be encouraged in all regions of the world.
(ii) Reported data should give full details of study methodology, including sampling site, sampling time, how the sample relates to the overall population, and microbiological methods.
(iii) Determination of quantitative data should be encouraged, and, if it becomes available, then full exposure assessments could be developed to investigate mitigation strategies (e.g. use of chlorine in chill water) or to compare alternative practices (e.g. air chilling versus immersion chilling).
(iv) Cross-contamination during processing and handling operations should be studied quantitatively and methodologies for modelling this process should be developed. Cross-contamination during these stages is a critical factor, which is often associated with outbreaks.
(v) At the national level, the collection of consumption data should be promoted. The design of these studies should accommodate the data requirements for exposure assessments. These requirements include population variability, portion size and frequency of consumption.
(vi) In predictive microbiology, the area of survival has been less well studied than growth or death. There are few predictive models that describe survival at chill and frozen temperatures. Further development of these models is essential.