Previous sections examined the data and models available to generate a production-to-consumption risk model. Although there is a substantial amount of literature relating to Salmonella in poultry-rearing operations and during processing, the existing data have severe limitations for usefulness in quantitative (or semi-quantitative) risk assessment. Very few investigations have enumerated Salmonella either on-farm or at processing, or measured how the populations change, for example in a specific stage during processing. Evidence suggests that numbers of Salmonella on poultry carcasses during processing are generally low, at the limits of detection using current enumerative methods, and even then, the commonly used MPN method is very labour and cost intensive. Hence, for practicality, only detect/non-detect (prevalence) investigations are commonly carried out. This results, therefore, in a critical data gap because without enumeration data, risk cannot be estimated. In addition, for both prevalence and the few enumerative investigations, there is a wide diversity in conditions of sampling (sample type, site, size, unit, etc.) and of laboratory testing methods, as well as other confounding factors introduced by the original purposes of the studies and their experimental design. Accommodating these variations and assessing the validity, sensitivity and specificity in each individual report would probably be an exercise in futility. Furthermore, when temporal (if considering data from the early 1980s together with more recent information) and geographical factors are considered, a comprehensive risk model would not be very informative. However, the foregoing sections provide guidelines for the type of information and approach that might be used to develop a production-to-consumption risk model that could be applied to data that represent an individual processing operation, country or region.
Given the lack of use of enumeration data for stages prior to processing, the Exposure Assessment model for purposes of this risk assessment therefore begins at the end of commercial processing, with survey data for contamination levels on chilled broiler carcasses. The subsequent changes in contamination due to storage, handling and preparation were modelled based on information that was presented in detail in the previous section. The construct of the exposure assessment model is summarized in the following model description, and the parameters are shown in Section 6.4
The exposure assessment considered fresh, whole broilers that are purchased at retail, then prepared and consumed in the home. The exposure model was analysed using Monte-Carlo simulation facilitated by @RISK software (ÓPalisade). Each iteration of the model tracks a randomly selected broiler carcass from the time of exit from processing, through storage, preparation and cooking, to consumption. Thus, each run represents a random serving of cooking chicken and the exposures (including cross-contamination) that arise as a result of preparing this serving.
At the start of each iteration, the carcass is assigned to either the Contaminated or Not Contaminated state according to the prevalence of contaminated carcasses. If the carcass is contaminated, the number of Salmonella assumed to be present is selected from the range of values specified by a custom distribution of reported data. If the carcass it is not contaminated, the concentration of organisms is set to zero and this value is held constant for the remainder of the model. For contaminated carcasses, following the start-up step of the model the changes in the level of contamination through storage, preparation (including cross-contamination) and cooking are modelled.
Changes in the level of contamination during the various stages from chilling to consumption occur as a result of a number of variable processes, including storage times and temperatures, practices during preparation, and cooking times and temperatures. This variability is described by probability distributions derived from published and unpublished data and, where necessary, expert opinion.
The model is defined in terms of a number of parameters that describe the processes of broiler carcass distribution and storage, preparation, cooking and consumption. Many of these parameters can be considered general in that they can be used to describe the situation in many countries, such as cooking temperatures and duration of storage. In contrast, some parameters are country specific, such as prevalence of contaminated carcasses exiting processing, and thus to obtain results for individual countries, country-specific data must be input. In addition to the scope for generalization, the model parameters can be modified to determine their influence on the final estimates of exposure.
Prevalence of Salmonella-contaminated carcasses
Prevalence immediately after primary processing was set as a "user" input to the model. In the reports available, prevalence can vary widely from lot to lot, among different processing operations, and among regions and countries, particularly if national standards have been established or Salmonella control programmes operate. Thus, if using this model to describe the situation in a specific country, the likely ranges of local prevalence should be used to generate the risk estimate. Reductions to this value can then demonstrate the effect of prevalence reduction strategies, no matter how they are implemented, on the risk of illness. This would be an important preliminary investigation, prior to determining the best options for reduction, because an idea of the magnitude of the benefit can be realized.
For the purposes of this assessment, a baseline model was first developed, using as the initial input a fixed prevalence level of 20% Salmonella-contaminated carcasses after chilling. The predicted relative change in risk associated with higher or reduced levels of prevalence were modelled for comparison, using fixed values from 1 to 90% contaminated carcasses, and the results compared with the baseline risk estimate.
Numbers of Salmonella on contaminated carcasses
Few studies report on concentrations of Salmonella on broilers. Five studies reporting pathogen numbers at the end of processing (chilling) were summarized in Tables 6.9, 6.10, 6.12 and 6.13 (Surkiewicz et al., 1969; Dougherty, 1974; Lillard, 1980; USDA-FSIS, 1996; Campbell et al., 1983). Since then, data from Canada (CFIA, 2000), shown in Table 6.13, has been made available. All of these studies report MPN values rather than log10 values and all consider immersion chilling.
Some of these studies have characteristics that mean that they are of limited use for inclusion within this exposure assessment. The studies of Surkiewicz et al. (1969) and Campbell et al. (1983) report combined distributions of MPNs from carcasses randomly selected from a number of processing plants. These processing plants differ in their practices relating to the use of chlorine. As chlorine has been reported as having an influence on counts of pathogenic organisms on carcasses (Waldroup et al. 1992), the combined distributions would only be representative if, at a national level, chlorine were used in the same proportion of plants in which it was used in these studies. In addition, these studies are old (published in 1969 and 1983, respectively) and practices affecting concentrations are likely to have changed. Thus, the distributions may not be representative of the current situation. For these reasons, it was decided not to include these studies in the example.
The results reported by Dougherty (1974) and Lillard (1980) give only the mean MPN values, with no information about the distributions of the data. These are therefore of limited use for describing the inherent variability of this parameter. Further, the studies are again old, and may not be representative of current practices. As a consequence, it was decided to exclude them from the example. It is noted that, in the future, more details about unreported original data might be obtainable by contacting the investigators.
National chicken broiler baseline surveys have been conducted in the United States of America in 1994-95 (USDA-FSIS, 1996) and in Canada in 1997-98 (CFIA, 2000) (Table 6.13). These surveys employed statistically based sampling plans, and the same sample collection and laboratory procedures. In the USDA study, carcasses were collected from federally inspected processing plants responsible for approximately 99% of all chickens slaughtered in the United States of America. Similarly, the processing plants from which carcasses were sampled in Canada were federally registered and produced 99.9% of broilers. Both studies report MPN distributions for levels of Salmonella on chilled carcasses.
Although the USDA and CFIA studies are similar in nature, and both reported similar prevalence of Salmonella on chilled carcasses (20% and 21.1%, respectively, by qualitative enrichment of carcass rinse samples), the resulting MPN distributions cannot be combined. This is because practices relating to the use of chlorine differed between the two countries at the time the baseline surveys were conducted. In the United States of America, the addition of chlorine at levels sufficient to maintain 1-5 ppm free chlorine in the overflow was the norm, while in Canada this was not general practice. However, in isolation, the two studies provide good data sets for characterizing the concentration on carcasses after chilling; they are recent, representative and all sampling methods are clearly described. Of course, neither study reports Salmonella concentrations prior to chilling, therefore careful consideration would have to be given if incorporating either data set into a specific processing model.
For the baseline risk model in this assessment, the levels of contamination on chilled broiler carcasses in Canada were used as inputs. This can probably be considered a general data input rather than a country-specific one.
Estimating numbers of Salmonella on contaminated carcasses
Carcass rinses (400 ml) were obtained for 774 broiler carcasses (CFIA, 2000). From each rinse fluid, a sample was tested for the presence or absence of salmonellae using a qualitative enrichment method. Of these, 163 tested positive. Positive rinse fluids were tested by the MPN method, and the MPN per millilitre calculated. The frequency of positive carcasses in five ranges was recorded. These data are shown in Table 6.27. The MPN per carcass was calculated by making two assumptions: first, all organisms on the carcass would be recovered during the shaking procedure, and, second, these organisms would be uniformly distributed within the rinse fluid. Based on these assumptions, the estimated MPN/carcass is equal to 400×MPN/ml (Table 6.28).
Table 6.27. Canadian national baseline data for Salmonella on chicken broiler carcasses
|
Range (MPN/ml) |
Range (MPN/carcass) |
Frequency |
|
<0.03(1) |
<12 |
99 |
|
0.03-0.3 |
12-120 |
60 |
|
0.301-3.0 |
121-1200 |
2 |
|
3.01-30 |
1201-12 000 |
1 |
|
>30.0(2) |
>12 000 |
1 |
NOTES: (1) Positive by qualitative method, negative by quantitative MPN method.
(2) Maximum reported value was 110 MPN/ml. SOURCE: CFIA, 2000.
The distribution for the 163 positive carcasses in Table 6.27 gives a description of the variability in the MPN/carcass. However, as the data is from a sample of carcasses, there will be uncertainty concerning the true variability. The cumulative distribution (Table 6.28) set the minimum value as 1 MPN/carcass and the maximum equal to 110% of the maximum observed MPN, i.e. 110% of 110 MPN/ml = 121 × 400 ml.
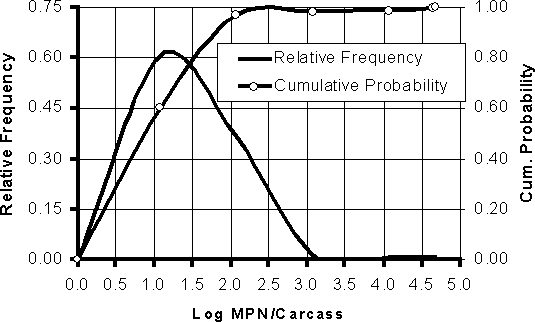
The resulting distribution for log MPN/carcass is shown in Figure 6.9. These distributions were used to characterize the variability in the numbers of Salmonella on contaminated carcasses at the end of processing.
The assumptions concerning the calculation of MPN/carcass from the data reported in the Canadian study require thoughtful consideration. In particular, there is uncertainty and variability relating to the MPN method, which has not been accounted for here. Further, it is likely that the carcass rinse method will not recover all organisms from the carcass. Indeed, it has been reported that on successive carcass rinses of the same bird, aerobic bacteria and enterobacteriaceae can still be recovered after 40 rinses (Lillard 1988, 1989b). These issues should be addressed in future refinements of the exposure assessment.
Table 6.28. Cumulative distribution for carcass concentration, with assumed minimum and maximum concentrations.
|
MPN/carcass |
Log10 MPN/carcass |
Cumulative probability |
|
1 |
0.00 |
0.00 |
|
12 |
1.08 |
0.60 |
|
120 |
2.08 |
0.97 |
|
1200 |
3.08 |
0.98 |
|
12 000 |
4.08 |
0.99 |
|
44 000 |
4.64 |
0.99 |
|
48 400 |
4.68 |
1.00 |
Figure 6.9. Relative frequency and cumulative distribution of Log10MPN/carcass
After processing and packaging, poultry carcasses are distributed to retail stores. It was assumed that between processing plant and retail there would be no change in the prevalence of contaminated carcasses or in numbers of Salmonella on those carcasses. The latter was based on assuming controlled refrigerated transportation conditions (see below for growth at <10°C). Although in the current exercise it was assumed that transportation was well controlled, this needs to be determined on a case-by-case basis. For that reason, a module was created, although not simulated, to illustrate how this step might be potentially modelled and is summarized in Section 6.2.5, together with the other modules.
Three opportunities for Salmonella to multiply on the raw chicken were considered, from the time it enters the retail chain to the point at which the consumer prepares the chicken for cooking. These were (i) during retail storage and display, (ii) in transport from retail to the home, and (iii) during storage in the home. Survival and growth models currently available for estimating population changes during these stages were reviewed in Section 6.2.5. There are no suitable models to estimate survival and die-off for salmonellae in or on broilers, and therefore for the purposes of this risk assessment it was assumed that the salmonellae either grow given suitable conditions, or the population remains static on poultry, but does not decrease.
Several growth models for salmonellae were evaluated for their relevance and ‘ease of use’ for this assessment. The growth model selected was developed by Oscar (1999b) for S. Typhimurium (Equation 6.9).
|
|
Equation 6.9 |
The equation parameters were developed using ground chicken breast meat as the growth medium (rather than laboratory media), and the model has a wider growth temperature range than others (10°C-40°C). The author also validated the model satisfactorily. The growth model takes account of the influences of temperature and salt concentration (including any previous exposure to NaCl, as in the case of pre-culturing inocula in the laboratory) on the growth of S. Typhimurium. The author’s opinion was sought on the likely water activity of broiler meat used in the development of the model and a value of 0.99 or 1.9% salt was advised. Therefore, the salt concentration parameters were both fixed at 1.9%, and the external temperature remained a variable that determined the growth rate. A final assumption was that there was no lag phase in the growth phases modelled. This is reasonable given that salmonellae on or in broiler meat would have had ample time to adapt to their environmental conditions prior to retail delivery, and it would be unlikely that the cells would experience significant lag time before commencing growth once storage temperatures rose. It has been emphasized elsewhere that predictive models can only be used for interpolation within their boundaries. The growth model has a lower temperature bound of 10°C and hence it was assumed that there was no growth below this. The upper temperature bound (40°C) was assumed not to be exceeded under normal storage conditions. The lower temperature bound assumption may underestimate some growth at <10°C.
Section 6.2.5 of the Exposure Assessment discussed the modelling of non-isothermal temperature profiles. It was noted that time-temperature storage (retail display, home, etc.) profiles are generally not available for raw poultry. Therefore, in this assessment, the observations of Ross (1999) were used, namely that microbial growth during isothermal temperature conditions could be reasonably predicted using the average temperature of the isothermal profile. Hence, any growth of salmonellae in broilers during storage was based on distributions around the reported average storage temperatures.
Note that while the growth model can be considered general, the time and temperature profiles used within it must be country specific.
Retail storage
A study in the United States of America (Audits International, 1999) reported survey data on the variability of average retail storage temperatures. These may or may not reflect similar conditions in other countries, but in the model these values can be readily replaced with other, more representative, temperatures if appropriate. Temperatures were recorded for 975 fresh meat products. The overall average temperature recorded was 4°C with a standard deviation of 2.8°C. The maximum temperature reported was 10°C and the minimum was -7.2°C. For this exposure assessment model, the variability in retail storage temperatures was represented by a truncated Normal distribution using these data. Hence, during the simulation, values could not be selected which were above the maximum or below the minimum recorded temperatures. Therefore, as 10°C represents the lower temperature bound of the growth model, growth was achieved only when an average retail storage temperature of 10°C or above was selected at random during the Monte Carlo simulation.
The growth model calculated a specific growth rate for S. Typhimurium at the average storage temperature. The extent of growth was determined by the length of storage time. Advice from retailers in Ireland was sought to estimate the minimum and maximum length of time that fresh chicken broilers were kept at retail. It would be preferable to obtain this information in a much more structured manner, or through a commissioned study, but, as a first step, this may be appropriate. The minimum value was estimated as 2 days and the maximum as 7 days. It was assumed that all values were equally likely and therefore the retail storage duration was represented by a uniform distribution. However, a correlation factor of -0.75% was used to ensure that, in the simulation, combinations of high storage temperatures and long storage times were unlikely (resulting in detectable spoilage and the product discarded before consumption, as would be the case in reality). The specific growth rate calculated by the growth model was multiplied by the storage time in days to give a value for the log10 increase in numbers of salmonellae.
Transport from retail to home
Data describing the variability of temperatures for foods during transport from the retail store to the home have been collected in the United States of America (Audits International, 1999). Variability in transport times from store to home was also measured during this study.
Given the parameters of the growth model used in this assessment, a product temperature of 10°C must be exceeded before a specific growth rate is calculated for Salmonella. Therefore it was assumed that if the external temperature that was experienced during transport to the home were below 10°C, no growth would occur. Hence, an estimate of the external temperature during transport was important to determine microbial growth. For the purposes of this assessment, typical northern European temperatures were applied, with the temperature variability represented using a PERT distribution centred on the most likely temperature value. These were a minimum of 0°C, a maximum of 24°C, and with a most likely value of 13°C.
The United States of America study reported changes in product temperature during transport from the retail store to the home for 975 fresh meat products. The overall average was 3.72°C with a standard deviation of 2.82°C. The maximum temperature change was defined as the difference between the external (ambient) air temperature and the minimum growth temperature of the model (10°C). The minimum temperature change was taken as 0°C (no change). This variability was represented by a truncated Normal distribution in a similar way to that described previously for retail storage.
The maximum product temperature during transport was calculated as the retail temperature of the product plus the temperature change if any change occurred. The average product temperature was calculated as the mean of the maximum product temperature plus the retail product temperature. This average temperature was used to calculate the specific growth rate for salmonellae in the growth model.
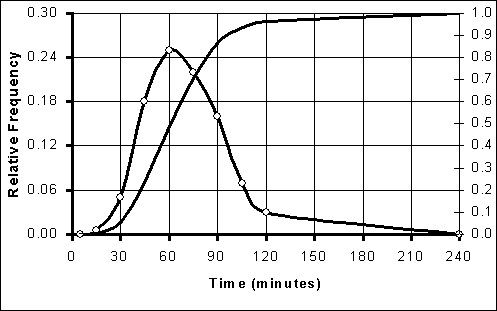
The data for transport time were reported as the frequency of measurements in 15-minute time intervals. A cumulative distribution was fitted to these values and used to represent the variability in these data (Table 6.29 and Figure 6.10). The increase in log10 numbers of salmonellae in or on a simulated broiler was calculated by multiplying the specific growth rate by the transport time.
Table 6.29. Transportation time from retail to home.
|
Time (minutes) |
Frequency |
Cumulative |
|
- |
0.000 |
0.000 |
|
15 |
0.005 |
0.005 |
|
30 |
0.050 |
0.055 |
|
45 |
0.180 |
0.235 |
|
60 |
0.250 |
0.485 |
|
75 |
0.220 |
0.705 |
|
90 |
0.160 |
0.865 |
|
105 |
0.070 |
0.935 |
|
120 |
0.030 |
0.965 |
|
240 |
0.035 |
1.000 |
SOURCE: Data from Audits International, 1999.
Figure 6.10. Probability distribution for transportation time from retail to home.
Home storage
Data on the variability of product temperatures during domestic refrigerated storage are available for the United States of America (Audits International, 1999). Temperatures during domestic refrigerated storage were recorded for unspecified food products, being chilled at an average of 4°C with a standard deviation of 2.65°C, with a maximum temperature of 21.1°C and a minimum of -6.1°C. The variability of reported home storage temperatures was represented by a truncated Normal distribution using these temperatures. Values could not be selected during the simulation above the maximum or below the minimum temperatures recorded. Again, because 10°C represented the lower temperature bound of the growth model, pathogen growth occurred only when a home storage temperature of 10°C or above was randomly selected during the Monte Carlo simulation.
The specific growth rates for S. Typhimurium were calculated for the average home storage temperatures and the extent of growth was determined by the length of storage time in the home. Based on adherence to the "use-by" date, expert opinion estimated the minimum value would be no storage time (immediate use), the maximum would be 5 days, with a most likely value of 2 days in the refrigerator. The variability in storage time was represented with a PERT distribution centred on the most likely value of 2 days. A correlation factor of -0.75% was used to ensure that combinations of high temperature and long storage time were unlikely (detectable spoilage and discard of product). The specific growth rate calculated by the growth model was multiplied by the storage time to give a value for the log10 increase in numbers of salmonellae.
Cross-contamination
Cross-contamination of foods during the handling and preparation of raw meats is a recognized hazard in the home. If this parameter were ignored in a risk assessment model, it is likely that the risk would be underestimated. To estimate the risk of illness attributable to the cross-contamination of other foods during preparation of raw poultry, it is necessary to have information about the likelihood that cross-contamination will occur, and what is the likely number of bacteria transferred from raw to a ready-to-eat food. Section 6.2.6 described investigations that have studied these aspects. Estimates of the probability of cross-contamination were available from observational studies of food preparation behaviours (Worsfold and Griffith, 1997b). Estimates for the proportion of bacteria transferred from a raw food to hands or cutting board, and subsequently to other foods, were obtained from studies by Zhao et al. (1998). For the present risk assessment, two pathways of potential cross-contamination were modelled: from raw poultry via hands, and from raw poultry to cutting boards to other foods.
The probability of a person not washing their hands after handling raw poultry was estimated to be 0.6 (Worsfold and Griffith, 1997b). The proportion of salmonellae transferred from the raw broiler to the hands was estimated to be 10% (Zhao et al., 1998). It was assumed that if salmonellae were present, the number of salmonellae on the broiler and the proportion transferred would determine the numbers transferred. If hands were then washed, no further cross-contamination occurred. Hand washing was described by a Binomial distribution with a probability based on the values returned from the uncertainty model, as described previously. Based on this, if the model returned that hands were not washed, then salmonellae would be transferred to other foods. The numbers of salmonellae contaminating the other food was then calculated to be a function of the number of organisms on the hands and the proportion transferred.
Cross-contamination via cutting boards was simulated in the same way as cross-contamination from hands. However, here the probability estimate for the board being used for other food was 0.6 (Worsfold and Griffith, 1997b).
Cooking module
Preparing the food for consumption was modelled following an approach described by Fazil et al. (unpublished) and A.M. Fazil (personal communication) in a risk assessment for Campylobacter in poultry. Briefly, adequate cooking will destroy salmonellae and therefore it is only the broilers that are inadequately cooked that may still contain salmonellae at time of consumption (for the purposes of this module alone, post-cooking contamination is not considered). However, even with undercooking, it was assumed that salmonellae present on the external surfaces of the carcass will be inactivated, and that only some proportion of the total number - those more protected from heat penetration -would survive. The survival of the ‘protected’ bacteria will then depend on their heat resistance, and the length of time at some final temperature. The work of Fazil et al. (unpublished) and A.M. Fazil (personal communication) modelled this scenario based on published data for thermal profiles during cooking and on expert opinion, which were included in the example model for Salmonella in broilers.
The input variables in this module are sources of uncertainty in the example model. Table 6.30 shows the variables and their associated probabilities (Fazil et al., unpublished; A.M. Fazil, personal communication).
Table 6.30. Variables used to describe cooking of broilers.
|
Variable |
Probabilities |
||
|
Minimum |
Most Likely |
Maximum |
|
|
Proportion of broilers not adequately cooked |
0.05 |
0.1 |
0.15 |
|
Proportion of salmonellae in protected areas |
0.1 |
0.16 |
0.2 |
|
Temperature exposure of protected bacteria (°C) |
60 |
64 |
65 |
|
Time exposure of protected bacteria (minutes) |
0.5 |
1 |
1.5 |
SOURCE: Fazil et al., unpublished.
The probability that a randomly selected broiler would be undercooked was determined by a Binomial distribution. If the simulation determined that the broiler was adequately cooked, the broiler was considered Salmonella-negative. If the simulation determined that the broiler was inadequately cooked, then the number of salmonellae surviving was calculated as described previously in this section. Having determined the number of salmonellae in protected areas and the time and temperature they may experience, a D-value was used to calculate the numbers of salmonellae surviving. The D-value applied was dependent on temperature and was developed and described in Equation 6.5 (see Section 6.2.6).
Consumption
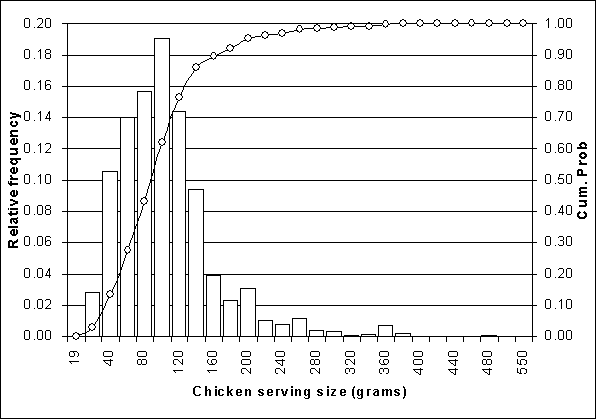
Section 6.2.7 discussed the consumption data requirements for microbial risk assessment. For the purposes of this assessment, consumption data collected in Ireland by IUNA were used to estimate the range of amounts of chicken in a single serving that might be consumed by individuals 18 to 64 years of age. Note, however, that use of this model in a national setting will require country-specific data to be used. These data are shown as frequency and cumulative distributions in Figure 6.11. The amounts consumed were for meals consisting of whole portions of chicken meat; recipes in which the chicken was present as an ingredient were not considered. For chicken on the bone, the intake was calculated by correcting the weight to reflect the edible portion. The consumption database showed that over the 7 days of recording for 1379 subjects, 65.5% of subjects (903) consumed chicken on 1695 eating occasions. For the purposes of this assessment, the risk estimations were based on one serving of chicken every two weeks (specifically as whole portions, prepared from fresh whole carcasses in the home).
The cumulative frequency distribution was used during simulation to randomly generate serving weights for broiler meat. A United Kingdom retailer supplied data on the likely weights of broilers. Minimum weight was estimated to be 1.1 kg, maximum weight was estimated to be 2.5 kg, with a most likely value of 1.5 kg. These data were fitted with a PERT distribution, which was used during the simulation to randomly generate a broiler weight. Expert opinion from a United Kingdom producer estimated that 30% of the weight of a chicken was edible meat. Therefore the broiler weight was reduced by 70% to generate an edible meat weight. Finally, the edible meat weight was divided by the serving size to calculate the number of servings per broiler.
Figure 6.11. Frequency distribution for the consumption of chicken meat per eating occasion.
The outcomes of exposure assessment are probability of ingestion and number of salmonellae ingested in a serving. The number of organisms ingested from undercooked poultry was calculated by dividing the number of organisms on a broiler by the number of servings from the broiler. The ingestion of Salmonella from raw poultry via a cross-contamination event was treated as a separate pathway with a separate risk estimate. By running the model through Monte Carlo simulation, distributions were generated of the number of salmonellae that a consumer might be exposed to per serving of cooked broiler meat, and per cross-contamination exposure event.