Se llama cohorte o clase anual o incluso generación, a un grupo de peces de un stock nacidos en el mismo año. El siguiente esquema ilustra las diferentes fases del ciclo vital de una cohorte:
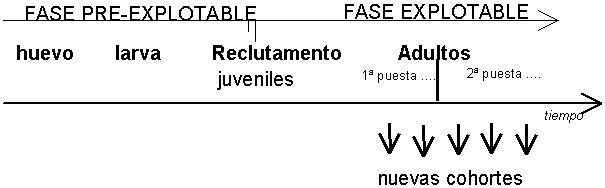
Figura 3.1 Ciclo vital de una cohorte
Empezando, por ejemplo, por la fase huevo. Las fases siguientes serán larva, juvenil y adulto.
Al número de individuos de una cohorte que entran por primera vez en el área de pesca se le llama reclutamiento a la pesca o a la fase explotable. Estos individuos crecen, desovan (una o varias veces) y mueren.
A partir de la 1ª puesta los individuos de la cohorte pasan a ser adultos, y, en general, desovan nuevamente todos los años dando origen a nuevas cohortes.
Las fases de la vida de cada cohorte previas al reclutamiento al área de pesca (huevo, larva, pre-reclutas), son fases importantes de su ciclo vital pero, generalmente, no están sujetas a explotación, de tal modo, que las variaciones en su abundancia se deben fundamentalmente a factores ambientales (viento, corrientes, temperatura, salinidad, ...). La mortalidad en estas fases no explotables suele ser muy elevada particularmente en la última parte de la fase larvaria (Cushing, 1996) por lo cual la supervivencia hasta el reclutamiento es muy baja. Esta mortalidad, como ya se ha indicado, no se debe a la pesca.
El reclutamiento a la fase explotable de una cohorte (número de individuos que entran por primera vez en la fase explotable en un año determinado), puede producirse a lo largo de varios meses de la forma que se muestra en los siguientes esquemas:

Figura 3.2 Reclutamiento a la fase explotable
Exceptuando algunos casos, las formas de reclutamiento se pueden simplificar suponiendo que todos los individuos se reclutan en un instante, tr, que será la edad de reclutamiento a la fase explotable. Por acuerdo se considera que el reclutamiento tiene lugar el día 1 de enero (inicio del año civil en muchos países). La simplificación y el acuerdo mencionados anteriormente no alteran mucho los resultados de los análisis, y en cambio los simplifican además de ajustarse a los períodos a que se refieren las estadísticas comerciales.
Se debe tener en cuenta en todo momento, que la 1ª puesta no tiene lugar a la misma edad para todos los individuos de la cohorte. La proporción de individuos que desovan por 1ª vez aumentan con la edad, desde cero hasta el 100%. A partir de la edad en que el 100% han desovado por 1ª vez, todos los individuos serán adultos. El histograma o la curva que representan estas proporciones son conocidas como ojiva de madurez.
En algunos casos, también se puede simplificar la ojiva de madurez suponiendo que la 1ª puesta se produce a la edad tmat o edad de 1ª madurez. Esta simplificación significa que los individuos de edad inferior a tmat son considerados juveniles y los de edad igual o superior son considerados adultos.
La Figura 3.3 representa una ojiva de madurez en forma de histograma o de curva:

Figura 3.3 Ojiva de madurez
Sea el intervalo (ti, ti+1) de tamaño Ti = ti+1 - ti de la evolución de una cohorte en el tiempo y Nt el número de supervivientes de la cohorte en el instante t del intervalo Ti (ver Figura 3.4).
La información existente sugiere que las tasas medias de variación porcentual de Nt pueden considerarse aproximadamente constantes, i.e., tmr (Nt) » constante.
Suposición básica
La tasa instantánea relativa de variación de Nt, en el intervalo Ti es:
tir (Nt) = constante negativa = - Zi
|
|
Ni = no de supervivientes al INICIO del intervalo (ti, ti +1) Ni+1 = no de supervivientes al FINAL del intervalo (ti, ti +1) |
Figura 3.4 Evolución de Ni en el intervalo Ti
El modelo de la evolución de Nt, en el intervalo Ti, es un modelo exponencial (porque tir(Nt) es constante). Este modelo tiene las siguientes propiedades:
Propiedades
1. Expresión general. Partiendo de la asunción básica
tir(Nt) = -Zi
y dado que la condición inicial que para t = ti también Nt = Ni entonces:
2. Número de supervivientes, Ni+1, al final del intervalo Ti
3. Número de muertos, Di, durante el intervalo Ti
(nótese que Di es positivo, en cambio la variación DNi = Ni+1- Ni es negativa)
4. Número acumulado de supervivientes, Ncumi, durante el intervalo Ti
5. Valor central aproximado, Ncentrali, en el intervalo Ti
6. Número medio,
 , de supervivientes durante
el intervalo Ti
, de supervivientes durante
el intervalo Ti
(Ricker)
cuando
es pequeño (Zi.Ti < 1)
Comentarios
1. La suposición básica, a veces, es presentada en términos de tasas instantáneas absolutas, o sea,
tia (lnNt) = -Zi o
tia (Nt) = - Zi.Nt { tia (Nt) proporcional a Nt}
Zi = coeficiente de mortalidad total, supuestamente constante en el intervalo Ti
Nótese que:
+Zi = tir de mortalidad total de Nt
–Zi = tir de variación de Nt
2. Unidad de Zi
De la definición se deduce que Zi se expresa en unidades de [tiempo]-1. Por convención se adopta la unidad «año-1» tanto cuando se aplica a un intervalo de tiempo inferior como superior a un año.
Las expresiones siguientes muestran de una forma simplificada el cálculo de la unidad de Zi, con las reglas y símbolos [.] de dimensión habituales en la determinación de unidades físicas.
donde
3. Tasa anual de supervivencia, Si
Cuando Ti = 1 año, será:
y también
Si = tasa anual de supervivencia en el año i
(o % del número inicial de individuos que sobrevive al final del año).
1 - Si = tasa anual de mortalidad en el año i
Por definición es el % del número inicial que muere durante el año, o sea, la tasa media relativa tmr (Nt) de mortalidad de Nt, durante un año, en relación al número inicial, Ni
4. Tasa media absoluta

5. Tasa media relativa
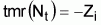 en relación a
en relación a
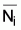
6. Nótese que Si tiene que estar comprendida entre 0 y 1, o sea,
0 £ Si £ 1 además Zi puede ser > 1
Si los límites del intervalo Ti fuesen (ti, ¥) entonces seria:
Ti = ¥
Ni+1 = 0
Di = Ni
y
Las causas de muerte debidas a la pesca se distinguirán de las restantes causas de muerte de los individuos de la cohorte. Estas últimas se agruparan en una única causa llamada mortalidad natural. Así, a partir de las propiedades del modelo exponencial
tir(Nt) total = tir(Nt) natural + tir(Nt) pesca
Considerando el intervalo Ti y suponiendo que, en ese intervalo, las tasas instantáneas de mortalidad debidas a causas naturales y a la pesca son constantes y iguales a Mi y a Fi, respectivamente, será
Zi = Fi + Mi
Multiplicando ambos miembros de la igualdad anterior por
 :
:
como 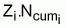 es
el número, Di, de muertos a causa de la mortalidad
total, entonces,
es
el número, Di, de muertos a causa de la mortalidad
total, entonces,
De modo semejante
 será el
número de individuos muertos a causa de la pesca, o sea, la Captura,
Ci, en número y, por tanto,
será el
número de individuos muertos a causa de la pesca, o sea, la Captura,
Ci, en número y, por tanto,
Nótese que también,
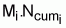 será el
número de individuos muertos debido a causas naturales.
será el
número de individuos muertos debido a causas naturales.
La tasa de explotación, Ei, durante el intervalo Ti fue definida por Beverton y Holt (1956) como:

La captura en número, Ci, en el intervalo Ti, puede expresarse de diferente modo:
Ci = Fi. Ncumi
Comentarios
1. Ricker (1975) define la tasa de explotación, Ei*, como el porcentaje del número inicial que es capturado en el intervalo Ti, o sea, Ei* = Ci / Ni.
a) La definición de Ricker puede ser más natural pero, matemáticamente, la definición de Beverton & Holt es más útil
b) Es fácil de verificar que
2. La tasa de explotación, Ei, no tiene unidades, es un número abstracto.
3. Los valores posibles de Ei están comprendidos entre 0 y 1, siendo 0 cuando no hay explotación y 1 cuando la captura Ci es igual al número de muertos Di, o sea, cuando Mi = 0.
Para estudiar la evolución de la biomasa de una cohorte, se puede utilizar el modelo de la evolución de una cohorte, en número, y combinarlo con un modelo de la evolución del peso medio de un individuo de la cohorte. En efecto, la biomasa Bt es igual a Nt.Wt donde Wt es el peso medio individual en el instante t. Por otro lado, también hay un interés, más general, en disponer de un modelo para la evolución del peso individual, Wt, y de un modelo para la evolución de la talla individual, Lt.
Para definir un modelo para el crecimiento en peso individual, Wt, hay varias alternativas:
ALTERNATIVA 1:
A) Se define un modelo para el crecimiento individual medio en talla, Lt
B) Se define la relación Talla-Peso.
C) Se combina A) con B) y se obtiene un modelo para el crecimiento individual medio en peso, Wt
ALTERNATIVA 2:
D) Se define un modelo directamente para Wt y Lt.
ALTERNATIVA 1
A) Modelo para el crecimiento individual en talla
Los modelos para ser usados en biología pesquera serán válidos para la fase explotable del recurso. El más conocido es el Modelo de von Bertalanffy (1938). Las observaciones existentes sugieren que hay una talla asintótica, i.e., que hay una talla a la cual tiende la talla individual.
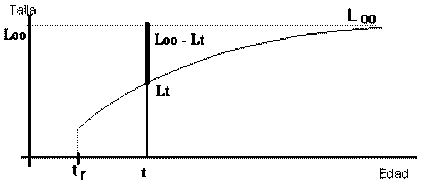
Figura 3.5 Modelo de von Bertalanffy
t – edad
Lt – talla media individual a la edad t
L¥– talla asintótica
tr – inicio de la fase explotable
Así, Lt presenta una evolución donde se puede verificar que:
La tia(Lt) no es constante (porque el crecimiento no es lineal)
La tir(Lt) no es constante (porque el crecimiento no es exponencial)
Se observa, no obstante, que la variación de la magnitud (L¥- Lt) (a la que se podría llamar «lo que falta por crecer»), presenta una tasa relativa constante y podrá ser descrita por un modelo exponencial. Así, se puede adoptar la:
Suposición básica
tir (L¥- Lt) = - K = constante negativa durante toda la vida explotada
en que K es el coeficiente de crecimiento (atención: el coeficiente de crecimiento K no es la velocidad de crecimiento sino la velocidad relativa de lo que «falta» por crecer!!).
Las propiedades de este modelo (ya que es un modelo exponencial) pueden ser obtenidas directamente de las propiedades generales del modelo exponencial con la condición inicial:
Propiedades del modelo de crecimiento individual en talla de Beverton & Holt (1957) deducidas a partir del modelo exponencial de(L¥- Lt).
|
Propiedades del modelo exponencial para (L¥- Lt) |
Modelo de von Bertalanffy para Lt |
||
|---|---|---|---|
|
1. |
Expresión general |
||
|
|
|
||
|
Parámetros L¥= talla asintótica K = coeficiente de crecimiento
|
Parámetros L¥= talla asintótica K = coeficiente de crecimiento
|
||
| |
para ta = t0 y La = 0: |
para ta = t0 y La = 0: |
|
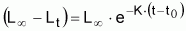 |
|
||
| 2. |
Valor al final del intervalo Ti
|
||
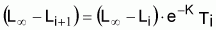 |
expresión Ford-Walford (1933–1946) |
||
| 3. |
Variación durante el intervalo Ti
|
||
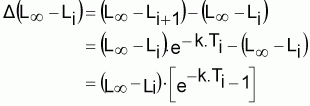 |
será:
|
||
| 4. |
Valor acumulado durante el intervalo Ti
|
||
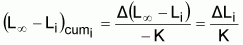 |
visto que:
|
||
| 5. |
Valor medio durante el intervalo Ti
|
||
 |
expresión de Gulland y Holt (1959) visto que: |
||
| 6. |
Valor central del intervalo Ti
|
||
|
|
e |
||
B) Relación Talla-Peso
Es común utilizar la función potencia para relacionar el peso individual con la talla total (o cualquier otra). Así:
donde la constante a es llamada factor de condición o índice ponderal y la constante b constante de morfismo. Esta relación puede justificarse aceptando que, grosso modo, «el porcentaje de crecimiento en peso» es proporcional «al porcentaje de crecimiento en talla» (de otro modo el individuo devendría «desproporcionado») y, por tanto, adoptando la suposición básica:
donde b es la constante de proporcionalidad.
|
C) Combinación de A) y B) y comentarios: |
|
|---|---|
|
1. |
El resultado de la combinación de
Esta relación de crecimiento en peso es conocida como ecuación de Richards (1959). Cuando b=3 la ecuación es la ecuación de crecimiento de von Bertalanffy (1938). |
|
2. |
De |
|
3. |
Sea Como
tenemos
En la práctica se usa
|
|
4. |
Los modelos de Richards y de von Bertalanffy no son los
únicos modelos usados para la evolución de
|
|
5. |
Históricamente, el modelo de von Bertalanffy fue desarrollado a partir de la suposición básica
Donde Cte1 y Cte2 fueron llamadas por von Bertalanffy, constante de anabolismo y de catabolismo, respectivamente. Adoptando la relación
(donde Cte1 y Cte2 son otras constantes). Ecuación diferencial cuya solución da la ecuación de von Bertalanffy |
ALTERNATIVA 2
D) Modelo para Wt y Lt directamente
En la alternativa 1, se desarrollo un modelo para el crecimiento en talla, y a continuación se construyó el modelo para el crecimiento en peso, usando la relación entre el peso y la talla.
La suposición básica adoptada por la alternativa
1 utilizó la característica
 en lugar del peso con el
fin de poder tener una característica cuya tir fuese constante, i.e., un
modelo exponencial, y consideró la relación W=a.Lb para
derivar el modelo de crecimiento en peso. Nótese que se puede decir que L
fue considerada como una función de W, esto es, L= (W/a)1/b.
Por tanto, en vez de esta función de W, se puede utilizar otra
función del peso H(Wt), de tal modo que se pueda formular
directamente la suposición básica:
en lugar del peso con el
fin de poder tener una característica cuya tir fuese constante, i.e., un
modelo exponencial, y consideró la relación W=a.Lb para
derivar el modelo de crecimiento en peso. Nótese que se puede decir que L
fue considerada como una función de W, esto es, L= (W/a)1/b.
Por tanto, en vez de esta función de W, se puede utilizar otra
función del peso H(Wt), de tal modo que se pueda formular
directamente la suposición básica:
con la condición inicial
Propiedades
Las propiedades de este modelo (ya que es un modelo exponencial) pueden obtenerse directamente de las propiedades generales del modelo exponencial. Resulta particularmente interesante derivar la expresión general para Wt resultante de diferentes opciones da la función H.
|
1. |
Expresión general |
|
|
|
o |
|
|
2a. |
Ecuación de Richards en peso |
Adoptada la función H(Wt) = Wt1/b De la expresión general se deduce: |
|
|
|
|
|
|
La ecuación de Richards, cuando b=3, es la ecuación de von Bertalanffy, así: |
|
|
2b. |
La ecuación de von Bertalanffy, en peso, será: |
|
|
3. |
Ecuación de Gompertz en peso |
Adoptando la función H(Wt) = ln Wt De la expresión general se deduce:
|
|
4. |
Las respectivas ecuaciones con la talla podrán ser obtenidas adoptando otras funciones de H(Wt). Así: |
|
|
4a. |
Ecuación de von Bertalanffy, con la talla |
Se adopta H(Wt) = Lt y devendrá: Lt = L¥- (L¥-La).e-K.(t-ta) |
|
4b. |
Ecuación de Gompertz, con la talla |
Se adopta H(Wt) = ln Lt y devendrá:
|
|
5. |
Ecuaciones simplificadas Las ecuaciones de crecimiento individual, tanto en talla como en peso, se simplifican cuando se selecciona H(Wa) = 0 para ta = t* |
|
|
|
Así la expresión general se reduce a: |
|
|
5a. |
La ecuación de Richards, con el peso, simplificada será: |
|
|
|
donde t* es t0 en consecuencia H(Wa) = 0 en el modelo de Richards significa que también Wa será cero. |
|
|
5b. |
La ecuación de Gompertz, en peso, simplificada será: |
En este caso H(Wa) = 0 corresponde a Wa = 1 |
|
5c. |
La ecuación de Richards, con la talla, simplificada será: |
(con La = 0 para ta = t0) |
|
5d. |
La ecuación de Gompertz, con la talla, simplificada será: |
(con La = 1 para ta = t*) |
Comentarios
1. La ecuación de Gompertz, con el peso, es semejante a la ecuación de Gompertz, con la talla, pero en sus formas simplificadas t* son edades diferentes, por lo cual corresponderán respectivamente a Wa = 1 y a La = 1.
2. La ecuación de Gompertz con la talla es semejante a la de von Bertalanffy con Lt substituida por ln Lt. En la práctica este hecho permite utilizar los mismos métodos particulares de estimación de parámetros en ambas ecuaciones, usando L en la expresión de von Bertalanffy y lnL en la expresión de Gompertz. (Ver Sección 7.4)
3. Se llama de nuevo la atención acerca de que, en la
práctica, se usan Lcentrali y Wcentrali en vez de
los valores medios, 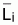 y
y
 .
.
4. La curva de crecimiento en talla de Gompertz inflexiona en el punto (tinfl, Linfl):
tinfl = ta+(1/K).ln(ln(L¥/La))
Linfl = L¥/ e
5. La curva de crecimiento en peso de Gompertz inflexiona en el punto (tinfl, Winfl):
tinfl = ta+(1/K).ln(ln(W¥/Wa))
Winfl = W¥/ e
6. La curva de crecimiento en talla de Richards no tiene punto de inflexión, no obstante la curva de crecimiento en peso tiene inflexión en el punto (tinfl, Winfl):
En el caso particular de la ecuación de von Bertalanffy será:
Winfl = (8/27).W¥
y
tinfl = t0+(1/k).ln3
7. Algunos autores aplican la ecuación de Gompertz usando como parámetros ta y Wa el punto de inflexión tinfl y el peso asintótico W¥.
Por tanto será
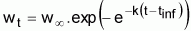 o
o
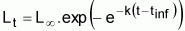
A veces la expresión es presentada en la forma general

Entonces, los parámetros del modelo serán: L¥= a; k = -c e tinfl = (1/c).ln(-b)
8. En acuicultura, donde el estudio del crecimiento incluye edades muy jóvenes y se produce igualmente una inflexión en el crecimiento en talla, es costumbre utilizar la ecuación de Gompertz. En la pesca, la tradición es usar la ecuación de von Bertalanffy.
9. Un modelo, que a veces puede ser útil, es el modelo de Ricker (1975). Este modelo es válido para un intervalo de tiempo dado Ti y no necesariamente para toda la vida explotable del recurso pesquero. En efecto, el modelo se basa en la suposición básica de que el crecimiento individual es exponencial en el intervalo Ti.
Así, por ejemplo, será,
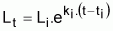
donde ki puede ser diferente de un intervalo a otro.
1. Biomasas
Teóricamente, se podría decir que la biomasa en el instante t del intervalo Ti viene dada como:
Bt = Nt. Wt
y, por tanto, la biomasa acumulada en el intervalo Ti seria:
y la biomasa media en el intervalo Ti seria:
También el peso medio de la cohorte,
 , en el intervalo
Ti seria:
, en el intervalo
Ti seria:
Y, por tanto, dividiendo ambos términos de la
fracción por Ti será
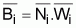
2. Captura, en peso
La captura en peso, Yi, durante el intervalo T se expresara como el producto de la captura, Ci, por el peso medio individual durante el intervalo Ti:
Comentarios
En la práctica se considera que
 es aproximadamente igual a
es aproximadamente igual a
 en el intervalo
Ti.
en el intervalo
Ti.
La expresión anterior de Yi también podrá expresarse como:
Se considera la evolución de una cohorte durante toda la vida explotable, con inicio a la edad tr. Se consideran intervalos, Ti, de tiempo, donde i varía desde el primer intervalo hasta el último, cubriendo toda la fase explotable (los intervalos acostumbran a ser de 1 año...).
La Figura 3.6 simula la evolución del número de supervivientes de la cohorte, N, y la evolución de las capturas en número, C, que se van obteniendo durante los sucesivos intervalos de tempo Ti.
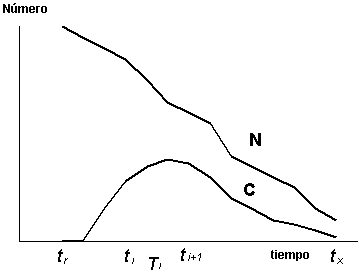
Figura 3.6 Evolución del número de supervivientes de la cohorte, N, y de las capturas en número, C
La Figura 3.7 simula la evolución de la biomasa de la cohorte, B, y la evolución de las capturas en peso, Y, que se van obteniendo durante los sucesivos intervalos de tiempo Ti.
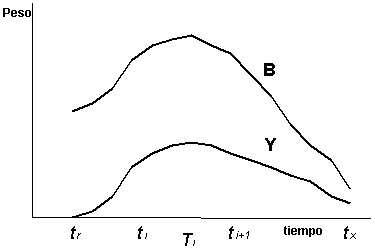
Figura 3.7 Evolución de la biomasa de la cohorte, B, y de las capturas en peso, Y
Valores de las características más importantes de la cohorte, durante todo la fase explotable
|
Duración de la vida de la cohorte |
l= S Ti |
|
Número total de muertos |
D = S Di (= R (reclutamiento) cuando mueren todos los individuos) |
|
Número acumulado de supervivientes |
|
|
Número medio de supervivientes |
|
|
Biomasa acumulada de supervivientes |
|
|
Biomasa media de supervivientes |
|
|
Captura en número |
C = S Ci |
|
Captura en peso |
Y = S Yi |
|
Peso medio de la cohorte |
|
|
Peso medio en la captura |
Wcapt = Y / C |
|
Edad crítica |
tcrítica = edad en que B es máxima, cuando la cohorte no es explotada. |
Comentarios
1. A primera vista puede parecer que los valores de las características de una cohorte durante toda la fase explotable no tienen gran interés, porque, en la práctica, la pesca raramente se ejerce sobre una cohorte aislada. En todo momento están presentes y disponibles para la pesca, simultáneamente, los supervivientes de varias cohortes.
2. A pesar de esto y por razones que se verán más adelante, es importante analizar las características de una cohorte durante toda su vida explotable. El conocimiento acerca de la evolución de una cohorte, en número y en biomasa, particularmente a la edad crítica, tiene gran importancia para el éxito de la acuicultura. Como Bt = Nt. Wt la edad crítica, tcrítica, será la edad t en el intervalo Ti donde
tir (Wt) = - tir(Nt)=M por consiguiente, siendo la edad crítica correspondiente la biomasa máxima no explotada, la derivada de B con respecto a t será igual a cero.
Nótese que Ncum puede expresarse en función del reclutamiento como
Ncum = R.{...}
donde {...} representa una función de los parámetros biológicos y de los coeficientes de mortalidad Fi durante los años de la vida de la cohorte. También Bcum puede expresarse como:
Bcum = R.{...}
donde {...} tiene el mismo significado incluyendo los parámetros de crecimiento.
Beverton y Holt (1957) deducen expresiones algebraicas para las características de una cohorte durante la vida explotada adoptando algunas suposiciones simples:
1. La fase explotada de la cohorte se inicia a la edad
 y se extiende hasta el
infinito.
y se extiende hasta el
infinito.
2. El coeficiente de mortalidad natural, M, es constante durante toda la fase explotable.
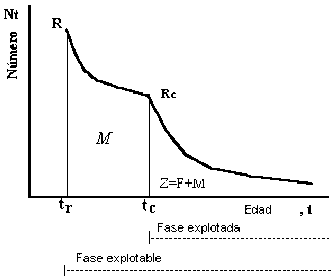
Figura 3.8 Vida de una cohorte durante la fase explotable
3. El coeficiente de mortalidad por pesca, F, es constante durante toda la fase explotada, esto es, la fase de la vida de la cohorte que se inicia en tc.
4. El crecimiento se ajusta a la ecuación de von Bertalanffy con La = 0 para ta = t0
Ecuaciones básicas referentes a la fase explotada
|
1. |
c (cociente entre la talla a la edad
|
|
|
2. |
Reclutamiento |
|
|
3. |
Número acumulado |
|
|
4. |
Captura en número |
|
|
5. |
Biomasa acumulada
|
|
|
|
de forma simbólica se escribir simplemente
|
|
|
6. |
Peso medio en la captura |
|
|
7. |
Captura en peso |
|
|
8. |
Edad media en la captura |
|
|
9. |
Talla media en la captura |
|
|
10. |
Edad crítica |
|
Comentarios
1. La simplificación de Beverton y Holt permite calcular cualquier característica de la cohorte durante su vida con expresiones algebraicas sin necesidad de tener que sumar los valores de la característica en los sucesivos intervalos Ti. Este hecho es útil cuando no se dispone de computador y, por ello, la simplificación fue bastante usada en los años 60–70’s. También resulta útil cuando, para la evaluación, solo se dispone de datos de mortalidad natural, M, y de parámetros de crecimiento.
2. La simplificación también es usada actualmente para estudiar los efectos de variaciones del coeficiente de mortalidad por pesca, F, y también variaciones de la edad de primera captura, tc, en la biomasa de la cohorte durante toda la vida explotada, en la respectiva captura en peso y en el peso medio de la captura. Estos análisis se suelen ilustrar con gráficos. Por ejemplo la Figura 3.9 ejemplifica el análisis de la biomasa y de la captura en peso obtenidas de una cohorte durante la vida explotada, sujeta a diferentes coeficientes de mortalidad por pesca suponiendo una edad tc fija.

|
Figura 3.9 |
Evolución de la biomasa y de la captura en peso de una cohorte sujeta a diferentes coeficientes de mortalidad por pesca y tc fija (nótese que la Figura 3.9 ilustra simplemente el análisis y no toma en consideración las escalas de los ejes). |
3. Nótese que la forma de las curvas anteriores, Y y Bcum contra F, no dependen del valor del reclutamiento y, por ello, se les suele llamar curvas de biomasa y captura o rendimiento por recluta, B/R e Y/R, respectivamente. Los cálculos por facilidad acostumbran a realizarse para R=1000.
4. De todas las características de la cohorte durante su vida, el peso medio de la captura (así como la edad y la talla medias de la captura) no dependen del reclutamiento. Estas curvas de las características de una cohorte durante su vida contra el nivel de pesca, F, o contra la edad de 1ª captura, tc, merecen un estudio cuidadoso por razones que serán señaladas en el capítulo dedicado a las proyecciones del stock a largo plazo.
5. Bcum se calculo como:
donde 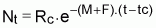 y
y
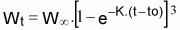
Los cálculos también pueden realizarse, usando un valor de la constante b, de la relación W-L, diferente del coeficiente de isomorfismo, b=3. Para ello se puede recurrir a la función matemática Beta incompleta (Jones, 1957).
6. Para el cálculo de
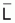 y
y
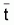 se procede de modo
idéntico al cálculo de
se procede de modo
idéntico al cálculo de
 , esto es,
, esto es,
e
donde:
Estas medias son llamadas medias ponderadas, siendo los factores de ponderación el número de supervivientes Nt en cada edad t.