4.1.1 EVOLUCIÓN DE LA ESTRUCTURA DE EDADES
Se considera la evolución de un stock, constituido por varias cohortes, durante un año. La Figura 4.1 muestra la estructura del stock al inicio del año, las características medias durante el año y la estructura que sobrevive al final del año.

Figura 4.1 Estructura del stock al inicio y al final del año
i = 0,1,2,3, ... representa las edades
4.1.2 CARACTERÍSTICAS DEL STOCK AL INICIO DEL AÑO
Sean:
Ni – el número de individuos de edad i, al inicio del año
wi – el peso individual de la edad i, al inicio del año
Bi – la biomasa total de los individuos de edad i, al inicio del año
N – el número total de supervivientes del stock al inicio del año
B – la biomasa total del stock al inicio del mismo año
Entonces:
4.1.3 CARACTERÍSTICAS DEL STOCK DURANTE EL AÑO
Sean:
|
Mi, Fi e Zi |
coeficientes de mortalidad natural, por pesca y total a la edad i durante el año |
|
|
|
peso medio individual de la edad i durante el año |
|
|
|
número medio de los individuos durante el año |
|
|
|
biomasa media de los individuos durante el año |
|
|
C |
captura, en número, durante el año |
|
|
Y |
captura, en peso, durante el año |
|
|
|
peso individual medio de los individuos capturados durante el año |
|
|
|
peso individual medio de los individuos del stock durante el año |
Entonces:
(donde T=1 año)
(donde T=1 año)
con Ncumi, Ci, Bcumi e Yi calculados para todas las edades i según las expresiones dadas anteriormente en el Capítulo 3 – Cohorte.
4.1.4 CARACTERÍSTICAS DEL STOCK AL FINAL DEL AÑO
El número de individuos de edad i+1 será:
Sea:
R – reclutamiento de la cohorte en el año siguiente
Entonces el número y la biomasa del stock al inicio del año siguiente serán:
y
donde R.W1 es la biomasa del reclutamiento del año siguiente
Comentarios
1. El final del año coincide con el inicio del año siguiente. Así el número de supervivientes de la edad i al final del año será Ni+1.
2. La suma del número total de supervivientes del stock al final del año no es igual al número de individuos del stock al inicio del año siguiente ya que faltan los reclutas que entran en ese año.
3. El número total de muertos, D, durante el
año, seria 
4. Como el intervalo de tiempo es 1 año, los valores acumulables serán iguales a los valores medios, es decir:
5. La utilización de los mismos símbolos N, B, D, etc., para el stock y para la cohorte no debe provocar confusiones.
4.2.1 NIVEL DE PESCA Y PATRÓN DE EXPLOTACIÓN
La acción directa del hombre al pescar un stock se traduce en influenciar los coeficientes Fi de mortalidad por pesca, que están asociados a la cantidad de esfuerzo y a la disponibilidad de los individuos de diferentes tamaños o edades, i, para los artes de pesca usados por las embarcaciones durante el año.
Es costumbre separar los coeficientes de mortalidad por pesca en dos componentes:
Uno llamado nivel de intensidad de mortalidad por pesca,
 , durante el año,
abreviadamente llamado nivel de pesca, F. El nivel está asociado a
la cantidad de esfuerzo de pesca, esto es, al número de
embarcaciones que están pescando, al número de días, de
lances, de horas de pesca durante el año, a la eficacia o poder de pesca
de las embarcaciones o artes de pesca y otro componente, llamado patrón
relativo de explotación, si, asociado a las propiedades
selectivas de los artes de pesca en relación a las tallas o edades de los
individuos disponibles a la captura, durante ese año.
, durante el año,
abreviadamente llamado nivel de pesca, F. El nivel está asociado a
la cantidad de esfuerzo de pesca, esto es, al número de
embarcaciones que están pescando, al número de días, de
lances, de horas de pesca durante el año, a la eficacia o poder de pesca
de las embarcaciones o artes de pesca y otro componente, llamado patrón
relativo de explotación, si, asociado a las propiedades
selectivas de los artes de pesca en relación a las tallas o edades de los
individuos disponibles a la captura, durante ese año.
Al conjunto combinado del nivel de pesca (valor único para todas las edades) y del patrón relativo de explotación (valores diferentes para diferentes tallas o edades) durante un año, se le llama patrón de pesca o régimen de pesca. El patrón de pesca puede confundirse con el patrón relativo de explotación y también el régimen de pesca puede causar confusión con lo que los economistas y gestores llaman régimen de pesca.
Puede decirse que el patrón de pesca, Fi,
durante un año correspondiente a una edad i, es igual al producto del
nivel de pesca de ese año,
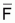 por el patrón
relativo de explotación de cada edad, si. O sea:
por el patrón
relativo de explotación de cada edad, si. O sea:
Los análisis de los efectos del coeficiente de mortalidad por pesca, Fi, sobre las características del recurso y sobre las capturas, normalmente inciden sobre el nivel de pesca, porque se considera que el patrón relativo de explotación se mantiene estable. A veces (como por ejemplo cuando se dan cambios de tamaño de malla de las redes de pesca) se pueden analizar los efectos de cambios en el patrón relativo de explotación manteniendo fijo el nivel de pesca, aunque nada impide que se analicen también los efectos combinados de ambos componentes.
Con el fin de que no existan dudas, el nivel de pesca,
 , se representa simplemente
por F.
, se representa simplemente
por F.
Conociendo la estructura del stock al inicio de un año
se puede, como se ha visto, proyectar las características del stock
durante ese año y estimar la estructura del stock al inicio del
año siguiente (con la excepción del reclutamiento de ese
año), para diferentes valores del nivel de pesca,
 , y del patrón
relativo de explotación, si, aplicados durante el
año.
, y del patrón
relativo de explotación, si, aplicados durante el
año.
Obviamente, es necesario conocer los parámetros biológicos de crecimiento, de madurez sexual y la mortalidad natural a cada edad durante el año.
Adoptando un valor de reclutamiento para el año siguiente, se podría repetir la proyección para ese año y así sucesivamente. El principal inconveniente de proyectar el stock para varios años será que esa proyecciones dependerán cada vez más de los valores de los reclutamientos anuales adoptados. Por eso, en la práctica, se procura proyectar para un, o como mucho, para dos años.
Nótese que para proyectar un stock para el año siguiente es necesario disponer de datos relativos al año anterior. Así, se proyecta primero el stock para el año en curso (determinando sus características al final del año) y después se proyecta la captura y la biomasa para el año siguiente.
Supongamos, por ejemplo, que en 1997 se pretenden proyectar las características del stock para 1998. Como los datos disponibles serán, en la mejor de las hipótesis, referentes a 1996, eso implica que tendrá que proyectarse el stock de 1996 para el inicio de 1997 y conjuntamente con el reclutamiento de 1997 proyectar el stock hasta el final del año1997 y, solo entonces se podrán realizar las proyecciones para 1998, estimándose previamente el reclutamiento de 1998.
Considérese que el vector N y sus componentes N1, N2, ..., Ni, ... representan la estructura del stock al inicio de un año. Nótese que 1,2, ..., i,... designan las edades de los supervivientes de cada una de las cohortes presentes en el stock, al inicio del año.
Sean Mi y Fi los coeficientes de mortalidad natural y por pesca de la edad i, suponiéndolos constantes en años futuros.
La Figura 4.2, ilustra utilizando un stock teórico, las proyecciones del número de supervivientes de las diferentes cohortes presentes al inicio del año 1980, en años sucesivos del periodo 1981–1986 (los valores se expresan en millones de individuos).
Nótese que faltan los reclutamientos que todavía no se han producido, y que entraran en el área de pesca en los años 1981 a 1986. Asimismo, faltan los supervivientes correspondientes a estos reclutamientos en el mismo período de años.
Supongamos ahora que los reclutamientos en estos años fueran iguales al de 1980, esto es, 440 millones de individuos. La Figura 4.3 muestra las proyecciones en los años sucesivos. Se puede constatar que los valores correspondientes a las mismas edades, de la estructura del stock en 1986 y de la evolución de la cohorte de 1980, son iguales.

Figura 4.2 Estructura del stock al inicio de 1980 y proyecciones del número de supervivientes (millones de individuos) de las diferentes cohortes presentes al inicio de los años 1981–1986

Figura 4.3 Proyecciones a Largo Plazo de la cohorte de 1980 y estructura del stock admitiendo un reclutamiento anual constante de 440 millones de individuos
Una conclusión práctica parece ser que para obtener la estructura del stock en 1986 (a LP) bastaría con seguir la evolución de la cohorte de 1980 y, por tanto, no se necesita la estructura completa del stock al inicio del año. Basta adoptar un valor para el reclutamiento (R) de una cohorte (y, por supuesto, suponer estables los parámetros biológicos en los años siguientes). Un consejo puede ser realizar los cálculos adoptando un Reclutamiento de 1000 individuos (con programas de computador se adopta un reclutamiento igual a 1).
Las características del stock a LP en las condiciones anteriores son, en un modelo general, proporcionales al Reclutamiento (con la excepción de los valores medios – edad media, talla media, peso medio en la captura, etc., que son independientes del valor de R). Así estas proyecciones a LP también son llamadas proyecciones por recluta y proyecciones de «equilibrio» o proyecciones a LP.
Las proyecciones a LP no se limitan a los supervivientes al
inicio del año, sino que incluyen también los valores de las
abundancias medias,  ,
durante el año, y las capturas en número,
Ci.
,
durante el año, y las capturas en número,
Ci.
Conociendo los pesos individuales iníciales, Wi
y medios, 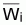 , de las
edades i, y otros parámetros como los de la madurez sexual,
también se pueden proyectar las biomasas totales, B o
, de las
edades i, y otros parámetros como los de la madurez sexual,
también se pueden proyectar las biomasas totales, B o
 , y las biomasas
reproductoras, BD o
, y las biomasas
reproductoras, BD o 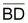 ,
así como las capturas en peso, Y.
,
así como las capturas en peso, Y.
Para efectuar los cálculos de las proyecciones a LP es
importante verificar que los valores acumulados, Ncumi y
Bcumi, de una cohorte durante 1 año son iguales a los valores
medios,  y
y
 , durante ese año.
Así, las principales características del stock, durante 1
año y a LP, se pueden calcular como:
, durante ese año.
Así, las principales características del stock, durante 1
año y a LP, se pueden calcular como:
C = S Ci
Y = S Yi
Utilizando diferentes valores de Fi, o mejor, con
varios niveles de pesca,
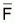 , o varios patrones
relativos de explotación, si, se pueden realizar
diversas proyecciones a LP.
, o varios patrones
relativos de explotación, si, se pueden realizar
diversas proyecciones a LP.
Para los análisis de la influencia del nivel de pesca en las capturas y en el stock, se acostumbra a mantener fijo el patrón relativo de explotación. Por el contrario, cuando se pretende evaluar las consecuencia en el stock y en la captura de una «modificación» del patrón relativo de explotación (cambio de malla, por ejemplo), se mantiene fijo el nivel de pesca y se realizan ensayos con diferentes valores de si. Además, obviamente, también se pueden proyectar los stocks variando simultáneamente los dos componentes del patrón de pesca.
La Figura 4.4 (A-C) muestra varios tipos de curvas a LP de la Producción por Recluta, manteniendo fijo el patrón relativo de explotación. Para otros patrones relativos de explotación las curvas pueden ser diferentes.

|
Figura 4.4 |
Ejemplos de la forma de las curvas de Producción por Recluta (Y/R) contra F, dado un patrón relativo de explotación: (A – con máximo, B – achatada, C – asintótica) |
La Figura 4.5 (A-E) ilustra las relaciones entre las características más importantes del stock y del nivel de pesca, manteniendo estable el patrón relativo de explotación:

|
Figura 4.5 |
Relaciones entre características del stock a Largo Plazo contra el nivel de pesca F, (A – número medio/R, B – captura en número/R, C – peso medio en la captura, D – biomasa media/R, E – captura en peso/R) |
Un análisis más pormenorizado de estas curvas se presentará más adelante, en el capítulo 5.
Conclusión
|
La estructura por edades del stock a LP durante 1 año |
= |
Evolución de la cohorte durante su vida |
Comentarios
1. Para proyectar un stock en un año a LP, suponiendo constantes los reclutamientos anuales, se proyecta una cohorte durante su vida.
2. Es preciso conocer Mi para todas las edades de la cohorte,
así como Wi,
 , si y el nivel de pesca,
, si y el nivel de pesca,
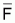 , que se supone constante en
los años siguientes.
, que se supone constante en
los años siguientes.
3. El reclutamiento puede ser cualquiera. Se adopta R = 1000 o R = 1 (con hojas de cálculo para computador).
4. La 5 características del stock más
importantes son  ,
,
 , Cstock,
Ystock y
, Cstock,
Ystock y
 (ver páginas
anteriores de este capítulo para las respectivas expresiones de
cálculo)
(ver páginas
anteriores de este capítulo para las respectivas expresiones de
cálculo)
5. Una característica también importante del stock es la biomasa reproductora, BD. Para calcularla es necesario conocer la ojiva (o histograma) de madurez.
6. La proyecciones a LP también son llamadas situaciones de equilibrio.
7. Proyecciones a LP sirven para definir objetivos de gestión a LP, es decir, metas a alcanzar.
8.  anual
es el mismo cualquiera que sea el reclutamiento (así como
anual
es el mismo cualquiera que sea el reclutamiento (así como
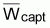 y
y
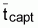 ).
).
9. Además los economistas transforman la captura
total, Y en valor Y$, transforman el peso medio en la captura,
 , en precio del pescado,
, en precio del pescado,
 , o rendimiento por
embarcación (o la CPUE) en valor de la producción por
embarcación, U$, y transforman el nivel de pesca,
, o rendimiento por
embarcación (o la CPUE) en valor de la producción por
embarcación, U$, y transforman el nivel de pesca,
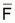 en coste de
explotación, F$. La diferencia entre el valor de la captura y el coste
de explotación, Y$-F$, es el lucro, L$. La Figura 4.6 muestra un
ejemplo de relaciones a LP entre estas características usadas por los
economistas, contra el nivel de pesca,
en coste de
explotación, F$. La diferencia entre el valor de la captura y el coste
de explotación, Y$-F$, es el lucro, L$. La Figura 4.6 muestra un
ejemplo de relaciones a LP entre estas características usadas por los
economistas, contra el nivel de pesca,


|
Figura 4.6 |
Relación a Largo Plazo entre valor de la captura, costo de explotación y lucro contra el nivel de pesca |
La relación stock-reclutamiento, conocida como relación S-R, procura relacionar el tamaño del stock, durante 1 año, con el reclutamiento resultante de la puesta del stock durante ese año. El reclutamiento que interesa para la relación S-R, es el reclutamiento a la fase explotable. Este reclutamiento puede producirse en el mismo año de la puesta que lo originó o desfasarse en uno o más años.
El problema de la relación entre la población parental y la nueva generación no es una cuestión especial de los recursos pesqueros, pues lo es de todas las poblaciones autorenovables.
En cada caso concreto es importante determinar cual es el stock y cual el reclutamiento en cuestión. En efecto, ese stock puede ser el número total de individuos (al inicio del año o el valor medio durante el año), o el número de individuos adultos del stock, o simplemente el número de hembras adultas, etc. También se pueden adoptar, no las abundancias en número, sino las respectivas biomasas. La decisión dependerá del tipo de recurso y de los datos disponibles. También es necesario determinar que tipo de reclutamiento se va ha adoptar. ¿En peso?, ¿en número?, ¿el reclutamiento al área de pesca?, ¿el reclutamiento a la fase explotada?
Simplificando, en este manual, stock (S) será la biomasa (total o adulta) y el reclutamiento (R) se expresara en número de individuos.
Nótese, en primer lugar, que después de la puesta, los individuos de la nueva generación deberán pasar por diferentes fases del ciclo biológico (huevo, larva y juvenil), antes de ser reclutas. Estas fases, que en algunas especies llegan a durar años, no interesan directamente a la explotación pesquera. Por eso, la pesca no afecta directamente al tamaño del nuevo reclutamiento. Es cierto que la pesca actúa sobre el tamaño de la biomasa reproductora que a su vez influencia el próximo reclutamiento, pero la acción de la pesca acontece fuera del intervalo de tiempo en que ocurren las fases pre-recluta mencionadas, y es precisamente para ese intervalo de tiempo para el que se pretende establecer la relación S-R.
En esas fases de pre-reclutamiento existe una gran mortandad debida a factores climáticos y ambientales (vientos, corrientes, temperaturas, etc.) o bien debida a factores biológicos (disponibilidad de alimento, depredación y otros).
La gran variedad de factores («no pesqueros») y sus grandes fluctuaciones hacen que la relación S-R sea compleja y dificultan la creación de un modelo para explicar la relación. En conclusión, la relación S-R, entre stock y reclutamiento resultante, puede considerarse independiente de la pesca.

Figura 4.7 Ejemplo de la dispersión de los puntos en la relación S-R
La Figura 4.7 muestra el tipo de dispersión de valores que se obtiene cuando se representan los reclutamientos (R) contra los stocks parentales (S).
A pesar de las dificultades, se han propuesto algunos modelos para la relación S-R. Una de las razones para ello es que se cree que debe existir una relación. En cualquier caso se conoce un punto de la relación (S = 0, R = 0).
4.5.1 MODELO DE BEVERTON Y HOLT (1957)
Beverton y Holt analizando la pesca de la platija en aguas inglesas propusieron un modelo, que actualmente se acostumbra a escribir de la forma siguiente:

donde a y k son constantes:

Figura 4.8 Relación S-R de Beverton y Holt
Este modelo muestra una curva con R resultante asintótico cuando S®¥.
4.5.2 MODELO DE RICKER (1954)
Ricker estudiando la pesca del bacalao en las costas canadienses propuso otro modelo que se puede escribir de la siguiente forma:
R = a.S.e-S/k
donde a y k son constantes.

Figura 4.9 Relación S-R de Ricker
Este modelo presenta un reclutamiento resultante máximo para un valor intermedio del stock parental, S.
4.5.3 OTROS MODELOS
Hay otras propuestas de modelos de S-R, como es el modelo generalizo de Deriso (1980), que se puede plantear de la forma siguiente (Hilborn & Walters, 1992):
(cuando c = -1 el modelo es el de Beverton y Holt y cuando c®0 el modelo es el de Ricker)
o el modelo generalizo de Shepherd (1982), de la forma:
(cuando c = 1 el modelo es el de Beverton y Holt y cuando c = 2 la curva es una aproximación del modelo de Ricker)
Nótese que en todos los modelos mencionados, para S=0, R=0, como era de esperar y la pendiente de la tangente a la curva en ese punto, (0,0), es igual al parámetro a. A veces, las relaciones S-R se presentan en forma de R/S en función de S.
Así la ecuación de Beverton y Holt seria:
mostrando que el inverso de R/S es lineal con S.
Con el modelo de Ricker la relación entre R/S contra S seria:
o sea, R/S es exponencial negativa con S (el ln(R/S) es lineal con S).
En el caso del modelo de Deriso seria (R/S)c lineal con S.
Matemáticamente estas últimas relaciones pueden ser útiles, por su simplicidad, pero estadísticamente pueden presentar el inconveniente de la variable S que puede aparecer tanto en la variable dependiente como en la variable independiente.
Comentarios
1. Reacuérdese que las relaciones S-R son independientes del nivel de pesca.
2. Las relaciones S-R pueden ser introducidas en los cálculos de las proyecciones del stock. En ese caso, las proyecciones a Corto Plazo deberán realizarse año a año y exigen la estructura del stock al inicio del año.
3. No se debe olvidar que existe una gran dispersión de los puntos (S, R) alrededor del modelo.
4. En el modelo de Deriso cuando c = -1 el modelo es el de Beverton y Holt; cuando c ® 0 el modelo tiende al de Ricker (para demostrar el límite de la ecuación de Deriso cuando c ® 0 basta recordar que límite (1+A/n)n = eA cuando n ® ¥ y A es una constante).
5. El modelo de Beverton y Holt matemáticamente presenta una asíntota, R ® a.k cuando S ® ¥. El valor de R dado por este modelo cuando S = k toma el valor de R = a k/2.
El modelo de Deriso presenta el máximo:
Smax = k / (1+c), Rmax = a.k / (1+c)1+(1/c)
El modelo de Shepherd presenta el máximo:
Smax = k.(c-1)-1/c, Rmax = (a /c).k.(c-1)1-(1/c)
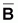 resultante
(relación R-S)
resultante
(relación R-S)La relación S-R sigue siendo objeto de discusión, en concreto la relación entre la biomasa S y el reclutamiento R resultante. Hay otra relación (ya mencionada en la sección 4.4 (Stock: proyecciones a LP, particularmente en la conclusión sobre la estructura del stock y la evolución de una cohorte durante toda su vida) a la que se podría llamar relación R-S, o sea, la relación entre el reclutamiento R y la biomasa resultante acumulada, Bcum, de una cohorte durante toda la vida explotada para un nivel de pesca dado.
La biomasa (o biomasa reproductora) acumulada de una cohorte durante su vida, Bcum o BDcum es como ya se vio, igual a:
Bcum= R. {función de parámetros biológicos y del patrón de pesca, F}
Por otro lado, ya se indicó que la biomasa acumulada,
Bcum, de una cohorte durante su vida es igual a la biomasa
media,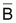 , del stock
durante un año, a Largo Plazo. Por eso es conveniente referirse a la
Bcum
como
, del stock
durante un año, a Largo Plazo. Por eso es conveniente referirse a la
Bcum
como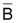 .
.
Así, se puede decir que: si los parámetros biológicos fueran considerados constantes entonces, para un patrón de pesca dado la biomasa media durante un año de un stock a LP es proporcional al reclutamiento. La Figura 4.10 ilustra la proporcionalidad.

|
Figura 4.10 |
Ilustración de la proporcionalidad entre la Biomasa
media ( |
Nótese que en la Figura 4.5-D, se presenta la
relación en la forma
 /R contra F. Las dos curvas
4.5-D y la Figura 4.10 son representaciones diferentes de la misma
situación, es decir, para un F dado la curva de la Figura 4.5-D da el
valor de
/R contra F. Las dos curvas
4.5-D y la Figura 4.10 son representaciones diferentes de la misma
situación, es decir, para un F dado la curva de la Figura 4.5-D da el
valor de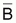 /R mientras que la
recta de la Figura 4.10 para un valor
de
/R mientras que la
recta de la Figura 4.10 para un valor
de /R (pendiente de la recta)
dado da el valor de F.
/R (pendiente de la recta)
dado da el valor de F.
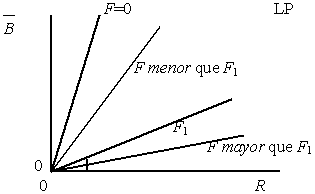
Para otros valores de F, la recta tendrá inclinaciones diferentes. La Figura 4.11 muestra varias rectas para diferentes valores de F.
|
Figura 4.11 |
Ilustración de cuatro situaciones a LP para diferentes niveles de pesca, F |
La curva de la Figura 4.9 y la recta de la Figura 4.10 pueden superponerse en un mismo gráfico. La Figura 4.12 muestra esa superposición, o sea, la superposición de la curva S-R de Ricker con la recta R-S (nótese que en la Figura 4.12 las posiciones de los ejes correspondientes a la Figura 4.10 han sido cambiados y, por eso, cuando se menciona la pendiente de la recta se debe indicar que se trata de la pendiente con el eje R).
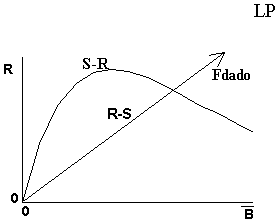
Figura 4.12 Superposición de la curva S-R con la recta R-S para un F dado
Para evitar confusiones entre las dos relaciones, S-R representa la relación entre la biomasa y el reclutamiento resultante y R-S la relación entre el reclutamiento y la biomasa media a LP.
Con este modelo se puede ilustrar el análisis combinado
entre las dos relaciones a LP con un nivel de pesca dado. Para una biomasa dada,
la relación S-R determina el reclutamiento futuro, reclutamiento que a su
vez, dará origen a LP a una
biomasa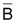 resultante a
través de la relación R-S, y así sucesivamente hasta
encontrar una situación de equilibrio.
resultante a
través de la relación R-S, y así sucesivamente hasta
encontrar una situación de equilibrio.
Por ejemplo, seleccionemos un
valor . La curva S-R permite
calcular el valor de R2 resultante. A ese valor de R2
corresponderá a través de la recta (para un F dado) el valor
de
. La curva S-R permite
calcular el valor de R2 resultante. A ese valor de R2
corresponderá a través de la recta (para un F dado) el valor
de resultante a LP, y
así sucesivamente. En la Figura 4.13, Se puede verificar que el proceso
encontrara el punto de equilibrio (RE,
resultante a LP, y
así sucesivamente. En la Figura 4.13, Se puede verificar que el proceso
encontrara el punto de equilibrio (RE,
 ). Este punto
correspondería a un valor del nivel de pesca F. Este valor de F puede
determinarse por la pendiente de la recta en relación al eje R y por la
relación a LP de
). Este punto
correspondería a un valor del nivel de pesca F. Este valor de F puede
determinarse por la pendiente de la recta en relación al eje R y por la
relación a LP de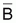 /R
contra F.
/R
contra F.

|
Figura 4.13 |
Ilustración de los sucesivos puntos que, partiendo
de una biomasa |
La intersección de las dos relaciones no siempre conduce a un punto de equilibrio. La existencia de un punto de equilibrio depende del ángulo en la intersección entre la recta y la curva en el punto de intersección.