En los capítulos anteriores se han analizado varios modelos usados en la evaluación de stocks, definiéndose los respectivos parámetros. En las correspondientes fichas de ejercicios los valores de los parámetros se dieron por conocidos, no siendo necesario estimarlos. En este capítulo se analizarán los diversos métodos para estimar los parámetros. Conviene recordar que la estimación de parámetros implica conocimientos sobre a teoría de muestreo y sobre inferencia estadística.
En este manual se referirá uno de los métodos generales mas usados en la estimación de parámetros – el método de los mínimos cuadrados. Este método utiliza, en muchos casos, procesos iterativos de estimación que requieren valores iniciales próximos a los verdaderos parámetros. Así, se presentan también algunos métodos particulares, que permiten obtener, fácilmente, estimaciones próximas a los verdaderos valores de los parámetros. De cualquier modo, estas estimaciones aproximadas también tienen, por si solas, interés práctico. Estos métodos serán ilustrados con la estimación de los parámetros de crecimiento y de la relación stock-reclutamiento, S-R.
El método de los mínimos cuadrados es presentado bajo las formas de Regresión lineal simple, del modelo lineal múltiple y de modelos no lineales (método de Gauss-Newton).
Asuntos como el análisis de residuos, distribución en el muestreo de los estimadores (asintóticas o empíricas «Bootstrap» y «jacknife»), limites y intervalos de confianza, etc., son importantes en la estimación de parámetros. No obstante, para abordar estos asuntos, seria necesario un curso de mayor duración.
Modelo
Considerando las siguientes variables y parámetros:
|
|
|
Variable dependiente (o respuesta) |
= Y |
|
|
|
Variable independiente (o auxiliar) |
= X |
|
|
|
Parámetros |
= A, B |
|
|
La variable independiente es lineal con los parámetros |
|
|
|
|
|
Y = A+BX |
|
Objetivo
Observados n pares de valores (cada par esta constituido por un valor seleccionado de la variable independiente y el valor observado correspondiente a la variable dependiente) estimar los parámetros del modelo o sea:
|
Observados |
xi e yi para cada par i, como i = 1, 2,..., i,...n |
|
Estimar |
A y B y (Y1, Y2,..., Yi,..., Yn) para los n pares de valores observados |
|
(Valores estimados |
|
Función objeto (o función criterio)
Criterio de estimación
Los estimadores serán los valores de A y B que hacen mínima la función objeto. Este criterio se denomina método de los mínimos cuadrados. Para llevar a cabo la minimización han de igualarse a cero las derivadas ¶F/¶A y ¶F/¶B y resolver el sistema de ecuaciones obtenido respecto A y B.
La resolución del sistema de ecuaciones, después de algunas transformaciones matemáticas, da los siguientes resultados:
|
|
|
|
|
|
Sxx = S(x
- |
Sxy = S(x
- |
|
|
b = Sxy/Sxx |
a = |
Nótese que los valores yi observados, para un mismo conjunto de valores de X seleccionados, dependen de la muestra recogida. Estadísticamente se acostumbra a presentar el problema de la regresión lineal simple escribiendo el modelo como:
y = A + BX + e
donde e es una variable aleatoria con valor esperado igual a cero y varianza igual a s2.
Así, el valor esperado de y será Y o A+BX y la varianza de y será igual a la varianza de e.
Se acostumbra a diferenciar desvío de residuo:
Desvío es la diferencia de yobservado e
ymédio (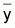 ),
esto es desvío =
(y-
),
esto es desvío =
(y-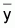 )
)
En tanto que
Residuo es la diferencia entre yobservado e
Yestimado (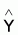 ),
esto es residuo = (yi
-
),
esto es residuo = (yi
-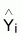 ).
).
Es conveniente, para el análisis del ajuste del modelo a los datos observados, considerar las siguientes características:
La suma de los cuadrados de los residuos:
Esta cantidad indica la variación residual de los valores observados en relación a los valores estimados del modelo, esto es, la variación de los valores observados no explicada por el modelo.
La suma de los cuadrados de los desvíos de los valores estimados del modelo es igual a:
Este valor indica la variación de los valores estimados de la variable dependiente del modelo en relación a su media, esto es, la variación de los valores estimados de la variable dependiente explicada por el modelo.
La suma total de los cuadrados de los desvíos de los valores observados es igual a:
Este valor indica la variación total de los valores observados en relación a la media
Es fácil verificar la siguiente relación:
SQtotal = SQmodelo + SQresidual
o
o
1 = r2 + (1 - r2)
donde
r2 (coeficiente de determinación) es el porcentaje de la variación total que es explicada por el modelo y,
1-r2 es el porcentaje de la variación total que no es explicada por el modelo.
Modelo
Considerando las siguientes variables y parámetros:
|
|
Variable dependiente (o de respuesta) |
= Y |
|
|
Variables independientes (o auxiliares) |
= X1, X2,..., Xj,..., Xk |
|
|
Parámetros |
= B1, B2,..., Bj,..., Bk |
La variable dependiente es lineal con los parámetros
Y = B1X1+B2X2+... + BkXk = SBjXj
Objetivo
Observados n conjuntos de valores (cada conjunto esta constituido por un valor observado de cada variable independiente y el valor observado correspondiente de la variable dependiente), estimar los parámetros del modelo, o sea:
|
Observados |
x1,i x2,i,..., xj,i,.., xk,i e yi para cada conjunto i, con i=1,2,...,i,...n |
|
Estimar |
B1,B2,...,Bj,...,Bk e (Y1,Y2,..., Yi,..., Yn) para los n conjuntos observados |
|
Los valores estimados pueden ser representados por: |
|
|
|
|
Función objeto o función criterio
Criterio de estimación
Los estimadores serán los valores de Bj que minimizan la función objeto. Este criterio es el llamado método de los mínimos cuadrados.
De un modo semejante al usado en el caso del modelo lineal simple, el procedimiento de minimización debe igualar a cero las derivadas parciales de F respecto a cada parámetro, Bj con j=1, 2,..., k. Este procedimiento es, preferentemente, tratado con el cálculo matricial.
Forma matricial
Matriz
Matriz de los valores observados de las variables independientes
Vector
Vector de los valores observados de la variable dependiente
Vector
Vector de los valores de la variable dependiente (no observados)
Vector
Vector de los parámetros
Vector
o
Vector de los estimadores de los parámetros
Modelo
Y(n,1) = X(n,k). B(k,1) o Y=X.B+e
Función objeto
|
|
F(1,1) = (y-Y)T.(y-Y) o |
F(1,1) = (y-X.B)T.(y-X.B) |
Para calcular los estimadores de los mínimos cuadrados basta igualar a cero la derivada de F respecto al vector B. Recuérdese que dF/dB es un vector con componentes ¶F/¶B1, ¶F/¶B2,..., ¶F/¶Bk. El resultado es:
|
|
|
dF/dB(k,1) = -2.XT.(y-X.B) = 0 |
|
|
o |
XTy - (XT.X). B = 0 |
|
|
|
|
Los resultados se pueden expresar como:
|
|
b(k,1) = (XT.X)-1.XTy |
|
|
|
|
|
|
|
residuos(n,1) =
(y- |
|
Comentarios
Para el análisis estadístico es conveniente expresar los estimadores y las sumas de los cuadrados utilizando matrices idempotentes. Al utilizar las matrices idempotentes L, (I - L) y (I - M) con L(n,n) = X (XT. X)-1. XT, I = matriz unitaria y M(n,n) = matriz media(n,1) = 1/n [1] donde [1] es una matriz con todos los elementos iguales a la unidad.
También es importante considerar las distribuciones de los estimadores en el muestreo y suponer que los valores ei son independientes y con distribución normal.
Es conveniente mencionar aquí algunas propiedades del valor esperado y de la varianza de una relación lineal de una variable aleatoria u. En términos matriciales se considera c1 un vector constante de dimensión (n.1), c2 una matriz de valores constantes de dimensión (n.n) y el vector aleatorio u de dimensión (n.1). Así, resulta:
|
|
E[c1+c2.u] = c1+c2.E[u] |
V[c1+c2.u] = c2.V[u].c2T |
|
1 – |
Variable aleatoria, e |
en. (independientes) |
|
|
Valor esperado de e |
E[e] = 0. |
|
|
Varianza de e igual a |
V[e](n.n) = E[e.eT]=I. s2 |
|
2 – |
Variable dependiente y observada |
y = Y+e |
|
|
Valor esperado de y |
E[y] = Y = X.B. |
|
|
Varianza de y igual a |
V[y](n.n) = V[e](n.n) = I. s2 |
|
3 – |
Estimador del vector parámetro B |
|
|
|
Valor esperado de
|
E[ |
|
|
Varianza de
|
V[ |
|
4 – |
Estimador de Y del modelo |
|
|
|
Valor esperado de
|
E[ |
|
|
Varianza de
|
V[ |
|
5 – |
Residuo e |
e = y- |
|
|
Valor esperado de e |
E[e] = 0 |
|
|
Varianza de e |
V[e] = (I-L). s2 |
6 – Suma de cuadrados
6.1 –
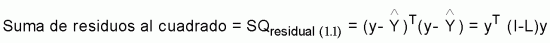
Esta suma indica la variación residual de los valores observados en relación a los valores del modelo, esto es, la variación no explicada por el modelo.
6.2 – Suma de los cuadrados del modelo =
SQmodelo (1.1) =
( -
- )T(
)T(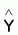 -
-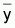 )
= yT (L-M)y
)
= yT (L-M)y
Esta suma indica la variación de los valores del modelo en relación a la media, esto es, la variación explicada por el modelo.
6.3 – Suma total de los cuadrados de los
desvíos = SQtotal (1.1) =
(y-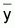 )T(y-
)T(y- )
= yT (I-M) y
)
= yT (I-M) y
Esta suma indica la variación total de los valores observados en relación a la media.
SQtotal = SQmodelo + SQresidual o
o
1 = R2 + (1 - R2)
donde:
R2 es el porcentaje de la variación total que es explicada por el modelo. En forma matricial será:
R2 = [yT(L - M)y].[ (yT(I - M)y]-1
1-R2 es el porcentaje de la variación total que no es explicada por el modelo.
Los valores característicos de las matrices (I-L), (I-M) y (L-M) respectivamente iguales a (n-k), (n-1) y (k-1), son los grados de libertad asociados a las respectivas sumas de los cuadrados.
Modelo
Consideremos las siguientes variables y parámetros:
Variable dependiente (o de respuesta) = Y
Variable independiente (o auxiliar) = X
Parámetros = B1, B2,..., Bj,..., Bk
La variable dependiente es no-lineal con las variables independientes
Y = f(X;B) donde B es un vector de componentes B1, B2,..., Bj,..., Bk
Objetivo
Observados n pares de valores (cada par esta constituido por un valor seleccionado de la variable independiente y el valor observado correspondiente de la variable dependiente) estimar los parámetros del modelo, o sea:
|
Observados |
xi e yi para cada par i, siendo i = 1, 2,..., i,... n |
|
Estimar |
B1, B2,..., Bj,.., Bk e (Y1, Y2,..., Yi,..., Yn) para los n pares de valores observados. |
|
|
(Valores estimados =
|
Función objeto o función criterio
Criterio de estimación
Los estimadores serán los valores de Bj que hacen mínima la función objeto.
(Este criterio se denomina método de los mínimos cuadrados).
Forma matricial
Es conveniente presentar el problema utilizando matrices y aplicando el cálculo matricial. Así:
Vector X(n,1) = Vector de los valores observados de la variable independiente
Vector y(n,1) = Vector de los valores observados de la variable dependiente
Vector Y(n,1) = Vector de los valores de la variable dependiente dados por el modelo
Vector B(k,1) = Vector de los Parámetros
Vector b(k,1) = Vector de los estimadores de los parámetros
Modelo
Y(n,1) = f(X; B)
Función objeto
F(1,1) = (y-Y)T.(y-Y)
En el caso del modelo no lineal el sistema de ecuaciones resultantes de igualar a cero la derivada de la función F respecto al vector B generalmente no es simple de resolver. La estimación por medio del método de los mínimos cuadrados podrá, no obstante, realizarse recurriendo a algunas modificaciones basadas en el desarrollo de la función Y en serie de Taylor, como una aproximación al modelo.
Revisión a partir del desarrollo de Taylor
Se ejemplifica el desarrollo de una función en serie de Taylor usando el caso más simple de una función de una variable.
La aproximación de Taylor se traduce en desarrollar una función Y = f(x) en torno de un punto seleccionado, x0, en serie de potencias de x:
Y = f(x) = f(x0) +(x-x0).f’(x0)/1! + (x-x0)2f’’(x0)/2! +... + (x- x0)i f(i)(x0)/i!+...
donde
f(i)(x0) = derivadas de f(x) con respecto a x, en el punto x0.
El desarrollo se aproxima a la potencia deseada. Cuando el desarrollo se aproxima a la potencia 1 se dice que se trata de la aproximación lineal de Taylor, o sea,
Y @ f(x0) + (x-x0).f’(x0)
El desarrollo de Taylor se puede aplicar a funciones de más de una variable. Por ejemplo, para una función Y = f(x1,x2), el desarrollo lineal seria:

que, en términos matriciales se puede expresar como:
Y = Y(0)+A(0).(x-x(0))
donde Y(0) es el valor de la función en el punto x(0) de componentes (x1-x1(0)) y (x2-x2(0)) y A(0) es la matriz de derivadas con componentes iguales a la derivada parcial de f(x1,x2) respecto a x1,x2 en el punto (x1(0), x2(0)).
En el caso de la estimación de parámetros el desarrollo de la función Y en serie de Taylor se realiza con respecto a los parámetros B y no al vector X.
Por ejemplo, el desarrollo lineal de Y = f(x,B) respecto a B1, B2,..., Bk, seria:
Y = f(x;B) = f(x; B(0)) + (B1-B1(0)) ¶f /¶B1 (x;B(0)) +..... +
(B2-B2(0)) ¶f / ¶B2 (x;B(0)) +...... +..........+ (Bk-Bk(0)) ¶f /¶Bk (x;B(0))
o puesto en términos matriciales seria:
Y(n,1) = Y(0) (n,1) + A(0) (n,k). DB(0) (k,1)
donde
A = matriz de orden (n, k) de las derivadas parciales de la matriz f(x; B) respecto al vector B en el punto B(0) y
DB(0) = vector (B - B(0)).
Entonces la función objeto será:
F = (y-Y)T.(y-Y) = (y-Y(0) - A(0).DB(0))T(y-Y(0) - A(0).DB(0))
Para obtener el mínimo de esta función es más conveniente derivar (respecto al vector DB que respecto al vector B y igualar a cero. Así resulta:
0 = -2(A(0))T(y-Y(0) -A(0).DB(0)) = -2A(0)T(y-Y(0))+ 2A(0)TA(0).DB(0)
o
A(0)TA(0).DB(0) = A(0)T(y-Y(0))
y por tanto será:
Si DB(0) fuere «igual a cero» entonces es porque el estimador de B es igual a B(0).
(conviene dejar claro que en la práctica cuando se dice «igual a cero» en este proceso, quiere decir «menor que aprox» donde aprox es el vector de aproximación que se quiera definir).
Caso contrario el nuevo valor de B será:
B(1) =B(0) + DB(0)
y el proceso se repite, esto es, se procede a nueva iteración con B(0) substituido por B(1) (y A(0) substituido por A(1)). El proceso iterativo continuará hasta que se verifique la convergencia deseada.
Comentarios
1. El proceso puede no converger siempre. A veces no converge, otras veces es demasiado lento (¡incluso para computadoras!) y otras veces converge ¡pero ha otro limite!
2. El método descrito es el método de Gauss-Newton que es la base de otros muchos métodos. Algunos de estos métodos introducen modificaciones para obtener una convergencia mas rápida como es el caso del método de Marquardt (1963), bastante usado en investigación pesquera. Otros métodos usan el desarrollo de Taylor de segundo orden (método de Newton-Raphson), procurando así una mejor aproximación. Otros, combinan las dos modificaciones.
3. Estos métodos necesitan que se calculen derivadas de las funciones. Algunos programas de computador requieren la introducción de las expresiones matemáticas de las derivadas, otros utilizan subrutinas con aproximaciones numéricas de las derivadas.
4. Conviene también destacar que, en el caso que se pretenda usar métodos iterativos en modelos no-lineales, existen métodos en la investigación pesquera, estudiados en este curso, para calcular valores iniciales de varios parámetros, como por ejemplo, crecimiento, mortalidades, curvas de selectividad y de madurez,
5. De cualquier modo es importante destacar un aspecto común a los métodos iterativos: el valor inicial del vector B(0) usado en el proceso debe ser seleccionado lo mas próximo posible del verdadero valor. De este modo, no solo la convergencia es más rápida sino que también es mas seguro que terminará en el limite deseado.
El método de los mínimos cuadrados (regresión no-lineal) permite estimar los parámetros K, L¥y to de las ecuaciones de crecimiento individual.
Los valores iniciales de K, L¥y t0 pueden ser obtenidos por medio de la regresión lineal simple usando los métodos siguientes.
Métodos de Ford-Walford (1933–1946) y de Gulland y Holt (1959)
Las expresiones de Ford-Walford y de Gulland y Holt, que fueron presentados en la Sección 3.4, ya se expresan en su forma lineal, permitiendo así estimar los valores iniciales de K y L¥ con métodos de regresión lineal simple. La expresión de Gulland y Holt permite estimar K y L¥ incluso cuando los intervalos de tiempo Ti no son constantes. En este caso es conveniente rescribir la expresión como:
DL/Ti = K.L¥- K.
Método de Stamatopoulos y Caddy (1989)
Estos autores presentan también un método para estimar K, L¥y to (o Lo) usando la regresión lineal simple. Para ello la ecuación de von Bertalanffy es expresada como una relación lineal de Lt contra e-Kt.
Se consideran n pares de valores ti, Li donde ti es la edad y Li la talla del individuo i para i=1,2,...., n.
La ecuación de von Bertalanffy, en su forma general, como se vio, es:
L¥- Lt = (L¥- La). e-K(t-ta)
Pudiendo ser escrita en la forma:
Lt = L¥- (L¥- La). e+Kta. e-Kt
Como se puede ver la ecuación anterior es de la forma lineal simple, y = a + bx, donde:
|
|
y = Lt |
a = L¥ |
b = - (L¥- La). e+Kta |
|
|
x = e-Kt |
|
|
Si se adopta La = 0, ta=to, y en contrapartida si se adopta ta = 0, La = Lo.
De cualquier modo los parámetros a estimar a partir de a y b serán L¥, to o Lo.
Así los autores proponen adoptar un valor de K, esto es, K(0), y por regresión lineal simple entre y (= Lt) y x(=e-Kt) estimar a(0), b(0) y r2(0). El procedimiento puede repetirse para varios valores de K, esto es, K(1) K(2),.... Entonces se puede adoptar la regresión para la que resulte el mayor valor de r2, a la cual corresponderá Kmax y amax y bmax. Estos valores de amax, bmax y Kmax permitirán obtener los valores de los restantes parámetros.
Un proceso práctico para encontrar Kmax podrá ser:
(i) Seleccionar dos valores extremos de K que incluyan el valor pretendido, por ejemplo K= 0 y K=2 (por dificultades prácticas conviene usar K = 0.00001 en vez de K = 0).
(ii) Calcular las 10 regresiones para valores de K comprendidos entre tales extremos en intervalos iguales
(iii) Los correspondientes 10 valores de r2 obtenidos permitirán seleccionar dos nuevos valores de K que determinan un intervalo menor del de (i) conteniendo el valor de r2 máximo obtenido
(iv) Los pasos (ii) y (iii) se pueden repetir hasta obtener un intervalo de valores de K con la aproximación deseada. En general este paso no necesita de muchas repeticiones.
Existen varios métodos propuestos para estimar M, basados en la asociación de M con otros parámetros biológicos del recurso. Estos métodos producen resultados aproximados, cuyas aproximaciones dependen de las especies y de los stocks.
7.5.1 RELACIÓN DE M CON LA LONGEVIDAD,
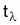
Longevidad: Edad máxima media de los individuos de la población en un stock no explotado.
Duración de la vida explotable:
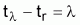 (Figura
7.1)
(Figura
7.1)

Figura 7.1 Duración de la vida explotable
Tanaka (1960) propone Curvas de Supervivencia «NATURAL» (Figura 7.2) para obtener valores de M a partir de la longevidad.
En la práctica se puede considerar que una cohorte se
extingue cuando solo sobrevive una fracción, p, de los individuos
reclutados. En tal caso, partiendo de
 , se puede
escribir:
, se puede
escribir:
y por tanto M = -(1/l).ln p
Diferentes valores de la fracción p de supervivencia producen diferentes curvas de supervivencia de M en función de ë.
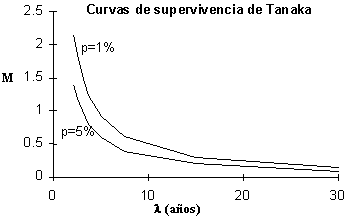
Figura 7.2 Curvas de supervivencia de Tanaka
La selección del valor de p es arbitraria, pero se puede tomar p = 5% (i.e. uno de cada veinte reclutas sobrevive hasta la edad tl).
7.5.2 RELACIÓN ENTRE M Y EL CRECIMIENTO
Método de Beverton y Holt (1959)
Gulland (1969) menciona que Beverton y Holt verificaron que la especies con mayor tasa de mortalidad M presentaban mayores valores de K. Estableciendo una relación simple entre estos dos parámetros, concluían que se podía afirmar que aproximadamente:
para pequeños pelágicos
para peces demersales
Método de Pauly (1980)
Basándose en las siguientes consideraciones:
1. Recursos con una tasa de mortalidad elevada no pueden tener una talla máxima muy grande;
2. En aguas mas calidas, el metabolismo es mas acelerado, de modo que es posible crecer hasta un tamaño mayor y alcanzar el tamaño máximo mas rápidamente de lo que se alcanzaría en aguas mas frías.
Pauly recopilo, en la literatura, datos sobre estos parámetros, para 175 especies y ajusto regresiones múltiples de valores transformados de M contra los correspondientes valores transformados de K, L¥ y de la temperatura, con el fin de encontrar una relación lineal y seleccionó la que consideró con el mejor ajuste, o sea, la siguiente relación empírica:
con los parámetros expresados en las siguientes unidades:
M = año-1
L¥= cm de talla total
K = año-1
T° = temperatura de las aguas en superfície en °C
Pauly llama la atención en cuanto a la prudencia necesaria al aplicar esta expresión a pequeños pelágicos y crustáceos. El primer coeficiente (-0.0152) de la expresión anterior, escrita con logaritmos neperianos, toma un valor diferente al escribirla usando logaritmos decimales.
7.5.3 RELACIÓN ENTRE M Y LA REPRODUCCIÓN
Método de Rikhter y Efanov (1976)
Estos autores analizaron la dependencia entre M y la edad de 1ª madurez a partir de datos representativos de especies de vida corta, media y larga, encontrando una dependencia de M con la edad de 1ª madurez que transformaron en la siguiente relación empírica:
|
|
|
(Unidades) |
|
|
|
|
Método de Gundersson (1980)
Basado en la suposición de que la tasa de mortalidad natural debe estar relacionada con la inversión que hacen los peces en la reproducción, independientemente de la influencia de otros factores, Gundersson estableció varias relaciones entre M y tales factores.
Propuso, la siguiente relación empírica, usando el Índice Gonadosomático (IGS) (estimado para hembras maduras en la época de puesta) para obtener una estimación de M:
7.5.4 DADA LA ESTRUTURA POR EDADES DEL STOCK, AL INICIO Y AL FINAL DEL AÑO, Y LAS CAPTURAS EN NÚMERO POR EDADES DURANTE ESE AÑO
Podemos calcular los coeficientes de mortalidad natural Mi para cada edad i y durante el año, con el procedimiento siguiente:
calcular
calcular
calcular
Loa valores de M obtenidos a cada edad podrán ser comparados y posiblemente combinados para calcular un valor constante, M, para todas las edades.
Método de Paloheimo (1961)
Cuando se conocen fi y Zi para varios años i, y suponiendo que Fi es proporcional a fi,
para
año,
,
entonces:
Así, la regresión lineal entre Zi y fi tiene una pendiente b = q y ordenada en el origen a = M.
Existen varios métodos para estimar el coeficiente de mortalidad total, Z, supuesto constante durante un cierto intervalo de edades o de años.
Es conveniente agrupar los métodos, de acuerdo con los datos de base, atendiendo a los que utilizan edades y los que utilizan tallas.
7.6.1 MÉTODOS CON DATOS POR EDADES
Los diferentes métodos toman como punto de partida la expresión general del número de supervivientes de una cohorte, en el instante t, sometida a mortalidad total, Z, durante un intervalo de tiempo, es decir:
para el intervalo de tiempo (ta,tb) donde Z se supone constante.
Aplicando logaritmos a esta expresión y reorganizando los términos, resulta:
lnNt = Cte - Z.t
donde Cte es constante (= ln Na+Zta).
Esta expresión muestra que el logaritmo del número de supervivientes es lineal con la edad, siendo la pendiente igual a -Z.
La Cte no tiene especial interés para la determinación de Z. En toda expresión las constantes que no interesen para la determinación de Z aparecerán como Cte.
1. Si, dentro del intervalo (ta,tb), Z
puede ser considerado constante y se dispone de datos de abundancia,
 , o índices de
abundancia en
número,
, o índices de
abundancia en
número, , para varias
edades, i, entonces la aplicación de la técnica de la
regresión lineal simple permite estimar el coeficiente de mortalidad
total Z.
, para varias
edades, i, entonces la aplicación de la técnica de la
regresión lineal simple permite estimar el coeficiente de mortalidad
total Z.
En efecto
por tanto
= Ni. Constante
y, como
entonces substituyendo resulta:
(Ti = const = 1 año)
y, por tanto, también será
y la regresión lineal simple entre
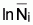 y Ti
permite estimar Z (la constante, Cte, es diferente de la anterior aunque
en realidad para estimar Z solo interesa la pendiente).
y Ti
permite estimar Z (la constante, Cte, es diferente de la anterior aunque
en realidad para estimar Z solo interesa la pendiente).
2. En caso que las edades no sean a intervalos constantes, la expresión podrá plantearse usando los valores de tcentrali, de forma aproximada. Para Ti variable será:
» Ni. e-ZTi/2
y, como
Ni = Na. e -Z.(ti-ta)
será
» Cte. e-Z.tcentrali
y, finalmente:
ln
» Cte - Z.tcentrali
3. En el caso de los
índices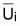 la
situación es semejante ya que
la
situación es semejante ya que
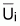 = q.
= q.
 , con q constante, y, por
tanto, también será:
, con q constante, y, por
tanto, también será:
y la regresión lineal simple entre
 y Ti permite
estimar Z.
y Ti permite
estimar Z.
4. En el caso que las edades no sean a intervalos constantes la expresión deberá ser modificada del siguiente modo:
ln
» Cte - Z. tcentrali
Con datos de capturas, Ci, y de edades, ti, sigue siendo posible aplicar la regresión lineal simple para obtener Z, aunque en este caso, será necesario suponer que Fi es constante.
Reacuérdese que Ci = Fi
 Ti y así,
lnCi = Cte + ln
Ti y así,
lnCi = Cte + ln cuando Ti es constante. Por tanto:
cuando Ti es constante. Por tanto:
lnCi = Cte - Z. Ti
5. En el caso que las edades no estén separadas en intervalos constantes la expresión deberá ser modificada del siguiente modo:
lnCi/Ti » Cte - Z. tcentrali
6. Si Vi es la captura acumulada desde ti hasta el final del ciclo vital, (forma conveniente para los cálculos de varias capturas acumuladas) es decir:
Vi = SCk = SFk Nkcum,
donde el sumatorio abarca desde la última edad hasta la edad i.
Como Fk y Zk se suponen constantes (...)Nkcum = Ni/Z y por tanto será:
Vi = FNi/Z y lnVi = Cte + lnNi
Por tanto:
ln Vi = Cte - Z. Ti
7. Finalmente se debe mencionar que Beverton y Holt (1956) también demostraron que:

y, por tanto, es posible estimar Z a partir de la edad
media 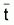
(esta expresión se ha derivado considerando tb = ¥ en el intervalo (ta, tb).
7.6.2 MÉTODOS CON DATOS POR TALLAS
Cuando en vez de datos por edades se dispone de datos por clases de tallas, si bien los métodos referidos anteriormente pueden ser aplicados, conviene acudir al concepto de edad relativa.
Usando la ecuación de von Bertalanffy se puede obtener la edad t en función de la talla, del siguiente modo:
(la expresión debe ser escrita en la forma general en relación a ta y no a t0)
o
(Esta ecuación es citada por algunos autores como ecuación inversa de von Bertalanffy).
A la diferencia t-ta, se le da el nombre de edad relativa, t*.
Así: t* =-(1/K).ln[(L¥- Lt)/(L¥- La)] =-(1/K)ln[1-(Lt-La)/ (L¥- La)]
para ta = t0 seria La = 0 y:
En efecto, esta edad es relativa, ya que difiere de la edad absoluta en una cantidad constante, ta. Así, por ejemplo, la duración del intervalo Ti tanto puede ser calculada por la diferencia de las edades absolutas de los extremos del intervalo, como por la diferencia de las edades relativas:
Ti = ti+1 -ti = t*i +1 - t*i
y este intervalo corresponde al tiempo que el individuo tarda en crecer entre Li y Li+1, es decir, Ti es el tamaño del intervalo i. O también:
t*centrali = tcentrali + Cte
* =
+ Cte
Así las expresiones anteriores se mantienen cuando se substituyen las edades absolutas por edades relativas:
ln
= Cte - Z. t*centrali
ln= Cte - Z. t*centrali
ln Vi = Cte - Z. t*i
ln Ci/Ti = Cte - Z. t*centrali
Finalmente, también seria:
Además, Beverton e Holt (1957) probaron que:
Reacuérdese
que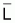 debe calcularse como la
media de los valores de Li ponderados con las abundancias (o sus
índices) o con las capturas.
debe calcularse como la
media de los valores de Li ponderados con las abundancias (o sus
índices) o con las capturas.
Comentarios
1. La aplicación de cualquiera de estos métodos debe venir precedida de la representación gráfica de los dados correspondientes, a fin de verificar si son aceptables o no, las suposiciones de los métodos y, también, para determinar el intervalo adecuado, (ta, tb).
2. Las demostraciones de estas fórmulas son inmediatas (con las indicaciones presentadas), si bien es conveniente desarrollar las demostraciones porque ello permite explicitar las suposiciones que hacen que los métodos sean aplicables.
3. La estimación de Z constante debe intentarse siempre. Incluso cuando no fuere aceptable porque sirve de orientación general sobre la magnitud de los valores que se pueden esperar.
4. Los métodos son citados en la literatura a veces con los nombres de los autores que los aplicaron por primera vez. Por ejemplo, la expresión ln Vi = Cte - Z.t*i es conocida como método de Jones y van Zalinge (1981).
5. La edad media y la talla media en la captura se pueden obtener mediante las siguientes expresiones:
con Ci = captura en número de la edad i
con Ci = captura en número de la clase de talla i
con Ci = captura en número de la clase de edad i
La edad relativa debe ser t* = - (1/K).ln[(L¥- Lt)/(L¥- La)]
FORMULARIO – Estimación del Coeficiente de Mortalidad Total, Z
|
Suposición: Z constante en el intervalo de edades, (ta, tb) |
||||
|
T Constante |
||||
|
|
||||
|
Ti variable |
||||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
Suposición: Z constante en un intervalo de tallas, (La, Lb) |
||||
|
Edad relativa |
||||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
(ecuación de Jones y van Zalinge) |
|||
|
|
|
|||
El método de los mínimos cuadrados (modelo no-lineal) puede ser usado para estimar los parámetros, a y k, de cualquiera de los modelos S-R.
Los valores iniciales del modelo de Beverton y Holt (1957) se pueden obtener rescribiendo la ecuación de la siguiente forma:
(R/S)-1 o
y estimando la regresión lineal simple entre y (= S/R) y x (=S) que dará las estimaciones de 1/(y de 1/(ak). A partir de estos valores se pueden ya estimar los parámetros (a y k) del modelo de Beverton y Holt, que podrán ser considerados como valores iniciales en la aplicación del modelo no-lineal de Beverton y Holt.
En el caso del modelo de Ricker (1954) los parámetros pueden ser obtenidos rescribiendo la ecuación de la siguiente forma:
y estimando la regresión lineal simple entre y (= ln R/S) y x (=S) que dará las estimaciones de ln(y de (-1/k). A partir de estos valores se pueden estimar también los parámetros (a y k) del modelo, que podrán ser considerados como valores iniciales en la aplicación del modelo no-lineal de Ricker.
Antes de aplicar la regresión lineal en cualquiera de estos modelos, es conveniente representar el gráfico de y contra x con el fin de verificar si los puntos marcados se ajustan a una recta.
En los modelos con el parámetro flexible, c, como por ejemplo en el modelo de Deriso (1980), la ecuación podrá escribirse como:
La regresión linear entre y (= (R/S)c) y x (=S) permite estimar los parámetros a y k.
Se puede probar con varios valores de c con el fin de verificar con cual de ellos la recta de y contra x se ajustará mejor, sugiriéndose por ejemplo valores de c entre -1 y 1.
A partir de los valores así obtenidos para a, k y c, los cuales podrán ser considerados como valores iniciales en la aplicación del modelo no-lineal de Deriso, se pueden estimar los parámetros a, k y c del modelo.
7.8.1 ANÁLISIS DE COHORTES CON EDADES – (AC)
El análisis de cohortes es un método que consiste en estimar los coeficientes de mortalidad por pesca, Fi, y el número de supervivientes, Ni, al inicio de cada edad, a partir de las estructuras de las capturas, en número de efectivos, de un stock durante un período de años.
Más concretamente, si tomamos un stock del que se conocen:
Datos
edad, i, siendo i = 1,2,...,k
año, j, siendo j = 1,2,...,n
Matriz de capturas [C] siendo
Ci,j = Captura anual, en número, de los individuos de edad i, durante el año j
Matriz de mortalidad natural [M] siendo
Mi,j = coeficiente de mortalidad natural, a la edad i en el año j.
Vector [T] siendo
Ti = Tamaño del intervalo de edad i (en general, Ti=T=1 año)
Objetivo
estimar
matriz [F]
y
matriz [N].
Es conveniente, para la resolución de este problema considerar por separado las estimaciones correspondientes a: Parte 1, un intervalo de edad i; Parte 2, todas las edades durante la vida de una cohorte y; Parte 3, para todas las edades y años.
PARTE 1 (INTERVALO Ti)
Considérense conocidas las siguientes características de una cohorte, en un intervalo Ti:
Ci = Captura en número
Mi = Coeficiente de mortalidad natural
Ti = Tamaño del intervalo
Si se adopta un valor para el coeficiente Fi entonces es posible estimar el número de supervivientes al inicio, Ni, y al final, Ni+1, del intervalo.
De la expresión:
se puede calcular Ni, que es la única variable de la expresión que es desconocida.
Para calcular Ni+1 se puede utilizar la
expresión 
usando el valor Ni, Fi y Mi calculado anteriormente.
PARTE 2 (DURANTE LA VIDA)
Supongamos ahora que son conocidas las capturas Ci de cada edad i, de una cohorte durante su vida, los valores de Mi y las tallas de los intervalos Ti.
Asumido un valor dado, Fult, para la última clase de edad, es posible, como ya se explicó en la parte 1, estimar todos los parámetros (relacionados con numero de efectivos) para esa última edad. De este modo se conocen el número de supervivientes al inicio y al final de la última edad.
Reacuérdese que el número al inicio de esa última clase de edad, calculado como en el parágrafo anterior, es también el número al final de la clase anterior. De forma que, Nfinal es el número de supervivientes al final de la penúltima clase.
Usando la conocida expresión:
se puede estimar Fi de la clase anterior, que es la única variable desconocida en la expresión.
La estimación puede requerir métodos iterativos de solución aproximada.
Finalmente para estimar Ni el número de supervivientes al inicio de la clase, se puede usar la expresión,
Repitiendo este proceso para todas las clases anteriores, se obtienen sucesivamente, los parámetros para todas las edades, hasta la primera edad. Reacuérdese que Ni es también el número de supervivientes de la clase (i-1) anterior. Cuando la cohorte es completamente pescada, el número al final de la última clase es cero y la captura C debe ser calculada mediante:
Cult =Fult/(Fult+Mi).Nult
Método de Pope
Pope (1972) presentó un método simple que permite estimar el número de supervivientes al inicio de cada edad de la vida de la cohorte a partir de la última edad.
Es suficiente aplicar sucesivamente y de atrás hacia delante la expresión:
Ni » (Ni+1 e MT/2 + Ci).e MT/2
Pope indica que la aproximación es buena cuando MT £ 0.6
La expresión puede derivarse, según Pope, suponiendo que la captura se efectúa exactamente en el punto central del intervalo Ti (Figura 7.3).

|
Figura 7.3 |
Evolución del número de supervivientes durante Ti con la captura realizada en el punto central del intervalo |
Procediendo del fin al principio sucesivamente obtendremos:
N’’ =Ni+1.e +MTi/2
N’=N’’ + Ci
Ni=N’.e+MT/2
substituyendo N’ por N’’+Ci, resulta:
Ni= (N’’+ Ci). e +MT/2
y, substituyendo N’’ por Ni+1.e +MTi/2, tenemos:
Ni » (Ni+1.e+MT/2 + Ci).e +MT/2
Parte 3 (período de años)
Supongamos, finalmente, que son conocidas, durante un período de años, la matriz de captura [C], la matriz de mortalidad natural [M] y el vector tamaño de los intervalos [T], en que las filas, i, son edades y las columnas, j, son años.
Admitamos también la adopción de valores de F para últimas edades de todos los años representados en las matrices y los valores de F de todas las edades en el último año.
Llamando a estos valores Fterminais (Figura 7.4)
|
Años |
|
||||
|
Edades |
2000 |
2001 |
2002 |
2003 |
|
|
1 |
C |
C |
C |
C |
Fterminal |
|
2 |
C |
C |
C |
C |
Fterminal |
|
3 |
C |
C |
C |
C |
Fterminal |
| |
Fterminal |
Fterminal |
Fterminal |
Fterminal |
|
|
Figura 7.4 |
Matriz captura, [C], con Fterminal en la última fila y en la última columna de la matriz C. El sombreado indica las capturas de una cohorte |
Cabe señalar que en estas matrices los elementos en diagonal corresponden a los valores de una misma cohorte, dado que a un elemento de una edad y de un año le sigue, en diagonal, el elemento con 1 año mas de edad y del año siguiente, y, por tanto, el elemento siguiente de la cohorte.
Por lo dicho en las partes 1 y 2 es posible estimar Fs y Ns sucesivamente para todas las cohortes presentes en la matriz de captura.
Comentarios
1. Muchas veces, en la práctica, se adoptan valores Mi,j constantes y iguales a M.
2. Cuando los datos se refieren a edades, los valores Ti acostumbran a ser todos iguales a 1 año.
3. Los últimos grupos de cada año son a veces edades (+). Las capturas correspondientes están constituidas por individuos pescados durante esos años, con aquella edad o superior. Así, los valores acumulados no pertenecen a la misma cohorte, pero son supervivientes de varias cohortes anteriores. No seria legítimo usar la captura de un grupo (+) para analizar la cohorte en cuestión, porque diferentes cohortes resultan de reclutamientos de fuerzas diversas. A pesar de ello, el grupo (+) es importante para el cálculo de los totales anuales de captura en peso, Y, y de biomasas, totales, B, y reproductora, BD. Así, se acostumbra a realizar el análisis de cohortes a partir de la edad inmediatamente anterior al grupo (+) y a utilizar el grupo (+) solo para los cálculos de Y, B y BD. El valor de F en ese grupo (+) para cada año se puede estimar considerándolo el mismo coeficiente de mortalidad por pesca de la edad anterior o, en algunos casos, un valor razonable en relación a los valores de Fi en el año en cuestión.
4. Una dificultad en la aplicación de la técnica AC surge cuando el número de edades es pequeño o cuando los años son pocos. En efecto en tales casos las cohortes tienen pocas clases de edad representadas en la Matriz [C] y las estimaciones serán muy dependientes de los valores adoptados de Fterminal.
5. El análisis de cohortes (AC) también es llamado: VPA (Virtual Population Analysis), método de Derzhavin, método de Murphy, método de Gulland, método de Pope, Análisis Sequencial, etc. A veces es llamado AC cuando se usa la fórmula de Pope y VPA en otros casos. Megrey (1989) llevo a cabo una revisión muy completa sobre el análisis de cohortes.
6. También es posible estimar los restantes parámetros para una edad i, relacionados con número de efectivos, o sea, Ncumi,
, Di, Zi y Ei. Con información sobre pesos individuales iniciales o medios, matriz [w] o matriz [
], también se pueden calcular las capturas anuales en peso [Y], las biomasas al inicio de los años, [B] y las biomasas medias durante los años [
]. Con información sobre ojivas de madurez en cada año, por ejemplo, al inicio del año, se pueden también calcular las biomasas reproductoras, [BD]. Normalmente solo se estiman las capturas totales Y, las biomasas del stock (totales y reproductoras) al inicio y las biomasas medias del stock (totales y reproductores) para cada año.
7. Los elementos de la primera fila de la matriz [N] pueden considerarse estimaciones de reclutamiento a la pesca para cada año.
8. El hecho de haber adoptado Fterminales y que estos valores influencien los resultados – matriz [F] y matriz [N] – obliga a seleccionar valores de Fterminales próximos a los verdaderos. La coherencia entre las estimaciones de los parámetros mencionados en los puntos 6 y 7 y otros datos o índices independientes (por ejemplo, estimaciones por métodos acústicos de reclutamiento o biomasas, estimaciones de índices de abundancia o cpue’s, de esfuerzos de pesca, etc.) debe ser analizada. Estas verificaciones son obligatorias para validar el análisis de cohortes (a veces se usan incorrectamente los conceptos calibración o sintonización, expresiones que pretenden traducir el termino inglés «tuning», en vez de validación).
9. La hipótesis que establece que el patrón de explotación es constante de año en año, significa que el nível de pesca de cada año y el patrón relativo de explotación de cada edad pueden separarse en el producto Fj.si, o sea, Fi,j = Fj.si, siendo i = edad y j = año. Esta hipótesis puede ser verificada utilizando la matriz [F] obtenida en el analisis de cohortes.
Se acostumbra a llamar a esta separación VPA-Separable (SPVA).
Si
y
y
De este modo, si Fij = Fjsi se puede probar que
Si los valores estimados para Fi,j son iguales a los valores anteriores, llamados Fsepij = Fj.si, entonces la hipótesis esta verificada. Esta comparación puede ser realizada de varias maneras, si bien la mas simple y mas rápida, probablemente sea calcular los cocientes (Fsepij/Fij) que, en el caso de que la hipótesis sea verdadera deberán ser iguales a 1. Si la hipótesis no es verificada siempre será posible considerar otras hipótesis, como que el vector anual [s] sea constante algunos años, sobre todo en los años recientes.
10. En cualquier caso, se acostumbra a considerar un intervalo de edades, en el que se supone que los individuos capturados están «completamente reclutados». Si el intervalo de edades corresponde a individuos completamente reclutados seria de esperar que el patrón relativo de exploración calculado se aproximase de 1 (para las restantes edades no completamente reclutadas el patrón relativo de exploración debería ser menor que 1). Entonces se calcula, para el intervalo de edad, i, la media de los valores de Fi,j en cada año. Esas medias,
, son consideradas como los niveles de pesca en los años respectivos. Entonces, el patrón relativo de exploración en cada celda, seria el cociente Fi,j /
.
7.8.2 ANÁLISIS DE COHORTES CON TALLAS – (LCA)
La técnica del análisis de cohortes, aplicada a la estructura de las capturas de una cohorte durante su vida puede ser efectuada con intervalos de tempo, Ti, no constantes. Esto significa que si se dispone de la estructura de las capturas de una cohorte durante su vida, por clases de talla, también se puede «analizar la cohorte».
Los métodos utilizados para el análisis de cohortes en estas circunstancias se denominan LCA («Length Cohort Análisis» en inglés). Las mismas técnicas, método de Pope, método iterativo, etc., del AC por edades, pueden ser aplicadas en el análisis LCA (reacuérdese que los intervalos Ti’s pueden ser calculados a partir de edades relativas).
Un modo de aplicar el LCA a la composición de las capturas, por talla, será: agrupar, previamente, las capturas cuyas clases de talla pertenezcan a un mismo intervalo de edad, obteniendo así la composición de las capturas por edades. La técnica AC puede entonces ser aplicada directamente a la matriz [C]. Esta técnica es conocida por «cortar en capas», (slicing en inglés) la composición por tallas. Para «cortar en capas» una distribución por tallas se acostumbra a invertir la ecuación de crecimiento en talla de von Bertalanffy y estimar la edad ti para cada talla Li (a veces se usan edades relativas t*i) (Figura 7.5). Entonces, la captura de un determinado grupo de edad i se obtiene agrupando las capturas observadas en las clases de talla comprendidas entre las dos edades extremas del respectivo intervalo de edades. Puede suceder que haya clases de talla que estén constituidas por elementos que pertenezcan a dos grupos de edad consecutivos. En estos casos será necesario repartir la captura de esas clases extremas en dos partes y atribuirlas a cada una de esas edades. En el ejemplo de la Figura 7.5, las capturas de la clase de tallas (24–26) pertenecen a la edad 0 y a la edad 1. De modo que, es necesario repartir esa captura entre las dos edades. Un método simple consiste en atribuir a la edad 0 la fracción (1.00 - 0.98)/(1.06 - 0.98) = 0.25 y a la edad 1 la fracción (1.06 - 1.00)/(1.06 - 0.98) = 0.75 de la captura anual de esa clase de tallas. El método no es el más apropiado, puesto que se basa en la suposición de que en las clases de talla la distribución de los ejemplares por talla es uniforme. Por eso, cuando se aplica esta técnica de repartición, es conveniente usar el menor intervalo de clase posible.
Otro modo de realizar el análisis de cohortes con tallas, consiste en no agrupar las capturas por clases de talla comprendidas en el mismo grupo de edad, sino usarlas separadamente. Las cohortes pueden ser seguidas en la matriz [C], a través de las clases de tallas pertenecientes a una misma edad, en un determinado año, con las clases de talla de la edad siguiente, en el año siguiente, etc. De este modo las diferentes cohortes existentes en la matriz serán separadas y la evolución de cada una de ellas será visible, no por edades, pero si por clases de talla (ver Figura 7.5).
|
Grupo |
|
|
Años |
|||
|
Edad |
Edad relativa |
Clases |
2000 |
2001 |
2002 |
2003 |
|
|
1.03 |
20- |
41 |
30 |
17 |
49 |
|
0 |
1.54 |
22- |
400 |
292 |
166 |
472 |
|
|
1.98 |
24- |
952 |
699 |
400 |
1127 |
|
|
2.06 |
26- |
1766 |
1317 |
757 |
2108 |
|
1 |
2.30 |
28- |
2222 |
1702 |
985 |
2688 |
|
|
2.74 |
30- |
2357 |
1872 |
1093 |
2902 |
|
|
2.88 |
32- |
2175 |
1091 |
1067 |
2739 |
|
|
3.00 |
34- |
1817 |
948 |
1416 |
1445 |
|
|
3.42 |
36- |
1529 |
812 |
1270 |
1250 |
|
2 |
3.64 |
38- |
1251 |
684 |
980 |
1053 |
|
|
3.83 |
40- |
1003 |
560 |
702 |
710 |
|
|
3.96 |
42- |
787 |
290 |
310 |
558 |
|
3 |
4.01 |
44- |
595 |
226 |
179 |
834 |
|
|
4.25 |
46- |
168 |
70 |
71 |
112 |
|
|
|
|
|
|
|
Cohorte del año 2000 |
|
Figura 7.5 |
Ejemplo de una matriz [C] con clases de talla, «cortadas en capas» (slicing), destacando en negrita la evolución de una cohorte |
Se puede aplicar el método LCA de Jones (1961), para analizar una composición de tallas durante la vida de una cohorte. Este método analiza una cohorte durante la vida, constituida por las capturas en clases de talla aplicando los métodos ya estudiados de AC con Ti no-constantes. Los valores de Ti son calculados como Ti = ti+1*-ti*, donde ti* y ti+1* son las edades relativas correspondientes a los extremos del intervalo de talla i. El vector [N] obtenido estará constituido por el número de supervivientes iniciales en cada clase de talla de la cohorte y no en cada clase de edad.
Comentarios
1. Ciertos modelos, denominados modelos integrados, consideran toda la información disponible (capturas, datos de campañas científicas, datos de esfuerzo, de rendimiento, etc.) que, juntamente con la matriz [C], son integrados en un único modelo para optimizar la función criterio definida previamente.
2. Fry (1949) consideró las capturas por edades acumuladas, del final al principio de una cohorte durante la vida, como imagen virtual del número de supervivientes al inicio de cada edad (a lo que el autor llamo «población virtual»);
En la pesquería estudiada por Fry, M era prácticamente nula. Pero si M es diferente de cero se puede decir que el número Ni de supervivientes al inicio del intervalo i será:
donde Dk representa el número total de muertos en el intervalo k.
Adoptando para las tasas de explotación, E, los valores iniciales, Ek(0), en todas las clases, se calcula Dk(0) = Ck/Ek(0).
Ni(0) puede ser calculado como los valores acumulados de muertos totales, es decir:
Entonces resulta:
y se puede calcular:
Los nuevos valores de E serán:
Comparando Ei(1) con Ei(0) se pueden estimar, de un modo semejante al descrito para los métodos iterativos, los valores de E con la aproximación deseada.
Reacuérdese que, en la última clase el número, Nult, es igual al número de muertos, Dult, y puede ser calculado como:
3. Finalmente se llama la atención de que los resultados del AC y del LCA nos dan una perspectiva de la historia del stock en los años anteriores. Esa información es, como se vio anteriormente, útil para la realización de las proyecciones a Corto y Largo Plazo. Normalmente en el año en que se realiza la evaluación todavía no están disponibles los datos de capturas de ese año, por lo que han de proyectarse las capturas y biomasas para el año actual antes de efectuar la proyección a Corto Plazo.
4. Cuando se calculan edades relativas, se acostumbra, por una cuestión de uniformidad, a adoptar la edad inicial ta igual a cero. El valor de La correspondiente será entonces el límite inferior de la primera clase de tallas representada en las capturas.