1. Calcular:
|
a) |
|
|
|
|
||||
|
b) |
|
|
|
|
||||
|
c) |
|
|
|
|
||||
|
d) |
|
|
|
|
||||
|
e) |
|
|
|
|
|
|
|
|
2. Verificar que
|
a)
|
b)
|
|
c) |
d) |
3. Desarrollar las siguientes expresiones aplicando logaritmos (naturales) a ambos miembros de la igualdad:
|
a)
|
b)
|
c)
|
Nota: a, b, y c son constantes; e
es la constante neperiana 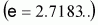 ;
x e y son variables.
;
x e y son variables.
4. Determinar el valor de x en las siguientes expresiones:
|
a)
|
b)
|
c)
|
5. Calcular las derivadas de las expresiones siguientes:
|
a) y=13 |
g) y=5x |
m) y=(4+2.x)3 |
|
b) y=3-8.x |
h) y=y-3.x |
n) y=(x-6)2 |
|
c) y=x5 |
i) y=ln x |
o) y= a.(3-y-b.x)3 |
|
d) y=x2/7 |
j) y=ln(5.x+4) |
p) y= (4.x+3).(ex-4) |
|
e) y=x-3 |
k) y= 1/x |
|
|
f) y=e3.x |
l) y= (2+4.x)/(3-x) |
|
6. Calcular las Primitivas (integrales indefinidas) de las siguientes funciones:
|
a)
|
f)
|
k)
|
|
b)
|
g)
|
l)
|
|
c)
|
h)
|
m)
|
|
d)
|
i)
|
n)
|
|
e)
|
j)
|
o)
|
7. Calcular el área abarcada por la función
a)
entre
y
b)
entre
y
c)
entre
y
d)
entre
y
8. Calcular el valor de
 para
para
a)
entre
y
b)
entre
y
c)
entre
y
9. Calcular el Valor Medio de y para
a)
entre
y
b)
entre
y
c)
entre
y
10. Calcular la integral de
a)
con la condición inicial
donde
b)
con la condición inicial
c)
con la condición inicial
d)
con la condición inicial