8.25 Estimación de Z

(7.7)

GRUPO I

Una campaña de arrastre por el método de área barrida permitió a los científicos del Instituto de Investigación Marina de Bergen, en Noruega, estimar la abundancia de las distintas clases de edad del stock de bacalao, Gadus morhua, en enero de 1995 (tabla siguiente).

1. Representar gráficamente los logaritmos de los números de supervivientes contra la edad.

2. Decir a partir de que edad se puede considerar que el coeficiente de mortalidad total Z del stock es constante.

3. Estimar el coeficiente de mortalidad total Z del stock en enero de 1995.

GRUPO II

La tabla siguiente muestra las capturas medias, en número, por edad da solla, Pleuronectes platessa, realizadas por cada 100 horas de arrastre en dos períodos, 1929–1938 y 1950–1958.

1. Estimar el coeficiente de mortalidad total Z del stock en cada uno de estos dos períodos.

2. Considerando que el esfuerzo de pesca medio ejercido sobre la solla del Mar del Norte durante los dos períodos fue de 5 millones de horas de arrastre en 1929–1938 y de 3.1 millones de horas de arrastre en 1950–1958. Estimar en cada período:

a) el coeficiente de mortalidad natural M;

b) el coeficiente de capturabilidad q;

c) el coeficiente de mortalidad por pesca F.

GRUPO III

A continuación se presenta, para un determinado recurso, la composición anual de las capturas por edades de 1988 a 1994, en millones de individuos.

CAPTURAS (millones de individuos)

1. Calcular la composición anual media de 1988–1994.

2. Estimar Z a partir de esa composición media.

3. Estimar Z a partir de la edad media en la composición media de la captura.

4. Estimar Z para cada año del período dado.

5. Comparar las Zs anuales con las Zs obtenidas en las cuestiones 2 y 3.

GRUPO IV

A continuación se presenta la composición por talla, en equilibrio, de un determinado recurso, con cm y K = 0.2 año^-1.

1. Calcular las edades relativas correspondientes al límite inferior de cada clase de talla.

2. Determinar el intervalo de edad correspondiente a cada clase de talla.

3. ¿A partir de que clase se puede considerar Z constante?

4. Determinar Z utilizando:

a) Las capturas de cada clase.

b) Las capturas acumuladas.

c) La talla media en la captura.

5. Comparar los valores de Z obtenidos por los diferentes métodos.

GRUPO V

Para un determinado recurso pesquero se conoce la composición por talla de las capturas en tres períodos de tiempo distintos.

Considerar la clase de talla de 45 cm como la primera clase completamente reclutada.

Adoptar K = 0.3 año^-1 y 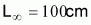como los parámetros de crecimiento de von Bertalanffy para este recurso.

1. Estimar los valores de coeficiente de mortalidad total Z para cada período y comentar los resultados.