(7.9.1)
GRUPO I
1. Consideremos un intervalo de tiempo i,
 . Se sabe que en este
intervalo de tiempo:
. Se sabe que en este
intervalo de tiempo:
Mi = 0.4 año-1
Ti = 2.3 año
Ci = 230 millones de individuos
a) Adoptar el valor 0.5 año-1 para el coeficiente de mortalidad por pesca durante el intervalo i y calcular el número de supervivientes al final del intervalo y el número de supervivientes al inicio del intervalo.
2. Considerando igualmente el intervalo de tiempo i,
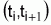 , pero siendo en este
intervalo de tiempo:
, pero siendo en este
intervalo de tiempo:
Mi = 0.6 año-1
Ti = 0.9 año
Ci = 98 millones de individuos
a) Calcular el valor del coeficiente de mortalidad por pesca Fi durante el intervalo i, sabiendo que el número Ni de supervivientes al inicio del intervalo, i, es igual a 172 millones de individuos.
3. Considerando de nuevo el intervalo de tiempo (ti, t I+1), y sabiendo que en ese intervalo de tiempo:
Mi= 0.5 año-1
Ti = 1 año
Ci = 42 millones de individuos
a) Calcular el valor del coeficiente de mortalidad por pesca, durante el intervalo i, sabiendo que el número de supervivientes al final del año fue Ni+1= 85 millones de individuos. Calcular el valor de Fi utilizando la fórmula de Pope.
GRUPO II
Los datos de la tabla siguiente se refieren a las capturas en número (millones) de una cohorte de merluza, Merluccius merluccius, en las aguas atlánticas de la Península Ibérica.
|
Edad (años) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Ci (millones) |
712 |
3941 |
8191 |
10311 |
5515 |
4149 |
3081 |
1185 |
549 |
Adoptar un valor de 0.2 año-1 para el coeficiente de mortalidad natural, constante para todas las edades.
1. Supongamos que el valor del coeficiente de mortalidad por pesca en la última edad (8 años) fue de 1.0 año-1. Calcular, por el método iterativo y por el método de Pope y para cada edad de la cohorte:
a) El valor del coeficiente de mortalidad por pesca.
b) El número de supervivientes al inicio de la edad.
c) Comparar los resultados obtenidos por los dos métodos.
d) Representar gráficamente los valores de Fi estimados contra la edad, y decir cual fue el reclutamiento de esta cohorte a la fase explotada.
GRUPO III
1. Con el objeto de analizar la influencia de la Fterminal utilizada, repetir los cálculos del apartado anterior, usando uno de los métodos anteriores, utilizando 0.3 y 1.5 año-1 para el valor de Fterminal.
a) Representar gráficamente los valores estimados de Fi y Ni contra a edad.
b) Comentar las diferencias entre los gráficos para los diferentes valores de Fterminal.
2. Con el objeto de analizar la influencia de la M utilizada, repetir los cálculos del apartado 1, usando uno de los dos métodos anteriores, utilizando valores de M de 0.1 y 0.4 año-1.
a) Representar gráficamente los valores estimados de Fi y Ni contra a edad.
b) Comentar las diferencias entre los gráficos para los diferentes valores de M.
GRUPO IV
Las capturas anuales por clase de edad de un determinado recurso, para los años 1985 a 1994, se muestran en la tabla siguiente.
|
Capturas por clase de edad (Millones de individuos) |
||||||||||
|
Años |
||||||||||
|
Edad |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
1993 |
1994 |
|
0 |
67 |
88 |
104 |
290 |
132 |
90 |
63 |
38 |
52 |
90 |
|
1 |
532 |
1908 |
1841 |
1671 |
4172 |
1915 |
1284 |
906 |
541 |
704 |
|
2 |
2070 |
1756 |
4424 |
3178 |
2534 |
6320 |
2826 |
1911 |
1322 |
741 |
|
3 |
728 |
4016 |
2256 |
4042 |
2499 |
1972 |
4742 |
2115 |
1382 |
890 |
|
4 |
353 |
945 |
3309 |
1273 |
1926 |
1170 |
883 |
2102 |
896 |
540 |
|
5 |
97 |
439 |
733 |
1730 |
558 |
827 |
479 |
356 |
807 |
316 |
|
6 |
16 |
107 |
300 |
333 |
656 |
207 |
291 |
166 |
117 |
243 |
|
7 |
25 |
8 |
73 |
136 |
126 |
243 |
73 |
101 |
54 |
35 |
|
8 |
5 |
7 |
5 |
33 |
52 |
47 |
85 |
25 |
33 |
16 |
El modo de operar de la flota de pesca se mantuvo constante durante el período, pero el número de embarcaciones aumento significativamente. Actualmente, se considera que el recurso se encuentra intensamente explotado.
Además de la información sobre la pesquería, se dispone también de estimaciones de los parámetros de crecimiento en peso de este recurso y del coeficiente de mortalidad natural:
|
L¥= 38.5 cm |
a = 0.021 de la relación W(g)- L(cm) |
|
K = 0.25 año-1 |
b = 2.784 de la relación W(g)- L(cm) |
|
to = - 0.51 año |
M = 0.3 año-1 |
1. Estimar el coeficiente de mortalidad por pesca y el número de supervivientes al inicio del año para cada clase de edad y para cada año. Utilizar el método de Análisis de Cohortes de Pope.
a) En el primer ensayo seleccionar Fterminal = 0.5 año-1 para la última edad en todos los años y para todas las edades en el último año de la matriz.
b) Analizando la matriz F obtenida en a) seleccionar nuevos valores de Fterminal y repetir la aplicación del método de Pope.
2. Además de la información facilitada en el apartado anterior se sabe que la puesta tiene lugar en un período concreto, próximo al principio del año. Se realizaron campañas de evaluación por métodos acústicos, en la época de puesta, para estimar la biomasa reproductora (kg/hora de arrastre). Los resultados obtenidos se muestran en la tabla siguiente:
|
Años |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
1993 |
1994 |
|
Índice de biomasa reproductora |
1270 |
1613 |
1629 |
1424 |
1300 |
1209 |
1000 |
718 |
476 |
326 |
La información biológica recogida durante las campañas fue también usada para estimar la ojiva de madurez del stock en la época de puesta:
|
Edad (años) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
% Maduros |
0 |
1 |
20 |
50 |
80 |
100 |
100 |
100 |
100 |
a) Calcular la biomasa reproductora en la época de puesta en cada año del período 1985–1994 utilizando los resultados del Análisis de Cohortes realizado.
b) Utilizar la información de las campañas acústicas para validar (o no) el Análisis de Cohortes.
c) Comentar la validación.