4.1.1 EVOLUTION DE LA STRUCTURE PAR AGES
Considérez l’évolution d’un stock constitué par plusieurs cohortes, pendant un an. La Figure 4.1 illustre la structure du stock au début de l’année, les caractéristiques moyennes pendant l’année et la structure qui survit à la fin de l’année.
Figure 4.1 Structure du stock au début et à la fin de l’année

Représentant par i = 1,2,3,... les âges.
4.1.2 CARACTERISTIQUES DU STOCK AU DEBUT DE L’ANNEE
Soient:
Ni - l’effectif d’âge i, au début de l’année.
wi - le poids individuel de l’âge i, au début de l’année.
Bi - la biomasse totale des individus d’âge i, au début de l’année.
N - l’effectif des survivants du stock au début de l’année.
B - la biomasse totale du stock au début de la même année.
Alors, on aura:
4.1.3 CARACTERISTIQUES DU STOCK PENDANT L’ANNEE
Soient:
|
Mi, Fi et Zi |
coefficients de mortalité naturelle, par pêche et totale à l’âge i pendant l’année |
|
|
poids moyen individuel de l’âge i pendant l’année |
|
|
effectif moyen des individus pendant l’année |
|
|
biomasse moyenne des individus pendant l’année |
|
|
capture, en nombre, pendant l’année |
|
|
capture, en poids, pendant l’année |
|
|
poids individuel moyen des individus capturés pendant l’année |
|
|
poids individuel moyen des individus du stock pendant l’année |
Alors:
avec Ncumi, Ci, Bcumi et Yi calculés pour tous les âges i selon les expressions données antérieurement dans le Chapitre 3 - Cohorte.
4.1.4 CARACTERISTIQUES DU STOCK A LA FIN DE L’ANNEE
L’effectif d’âge i+1 sera:
Soit:
R - recrutement de la cohorte l’année suivante
Alors l’effectif et la biomasse du stock au début de l’année suivante seront:
où R.W1 est la biomasse du recrutement de l’année suivante.
Commentaires
1. La fin de l’année coïncide avec le début de l’année suivante. Ainsi le nombre de survivants d’âge i à la fin de l’année sera Ni+1.
2. La somme du nombre total de survivants du stock à la fin de l’année n’est pas égale à l’effectif du stock au début de l’année suivante puisqu’il manque les recrues qui sont entrés pendant l’année.
3. Le nombre total de morts, D, pendant
l’année, serait

4. Comme l’intervalle de temps est d’un an, les valeurs accumulées seront égales aux valeurs moyennes, soit:
5. L’utilisation des mêmes symboles N, B, D, etc., pour le stock et la cohorte ne devra pas prêter à confusion.
4.2.1 NIVEAU DE PECHE ET REGIME D’EXPLOITATION
L’action directe de l’homme dans la pêche d’un stock se traduit par l’influence des coefficients Fi de mortalité par pêche, qui sont associés à la quantité d’effort et à la disponibilité des individus de différentes longueurs ou âges, i, aux engins de pêche utilisés par les navires pendant l’année.
Il est coutume de séparer les coefficients de
mortalité par pêche en deux composants: un dénommé
niveau d’intensité de mortalité par pêche,
 , pendant
l’année, ou, plus simplement, niveau de pêche, F. Le niveau
est associé à la quantité d’effort de
pêche, c’est-à-dire au nombre de navires qui
pêchent, au nombre de jours, de prises, d’heures de pêche
pendant l’année, à l’efficacité ou à la
puissance de pêche des navires ou engins de pêche et une autre
composante, dénommée régime d’exploitation,
si, qui est associé aux propriétés
sélectives des engins de pêche par rapport aux longueurs ou
âges des individus disponibles à la capture, au cours de cette
année.
, pendant
l’année, ou, plus simplement, niveau de pêche, F. Le niveau
est associé à la quantité d’effort de
pêche, c’est-à-dire au nombre de navires qui
pêchent, au nombre de jours, de prises, d’heures de pêche
pendant l’année, à l’efficacité ou à la
puissance de pêche des navires ou engins de pêche et une autre
composante, dénommée régime d’exploitation,
si, qui est associé aux propriétés
sélectives des engins de pêche par rapport aux longueurs ou
âges des individus disponibles à la capture, au cours de cette
année.
On désigne par régime de pêche l’ensemble conjugué du niveau de pêche (valeur unique pour tous les âges) et du régime d’exploitation (valeurs différentes selon la longueur ou âge) pendant un an. La désignation régime de pêche peut causer quelque confusion avec le régime d’exploitation de même que la désignation de régime de pêche peut causer quelque confusion avec ce que les économistes et administrateurs désignent par régime de pêche.
On peut dire que le régime de pêche,
Fi, pendant un an et correspondant à un âge i, est
égal au produit du niveau de pêche de cette année,
 , par le régime
d’exploitation de chaque âge, si,
c'est-à-dire:
, par le régime
d’exploitation de chaque âge, si,
c'est-à-dire:
Les analyses des effets du coefficient de mortalité par pêche, Fi, sur les caractéristiques de la ressource et des captures, influencent normalement le niveau de pêche, si l'on tient compte du fait que le régime d’exploitation se maintient stable. Parfois (comme par exemple quand il y a des changements dans la taille de la maille du filet de pêche) on peut analyser les effets de changements du régime d’exploitation en maintenant fixe le niveau de pêche, mais rien n’empêche que les effets conjugués des deux composants soient analysés.
Dans la mesure où il n’y a pas de doutes, le
niveau de pêche,  , est
représenté simplement par F.
, est
représenté simplement par F.
Quand on connaît la structure du stock au début
d’une année, on peut, comme on l’a déjà vu,
projeter les caractéristiques du stock au cours de cette année et
estimer la structure du stock au début de l’année suivante
(avec l’exception du recrutement de cette année), pour
différentes valeurs du niveau de pêche,
 , et du régime
d’exploitation, si, qui seront appliquées pendant
l’année.
, et du régime
d’exploitation, si, qui seront appliquées pendant
l’année.
Il est donc nécessaire de connaître les paramètres biologiques de croissance, de maturation et la mortalité naturelle à chaque âge pendant l’année.
En adoptant une valeur pour le recrutement de l’année suivante, la prévision sera possible pour une autre année et ainsi de suite. Le plus grand inconvénient dans la prévision du stock pour plusieurs années est que ces prévisions dépendent chaque fois plus des valeurs de recrutement annuel adoptées. Par conséquent, dans la pratique, la prévision se fera pour un an, ou tout au plus, pour deux ans.
Notez que pour projeter un stock pour l’année suivante il faut disposer de données relatives à l’année antérieure. Ainsi, le premier pas consiste à projeter le stock pour l’année en cours (en déterminant ses caractéristiques à la fin de l’année) et ensuite à projeter la capture et la biomasse pour l’année suivante.
On suppose par exemple qu’en 1997 on prétendait projeter les caractéristiques du stock pour 1998. Comme les données disponibles sont, dans la meilleure des hypothèses, celles de 1996, il faudra en premier lieu projeter le stock de 1996 au début de l’année 1997 et, seulement après, réaliser les prévisions pour 1998, en estimant au préalable le recrutement de 1998.
On considère le vecteur N de composants N1, N2,..., Ni,... comme représentant la structure du stock au début d’une année. Notez que 1,2,...,i,... désignent les âges des survivants de chaque cohorte présente au stock, au début de l’année.
Mi et Fi représentent les coefficients de mortalité naturelle et par pêche de l’âge i, qui sont supposés constants pour les années à venir.
La Figure 4.2, illustre à l’aide d’un stock théorique, les prévisions de l’effectif des survivants des différentes cohortes présentes au début de l’année 1980, pendant les années futures de 1981-1986 (les valeurs sont en millions d’individus).
On remarque qu’il manque les recrutements qui n’ont pas encore eu lieu mais qui entreront dans la zone de pêche de 1981 à 1986. Il est donc clair qu’il manque aussi les survivants respectifs, pendant la même période.
On suppose maintenant que les recrutements de ces années étaient égaux à celui de 1980, soit, 440 millions d’individus. La Figure 4.3 montre les prévisions dans les années futures. On peut voir que les valeurs correspondantes aux même âges, de la structure du stock en 1986 et de l’évolution de la cohorte de 1980, sont égales.
Figure 4.2 Structure du stock au début de 1980 et prévisions de l’effectif des survivants (millions d’individus) des différentes cohortes présentes au début des années 1981-1986

Figure 4.3 Prévisions à long terme de la cohorte de 1980 et structure du stock en fixant un recrutement annuel constant de 440 millions d’individus

Une conclusion pratique pour obtenir la structure du stock en 1986 (à LT) serait de suivre l’évolution de la cohorte de 1980 et, donc, il ne serait pas nécessaire d’avoir la structure complète du stock au début de l’année. Il suffit de fixer une valeur pour le recrutement (R) d’une cohorte (et, bien sûr, supposer stables les paramètres biologiques des années suivantes). Un conseil: les calculs devront être réalisés en fixant un Recrutement de 1000 individus (avec un logiciel on fixe un recrutement égal à 1).
Les caractéristiques du stock à LT dans les conditions antérieures sont, généralement, proportionnelles au Recrutement (exception faite des valeurs moyennes - âge moyen, longueur moyenne, poids moyen à la capture, etc., qui sont indépendantes de la valeur de R). Ainsi, ces prévisions à LT sont aussi nommées prévisions par recrue et prévisions «d’équilibre» ou prévisions à LT.
Les prévisions à LT ne se limitent pas aux
survivants au début de l’année, elles s’étendent
aussi aux valeurs des abondances moyennes,
 , pendant
l’année et aux captures en nombre, Ci.
, pendant
l’année et aux captures en nombre, Ci.
Connaissant les poids individuels initiaux, Wi et
moyens,  , des
âges i, et d’autres paramètres comme ceux de la
maturation, on peut aussi projeter les biomasses totales, B ou B, et les
biomasses de ponte, BD ou
, des
âges i, et d’autres paramètres comme ceux de la
maturation, on peut aussi projeter les biomasses totales, B ou B, et les
biomasses de ponte, BD ou  ,
de même que les captures en poids, Y.
,
de même que les captures en poids, Y.
Pour effectuer les calculs des prévisions à LT
il importe de vérifier si les valeurs accumulées, Ncumi
et Bcumi, d’une cohorte pendant un an sont égales aux
valeurs moyennes,  et
et
 , pendant cette
année. Ainsi, les caractéristiques principales du stock, pendant 1
an et à LT, peuvent être calculée comme:
, pendant cette
année. Ainsi, les caractéristiques principales du stock, pendant 1
an et à LT, peuvent être calculée comme:
C = S Ci
Y = S Yi
Diverses prévisions à LT peuvent être
réalisées avec différentes valeurs de Fi, ou
mieux encore, avec divers niveaux de pêche,
 , ou divers
régimes d’exploitation, si.
, ou divers
régimes d’exploitation, si.
Pour les analyses sur l’influence du niveau de pêche dans les captures et le stock, il est coutume de maintenir fixe le régime d’exploitation. Mais si on prétend évaluer les conséquences dans le stock et dans la capture d’une “correction” du régime d’exploitation (changement de maille, par exemple), on maintient fixe le niveau de pêche et on essaye différentes valeurs de si. On peut aussi projeter les stocks en faisant varier simultanément les deux composantes du régime de pêche.
La Figure 4.4 (A-C) illustre divers types de courbes à LT des Production par Recrue, en maintenant fixe le régime d’exploitation. Pour d’autres régimes d’exploitation, les courbes peuvent être différentes.
Figure 4.4 Exemples de formes des courbes de la Production par Recrue (Y/R) contre F, selon un régime d’exploitation donné: (A - avec maximum, B - aplatie, C - asymptotique)
Figure A

Figure B

Figure C

La Figure 4.5 (A-E) illustre les relations entre les caractéristiques les plus importantes du stock et le niveau de pêche, en maintenant stable le régime d’exploitation.
Figure 4.5 Relation entre les caractéristiques du stock à long terme contre le niveau de pêche F, (A - nombre moyen/R, B - capture en nombre/R, C - poids moyen à la capture, D - biomasse moyenne/R, E - capture en poids/R)
Figure A

Figure B

Figure C

Figure D

Figure E

Une analyse plus détaillée de ces courbes sera présentée ultérieurement au chapitre 5.
Conclusion
|
La structure par âges du stock à LT pendant 1 an |
= |
Évolution de la cohorte pendant sa vie |
Commentaires
1. Pour projeter un stock pendant un an à LT, en supposant constants les recrutements annuels, on projette une cohorte pendant toute sa vie.
2. Il faut connaître Mi pour tous les
âges de la cohorte, de même que Wi,
 , si et le niveau
de pêche,
, si et le niveau
de pêche,  , qui est
supposé constant dans les années à venir.
, qui est
supposé constant dans les années à venir.
3. Le recrutement peut être n’importe lequel. On adopte R = 1000 ou R = 1 (avec les feuilles de calculs de l’ordinateur).
4. Les 5 caractéristiques du stock les plus
importantes sont  ,
,
 , Cman,
Yman et
, Cman,
Yman et
 (voir les
premières pages de ce chapitre pour les expressions de calcul
respectives).
(voir les
premières pages de ce chapitre pour les expressions de calcul
respectives).
5. Une autre caractéristique importante du stock est la biomasse de ponte, BP. Pour effectuer son calcul il faut connaître l’ogive (ou l’histogramme) de maturation.
6. Les prévisions à LT sont aussi désignées comme situations d’équilibre.
7. Les prévisions à LT servent à définir des objectifs de gestion à LT, ou buts à atteindre.
8.  annuel
est le même quel que soit le recrutement (de même que
annuel
est le même quel que soit le recrutement (de même que
 et
et ).
).
9. Il faut ajouter que les économistes ont
transformé la capture totale, Y en valeur Y$, le poids moyen
à la capture  , en
prix moyen de poisson,
, en
prix moyen de poisson,  , le
rendement par navire (ou le CPUE) en valeur de la production par navire,
U$, et le niveau de pêche,
, le
rendement par navire (ou le CPUE) en valeur de la production par navire,
U$, et le niveau de pêche,
 en coût
d’exploitation, F$. La différence entre la valeur de la capture
et le coût d’exploitation, Y$-F$, est le profit, L$. La Figure
4.6 illustre un exemple de relation à LT entre ces
caractéristiques utilisées par les économistes contre le
niveau de pêche,
en coût
d’exploitation, F$. La différence entre la valeur de la capture
et le coût d’exploitation, Y$-F$, est le profit, L$. La Figure
4.6 illustre un exemple de relation à LT entre ces
caractéristiques utilisées par les économistes contre le
niveau de pêche,
 .
.
Figure 4.6 Relations à long terme entre la valeur de la capture, le coût d’exploitation et le profit contre le niveau de pêche

La relation stock-recrutement, dénommée relation S-R, met en rapport la taille du stock, pendant 1 an, avec le recrutement résultant de la ponte du stock au cours de cette année. Le recrutement qui s'applique à la relation S-R, est le recrutement à la phase exploitable. Ce recrutement peut avoir lieu la même année que la ponte d’origine ou être déplacé d’une ou de plusieurs années.
Le problème de la relation entre la population parentale et la nouvelle génération n’est pas un cas spécial des ressources halieutiques mais de toutes les populations auto-renouvelables.
Dans chaque cas concret il est important de déterminer quel stock et quel recrutement sont mis en cause. En effet, le stock peut être le nombre total d’individus (au début de l’année ou la valeur moyenne pendant l’année), ou l’effectif des adultes du stock, ou l’effectif des femelles adultes, etc. D’autres caractéristiques peuvent être adoptées, non pas les abondances, en nombre, mais les biomasses respectives. La décision dépendra seulement du type de ressource et des données disponibles. Il faut aussi déterminer le type de recrutement à utiliser. En poids? En nombre? Le recrutement à la zone de pêche? Le recrutement à la phase exploitée?
Sans préoccupation majeure, dans ce manuel, le stock (S) sera la biomasse (totale ou adulte) et le recrutement (R) sera exprimé en nombre.
On note en premier lieu qu’après la ponte, les individus de la nouvelle génération devront passer par différentes phases du cycle biologique: œufs, larves et juvéniles (avant d’être recrues). Ces phases, qui pour quelques espèces peuvent durer quelques années n’intéressent pas directement l’exploitation halieutique. C’est pourquoi la pêche n’affecte pas directement la dimension du nouveau recrutement. C’est vrai que la pêche agit sur la dimension de la biomasse parentale qui à son tour influence le prochain recrutement, mais l’action de la pêche a lieu en dehors de l’intervalle de temps où ont lieu les phases de pré-recrutement antérieurement mentionnées, et c’est précisément pour cet intervalle de temps que l’on estime la relation S-R.
Dans ces phases de pré-recrutement, il existe une grande mortalité due à des facteurs climatiques et environnementaux (vents, courants, températures, etc.) de même que des facteurs biologiques (disponibilité de l’aliment, prédation et autres).
La grande variété de facteurs (non de pêche) et leurs grandes fluctuations rendent complexe la relation S-R, et rendent difficile la création d’un modèle pour expliquer la relation. En conclusion, la relation S-R, entre stock et recrutement qui en résulte, peut être considérée indépendante de la pêche.
Figure 4.7 Exemple de la dispersion des points dans la relation S-R

La Figure 4.7 illustre le type de dispersion des valeurs obtenues quand on marque les recrutements (R) contre les stocks parentaux (S).
En dépit des difficultés, quelques modèles pour la relation S-R ont étés proposés. L’une des raisons en est que l’on croit qu’il doit exister une relation. Un des points de la relation est même connu (S = 0, R = 0).
4.5.1 MODELE DE BEVERTON ET HOLT (1957)
Beverton et Holt, en analysant la pêche de la sole dans les eaux anglaises, ont proposé un modèle que l’on a coutume, actuellement, d’écrire de la façon suivante:
où a et k sont constants
Figure 4.8 Relation S-R de Beverton et Holt

Ce modèle montre une courbe avec R résultante
asymptotique quand S® .
.
4.5.2 MODELE DE RICKER (1954)
Ricker, en étudiant la pêche à la morue de la côte Atlantique canadienne, a proposé un autre modèle qui peut s’écrire sous la forme suivante:
R = a.S.e-S/k
où a et k sont constants.
Figure 4.9 Relation S-R de Ricker

Ce modèle présente un recrutement résultant maximum pour une valeur intermédiaire du stock parental, S.
4.5.3 AUTRES MODELES
D’autres modèles de S-R ont étés proposés, comme le modèle généralisé de Deriso (1980), qui peut être réécrit sous la forme (Hilborn & Walters, 1992):
(quand c = -1 le modèle est celui de Beverton et Holt et quand c®0 le modèle est de Ricker)
ou le modèle généralisé de Shepherd (1982), sous la forme suivante:
(quand c = 1 le modèle est celui de Beverton et Holt et quand c = 2 la courbe est une approximation du modèle de Ricker)
Notez que dans tous les modèles présentés, pour S=0 on aura R=0, comme il était à espérer, et la pente de la tangente à la courbe en ce point, (0,0), est égale au paramètre á. Parfois les relations S-R sont présentées sous la forme R/S en fonction de S.
Ainsi l’équation de Beverton et Holt sera:
montrant que l’inverse de R/S est linéaire avec S.
Avec le modèle de Ricker la relation entre R/S contre S serait:
soit, R/S est exponentiel négatif avec S (ou ln(R/S) est linéaire avec S).
Dans le cas du modèle de Deriso il serait (R/S)c linéaire avec S.
Mathématiquement ces dernières relations peuvent être utiles par leur simplicité, mais statistiquement elles peuvent présenter l’inconvénient que la variable S apparaisse aussi bien comme variable réponse que comme variable auxiliaire (indépendante).
Commentaires
1. Se rappeler que les relations S-R sont indépendantes du niveau de pêche.
2. Les relations S-R peuvent être introduites dans les calculs des prévisions du stock. Dans ce cas, les prévisions à court terme devront être effectuées année par année en exigeant la structure du stock au début de l’année.
3. Il est nécessaire de ne pas oublier qu’il existe une grande dispersion des points (S, R) autour du modèle.
4. Dans le modèle de Deriso quand c = -1 le modèle est celui de Beverton et Holt; quand c ® 0 le modèle tend vers celui de Ricker (pour démontrer la limite de l’équation de Deriso quand c ® 0 il suffit de se rappeler que limite (1+A/n)n = eA quand n ® a).
5. Le modèle de Beverton et Holt
mathématiquement présente une asymptotique, R ® a.k quand S ®  . La valeur de R
donné par ce modèle quand S = k prend la valeur de R = a k/2.
. La valeur de R
donné par ce modèle quand S = k prend la valeur de R = a k/2.
Le modèle de Deriso présente le maximum:
Smax = k / (1+c), Rmax = a.k / (1+c)1+(1/c)
Le modèle de Shepherd présente le maximum:
Smax = k.(c-1)-1/c, Rmax = (a /c).k.(c-1)1-(1/c)
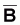 resultante (relation
R-S)
resultante (relation
R-S)Jusqu’à maintenant la discussion a tourné autour de la relation S-R, soit la relation entre la biomasse S et le recrutement R résultant. Il y a une autre relation dont on a parlé à la Section 4.4 (Stock: prévisions à LT, particulièrement dans sa conclusion sur la structure du stock et l’évolution d’une cohorte pendant toute sa vie) que l’on pourrait appeler la relation R-S, c’est-à-dire la relation entre le recrutement R et la biomasse résultante accumulée, Bcum, d’une cohorte pendant toute sa vie exploitée pour un niveau de pêche donné.
La biomasse (ou biomasse de ponte) accumulée d’une cohorte pendant sa vie, Bcum ou BPcum est, comme on l’a déjà vu, égale à:
Bcum= R. {fonction de paramètres biologiques e du régime de pêche, F}
D’autre part, on a déjà noté que la
biomasse accumulée, Bcum, d’une cohorte pendant sa vie
est égale à la biomasse moyenne,
 , du stock pendant un
an, à long terme. Il convient donc de se référer à
Bcum comme
, du stock pendant un
an, à long terme. Il convient donc de se référer à
Bcum comme
 .
.
On peut dire ainsi que si les paramètres biologiques sont considérés constants, alors, pour un régime de pêche donné, la biomasse moyenne pendant un an d’un stock à LT est proportionnelle au recrutement. La Figure 4.10 illustre la proportionnalité.
Figure 4.10 Illustration de la
proportionnalité entre la Biomasse moyenne
( ) d’un stock à
LT et le Recrutement (R), pour un niveau de pêche donné, F, en
supposant constant le régime d’exploitation et les paramètres
biologiques
) d’un stock à
LT et le Recrutement (R), pour un niveau de pêche donné, F, en
supposant constant le régime d’exploitation et les paramètres
biologiques

Noter que dans la Figure 4.5-D, on présente la relation
sous la forme  contre F. Les
deux courbes 4.5-D et la Figure 4.10 sont des représentations
différentes d’une même situation, soit, pour un F
donné, la courbe de la Figure 4.5-D donne la valeur de
contre F. Les
deux courbes 4.5-D et la Figure 4.10 sont des représentations
différentes d’une même situation, soit, pour un F
donné, la courbe de la Figure 4.5-D donne la valeur de
 alors que la droite de la
Figure 4.10 pour une valeur donnée de
alors que la droite de la
Figure 4.10 pour une valeur donnée de
 (pente de la droite) donne
la valeur de F.
(pente de la droite) donne
la valeur de F.
Pour d’autres valeurs de F, la droite aura des inclinaisons différentes. La Figure 4.11 montre diverses droites avec diverses valeurs de F.
Figure 4.11 Illustration de quatre situations à LT pour différents niveaux de pêche, F

La courbe de la Figure 4.9 et la droite de la Figure 4.10 peuvent être superposées dans un même graphique. La Figure 4.12 montre cette superposition, soit la superposition de la courbe S-R de Ricker contre la droite R-S (notez que dans la Figure 4.12 les positions des axes correspondants à la Figure 4.10 ont changé et, donc, quand on mentionne la pente de la droite il importe de noter qu’il s’agit de la pente par rapport à l’axe R).
Figure 4.12 Superposition de la courbe S-R avec la droite R-S pour un F donné

Pour éviter des confusions entre les deux relations on représentera par S-R la relation entre la biomasse et le recrutement résultant et par R-S la relation entre le recrutement et la biomasse moyenne à LT.
Ainsi, on peut illustrer l’analyse conjuguée entre
les deux relations à LT avec un niveau de pêche donné. Pour
une biomasse donnée, la relation S-R détermine le recrutement
futur, recrutement qui à son tour donnera lieu à LT une biomasse
 résultante à
travers la relation R-S, et ainsi successivement jusqu’à une
situation d’équilibre.
résultante à
travers la relation R-S, et ainsi successivement jusqu’à une
situation d’équilibre.
Par exemple, on sélectionne une valeur
 . La courbe S-R permet de
calculer la valeur de R2 résultante. À cette valeur de
R2 correspondra à travers la droite (d’un F donné)
la valeur de B2 résultante à LT, et ainsi
successivement. On peut vérifier dans la Figure 4.13 que le processus
atteint le point d’équilibre (RE,
. La courbe S-R permet de
calculer la valeur de R2 résultante. À cette valeur de
R2 correspondra à travers la droite (d’un F donné)
la valeur de B2 résultante à LT, et ainsi
successivement. On peut vérifier dans la Figure 4.13 que le processus
atteint le point d’équilibre (RE,
 ). Ce point correspondrait
à une valeur du niveau de pêche F. Cette valeur de F peut
être déterminée par la pente de la droite par rapport
à l’axe de R et par la relation à LT de
). Ce point correspondrait
à une valeur du niveau de pêche F. Cette valeur de F peut
être déterminée par la pente de la droite par rapport
à l’axe de R et par la relation à LT de
 contre F.
contre F.
Figure 4.13 Illustration des points successifs qui, en partant d’une biomasse B1, conduisent théoriquement au point d’équilibre (RE, BE)

Notez que l’intersection des deux relations ne conduit pas toujours à un point d’équilibre, ce qui dépend de l’angle à l’intersection entre les deux relations.