Les modèles de production (aussi désignés par modèles de production générale, modèles globaux, modèles synthétiques ou modèles de Lotka-Volterra) considèrent le stock dans sa totalité, soit, ils ne font pas cas de la structure du stock par âges ou longueurs.
La biomasse totale d’un stock non-exploité, ne peut grandir au-delà d’une certaine limite. La valeur de cette limite dépend, pour chaque ressource, de l’espace disponible, de l’accès aux aliments, de la compétition avec d’autres espèces, etc., en résumé, elle dépend des capacités de l’écosystème à maintenir le stock qui y habite. On désignera cette limite par Capacité Soutenable, k.
La biomasse totale d’une ressource halieutique non-exploitée tend à croître vers sa capacité soutenable, k, à un taux, tia(Bt), qui n’est pas constant. Le taux, tia(Bt), est réduit quand la biomasse est petite, croît quand la biomasse croît et est à nouveau réduit quand la biomasse se rapproche de la capacité soutenable. Il convient de noter que la biomasse peut souffrir des altérations, même des diminutions, dues aux fluctuations des facteurs naturels, mais, dans tous les cas, la tendance sera toujours croissante et même sa capacité de soutien.
Ainsi, on peut suggérer que ni tia(Bt) ni tir(Bt) ne sont constants.
En parallèle avec ce qui a été fait avec la supposition de base de la croissance individuelle, on définira une fonction H de Bt, pour l’évolution d’une ressource halieutique non exploitée (“naturelle”), afin de pouvoir adopter la supposition de base suivante:
r est habituellement désigné par taux intrinsèque de croissance de Bt. De cette expression on peut déduire, mathématiquement, tir(Bt), qui est le taux d’intérêt pour le développement des modèles:
Quand le stock est exploité, il convient de séparer tir(Bt) dû à toutes les causes dans deux composants, soit, tir(Bt) dû à la pêche et tir(Bt) dû à toutes les autres causes, désigné par tir(Bt) naturel. Ainsi la supposition de base aura la forme suivante:
On peut dès maintenant, dire que, dans un intervalle de temps Ti où le niveau de pêche est constant, on aura:
Donc, dans l’intervalle Ti, sera:
On a l’habitude de désigner tir(Bt) dû à des causes naturelles seulement par f(Bt) , qui selon la supposition de base de l’évolution naturelle de la biomasse, est supposée être une fonction de la biomasse, Bt.
Commentaires
1. Historiquement les modèles de production ont été les premiers modèles à être utilisés dans l’analyse sur l’évolution de populations biologiques, Lotka-Volterra (1925-1928).
2. Schaefer (1954) a appliqué pour la première fois un modèle de production à un stock halieutique sujet à la pêche.
3. La capacité soutenable, k , est aussi désignée en biologie des pêches par Bsymbol.gif et aussi par Bo. Actuellement on a l’habitude d’utiliser le symbole k (il ne faut pas le confondre avec le symbole, K, des modèles de croissance individuelle ou de la relation S-R).
4. La supposition de base de tir(Bt) du à des causes naturelles, présentée précédemment peut être formulée, mathématiquement, de différentes façons.
5. Les modèles de production, puisqu’ils considèrent la biomasse dans sa totalité et ne font pas cas de la structure par âges ou longueurs, ne peuvent qu’être utilisés dans les pêches pour analyser les effets de changements du niveau de pêche et non pas du régime d’exploitation.
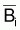 ) dans l’intervalle
T i
) dans l’intervalle
T iLes taux instantanés “total”,
“naturel” et par “pêche” peuvent, dans la pratique,
être rapprochés par des taux moyens relatifs, tmr(Bt).
En effet on peut dire que  par rapport à la moyenne
par rapport à la moyenne
 . (Cette relation est exacte
dans le cas du modèle exponentiel quand tir(B) est pris par rapport
à la moyenne
(
. (Cette relation est exacte
dans le cas du modèle exponentiel quand tir(B) est pris par rapport
à la moyenne
( )).
)).
Ainsi, ayant les taux moyens comme approximation des taux instantanés dans l’expression générale suivante:
on aura:
ou
et
Ainsi, la variation de la biomasse due à toutes les causes de mortalité est décomposée en variation due à la mortalité naturelle et due à la mortalité par pêche:
ou
La situation d’équilibre dans l’intervalle Ti implique que la biomasse du stock à la fin de l’intervalle Ti (généralement 1 an) soit égale à la biomasse au début du même intervalle, c’est-à-dire que la variation finale de la biomasse soit égale à zéro.
Alors, en rapprochant les taux instantanés des taux moyens, quand le stock est en équilibre pendant Ti, on aura DBi=0 et tmr(Bt)=0. Ainsi, une condition d’équilibre sera:
Les conditions d’équilibre sont normalement indiquées avec E en indice. Ainsi:
Dans la pratique, on ne dispose pas toujours de
 et de Fi
d’où la recherche de quantités qui soient associées
à la biomasse, B, et au niveau de pêche, F, mais, plus
concrètement, qui soient des indicateurs de biomasse et du niveau de
pêche. De préférence, il est plus intéressant de
considérer des quantités proportionnelles à ces
paramètres (que l’on désigne par indices).
et de Fi
d’où la recherche de quantités qui soient associées
à la biomasse, B, et au niveau de pêche, F, mais, plus
concrètement, qui soient des indicateurs de biomasse et du niveau de
pêche. De préférence, il est plus intéressant de
considérer des quantités proportionnelles à ces
paramètres (que l’on désigne par indices).
Si l’on désigne par
 l’indice de la biomasse
moyenne,
l’indice de la biomasse
moyenne, 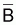 , pendant
l’intervalle de temps, T alors:
, pendant
l’intervalle de temps, T alors:
et si l’on désigne par f l’indice de mortalité par pêche, pendant l’intervalle de temps, T on aura:
de
on
aura
Alors, pour que

Il faudra que
Un indice de
 , assez commun, est la
capture par unité d’effort (cpue). Pour indice de F on utilise
l’effort de pêche en unités appropriées de façon
à être proportionnel au niveau de pêche.
, assez commun, est la
capture par unité d’effort (cpue). Pour indice de F on utilise
l’effort de pêche en unités appropriées de façon
à être proportionnel au niveau de pêche.
La constante de proportionnalité, q, est désignée par coefficient de capturabilité et indique la fraction de la biomasse qui est capturée par unité d’effort.
Pour ces modèles on peut aussi définir des points de référence biologique.
On a l’habitude de désigner par FMSY la valeur de F qui rend la capture maximum, Y.
FMSY est différent de Fmax. En effet, FMSY maximise la Capture en poids, alors que Fmax, maximise la Capture en poids par Recrue. A noter que dans un modèle de production on ne peut calculer Fmax, puisqu’on le considère inconnu - implicite dans les suppositions de bases du modèle - la structure par longueurs du stock (et donc le recrutement, R).
A noter que le FMSY des modèles structuraux est différent du FMSY des modèles de production. Il suffit de considérer la relation S-R ainsi que le coefficient de mortalité naturel, M, qui sont implicites dans les modèles de production, ne pouvant pas être explicités.
La comparaison ou mélange de résultats des deux types de modèles devra faire cas des différentes suppositions de base sur lesquelles chaque modèle se base.
Pour les mêmes raisons, F0.1 des modèles de production est un concept différent du F0.1 des modèles structuraux.
Pour le calcul de F0.1, B0.1 et Y0.1 on peut procéder de la même façon que dans le cas des modèles structuraux, mais avec les modèles de production il est préférable de recourir aux relations, constantes, entre les points de référence 0.1 et MSY (Cadima, 1991).
Les modèles de production les plus utilisés dans les évaluations des ressources halieutiques sont le modèle de Schaefer (1954), le modèle de Fox (1970) et le modèle de Pella et Tomlinson (1969), qui est aussi désigné par GENPROD (nom du logiciel que les auteurs ont élaboré pour l’application de leur modèle). Fox mentionne que l’élaboration de son modèle est basé sur une idée de Garrod (1969).
À chacun de ces modèles correspondra une fonction particulière de H(Bt) dans la supposition de base.
6.7.1 MODÈLE DE SCHAEFER
Pour ce modèle de production la fonction H(Bt) de la supposition de base sera:
Taux instantané relatif, tir(Bt), dû à des causes naturelles
De l’expression de la supposition de base générale, on aura:
et le taux instantané de variation de la biomasse “naturelle” peut être déduit mathématiquement de cette expression et écrit ainsi:
Conditions d’équilibre
En rapprochant tir(Bt) de
tmr(Bt), relatif à
 , on aura:
, on aura:
et, comme en équilibre
 , les conditions
d’équilibre peuvent être exprimées ainsi:
, les conditions
d’équilibre peuvent être exprimées ainsi:
Notez
que est linéaire avec
FE et pour FE = 0 on aura
est linéaire avec
FE et pour FE = 0 on aura
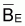 = k = biomasse
vierge.
= k = biomasse
vierge.
Graphiquement, la relation
entre et FE montre
une droite où l’ordonné à l’origine est
égal à k et la pente est égale à -k/r.
et FE montre
une droite où l’ordonné à l’origine est
égal à k et la pente est égale à -k/r.
Point-cible, FMSY
Pendant 1 an, les conditions d’équilibre pourront être écrites ainsi:
|
|
|
et Y maximum aura lieu quand dY/dF=0. En dérivant l’expression précédente de YE par rapport à F et égale à zéro, on aura:
Point-cible, FMSY (Schaefer)
|
FMSY = r/2 |
BMSY = k/2 |
YMSY = rk/4 |
En effet la dérivée
ou
dY/dF = k(1- F/r) + F (- k/r) = k - 2k.F/r
et, donc,
FMSY = r/2
les autres relations sont obtenues en substituant ce résultat dans les conditions d’équilibre.
Point-cible, F0.1
On prouve que le quotient entre F0.1 et FMSY est constant et égal à 0.90. Ainsi, on peut conclure que:
Point-cible, F0.1 (Schaefer)
|
F0.1/ FMSY = 0.90 |
B0.1 /BMSY = 1.10 |
Y0.1 /YMSY = 0.99 |
En effet, comme on l’a déjà vu auparavant, dY/dF = k - 2k.F/r et, comme F0.1 correspond à dY/dF = 0.1k , on aura:
0.1k = k - 2kF0.1/r
ou
0.90 = 2 F0.1/r
ou
0.90 =F0.1/FMSY
Indices d’abondance,
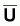 , et indices du niveau de
pêche, f
, et indices du niveau de
pêche, f
Comme on l’a vu dans la Section 6.5, on suppose que les
indices et f sont
proportionnels à
et f sont
proportionnels à  et
F. Pour ce modèle la condition d’équilibre pourra être
écrite ainsi:
et
F. Pour ce modèle la condition d’équilibre pourra être
écrite ainsi:
|
|
et |
|
(a,b sont constants). |
Le point-cible, fMSY, peut être obtenu avec la dérivée de YE à l’ordre de fE égale à zéro:
Point-cible, fMSY (Schaefer)
|
fMSY = -a/(2b) |
|
YMSY = - a2/(4b) |
On prouve que, dans les modèles de production, les
quotients f0.1/fMSY et
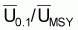 sont égaux aux
quotients F0.1/FMSY et
sont égaux aux
quotients F0.1/FMSY et
 . Dans le cas du
modèle de Schaefer il sera donc:
. Dans le cas du
modèle de Schaefer il sera donc:
Point-cible, f0.1 (Schaefer)
|
f0.1/ fMSY = 0.90 |
|
Y0.1/YMSY = 0.99 |
De 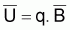 ,
FT=q.f et des expressions précédentes des points-cible relatifs
à FMSY et fMSY on peut aussi obtenir les relations
des paramètres k et r avec les coefficients a, b et q:
,
FT=q.f et des expressions précédentes des points-cible relatifs
à FMSY et fMSY on peut aussi obtenir les relations
des paramètres k et r avec les coefficients a, b et q:
|
k = a/q |
r = - aq/(bT) |
kr = - a2/(bT) |
Quand la valeur de l’intervalle T est d’un an, T n’apparaît pas dans les expressions. Ces expressions permettent le calcul des paramètres du modèle, k et r, dès que l’on connaît la valeur du coefficient de capturabilité, q. Notez que le produit k.r ne dépend pas de q.
6.7.2 MODELE DE FOX
Pour le modèle de production de Fox la fonction H(Bt) sera:
H(Bt) = ln(Bt)
Taux instantané relatif, tir(Bt), du à des causes naturelles
De l’expression de la supposition de base générale on aura pour le modèle de Fox:
tirnaturel [ lnk -lnB ] = - r
et donc, comme mentionné plus haut, le taux instantané de variation de la biomasse “naturelle” peut être déduit mathématiquement de cette expression, et dans ce cas, écrite ainsi:
Conditions d’équilibre
La condition d’équilibre de la biomasse peut être exprimée ainsi:
et, donc, les conditions d’équilibre seront:

Notez que  est linéaire avec FE et que pour FE = 0 on aura
est linéaire avec FE et que pour FE = 0 on aura
 .
.
La relation entre
 et FE est
linéaire, avec l’ordonné à l’origine = lnk et
déclive = -1/r.
et FE est
linéaire, avec l’ordonné à l’origine = lnk et
déclive = -1/r.
Point-cible, FMSY
En dérivant YE de F et avec la dérivée égale à zéro, on aura:
|
FMSY = r |
BMSY = k/e |
YMSY = rk/e |
Point-cible, F0.1
Dans ce modèle le quotient entre F0.1 et FMSY est constant et égal à 0.7815. On peut ainsi conclure que:
|
F0.1/ FMSY = 0.7815 |
B0.1 /BMSY = 1.2442 |
Y0.1 /YMSY = 0.9724 |
Ces résultats sont obtenus de la même façon que dans le cas du modèle de Schaefer. L’équation à résoudre sera:
ce qui exige des méthodes itératives pour trouver F0.1/r. La solution sera F0.1/r = 0.7815 ou égal à F0.1/FMSY.
Indices d’abondance,
 , et indices du niveau
de pêche, f
, et indices du niveau
de pêche, f
Pour le modèle de Fox la condition d’équilibre pourra être écrite ainsi:
et
Le point-cible, fMSY , peut être obtenu avec la dérivé de YE à l’ordre de fE égale à zéro:
Point-cible, fMSY
|
fMSY = -1/b |
|
YMSY = - ea/be |
Les quotients f0.1/fMSY et
 sont, dans le cas du
modèle de Fox, égaux à F0.1/FMSY et
sont, dans le cas du
modèle de Fox, égaux à F0.1/FMSY et
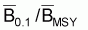 et donc:
et donc:
Point-cible, f0.1
|
f0.1/ fMSY = 0.7815 |
|
Y0.1 /YMSY = 0.9724 |
De 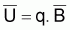 et de
FT=q.f on peut conclure que:
et de
FT=q.f on peut conclure que:
|
k = ea/q |
r = - q/(bT) |
kr = - ea/(bT) |
Quand la valeur de l’intervalle T est d’un an, T n’apparaît pas dans ces expressions. La dernière expression permet le calcul du produit k.r. Pour calculer k et r séparément il faut connaître la valeur du coefficient de capturabilité, q, et utiliser les deux autres expressions.
6.7.3 MODÈLE DE PELLA ET TOMLINSON (GENPROD)
Pour ce modèle de production la fonction H(Bt) sera:
Taux instantané relatif, tir(Bt), du à des causes naturelles
De l’expression de la supposition de base générale on aura pour le modèle GENPROD:
d’où
Conditions d’équilibre
En équilibre on aura
Et, donc, les conditions d’équilibre peuvent être exprimées ainsi:
|
|
|
Notez que la relation entre
( )p et
FE est linéaire avec l’ordonné à
l’origine égal à k et la pente égale à -pk/r.
Donc pour FE = 0 on aura
)p et
FE est linéaire avec l’ordonné à
l’origine égal à k et la pente égale à -pk/r.
Donc pour FE = 0 on aura
 = k = biomasse
vierge
= k = biomasse
vierge
Point-cible, FMSY
En dérivant YE à l’ordre de F et avec la dérivée égale à zéro, on aura:
Point-cible, FMSY (Pella et Tomlinson)
|
|
|
|
Point-cible, F0.1
Le quotient entre F0.1 et FMSY est constant pour chaque valeur de p et peut être obtenu comme dans les cas précédents. L’équation à résoudre par itérations serait:
X= 1 - 0.1.[1-p/ (1+p).X]1/p
où
X=F0.1/ FMSY
et aussi
B0.1/ BMSY = [1+p - p./ (1+p).X](1+1/p)
Y0.1/ YMSY = [F0.1/ FMSY].[ B0.1/ BMSY]
Le tableau suivant résume les résultats les plus importants:
| |
paramètre p |
F0.1/FMSY |
B0.1/BMSY |
Y0.1/YMSY |
| Fox |
0.0 * |
0.781521 |
1.244182 |
0.972355 |
| 0.2 |
0.819995 |
1.193441 |
0.978616 |
|
| 0.4 |
0.848355 |
1.158613 |
0.982915 |
|
| 0.6 |
0.869888 |
1.133469 |
0.985991 |
|
| 0.8 |
0.886657 |
1.114599 |
0.988268 |
|
| Schaefer |
1.0 * |
0.900000 |
1.100000 |
0.990000 |
| 1.2 |
0.910816 |
1.088420 |
0.991350 |
|
| 1.4 |
0.919724 |
1.079045 |
0.992424 |
|
| 1.6 |
0.927165 |
1.071323 |
0.993293 |
|
| 1.8 |
0.933457 |
1.064867 |
0.994008 |
|
| 2.0 |
0.938835 |
1.059401 |
0.994602 |
|
| 2.2 |
0.94377 |
1.054720 |
0.995704 |
|
| 2.4 |
0.947516 |
1.050674 |
0.995531 |
|
| 2.6 |
0.951059 |
1.047146 |
0.995898 |
|
| 2.8 |
0.954188 |
1.044045 |
0.996216 |
|
| 3.0 |
0.956969 |
1.041302 |
0.996494 |
Notez que (F0.1/FMSY) + (B0.1/BMSY) @ 2. A partir de ce résultat on peut affirmer que quand F0.1 est inférieur à FMSY d’un certain pourcentage, la relation équivalente des biomasses sera plus grande et à peu près au même pourcentage.
Indices d’abondance,
 , et indices
du niveau de pêche, f
, et indices
du niveau de pêche, f
Pour le modèle de Pella et Tomlinson la condition d’équilibre pourra être écrite ainsi:
= (a + b.f)1/p
ou
= (a + b.f) (a,b sont des constantes).
Le point-cible, fMSY , peut être obtenu avec la dérivé de YE à l’ordre de fE égale à zéro.
Point-cible, fMSY
|
fMSY = -a/(b(1+1/p)) |
|
YMSY = -(p/b).(a/(1+p))(1+1/p) |
Les quotients f0.1/fMSY et
 seront égaux aux
quotients F0.1/FMSY et
seront égaux aux
quotients F0.1/FMSY et
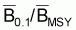 , respectivement. Ces
derniers quotients peuvent être observés dans la table
précédente.
, respectivement. Ces
derniers quotients peuvent être observés dans la table
précédente.
On peut aussi obtenir les valeurs de k, r et k.r
à partir de  , et
de F.T=q.f
, et
de F.T=q.f
|
k = (1/q) a1/p |
r = - aqp/(bT) |
k.r = (-p/bT)a(1+1/p) |
Quand la taille de l’intervalle est d’un an, T n’apparaît pas dans ces expressions. La dernière expression de la table précédente permet le calcul du produit k.r. Les valeurs séparées de k et r peuvent être calculée dès que l’on connaît la valeur du coefficient de capturabilité, q.
Commentaires
1. Le modèle de Pella et Tomlinson a été et est critiqué dans son application pratique car il produit, parfois, de meilleurs ajustements à des valeurs non crédibles du paramètre p, résultant en des valeurs extrêmement élevées de FMSY.
2. Il convient faire aussi attention à ce que p, paramètre additionnel de ce modèle, est référé par différents symboles selon les auteurs.
3. Les valeurs des points de référence biologiques relatives à F, estimées par le modèle de Schaefer, sont plus restrictives que les valeurs correspondantes estimées par d’autres modèles de production
6.8.1 Méthodes générales
Les modèles de production ont été utilisés dans les pêches pour les prévisions à LT. C’est à partir des années 90 que des méthodes d’application des modèles de production aux prévisions à court terme, CT, ont été développées. Ces méthodes ont pour base les expressions de Schaefer, de Fox et de Pella et Tomlinson pour l’évolution de la biomasse non exploitée.
Comme il l’a été dit dans la Section 6.3, la variation de la biomasse pendant 1 an peut être exprimée, d’une façon générale, comme:
ou
où
Bi = biomasse au début de l’année i
Bi+1= biomasse à la fin de l’année i
=bomasse moyenne pendant l’année i
Yi = capture en poids pendant l’année i
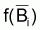 est
l’approximation du taux moyen de variation "naturelle" de la biomasse, par
rapport à
est
l’approximation du taux moyen de variation "naturelle" de la biomasse, par
rapport à 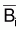 , pendant
l’année i.
, pendant
l’année i.
L’expression de la variation de la biomasse sert de base à la majeure partie des méthodes de prévision à CT. Des programmes informatiques on étés préparés pour l’application de ces méthodes, qui déterminent aussi des prévisions à LT, des points de référence biologique, etc. En sont exemples CEDA et BYODIN, de la responsabilité de Rosenberg et al. (1990), et de Punt et Hilborn (1996) respectivement.
Théoriquement ces méthodes supposent que
 et Yi sont
connus pendant une certaine période d’années. La fonction
et Yi sont
connus pendant une certaine période d’années. La fonction
 peut être celle de
Schaefer, de Fox, ou de Pella et Tomlinson.
peut être celle de
Schaefer, de Fox, ou de Pella et Tomlinson.
Pour déterminer les paramètres r et k il
faudrait adopter une des expressions
 et la valeur B1
du premier intervalle de la période de temps.
et la valeur B1
du premier intervalle de la période de temps.
Dans la pratique on ne dispose pas de biomasses moyennes
annuelles, mais seulement de quantités associées, normalement
supposées proportionnelles aux biomasses moyennes, soit aux indices
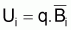 . Ainsi il y aura 3
paramètres à estimer, r, k et q (voir Chapitre7).
. Ainsi il y aura 3
paramètres à estimer, r, k et q (voir Chapitre7).
La fonction objet à minimiser peut être F = S(Uobs -
Umod) 2 , soit, la somme des carrés des erreurs
entre les valeurs observées et estimées (désignée
par erreur du procès). Cependant, quand on utilise les valeurs de U
observées et on suppose que la relation
 n’est pas
déterministe, mais contient une erreur, désignée par
erreur d’observation, donnée par F
estimé, on préfère alors adopter la fonction objet F = S (lnUobs -
lnUmod)2 (Punt et Hilborn, 1996).
n’est pas
déterministe, mais contient une erreur, désignée par
erreur d’observation, donnée par F
estimé, on préfère alors adopter la fonction objet F = S (lnUobs -
lnUmod)2 (Punt et Hilborn, 1996).
6.8.2 METHODE DE PRAGER (1994)
Prager (1994) n’a pas utilisé l’expression de base initiale comme étant le taux moyen mais le taux instantané relatif de la variation de la biomasse dans l’année i et a adopté le modèle de Schaefer, soit,
tir(Bt) = r[1 - Bt / k]. Bt - Fi. Bi
Intégrant cette expression pendant l’année i il a obtenu la relation entre Bi+1 et Bi
D’un autre côté en calculant la biomasse
moyenne,  , pendant
l’année i en intégrant Bt entre ti et
ti+1. Finalement il a calculé la capture en poids comme
étant:
, pendant
l’année i en intégrant Bt entre ti et
ti+1. Finalement il a calculé la capture en poids comme
étant:
.
L’estimation des paramètres peut alors être réalisée de la même manière que les méthodes précédentes. Le logiciel préparé à cet effet est dénommé ASPIC (Prager, 1995).
6.8.3 METHODE DE YOSHIMOTO ET CLARKE (1993)
Les prévisions à CT sont dérivées de la supposition de base des modèles de production définie comme:
ou, représentant
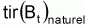 par
f(Bt):
par
f(Bt):
Ainsi, en intégrant cette expression pour l’intervalle de temps Ti en considérant que
tir(Bt) = tia ln(Bt)
et que Ft = Fi =constant:
Pour l’intervalle Ti+1 suivant (qui est l’intervalle des prévisions pour le stock et la capture) on aurait:
Pour calculer la moyenne arithmétique simple des expressions précédentes pour les intervalles Ti et Ti+1, on aura dans le premier terme:
1/2[ln (Bi+1) + ln (Bi+2)] - 1/2[ln (Bi) + ln (Bi+1)] =
où  est la moyenne géométrique de Bi et Bi+1, et
est la moyenne géométrique de Bi et Bi+1, et
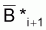 est la moyenne
géométrique de Bi+1 et Bi+2.
est la moyenne
géométrique de Bi+1 et Bi+2.
Ainsi, la moyenne des deux expressions sera:
Dans le cas du modèle de Fox, on a f(Bt) = r
(lnk - lnBt) et, donc,
 peut
s’écrire:
peut
s’écrire:
où 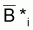 est la moyenne géométrique de Bi et
Bi+1.
est la moyenne géométrique de Bi et
Bi+1.
Dans ce cas, l’expression précédente, relative aux moyennes géométriques, peut se réécrire ainsi:
Pour simplifier et, parce que normalement les intervalles de Ti sont constants et égaux à un an, on utilisera au lieu de Ti et Ti+1 simplement T et l’expression sera:
ou en réorganisant les termes de l’expression, on aura:
Finalement, l’expression peut s’écrire de la façon suivante:
= 2rT/(2+rT). lnk + (2- rT)/(2+rT).
- T/(2+rT). (Fi + Fi+1)
Comme on l’a vu dans les prévisions à LT
(ou en équilibre) il est plus commun d’avoir des indices de
biomasse, 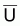 , et de niveau de
pêche f, que des valeurs de
, et de niveau de
pêche f, que des valeurs de
 et F.
et F.
En utilisant les indices
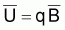 et qf = FT
et qf = FT
on peut écrire l’expression de Yoshimoto et Clarke (1993):
Dans la pratique, il est plus utile d’écrire cette expression comme suit:
ln
= b1 + b2. ln
+ b3. (fi + fi+1)
où:
À partir des coefficients b1, b2 et b3 on peut estimer les paramètres q, r et k (se rappeler que dans les prévisions à LT il n’était pas possible d’obtenir q isolément). Ainsi:
q = -4b3/(1+b2)
rT = 2(1-b2) / (1+b2)
k = ((1+b2)/(-4b3)).eb1/(1-b2)
Commentaires
1. A noter que le fait d’avoir développé dans ce manuel le modèle de Yoshimoto et Clarke pour les prévisions à CT ne signifie pas une préférence spéciale par rapport à d’autres modèles pour les prévisions à CT.
2. Yoshimoto et Clarke ont désigné leur expression comme expression intégrée de Fox, en raison du fait d’avoir pour base l’intégration directe de la supposition de base.
3. Notez que
 et
et
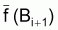 sont, en
général, différents de
sont, en
général, différents de
 et
et
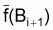 . Cependant, les moyennes de
f() peuvent être considérées égales à
f(moyennes de B) si l’on utilise un autre type de moyenne de B.
. Cependant, les moyennes de
f() peuvent être considérées égales à
f(moyennes de B) si l’on utilise un autre type de moyenne de B.
Définition
de 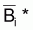 selon une fonction
selon une fonction
On considére n valeurs Bi et la moyenne arithmétique simple de f(Bi), soit
f(B) =(1/n). S f(Bi)
Soit
 une
valeur telle que
une
valeur telle que
 .
.
 est
désignée comme la moyenne de Bi selon la fonction
f.
est
désignée comme la moyenne de Bi selon la fonction
f.
EXEMPLES
4. Si f(B) = ln(B) alors
 = (1/n). Sln(Bi) et ainsi
= (1/n). Sln(Bi) et ainsi
 est la moyenne des valeurs
Bi selon la fonction logarithme népérien, aussi
désignée par moyenne géométrique des valeurs
Bi
est la moyenne des valeurs
Bi selon la fonction logarithme népérien, aussi
désignée par moyenne géométrique des valeurs
Bi
5. Au cas où f(B) = B-1 alors
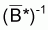 = (1/n). ). S(Bi)-1 et
= (1/n). ). S(Bi)-1 et
 est désignée
par moyenne harmonique des valeurs Bi
est désignée
par moyenne harmonique des valeurs Bi
6. Si f(B) = B-p on aura alors
 =(1/n). ). S(Bi)-p et
=(1/n). ). S(Bi)-p et
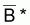 est désignée
par moyenne d’ordre (-p) des valeurs Bi.
est désignée
par moyenne d’ordre (-p) des valeurs Bi.
7. Une autre approximation (Cadima & Pinho, 1995) de l’équation intégrée de Fox peut être:
= b1 + b2.
+ b3. (fi + fi+1)
où:
|
b1= (1-e-rT) ln(qk) |
|
b2= e-rT
soit
rT = -lnb2
|
b3= - q(1-e-rT) / (2rT) |
|
Cette approximation de l'équation intégrée du modèle de Fox peut être développée à partir de la supposition de base du modèle de Fox, dans l’intervalle Ti, et donne l’expression suivante:
Ainsi, en accord avec les propriétés des taux, et en attendant que r, k et Fi soient constants dans l'intervalle Ti, on peut écrire le taux instantané absolu de [r.(lnK-lnBt)-Fi] ainsi:
tia[r.(lnK-lnBt)-FI]=-r.tia(lnBt)=-r.tir(Bt)
En remplaçant tir(Bt) par l'expression de Fox indiquée, on aura:
tia[r.(lnK-lnBt)-Fi]=-r. [r.(lnK-lnBt)-Fi]
ou, en divisant les deux membres par l'expression entre crochets, on aura:
Donc, par définition de tir, [r.(ln k - ln Bt)-Fi] suit un modèle exponentiel pendant l'intervalle Ti avec la constante -r.
Alors, la valeur finale de (r.ln k - r.ln Bt - Fi) peut s’exprimer ainsi:
(r.ln k - r.ln Bi+1 - Fi) = (r.ln k - r.ln Bi - Fi). e-r.Ti
ou
ln Bi+1 = (1- e-r.Ti).ln k + e-r.Ti.ln Bi - (1- e-r.Ti).Fi/r
Dans l’intervalle suivant, Ti+1, serait:
ln Bi+2 = (1- e-r.Ti+1).ln k + e-r.Ti+1.ln Bi+1 - (1- e-r.Ti+1).Fi+1/r
donc, la moyenne des deux expressions précédentes, en considérant Ti=Ti+1=T sera:
ln
= (1- e-r.T).ln k + e-r.T. ln
- ((1- e-r.T) / 2r).(Fi+Fi+1)
où
 = moyenne
géométrique de Bi et Bi+1 et
= moyenne
géométrique de Bi et Bi+1 et
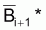 = moyenne
géométrique de Bi+1 et Bi+2.
= moyenne
géométrique de Bi+1 et Bi+2.
En utilisant les indices
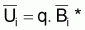 et qfi =
FiT on aura:
et qfi =
FiT on aura:
ln
= (1- e-r.T).ln (qk) + e-r.T.
- ((1- e-r.T)/2rT).q(fi+fi+1)
qui est équivalent à l’expression précédente de ce dernier commentaire.