Dans les chapitres antérieurs plusieurs modèles utilisés dans l’évaluation des stocks ont été analysés, et leurs paramètres ont étés définis. Dans les fiches d’exercices correspondantes les valeurs des paramètres ont été données, leur estimation n’étant pas nécessaire. Dans ce chapitre on analysera plusieurs méthodes d’estimation des paramètres. Il faut se rappeler que l’estimation de paramètres implique des connaissances de la théorie de l’échantillonnage et d’inférence statistique.
Dans ce manuel on se référera à l’une des méthodes générales les plus utilisées en estimation de paramètres - la méthode des moindres carrés. Cette méthode utilise, dans plusieurs cas, des procédés itératifs d’estimation qui requièrent des valeurs initiales proches des vraies valeurs des paramètres. Ainsi, on présente aussi quelques méthodes particulières, qui permettent d’obtenir facilement des estimations proches des vraies valeurs des paramètres. De toute façon, ces estimations rapprochées ont aussi, par elles-même, un intérêt pratique. Ces méthodes seront illustrées avec l’estimation des paramètres de croissance et de la relation S-R, stock-recrutement.
La méthode des moindres carrés est présentée sous la forme de régression linéaire simple, de modèle linéaire multiple et de modèles non linéaires (méthode de Gauss-Newton).
Des sujets comme l’analyse de résidus, distribution dans l’échantillonnage des estimateurs (asymptotiques ou empiriques "Bootstrap" et "jacknife"), limites et intervalles de confiance, etc., sont importants dans l'estimation de paramètres. Cependant, pour aborder ces sujets il faudrait un cours de durée supérieure.
Modèle
Considérez les variables et paramètres suivants:
|
Variable réponse (ou dépendante) |
= Y |
|
Variable auxiliaire (ou indépendante) |
= X |
|
Paramètres |
= A, B |
La variable réponse est linéaire avec les paramètres
Y = A+BX
Objectif
Observées n paires de valeurs (chaque paire est constituée par une valeur sélectionnée de la variable auxiliaire et la valeur observée correspondante de la variable réponse), évaluer les paramètres du modèle, soit:
Observés xi et yi pour chaque paire i, avec i=1,2,...,i,...n
Évaluer A et B et (Y1,Y2,...,Yi,...,Yn) pour les n paires de valeurs observées
(Valeurs estimées
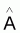 et
et
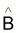 (ou a et b) et
(ou a et b) et
 )
)
Fonction objet (ou fonction critère)
Critère d'estimation
Les estimateurs seront les valeurs de A et B qui minimisent la fonction objet. Ce critère est dénommé méthode des moindres carrés. Pour procéder à la minimisation il faut que les dérivés ¶F/¶A et ¶F/¶B égalent zéro et résoudre le système d'équations obtenu à l'ordre de A et de B.
La résolution du système d'équations, après quelques transformations mathématiques, donne les résultats suivants:
|
|
|
|
|
|
|
b = Sxy/Sxx |
|
Notez que les valeurs yi observées, pour un même ensemble de valeurs de X sélectionnées dépendent de l'échantillon recueilli. Statistiquement le problème de la régression linéaire simple est présenté en écrivant le modèle comme suit:
y = A + BX + e
où e est une variable aléatoire avec une valeur espérée égale à zéro et variance égale à s2.
Ainsi, la valeur espérée de y sera Y ou A+BX et la variance de y sera égale à la variance de e.
On a l’habitude de différencier l'écart et le résidu:
L'écart est la différence entre
yobservé et ymoyen
 , soit écart =
, soit écart =

alors que
Résidu est la différence entre
yobservé et Yestimé
(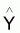 ), soit résidu =
(yi -
), soit résidu =
(yi - ).
).
Il convient, pour l'analyse de l'ajustement du modèle aux données observées, de considérer les caractéristiques suivantes:
Somme des carrés des résidus égale à:
Cette quantité indique la variation résiduelle des valeurs observées par rapport aux valeurs estimées du modèle, soit, la variation des valeurs observées qui n'est pas expliquée par le modèle.
Somme des carrés des écarts des valeurs estimées du modèle égale à:
Cette quantité indique la variation des valeurs estimées de la variable réponse du modèle par rapport à sa moyenne, soit, la variation des valeurs estimées de la variable réponse expliquée par le modèle.
Somme totale des carrés des écarts des valeurs observées égale à:
Cette quantité indique la variation totale des valeurs observées par rapport à la moyenne.
La relation suivante est facile à vérifier:
SQtotal = SQmodèle + Sqrésiduel
ou

ou
1 = r2 + (1 - r2)
où:
r2 (coefficient de détermination) est le pourcentage de variation totale qui est expliquée par le modèle et,
1-r2 est le pourcentage de variation totale qui n’est pas expliquée par le modèle.
Modèle
Considérez les variables et paramètres suivants:
|
Variable réponse (ou dépendante) |
= Y |
|
Variables auxiliaires (ou indépendantes) |
= X1, X2,..., Xj,..., Xk |
|
Paramètres |
= B1, B2,..., Bj,..., Bk |
La variable réponse est linéaire avec les paramètres:
Y = B1X1+B2X2+... + BkXk =S BjXj
Objectif
Observés n ensembles de valeurs (chaque ensemble est formé par une valeur observée de chaque variable auxiliaire et la valeur observée correspondante de la variable réponse) évaluer les paramètres du modèle, soit:
|
observés |
x1,i x2,i ,..., xj,i,.., xk,i et yi pour chaque ensemble i, avec i=1,2,...,i,...n |
|
évaluer |
B1,B2,...,Bj,...,Bk et (Y1,Y2,...,Yi ,...,Yn) pour les n ensembles observés |
Les valeurs estimées peuvent être représentées par:
,
,...,
,...,
(ou b1,b2,...,bj,...,bk) et
,
,...,
,...,
Fonction objet ou fonction critère
Critère d’estimation
Les estimateurs seront des valeurs de Bj qui minimisent la fonction objet. Ce critère est appelé méthode des moindres carrés.
D’une manière semblable à celle utilisée dans le cas du modèle linéaire simple, la procédure de minimisation nécessite d’égaler à zéro les dérivées partielles de F à l’ordre de chaque paramètre, Bj avec j=1, 2,..., k. Cette procédure est, préférablement, traitée avec le calcul matriciel.
Version matricielle
Matrice
Matrice des valeurs observées des variables auxiliaires
Vecteur
Vecteur des valeurs observées de la variable réponse
Vecteur
Vecteur des valeurs de la variable réponse (non observées)
Vecteur
Vecteur des Paramètres
Vecteur
ou
Vecteur des estimateurs des paramètres
Modèle
Y(n,1) = X(n,k). B(k,1) ou Y=X.B+e
Fonction objet
|
F (1,1) = (y-Y)T.(y-Y) ou |
F(1,1) = (y-X.B)T.(y-X.B) |
Pour calculer les estimateurs des moindres carrés il faut que la dérivée de F à l’ordre du vecteur B soit égale à zéro. On rappele que dF/dB est un vecteur avec composants dF/dB1, dF/dB2,..., dF/dBk. Ainsi, on aura:
dF/dB(k,1) = -2.XT.(y-X.B) = 0
ou
XTy - (XT.X). B = 0
et
b =
= (XT.X)-1. XTy
Les résultats peuvent s’écrire ainsi:
b(k,1) = (XT.X)-1.XTy
ou
résidus(n,1) = (y-
)
Commentaires
Pour l’analyse statistique il est avantageux d’exprimer les estimateurs et les sommes des carrés en utilisant des matrices idempotentes. Ensuite on utilise les matrices idempotentes L, (I - L) et (I - M) avec L(n,n) = X (XT. X)-1. XT, I = matrice unitaire et M(n,n) = matrice moyenne(n,1) = 1/n [1] où [1] est une matrice où tous les éléments sont égaux à l’unité.
Il faut aussi considérer les distributions des estimateurs dans l’échantillonnage et supposer que les valeurs ei sont indépendantes et ont une distribution normale.
Il convient de noter dès maintenant quelques propriétés de l'espérance et de la variance d’une relation linéaire d’une variable aléatoire u. En termes matriciels on considère c1 un vecteur constant de dimension (n.1), c2 une matrice de valeurs constantes et dimension (n.n) et le vecteur aléatoire u de dimension (n.1). Ainsi:
|
|
E[c1+c2.u] = c1+c2.E[u] |
V[c1+c2.u] = c2.V[u].c2T |
|
1 - |
Variable aléatoire, e |
en. (indépendantes) |
|
|
Espérance de e |
E[e] = 0 |
|
|
Variance de e égale à |
V[e](n.n) = E[e.eT]=I. s2 |
|
2 - |
Variable réponse y observée |
y = Y+e |
|
|
Espérance de y |
E[y] = Y = X.B. |
|
|
Variance de y égale à |
V[y](n.n) = V[e](n.n) = I. s2 |
|
3 - |
Estimateur du vecteur paramètre B |
|
|
|
Espérance de
|
E[ |
|
|
Variance de
|
V[ |
|
4 - |
Estimateur de Y du modèle |
|
|
|
Espérance de
|
E[ |
|
|
Variance de
|
[ |
|
5 - |
Résidu e |
e = y- |
|
|
Espérance de e |
E[e] = 0 |
|
|
Variance de e |
V[e] = (I-L).. s 2 |
|
6 - |
Somme des carrés |
|
6.1 - Somme résiduelle des carrés = SQ
résiduel(1.1) =
(y-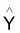 )T(y-
)T(y- )
= yT (I-L)y
)
= yT (I-L)y
Cette quantité indique la variation résiduelle des valeurs observées par rapport aux valeurs du modèle, soit, la variation qui n’est pas expliquée par le modèle.
6.2 - Somme des carrés du modèle = SQ
modèle(1.1) =
( -
- )T(
)T( -
- )
= yT (L-M)y
)
= yT (L-M)y
Cette quantité indique la variation des valeurs du modèle par rapport à la moyenne, soit, la variation expliquée par le modèle.
6.3 - Somme totale des carrés des écarts
= SQ total(1.1) =

Cette quantité indique la variation totale des valeurs observées par rapport à la moyenne.
La relation suivante est facile à vérifier:
SQtotal = SQmodèle + SQrésiduel
ou
ou
1 = R2 + (1 - R2)
où:
R2 est le pourcentage de variation totale qui est expliquée par le modèle.
En termes matriciels:
R2 = [yT(L - M)y].[ (yT(I - M)y]-1
1-R2 est le pourcentage de variation totale qui n’est pas expliquée par le modèle.
Les valeurs caractéristiques des matrices (I-L), (I-M) et (L-M) respectivement égales à (n-k), (n-1) et (k-1), sont les degrés de liberté associés aux sommes des carrés respectives.
Modèle
Considérez les variables et paramètres suivants:
|
Variable réponse (ou dépendante) |
= Y |
|
Variable auxiliaire (ou indépendante) |
= X |
|
Paramètres |
= B1,B2,...,Bj,...,Bk |
La variable réponse est non-linéaire avec les variables auxiliaires
Y = f(X;B) où B est un vecteur de composants B1,B2,...,Bj,...,Bk
Objectif
Observées n paires de valeurs (chaque paire est constituée d’une valeur sélectionnée de la variable auxiliaire et d’une valeur observée correspondante de la variable réponse) évaluer les paramètres du modèle.
soit:
observés
xi et yi pour chaque paire i, avec i=1,2,...,i,...n
estimer
B1,B2,...,Bj,..,Bk et (Y1,Y2,...,Yi,...,Yn) pour les n paires de valeurs observées.
(Valeurs estimées =
1,
2,...,
j,...,
k ou b1,b2,...,bj,...,bk et
1,
2,...,
i,...,
n)
Fonction objet ou fonction critère
Critère d’estimation
Les estimateurs seront les valeurs de Bj qui minimisent la fonction objet.
(Ce critère est dénommé méthode des moindres carrés).
Version matriciel
Il convient présenter le problème en utilisant des matrices et en appliquant le calcul matriciel.
Ainsi:
Vecteur X(n,1) = Vecteur des valeurs observées de la variable auxiliaire
Vecteur y(n,1) = Vecteur des valeurs observées de la variable réponse
Vecteur Y(n,1) = Vecteur des valeurs de la variable réponse obtenu par le modèle.
Vecteur B(k,1) = Vecteur des paramètres
Vecteur b(k,1) = Vecteur des estimateurs des paramètres
Modèle
Y(n,1) = f(X; B)
Fonction objet
F(1,1) = (y-Y)T.(y-Y)
Dans le cas du modèle linéaire le système d’équations résultantes de l’égalisation à zéro de la dérivée de la fonction F à l’ordre du vecteur B n’est généralement pas simple à résoudre. L’estimation par la méthode des moindres carrés pourra, cependant, être effectuée en recourant à quelques modifications qui ont pour base le développement de la fonction Y en série de Taylor, comme une approximation au modèle.
Révision du développement Taylor
On peut exemplifier le développement d’une fonction en série de Taylor en utilisant le cas le plus simple d’une fonction à une variable.
L'approximation de Taylor se traduit par le développement d’une fonction Y = f(x) autour d’un point sélectionné, x0 , en série de puissances de x:
Y = f(x) = f(x0) +(x-x0).f’(x0)/1! + (x-x0)2f’’(x0)/2! +... + (x- x0)i f(i)(x0)/i!+...
où
f(i)(x0) = dérivées de f(x) à l’ordre de i, au point x0.
Le développement se rapproche jusqu’à la puissance voulue. Quand le développement est rapproché à la puissance 1 on dit qu’il s’agit de l’approximation linéaire de Taylor, soit,
Y = f(x0) + (x-x0).f’(x0)
Le développement de Taylor peut s’appliquer à des fonctions de plus d’une variable. Par exemple, pour une fonction Y = f(x1,x2), le développement linéaire serait:
qui, en langage matriciel peut s’écrire ainsi:
Y = Y(0)+A(0).(x-x(0))
où Y(0) est la valeur de la fonction au point x(0) de composants (x1-x1(0)) et (x2-x2(0)) et A(0) est la matrice de dérivées à composants égaux à la dérivée partielle de f(x1,x2) à l’ordre de x1,x2 au point (x1(0), x2(0)).
Dans le cas de l’estimation de paramètres le développement de la fonction Y en série de Taylor est réalisé à l’ordre des paramètres B et non pas au vecteur X.
Par exemple, le développement linéaire de Y = f(x,B) à l’ordre de B1, B2,..., Bk , serait:
Y = f(x;B) = f(x; B(0)) + (B1-B1(0)) ¶f /¶B1 (x;B(0)) +..... +
(B2-B2(0)) ¶ f /¶B2 (x;B(0)) +...... +..........+ (Bk-Bk(0)) ¶f /¶Bk (x;B(0))
ou, en langage matriciel:
Y(n) = Y(0) + A(0).DB(0)
où
A = matrice d’ordre (n,k) des dérivées partielles de la matrice f(x;B) par rapport au vecteur B au point B(0) et
DB(0) = vecteur (B - B(0)).
Alors la fonction objet sera:
F = (y-Y)T.(y-Y) = (y-Y(0) - A(0). DB(0))T(y-Y(0) - A(0). DB(0))
Pour obtenir le minimum de cette fonction il convient mieux de dériver F par rapport au vecteur DB au lieu du vecteur B et égaler à zéro. Ainsi, on aura:
0 = -2(A(0))T(y-Y(0) -A(0). DB(0)) = -2A(0)T(y-Y(0))+ 2A(0)TA(0). DB(0)
ou
A(0)TA(0). DB(0) = A(0)T(y-Y(0))
et, donc, on aura:
Si le vector DB(0) est “égal à zéro” c’est que l’estimateur de B est égal à B(0).
(il convient de préciser que, dans la pratique, quand on dit "égal à zéro" dans ce processus, on veut dire "plus petit que approx" où approx est le vecteur d’approximation que l'on voulait définir).
Dans le cas contraire la nouvelle valeur de B sera:
B(1) =B(0) + DB(0)
et le processus se répétera, c’est-à-dire que l’on procédera à une nouvelle itération avec B(0) substitué par B(1) (et A(0) substitué par A(1)). Le processus itératif continuera jusqu'à ce que la convergence voulue soit vérifiée.
Commentaires
1. Il n'est pas dit que le processus converge toujours. Quelques fois il ne converge pas, d'autres fois il est trop lent (même pour les ordinateurs!) et d'autres encore il converge mais vers une autre limite !!
2. La méthode qui a été décrite précédemment est la méthode de Gauss-Newton qui est la base de plusieurs autres méthodes. Quelques-unes de ces méthodes introduisent des changements pour obtenir une convergence plus rapide comme dans de cas de la méthode de Marquardt (1963), assez utilisée en recherche halieutique. D'autres méthodes utilisent le développement de Taylor de deuxième ordre (méthode de Newton-Raphson), cherchant ainsi une meilleure approximation. D'autres encore conjuguent deux changements.
3. Ces méthodes nécessitent que l’on calcule des dérivées des fonctions. Quelques logiciels demandent l'introduction des expressions mathématiques des dérivées, d'autres utilisent des sous-routines avec des approximations numériques des dérivées.
4. Il faut aussi souligner que les méthodes existantes dans la recherche halieutique et étudiées dans ce cours pour calculer les valeurs de divers paramètres, comme par exemple, croissance, mortalités, courbes de sélectivité et de maturation, peuvent fournir des valeurs initiales pour les paramètres au cas ou l'on prétendrait utiliser des méthodes itératives dans les modèles non-linéaires.
5. De toute façon il est important de faire ressortir un aspect commun aux méthodes itératives: la valeur initiale du vecteur B(0) utilisé dans le processus doit être choisie le plus proche possible de la vraie valeur. Ainsi, non seulement la convergence est plus rapide mais il est aussi plus sûr qu'elle finira dans la limite voulue.
La méthode des moindres carrés
(régression non-linéaire) permet l'estimation des
paramètres K, L et
to des équations de croissance individuelle.
et
to des équations de croissance individuelle.
Les valeurs initiales de K, L et t0 peuvent être obtenues
à travers de la régression linéaire simple en utilisant les
méthodes suivantes:
et t0 peuvent être obtenues
à travers de la régression linéaire simple en utilisant les
méthodes suivantes:
Méthodes de Ford-Walford (1933-1946) et de Gulland et Holt (1959)
Les expressions de Ford-Walford et de Gulland et Holt, qui ont
été présentées dans la Section 3.4, se trouvent
déjà dans leur forme linéaire, permettant ainsi
l'estimation des valeurs initiales de K e L par des méthodes de régression
linéaire simple. L'expression de Gulland et Holt permet l'estimation de K
et L
par des méthodes de régression
linéaire simple. L'expression de Gulland et Holt permet l'estimation de K
et L même quand les intervalles
de temps Ti ne sont pas constants. Dans ce cas il convient de
réécrire l'expression comme:
même quand les intervalles
de temps Ti ne sont pas constants. Dans ce cas il convient de
réécrire l'expression comme:
DL/TI = K.L
- K.
Méthode de Stamatopoulos et Caddy (1989)
Ces auteurs présentent aussi une méthode pour
évaluer K, L et to
(ou L0) en utilisant la régression linéaire simple.
Pour cela l'équation de von Bertalanffy est exprimée comme une
relation linéaire de Lt contre e-Kt.
et to
(ou L0) en utilisant la régression linéaire simple.
Pour cela l'équation de von Bertalanffy est exprimée comme une
relation linéaire de Lt contre e-Kt.
Considérez ainsi n paires de valeurs ti, Li où ti est l'âge et Li la longueur de l'individu i avec i=1,2,...., n.
L'équation de von Bertalanffy, dans sa forme générale, est comme on l'a déjà vu:
L
- Lt = (L
- La). e-K(t-ta)
Qui peut être écrite sous la forme:
Lt = L
- (L
- La). e+Kta. e-Kt
Comme on peut le voir, l'équation antérieure est de forme linéaire simple, y = a + bx, où:
|
y = Lt |
a = L |
b = - (L |
x = e-Kt
Si l'on adopte La = 0 on aura ta=to, mais en contrepartie si l'on adopte ta = 0 on aura La = Lo.
De toute façon les paramètres à
évaluer à partir de a et b seront L , to ou Lo.
, to ou Lo.
Ainsi les auteurs proposent l'adoption d'une valeur de K, soit, K(0), et par régression linéaire simple entre y (= Lt) et x(=e-Kt) évaluer a(0), b(0) et r2(0). La procédure peut être répétée pour diverses valeurs de K, soit, K(1) K(2),.... On pourra alors adopter la régression qui résulte dans la plus grande valeur de r2, à laquelle correspondra Kmax et amax et bmax. Ces valeurs de amax, bmax et Kmax permettront l'obtention des valeurs des paramètres restants.
Un processus pratique pour trouver Kmax pourra être:
(i). Sélectionner deux valeurs extrêmes de K qui incluent la valeur prétendue, par exemple K= 0 et K=2 (pour des difficultés pratiques utiliser K = 0.00001 au lieu de K = 0).
(ii). Calculer les 10 régressions pour des valeurs de K comprises entre ces deux valeurs en intervalles égaux.
(iii). Les 10 valeurs correspondantes de r2 obtenues permettront de sélectionner deux nouvelles valeurs de K qui déterminent un autre intervalle plus petit que celui de (i) contenant la valeur de r2 maximum obtenue.
(iv). Les étapes (ii) et (iii) peuvent se répéter jusqu'à l'obtention de valeurs de K avec l'approximation voulue. Généralement cette étape ne nécessite pas beaucoup de répétitions.
Diverses méthodes ont été proposées pour évaluer M, qui se basent sur l'association de M avec d'autres paramètres biologiques de la ressource. Ces méthodes produisent des résultats rapprochés, où les rapprochements dépendent des espèces et des stocks.
7.5.1 RELATION DE M AVEC LA LONGEVITE,
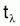
Longévité: Âge maximum moyen des individus de la population du stock non-exploité.
Durée de la vie exploitable:
 (Figure 7.1)
(Figure 7.1)
Figure 7.1 Durée de la vie exploitable

Tanaka (1960) propose des Courbes de Survie "NATURELLE" (Figure 7.2) pour obtenir des valeurs de M à partir de la longévité.
Dans les cas pratiques on peut considérer qu'une
cohorte s'éteint quand seulement une fraction, p, des individus
recrutés survit. Dans ce cas, en partant de
 , on peut
écrire:
, on peut
écrire:
p =
et donc
M = -(1/l).ln p
Différentes valeurs de la fraction p de survie produisent différentes courbes de survie.
Figure 7.2 Courbes de survie de Tanaka

Le choix de la valeur de p est arbitraire, mais adopter p = 5% (i.e. une recrue sur vingt survit jusqu'à l'âge tl) comme valeur variable.
7.5.2 RELATION ENTRE M ET CROISSANCE
Méthode de Beverton et Holt (1959)
Gulland (1969) mentionne que Beverton et Holt ont vérifié que des espèces avec un taux de mortalité M supérieur présentent aussi des valeurs de K supérieures. En cherchant une relation simple entre ces deux paramètres, ils ont conclu que, approximativement, on pourrait affirmer que:
|
|
pour les petits pélagiques |
|
|
pour les poissons de fond |
Méthode de Pauly (1980)
En se basant sur les considérations suivantes:
a) les ressources avec un taux de mortalité élevé ne peuvent pas avoir une longueur maximum très grande;
b) dans les eaux chaudes, le métabolisme est plus accéléré, d'où la possibilité d'atteindre une taille plus élevée et la longueur maximum plus rapidement qu'en eaux plus froides.
Pauly a recueilli, dans la littérature, des
données sur ces paramètres, pour 175 espèces et a
ajusté des régressions multiples de valeurs transformées de
M contre les valeurs transformées correspondantes de
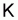 ,
,
 et de température,
de façon à trouver une relation linéaire et il a
sélectionné celle qu'il a considéré comme la
meilleure, soit la relation empirique suivante:
et de température,
de façon à trouver une relation linéaire et il a
sélectionné celle qu'il a considéré comme la
meilleure, soit la relation empirique suivante:
avec les paramètres exprimés dans les unités suivantes:
M = an-1
= cm de longueur totale
K = an-1
température à la surface des eaux en
Pauly attire l'attention sur les soins à apporter dans l'application de cette expression à des petits pélagiques et crustacés. La relation de Pauly, en utilisant des logarithmes décimaux, présente le premier coefficient différent de la valeur -0.0152 donné dans l'expression antérieure, écrite avec des logarithmes népériens.
7.5.3 RELATION ENTRE M ET REPRODUCTION
Méthode de Rikhter et Efanov (1976)
Ces auteurs ont analysé la dépendance entre M et l'âge de 1ère maturation à partir de données représentatives d'espèces ayant une durée de vie courte, moyenne et longue, en trouvant une dépendance de M avec l'âge de 1ère maturation et l'ont transformée en l'expression empirique suivante:
|
|
(Unités) |
|
|
|
Méthode de Gundersson (1980)
En se basant sur la supposition que le taux de mortalité naturelle devra être en relation avec l'investissement des poissons dans la reproduction, au-delà de l'influence d'autres facteurs, Gundersson a établi diverses relations entre M et ces facteurs.
Il a proposé, cependant, la relation empirique suivante, simple, en utilisant l'Indice Gonadosomatique (IGS) (estimé pour des femelles matures à l'époque de frai) pour obtenir une évaluation de M:
7.5.4 DONNÉ LA STRUCTURE PAR ÂGE DU STOCK, AU DÉBUT ET À LA FIN DE L'ANNÉE, ET LES CAPTURES EN NOMBRE PAR ÂGE PENDANT CETTE ANNÉE
On peut calculer les coefficients de mortalité naturelle Mi pour chaque âge i et pendant l'année comme:
|
calculer |
|
|
calculer |
|
|
calculer |
|
Les diverses valeurs de M obtenues à chaque âge pourront être comparées et probablement combinées pour calculer une valeur constante, M, pour tous les âges.
Méthode de Paloheimo (1961)
Quand  et
et
 sont connus pour plusieurs
années i, et en supposant
sont connus pour plusieurs
années i, et en supposant
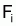 proportionnel à
proportionnel à
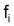 ,
,
pour
an,
,
alors:
Ainsi, la régression linéaire entre
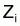 et
et
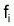 a une pente
a une pente
 et une intersection
et une intersection
 .
.
Il existe plusieurs méthodes pour évaluer le coefficient de mortalité total, Z, supposé constant pendant un certain intervalle d'âge ou d'année.
Il convient de grouper les méthodes suivant les cas où les données de base sont relatives à des âges ou à des longueurs.
7.6.1 MÉTHODES AVEC DES DONNÉES PAR ÂGES
Les différentes méthodes ont comme point de départ l'expression générale du nombre de survivants d'une cohorte, à l'instant t, soumise à la mortalité totale, Z, pendant un intervalle de temps, soit:
pour l'intervalle de temps (ta,tb) où Z est supposé constant.
En logarithmisant cette expression et en réarrangeant les termes on aura:
lnNt = Cte - Z.t
où Cte est constant (= ln Na+Zta).
Cette expression montre que le logarithme du nombre de survivants est linéaire avec l'âge, la pente étant égale à -Z.
(la Cte n'a aucun intérêt spécial pour la détermination de Z. Il faut ajouter que les expressions constantes dans toute expression qui ne présente pas d'intérêt pour la détermination de Z seront indiquées par Cte).
Si, dans l'intervalle
(ta,tb), Z peut être
considéré constant et, si l’on dispose de données
d'abondance, 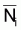 , ou d'indices
d'abondance en nombre,
, ou d'indices
d'abondance en nombre, 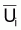 ,
pour plusieurs âges, i, alors l'application de la technique de
régression linéaire simple permet l'estimation du coefficient de
mortalité total Z.
,
pour plusieurs âges, i, alors l'application de la technique de
régression linéaire simple permet l'estimation du coefficient de
mortalité total Z.
En effet
donc
= Ni. Constante
et, comme
alors, en substituant, on aura:
(Ti = const = 1 an)
et, donc, on aura aussi
et la régression linéaire simple entre
 et ti permet
d’évaluer Z (notez que la constante, Cte, est différente de
la précédente mais à cet effet seule la pente
intéresse pour évaluer Z).
et ti permet
d’évaluer Z (notez que la constante, Cte, est différente de
la précédente mais à cet effet seule la pente
intéresse pour évaluer Z).
Au cas où les âges ne sont pas à intervalles constants, l'expression pourra être exprimée en utilisant les valeurs tcentrali , de forme rapprochée.
Pour Ti variable on aura:
» Ni. e-ZTi/2
et, comme
Ni = Na. e -Z.(ti-ta)
on aura
» Cte. e-Ztcentrali
et, finalement:
» Cte - Z. tcentrali
Dans le cas des indices
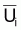 la situation est semblable
car
la situation est semblable
car 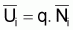 , avec q constant, et,
donc, on aura aussi:
, avec q constant, et,
donc, on aura aussi:
et la régression linéaire simple entre
 et ti permet
d’évaluer Z.
et ti permet
d’évaluer Z.
Au cas où les âges ne seraient pas à intervalles constants l'expression devra être modifiée et sera:
» Cte - Z. tcentrali
Avec des données de captures, Ci , et
âge, ti , il est toujours possible d’appliquer la
régression linéaire simple pour obtenir Z, mais dans ce cas, il
faudra supposer que Fi est constant. Rappelez-vous que Ci
= Fi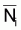 Ti et ainsi,
lnCi = Cte +
Ti et ainsi,
lnCi = Cte +  quand Ti est constant. Donc:
quand Ti est constant. Donc:
lnCi = Cte - Z. ti
Au cas où les âges ne sont pas séparés par des intervalles constants l'expression devra être modifiée et sera:
lnCi/Ti » Cte - Z. tcentrali
On désigne par Vi la capture accumulée dès ti jusqu'à la fin de la vie (forme qui convient pour les calculs des diverses captures accumulées) soit:
Vi = SCk = SFk Nkcum,
où la somme s'étend dès le dernier âge jusqu'à l'âge i.
Comme Fk et Zk sont supposés être constants SNkcum = Ni/Z et donc, on aura:
Vi = FN/Z
et
lnVi = Cte + lnNi
Donc:
ln Vi = Cte - Z. ti
Finalement on mentionnera que Beverton et Holt (1956) ont aussi montré que:
et, donc, il est possible d’évaluer Z
à partir de l'âge moyen
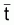
(cette expression a été obtenue en
considérant tb =  dans l'intervalle (ta, tb)).
dans l'intervalle (ta, tb)).
7.6.2 MÉTHODES AVEC DES DONNÉES PAR LONGUEUR
Quant au lieu de données par âge on dispose de données par classe de longueur, les méthodes citées précédemment peuvent être appliquées, mais pour cela il faut définir âge relatif.
En utilisant l'équation de von Bertalanffy on peut obtenir l'âge t en fonction de la longueur, comme:
(l'expression doit être écrite sous sa forme générale par rapport à ta et non pas à t0)
t = ta - (1/K).ln[(L
- Lt)/(L
- La)]
(Cette équation est mentionnée par quelques auteurs comme l'équation inverse de von Bertalanffy).
On nomme âge relatif, t*, la différence t-ta.
Ainsi: t* =-(1/K).ln[(L - Lt)/(L
- Lt)/(L - La)]
=-(1/K)ln[1-(Lt-La)/ (L
- La)]
=-(1/K)ln[1-(Lt-La)/ (L - La)]
- La)]
pour t = ta serait La = 0 et:
En effet, cet âge est relatif car il diffère de l'âge absolu par une quantité constante, ta.
Ainsi, par exemple, la durée de l'intervalle Ti peut être calculée par la différence des âges absolus des extrêmes de l'intervalle, comme par la différence des âges relatifs:
Ti = ti+1 -ti = t*i +1 - t*i
et cet intervalle correspond au temps que l'individu met à grandir entre Li et Li+1, Ti étant la taille de l'intervalle i. De même:
t*centrali = tcentrali + Cte
Ainsi les expressions précédentes sont maintenues quand on substitue les âges absolus par des âges relatifs:
= Cte - Z. t*centrali
= Cte - Z. t*centrali
ln Vi = Cte - Z. t*i
ln Ci/Ti = Cte - Z. t*centrali
Finalement, on aura également:
Mais Beverton et Holt (1957) on prouvé que:
(Rappelez-vous que
 doit être
calculé comme la moyenne des valeurs de Li prises en
considération avec les abondances (ou indices) ou avec les
captures).
doit être
calculé comme la moyenne des valeurs de Li prises en
considération avec les abondances (ou indices) ou avec les
captures).
Commentaires
1. L'application d'une quelconque de ces méthodes doit être précédée de la représentation graphique des données correspondantes, afin de vérifier si les suppositions des méthodes sont acceptables ou non, et, aussi, pour déterminer l'intervalle d'intérêt, (ta , tb).
2. Les démonstrations de ces formules sont immédiates (avec les indications qui sont présentées), mais il est intéressant de développer les démonstrations car elles permettent d’expliciter les suppositions qui rendent les méthodes applicables.
3. L'estimation de Z constant devra toujours être tentée, même quand ce n'est pas acceptable, car cela sert d'orientation sur la grandeur des valeurs que l'on peut espérer.
4. Les méthodes sont citées dans la littérature, parfois avec les noms des auteurs qui les ont appliquées pour la première fois. Par exemple, l'expression ln Vi = Cte - Z.t*i est appelée méthode de Jones et van Zalinge (1981).
5. L'âge moyen de même que la longueur moyenne dans la capture peuvent être obtenus par les expressions suivantes:
avec Ci = capture en nombre à l'âge i
avec Ci = capture en nombre dans la classe de longueur i
avec Ci = capture en nombre dans la classe d'âge i
L'âge relatif devra être t* = -
(1/K).ln[(L -
Lt)/(L
-
Lt)/(L -
La)]
-
La)]
FORMULAIRE - Estimation du Coefficient de Mortalité Total, Z
|
Supposition: Z constant dans l'intervalle d'âges, (ta, tb) |
||
|
T Constant |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ti variable |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Supposition: Z constant dans un intervalle de longueurs, (La, Lb) |
||
|
Âge relatif
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(équation de Jones et van Zalinge) |
|
|
|
|
La méthode des moindres carrés (modèle non-linéaire) peut être utilisée pour évaluer les paramètres, a et k, de quelque modèle S-R.
Les valeurs initiales du modèle de Beverton et Holt (1957) peuvent être obtenues en réécrivant l'équation sous la forme:
(R/S)-1 ou
et en estimant la régression linéaire simple entre y (= S/R) et x (=S) qui donnera les estimations de 1/a et de 1/aK. À partir de ces valeurs on pourra alors évaluer les paramètres (a et K) du modèle de Beverton et Holt, qui pourront être considérés comme valeurs initiales dans l'application du modèle non-linéaire de Beverton et Holt.
Dans le cas du modèle de Ricker (1954) les paramètres peuvent être obtenus en réécrivant l'équation sous la forme:
et en évaluant la régression linéaire simple entre y (= ln R/S) et x (=S) qui donnera les estimations de lna et de (-1/k). À partir de ces valeurs on pourra évaluer aussi les paramètres (a et k du modèle, qui pourront être considérés comme valeurs initiales dans l'application du modèle non-linéaire de Ricker.
Il convient de représenter le graphique de y contre x de mode à vérifier si les points marqués s'ajustent à une droite avant d'appliquer la régression linéaire à l'un de ces modèles.
Dans les modèles avec le paramètre c flexible, comme par exemple le modèle de Deriso (1980), l'équation pourra être réécrite comme:
La régression linéaire entre y (= (R/S)c) et x (=S) permet d’évaluer les paramètres a et k.
Diverses valeurs de c peuvent être essayées pour vérifier avec laquelle la droite y contre x s'ajustera meilleur, suggérant par exemples des valeurs de c entre -1 et 1.
À partir des valeurs ainsi obtenues pour a, k et c, qui pourront être considérées comme valeurs initiales dans l'application du modèle non-linéaire de Deriso, on pourra évaluer les paramètres a , k et c du modèle.
7.8.1 ANALYSE DE COHORTES PAR ÂGES - (AC)
L'analyse de cohortes est une méthode qui consiste en l'estimation des coefficients de mortalité par pêche, Fi, et du nombre de survivants, Ni, au début de chaque âge, à partir des structures des captures, en nombre, d'un stock pendant une période d'années.
Plus concrètement, considérez un stock duquel on connaît:
Données
âge, i, avec i = 1,2,...,k
an, j, avec j = 1,2,...,n
Matrice des captures [C] avec
Ci,j = Capture annuelle, en nombre, des individus d'âge i pendant l'année j
Matrice de mortalité naturelle [M] avec
Mi,j = coefficient de mortalité naturelle, à l'âge i pendant l'année j.
Vecteur [T] avec
Ti = Taille de l'intervalle de l'âge i (généralement, Ti=T=1 an)
Objectif
évaluer
matrice [F]
et
matrice [N].
Il convient, pour résoudre ce problème, de considérer séparément les estimations pour: un intervalle i d'âges, (partie 1), pour tous les âges pendant la vie d'une cohorte (partie 2) et, finalement, pour tous les âges et ans (partie 3).
PARTIE 1 (INTERVALLE TI)
Considérez connues les caractéristiques suivantes d'une cohorte, dans un intervalle Ti:
Ci = Capture en nombre
Mi = Coefficient de mortalité naturelle
Ti = Taille de l'intervalle
Si l'on adopte une valeur pour le coefficient Fi alors il est possible d'évaluer le nombre de survivants au début, Ni, et à la fin, Ni+1 , de l'intervalle.
A partir de l'expression:
on peut calculer Ni, qui est la seule variable inconnue de l'expression.
Pour calculer Ni+1 on peut utiliser
l'expression 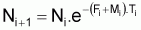 en utilisant
la valeur Ni calculée antérieurement
en utilisant
la valeur Ni calculée antérieurement
PARTIE 2 (PENDANT LA VIE)
On suppose maintenant que les captures Ci de chaque âge i d'une cohorte pendant sa vie, les valeurs de Mi et les tailles des intervalles Ti sont connues.
Si l’on admet une certaine valeur, Fult , pour la dernière classe d'âges, il est possible, comme indiqué dans la partie 1, d’évaluer tous les paramètres (numérotés) dans ce dernier âge. Ainsi on passe on connaîtra le nombre de survivants au début et à la fin du dernier âge.
Se rappeler que le nombre au début et à la fin de cette dernière classe d'âge, calculé comme dans le paragraphe précédent, est aussi le nombre à la fin de la classe précédente. Soit Nfinal le nombre de survivants à la fin de l'avant-dernière classe.
En utilisant l'expression connue:
on peut estimer Fi de la classe antérieure qui est la seule variable inconnue dans l'expression.
L'estimation peut nécessiter des méthodes itératives ou méthodes de tentative et erreur.
Finalement pour estimer Ni le nombre de survivants au début de la classe, on peut utiliser l'expression:
En répétant ce processus pour toutes les classes antérieures, on obtiendra successivement les paramètres à tous les âges, jusqu'au premier âge. Se rappeler que Ni est aussi le nombre de survivants de la classe (i-1) antérieure. Quand la cohorte est complètement pêchée, le nombre à la fin de la dernière classe est zéro et la capture C doit être calculée par:
Méthode de Pope
Pope (1972) a présenté une méthode simple qui permet d’évaluer le nombre de survivants au début de chaque âge de vie de la cohorte à partir du dernier âge.
Il suffit d'appliquer successivement et de la fin vers le début l'expression:
Pope indique que le rapprochement est bon quand MT £ 0.6
L'expression peut se dériver, selon Pope, en supposant que la capture est effectuée exactement au point central de l'intervalle Ti (Figure 7.3).
Figure 7.3 Évolution du nombre de survivants pendant Ti avec la capture extraite au point central de l'intervalle

Procédant de la fin vers le début on aura successivement:
par substitution de N’ par N’’+Ci, on aura:
Et, en substituant N’’ par Ni+1.e +MTi/2, sera:
Partie 3 (période d'années)
On suppose, finalement, que, pendant une période d'années, la matrice Capture [C], la matrice mortalité naturelle [M] et le vecteur taille des intervalles [T], où les lignes, i, sont des âges et les colonnes, j, sont des années sont connues.
On admet également que l'on adopte des valeurs de F dans les derniers âges de toutes les années représentées dans les matrices et les valeurs de F de tous les âges dans la dernière année. On désignera ces valeurs par Fterminal (Figure 7.4).
Figure 7.4 Matrice capture, [C], avec Fterminais dans la dernière ligne et dernière colonne de la matrice C. Les cellules ombragées indiquent les captures d'une cohorte
|
Années |
|||||
|
Âges |
2000 |
2001 |
2002 |
2003 |
|
|
1 |
C |
C |
C |
C |
Fterminal |
|
2 |
C |
C |
C |
C |
Fterminal |
|
3 |
C |
C |
C |
C |
Fterminal |
|
|
Fterminal |
Fterminal |
Fterminal |
Fterminal |
|
Notez que dans ces matrices les éléments en diagonale correspondent à des valeurs d'une même cohorte, puisque à un élément d'un âge et d'une année suivra, à la diagonale, l'élément plus une année d'âge et de l'année suivante, et, donc, l'élément suivant de la cohorte.
A partir de ce qui a été dit dans les parties 1 et 2 il sera alors possible d’évaluer Fs et Ns successivement pour toutes les cohortes présentes dans la matrice capture, soit, dans toutes les cellules.
Commentaires
1. Plusieurs fois, en pratique, il est courant d’adopter des valeurs Mi,j constantes et égales à M.
2. Quand les données se référent à des âges, les valeurs Ti ont pour habitude d’être toutes égales à 1 an.
3. Les derniers groupes de chaque année sont parfois des âges (+). Les captures correspondantes sont constituées par des individus pêchés pendant ces années, à cet âge ou à un âge supérieur. Ainsi, les valeurs accumulées n'appartiennent pas à la même cohorte, mais sont des survivants de plusieurs cohortes antérieures. Il ne serait pas légitime d’utiliser la capture d'un groupe (+) pour analyser la cohorte en référence, car ces autres cohortes résultent de différentes tailles de recrutement. À part cela, le groupe (+) est important dans le calcul des totaux annuels de capture en poids, Y, et biomasses totales, B, et de ponte, BP. Ainsi, il est courant d'analyser les cohortes à partir de l'âge immédiatement antérieur au groupe (+) et de n’utiliser le groupe (+) que pour des calculs de Y, B et BP. La valeur de F dans ce groupe (+) chaque année peut être évalué comme étant le même coefficient de mortalité par pêche de l'âge antérieur ou, dans quelques cas, une valeur raisonnable par rapport aux valeurs de Fi dans l'année en question.
4. Une difficulté dans l'application de la technique AC surgit quand le nombre d'âges est petit ou quand il y a peu d'années. En effet, dans ces cas, les cohortes ont peu de classes d'âges représentées dans la matrice [C] et les estimations seront très dépendantes des valeurs adoptées de Fterminal.
5. L'analyse de cohortes (AC) est aussi désignée par d'autres noms: VPA (Virtual Population Analysis), méthode de Derzhavin, méthode de Murphy, méthode de Gulland, méthode de Pope, Analyse Séquentielle, etc. Parfois on se réfère à AC quand on utilise la formule de Pope et VPA dans les autres cas. Megrey (1989) présente une révision très complète sur l'analyse de cohortes.
6. Il est aussi possible d’évaluer les
paramètres restants à un âge i, se rapportant
à des nombres, soit, Ncumi,
 , Di,
Zi et Ei. Avec des informations sur le poids
individuel initial ou moyen, matrice [w] ou matrice [w], on peut aussi calculer
les captures annuelles en poids [Y], les biomasses au début des
années, [B] et les biomasses moyennes pendant les années
, Di,
Zi et Ei. Avec des informations sur le poids
individuel initial ou moyen, matrice [w] ou matrice [w], on peut aussi calculer
les captures annuelles en poids [Y], les biomasses au début des
années, [B] et les biomasses moyennes pendant les années
 . Avec des informations sur
les ogives de maturation chaque année, par exemple, au début de
l'année, on peut aussi calculer les biomasses de ponte, [BP].
Normalement, on estime seulement les captures totales Y, les biomasses du stock
(totales et de ponte) au début et les biomasses moyennes du stock
(totales et de ponte) chaque année.
. Avec des informations sur
les ogives de maturation chaque année, par exemple, au début de
l'année, on peut aussi calculer les biomasses de ponte, [BP].
Normalement, on estime seulement les captures totales Y, les biomasses du stock
(totales et de ponte) au début et les biomasses moyennes du stock
(totales et de ponte) chaque année.
7. Les éléments de la première ligne de la matrice [N] peuvent être considérés des estimations du recrutement à la pêche chaque année.
8. Le fait d'adopter Fterminal et par ces valeurs influencer les résultats - matrice [F] et matrice [N] - oblige à sélectionner des valeurs de Fterminal proches des vrais. La cohérence entre les estimations des paramètres mentionnés dans les points 6 et 7 et d'autres données ou indices indépendants (par exemple, estimations par des méthodes acoustiques de recrutement ou biomasses, estimations d'indice d'abondance ou cpue, d'effort de pêche, etc.) doit être analysée. Ces vérifications sont obligatoires pour valider l'analyse de cohortes (parfois on utilise incorrectement les désignations calibrage ou syntonisation, expressions qui prétendent traduire le terme anglais "tuning", au lieu de validation).
9. Un autre aspect des matrices résultantes de l'AC et la possibilité de vérifier et d’évaluer l'hypothèse de séparer le niveau de pêche de chaque année et le régime d'exploitation de chaque âge, c’est-à-dire de transformer les Fij calculés dans chaque cellule du produit Fj.si, soit Fi,j = Fj.si, avec i = âge et j = an.
On a l’habitude de désigner cette séparation comme VPA-Séparable (SVPA).
Soit
et
et
Ainsi, si  on peut prouver que
on peut prouver que
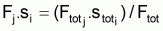 .
.
Si les valeurs estimées pour Fi,j sont égales aux valeurs antérieures, qui ont été désignées par Fsepij = Fj.si, alors l'hypothèse est vérifiée. Cette comparaison peut être réalisée de diverses manières mais, la plus simple, sera probablement, de calculer les quotients (Fsepij/Fij) qui, au cas où l'hypothèse serait vraie devront être égaux à 1. Notez que si l'hypothèse n'est pas vérifiée il sera toujours possible de considérer d'autres hypothèses de façon à ce que le vecteur annuel [s] soit constant seulement en quelques années, surtout ces dernières années.
10. De toute façon on a l’habitude de
considérer un intervalle d'âges, où il est supposé
que les individus capturés sont "complètement recrutés". Si
l'intervalle d'âges correspond à des individus complètement
recrutés il faut espérer que le régime d'exploitation
calculé se rapproche de 1 (pour les âges restants qui ne sont pas
complètement recrutés le régime d'exploitation devra
être inférieur à 1). Pour cet intervalle d'âge, i, on
calcule alors la moyenne des valeurs de Fi,j à chaque
année. Ces moyennes,
 , sont
considérées comme niveau de pêche dans les années
respectives. Le régime d'exploitation dans chaque cellule, serait alors
le quotient Fi,j
/
, sont
considérées comme niveau de pêche dans les années
respectives. Le régime d'exploitation dans chaque cellule, serait alors
le quotient Fi,j
/ .
.
7.8.2 ANALYSE DE COHORTES PAR LONGUEURS - (LCA)
La technique d'analyse de cohortes, appliquée à la structure des captures d'une cohorte pendant sa vie peut être effectuée avec des intervalles de temps, Ti, non constants. Cela signifie que si l'on dispose de la structure des captures d'une cohorte pendant sa vie, en classes de longueurs, on peut aussi “analyser la cohorte”.
Les méthodes de procédure de l'analyse de cohortes dans ces cas se dénomment LCA (Length Cohort Analysis en anglais). Les mêmes techniques, méthode de Pope, méthode itérative, etc, de l'AC pour des âges, peuvent être appliquées dans l'analyse LCA (rappelez-vous que les intervalles Ti´s peuvent être calculés à partir des âges relatifs).
Un mode d'appliquer LCA à la composition de captures, par longueurs, sera grouper, antérieurement, les captures dont les classes de longueur appartiennent à un même intervalle d'âges, obtenant ainsi la composition des captures par âges. La technique AC peut alors être appliquée directement à la matrice [C]. Cette technique est connue par “couper en tranches”, (slicing en anglais) la composition par longueurs. Pour "couper en tranches" une composition par longueurs il est coutume invertir l'équation de croissance en longueur de von Bertalanffy et d’évaluer l'âge ti pour chaque longueur Li (parfois on utilise des âges relatifs t*i) (Figure 7.5). Alors, la capture dans un certain groupe d'âge i sera obtenue en groupant les captures observées dans les classes de longueur comprises entre les deux âges extrêmes de l'intervalle d'âges respectif. Il peut arriver que les classes de longueurs qui sont constituées par des éléments qui appartiennent à deux groupes d'âges consécutifs. Dans ce cas il faudra répartir la capture de ces classes extrêmes en deux parties et les attribuer à chacun de ces âges. Dans l'exemple de la Figure 7.5, les captures de la classe de longueurs (24-26] appartiennent à l'âge 0 et à l'âge 1. Ainsi, il faut répartir cette capture par les deux âges. Une méthode simple pourra être attribuée à l'âge 0 la fraction (1.00 - 0.98)/(1.06 - 0.98) = 0.25 et à l'âge 1 la fraction (1.06 - 1.00)/(1.06 - 0.98) = 0.75 de la capture annuelle de cette classe de longueurs. La méthode ne sera pas la plus appropriée puisqu'elle se base sur la supposition que dans les classes de longueurs la distribution des exemplaires par longueur est uniforme. Pour cela, il conviendra, quand on applique cette technique de répartition, d’utiliser le plus petit intervalle de classes possible.
Une autre façon de réaliser l'analyse de cohortes par longueurs pourra être de ne pas grouper les captures dans les classes de longueur comprises dans le même groupe d'âges, mais les utiliser séparément. Les cohortes pourront être suivies dans la matrice [C], à travers des classes de longueurs appartenant à un même âge, dans une certaine année, avec les classes de longueurs de l'âge suivant, de l'année suivante, etc. Ainsi les différentes cohortes existantes dans la matrice seront séparées et l'évolution de chacune d'elles se présentera, non par âges, mais par classes de longueur (voir Figure 7.5).
Figure 7.5 Exemple d'une matrice [C] avec des classes de longueurs, "coupées en tranches", signalant en gras l'évolution d'une cohorte
| Groupe |
Années |
|||||
| Âge |
Âge relatif |
Classes |
2000 |
2001 |
2002 |
2003 |
|
0 |
1.03 |
20- |
41 |
30 |
17 |
49 |
| 1.54 |
22- |
400 |
292 |
166 |
472 |
|
| 1.98 |
24- |
952 |
699 |
400 |
1127 |
|
|
1 |
2.06 |
26- |
1766 |
1317 |
757 |
2108 |
| 2.30 |
28- |
2222 |
1702 |
985 |
2688 |
|
| 2.74 |
30- |
2357 |
1872 |
1093 |
2902 |
|
| 2.88 |
32- |
2175 |
1091 |
1067 |
2739 |
|
|
2 |
3.00 |
34- |
1817 |
948 |
1416 |
1445 |
| 3.42 |
36- |
1529 |
812 |
1270 |
1250 |
|
| 3.64 |
38- |
1251 |
684 |
980 |
1053 |
|
| 3.83 |
40- |
1003 |
560 |
702 |
710 |
|
| 3.96 |
42- |
787 |
290 |
310 |
558 |
|
|
3 |
4.01 |
44- |
595 |
226 |
179 |
834 |
| 4.25 |
46- |
168 |
70 |
71 |
112 |
|
| Cohorte de l'an 2000 |
||||||
La méthode LCA de Jones (1961), pour analyser une composition de longueurs pendant la vie d'une cohorte, pourra alors être appliquée. Cette méthode analyse une cohorte pendant la vie, constituée par les captures en classes de longueur en appliquant les méthodes déjà étudiées de l'AC avec des Ti non-constants. Les valeurs de Ti sont calculées comme Ti = ti+1*-ti*, où ti* et ti+1* sont les âges relatifs correspondants aux extrêmes de l'intervalle de longueur i. Le vecteur [N] obtenu sera constitué par le nombre de survivants initiaux dans chaque classe de longueur de la cohorte et non dans chaque classe d'âge.
Commentaires
1. Certains modèles, dénommés modèles intégrés, considèrent toute l'information disponible (captures, données des campagnes scientifiques, données d'effort, de rendement, etc.) qui avec la matrice [C], sont intégrés dans un seul modèle pour optimiser la fonction critère définie précédemment.
2. Fry (1949) a considéré les captures, par âges, accumulées de la fin vers le début, d'une cohorte pendant la vie comme image virtuelle du nombre de survivants au début de chaque âge (que l'auteur a désigné par “population virtuelle”):
Dans la pêcherie étudiée par Fry, M était pratiquement nul. Mais si M est différent de zéro on peut dire que le nombre Ni de survivants au début de l'intervalle i sera:
où Dk représente le nombre total de morts dans l'intervalle k.
En adoptant pour les taux d'exploitation, E, les valeurs initiales, Ek(0) , dans toutes les classes, on calcule:
N i(0) peut être calculé comme la valeur accumulée des morts totales, soit:
Alors, on aura:
et on peut calculer:
Les nouvelles valeurs de E seront:
Si l’on compare Ei(1) avec Ei(0) on peut évaluer, de la même façon que pour les méthodes itératives, les valeurs de E avec le rapprochement voulu.
Se rappeler que, dans la dernière classe le nombre, Nfinal , est égal au nombre de morts, Dfinal, et peut être calculé comme:
3. Finalement, il faut noter que les résultats de l'AC et de LCA nous donnent une perspective de l'histoire du stock dans les années antérieures. Cette information est, comme on l'a déjà vu, utile pour la réalisation de prévisions à Court et Long Terme. Normalement l'année ou l'on fait les évaluations les données de captures relatives à cette année ne sont pas encore disponibles, ce qui fait que l'on doit prévoir les captures et les biomasses pour l'année en cours avant d'effectuer les prévisions à Court Terme.
4. Quand on calcule les âges relatifs, on a l’habitude, pour uniformiser, d’adopter l'âge initial ta comme étant zéro. La valeur de La correspondante sera alors la limite inférieure de la première classe de longueurs représentée dans les captures.