1. Calculez:
|
A) |
|
|
|
|
|
||||
|
B) |
|
|
|
|
|
||||
|
C) |
|
|
|
|
|
||||
|
D) |
|
|
|
|
|
||||
|
E) |
|
|
|
|
|
|
|
|
|
2. Vérifiez que
|
a)
|
b)
|
|
c) |
d) |
3. Développez les expressions suivantes en appliquant des logarithmes (naturels) aux deux membres de l’égalité:
|
a)
|
b)
|
c)
|
Note: a, b, et c sont constants; e
est la constante de Neper 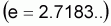 ;
x et y sont des variables.
;
x et y sont des variables.
4.Déterminez la valeur de x dans les expressions suivantes:
|
a)
|
b)
|
c)
|
5. Calculez les dérivées des expressions suivantes:
|
a) y=13 |
g) y=5x |
m) y=(4+2.x)3 |
|
b) y=3-8.x |
h) y=e-3·x |
n) y=(x-6)2 |
|
c) y=x5 |
i) y=ln x |
o) y= a.(3-e-b·x)3 |
|
d) y=x2/7 |
j) y=ln(5.x+4) |
p) y= (4.x+3).(ex-4) |
|
e) y=x-3 |
k) y= 1/x |
|
|
f) y=e3·x |
l) y= (2+4.x)/(3-x) |
|
6. Calculez les Primitives des expressions suivantes:
|
a)
|
f)
|
k)
|
|
b)
|
g)
|
l)
|
|
c)
|
h)
|
m)
|
|
d)
|
i)
|
n)
|
|
e)
|
j)
|
o)
|
7. Calculez l’aire sous la fonction
a)
entre
et
b)
entre
et
c)
entre
et
d)
entre
et
8. Calculez la valeur de
 avec
avec
a).
entre
et
b).
entre
et
c).
entre
et
9. Calculez la Valeur Moyenne de
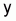 avec
avec
a).
entre
et
b).
entre
et
c).
entre
et
10. Calculez l’intégrale de
a).
à la condition initiale
où
b).
à la condition initiale
c).
à la condition initiale
d).
à la condition initiale
(cf. 2.2)
Considérez la fonction
 , dans l’intervalle
(0,10)
, dans l’intervalle
(0,10)
1. Calculez:
a). Les valeurs de y pour
;
b). Représentez graphiquement la fonction y dans l’intervalle (0,10) de x;
c). La variation,
, correspondante à l’intervalle (1.2) de x;
d). Les taux moyens absolus de variation de y, tma(y), dans les intervalles (1,7), (2,5), (5,6) et (8,9) de x;
e). Les taux instantanés absolus de variation de y, tia(y), aux points x=3 et x=4
d), Calculez le taux moyen relatif de variation de y, t.m.r.(y), dans l’intervalle (8,9) par rapport à la valeur de y correspondant au point initial, au point final et au point central de cet intervalle;
g). Calculez le taux instantané relatif de variation de y, t.i.r.(y) au point central de l’intervalle (8,9)
2. Calculez le tia(y) des fonctions suivantes:
a).
b).
c).
d).
3. Calculez le tir(y) des fonctions suivantes:
a).
b).
c).
d).
avec a = constante
4. Calculez le tia du tia(y) de

5. Soit la fonction
 , vérifiez que
, vérifiez que

(cf. 2.3)
Considérez un modèle qui met en relation la caractéristique y avec le temps t, où la supposition de base est:
, pour
Adoptez la condition initiale pour
 sera y=30
sera y=30
1. Comment désignez-vous le modèle?
Écrivez l’expression générale pour la valeur de la caractéristique y à l’instant t;
2. Calculez la valeur de y quand t = 0,1,2,3,4,5,6 et dessinez le graphique de y contre t
3. Considérant l’intervalle de temps, Dt, de
 à
à

a). Calculez la variation de y pendant l’intervalle référé Dt;
b). Calculez la valeur centrale de y dans l’intervalle Dt;
c). Calculez la valeur accumulée de y dans cet intervalle, ycum;
d). Calculez la valeur moyenne,
, de y, dans l’intervalle Dt;
e). Calculez la moyenne arithmétique simple de y dans l’intervalle Dt;
f). Vérifiez que la moyenne arithmétique de y est égale à la valeur moyenne,
, et égale à la valeur centrale, ycentral, de y dans cet intervalle.
g). On prétend vérifier que dans le cas du modèle linéaire le tma(y) = tia(y) = constante. Pour cela calculez pour l’intervalle Dt cité plus haut le tma(y) et le tia(y) et comparez les résultats.
Répétez l’exercice 3 en considérant l’intervalle de t = 0 à t = 10.
(cf. 2.4)
Considérez un modèle qui met en relation la caractéristique y avec le temps t, selon la supposition de base suivante:
|
|
pour
|
Adoptez la condition initiale: pour
 on aura
on aura
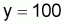
1. Écrivez l’expression générale pour la valeur de la caractéristique y à l’instant t;
a). Calculez la valeur de y aux instants t =1,2,3,4,5,6.
b). Représentez graphiquement les valeurs de y calculées ci-dessus contre les valeurs correspondantes de t.
c). Représentez graphiquement les valeurs de lny contre les valeurs données de t.
2. Considérant l’intervalle de temps Dt = (3,6)
a). Calculez la variation de y, Dy, pendant l’intervalle Dt.
b). Calculez ycentral dans l’intervalle Dt.
c). Calculez la valeur de ycum dans l’intervalle Dt.
d). Calculez
dans l’intervalle Dt.
e). Montrez que la moyenne géométrique des valeurs de y pour
y
est égale à ycentral et approximativement égale à
dans cet intervalle.
f). Montrez que dans cet intervalle
3. Considérez maintenant l’intervalle de temps de
 à
à
 . Répétez les
calculs de la question 2-alineas a), c) et d) pour cet intervalle.
. Répétez les
calculs de la question 2-alineas a), c) et d) pour cet intervalle.
(cf. 3.2)
GROUPE I
Dans le stock de cardine franche, Lepidorhombus whiffiagonis, des Divisions VIIIc et IXa du CIEM le Groupe de Travail d’Évaluation du CIEM (ICES, 1997a) a estimé que les poissons recrutent à la phase d’exploitation au début de l’âge de 1 an et qu’en 1996 le taux instantané de mortalité total pendant la phase d’exploitation a été 0.7 an-1.
Considérez une cohorte de cardine franche qui a recruté pendant la phase d’exploitation avec un effectif de 1000 individus. Considérez l’intervalle entre le début de l’âge 1 et la fin de l’âge 7 ans comme la phase d’exploitation.
1.
a). Dites quelle est la valeur du tir de la variation de
dans cet intervalle.
b). Dites quelle est la valeur du tir de la mortalité de
dans cet intervalle.
c). Calcule le taux annuel de survie pendant cet intervalle.
d). Calculez le taux annuel de mortalité pendant cet intervalle.
2.
a). Calculez le nombre de survivants au début de chaque âge de cet intervalle.
b). Calculez le nombre de survivants à la fin de l’âge de 7 ans.
c). Faites le graphique du nombre de survivants contre l’âge dans cet intervalle.
d). Calculez le nombre de morts à chaque âge de cet intervalle.
e). Dites quel est le nombre de morts pendant toute la phase d’exploitation.
f). Déterminez le pourcentage du nombre initial de l’âge de 3 ans qui survivent jusqu’au début de l’âge de 6 ans.
g). Déterminez le pourcentage du nombre initial de l’âge de 3 ans qui meurent jusqu’au début de l’âge de 6 ans.
h). Calculez le nombre moyen de survivants pendant chaque âge de l’intervalle donné.
i). Calculez le nombre accumulé de survivants aux âges de 3 à 5 ans.
j). Calculez le nombre moyen de survivants entre les débuts des âges de 3 et 6 ans.
GROUPE II
Le Groupe de Travail du CIEM où a été évalué le stock de sardine ibérique, Sardina pilchardus, a estimé les taux de mortalité pour chaque âge en 1995 (ICES, 1997b) qui sont présentés dans le tableau suivant:
|
Groupe d’âge |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Taux annuel de mortalité |
0.36 |
0.43 |
0.54 |
0.63 |
0.66 |
0.68 |
0.72 |
Supposez que ces taux correspondent à une cohorte.
1. Les taux peuvent, comme on l’a déjà vu, être de divers genres (ex: tma, tmr, tia et tir et les taux relatifs ont étés référés à diverses valeurs de caractéristiques). Quel type de taux est le taux annuel de mortalité ?
2. Calculez le taux de survie dans chaque classe d’âge.
3. Calculez le coefficient de mortalité total pour chaque classe d’âge.
4. Calculez le taux de survie entre le début de l’âge 1 et la fin de l’âge 4.
5. Calculez le taux moyen annuel de survie dans l’intervalle d’âges.
GROUPE III
Considérez une cohorte d’une certaine espèce pour laquelle le nombre de survivants au début de l’âge 2 ans est 4325, alors que le nombre de survivants à la fin de l’âge 2 ans est 2040.
1. Calculez le nombre moyen d’individus à l’âge de 2 ans et le nombre d’individus d’âge 2.5 ans. Comparez les résultats.
2. Si le taux annuel de mortalité de cette cohorte aux âges de 3 et 4 ans est de 70% et 60% respectivement, calculez le pourcentage du nombre initial d’individus à l’âge de 3 ans qui survivra jusqu’à la fin de l’âge de 4 ans.
Dites quel est le rapport entre les taux de survie pendant la période comprenant les âges 3 et 4 ans et les taux annuels de survie aux âges de 3 et 4 ans.
(cf. 3.3)
GROUPE I
Selon le Groupe de Travail d’Évaluation du CIEM
(ICES, 1996a) en 1995 les taux instantanés relatifs de mortalité
totale et naturelle à l’âge de 3 ans du stock de merlan bleu,
Micromesistius poutassou, ont été estimés comme
étant respectivement 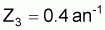 et
et 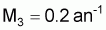 . Cette
année-là le nombre de survivants au début de
l’âge de 3 ans a été de 2600 millions
d’individus.
. Cette
année-là le nombre de survivants au début de
l’âge de 3 ans a été de 2600 millions
d’individus.
1. Calculez, pour la cohorte de 1992 et pour l’âge de 3 ans:
a). Le taux annuel de survie et le taux annuel de mortalité total.
b). Le taux instantané relatif de mortalité par pêche.
c). Le taux d’exploitation.
d). Le nombre de morts pendant l’âge.
e). Le nombre moyen de survivants pendant l’âge.
f). La capture totale en nombre d’individus de 3 ans.
g). Le nombre de survivants à la fin de l’âge.
GROUPE II
Le groupe d’âge de 4 ans du stock (Div. ICES VIIe-h) de merlan, Merlangius merlangus merlangus, est exploité simultanément par des flottilles de chalut de crustacés et chalut de fond pour poissons.
Le Groupe de Travail du CIEM qui évalue ce stock estime (ICES, 1996a) que, en 1995, le taux instantané de mortalité total de cet âge (4 ans) a été Z = 1.3 an-1. Admettez, pour cet exercice, que le taux instantané de mortalité par pêche causé par la flottille de chalut de crustacés a été Fc = 0.5 an-1, alors que la valeur correspondante pour la flottille de chalut de fond pour les poissons a été Fp = 0.6 an-1. Le Groupe a aussi considéré le taux instantané de mortalité naturel, M = 0.2 an-1.
1. En 1995 17.66 millions d’individus ont été recrutés à l’âge 4 ans.
a). Calculez le nombre total de morts à cet âge.
b). Calculez le nombre moyen de survivants à cet l’âge.
c). Calculez le taux d’exploitation de chacune des flottilles.
d). Calculez le taux d’exploitation total.
e). Calculez la capture en nombre effectuée pour chacune des flottilles et la capture totale en nombre.
f). Calculez le nombre de survivants à la fin de l’âge. (Il n’est pas obligatoire de résoudre les questions dans l’ordre présenté).
GROUPE III
Pour cet exercice admettez que le nombre moyen de survivants de la cohorte de 1990 d’un stock d’anchois européen, Engraulis encrasicholus, à l’âge de 2 ans a été calculé comme étant de 50 millions d’individus. Pendant l’année 1992, 70 millions d’individus ont été capturés, 40% d’entre eux par la flottille nationale, et l’on estime que 80 millions sont morts de causes naturelles.
1. Pour cet âge et cette cohorte:
a). Calculez le taux d'exploitation total et des flottilles nationales et étrangères.
b). Calculez les coefficients de mortalité totale, naturelle et par pêche.
c). Calculez les taux instantanés de mortalité par pêche causés par la flottille nationale et par la flottille étrangère.
d). Calculez le nombre de survivants au début et à la fin de l'âge. (Il n'est pas obligatoire de résoudre les questions dans l'ordre présenté).
GROUPE IV
Selon le Groupe de Travail d’évaluation du CIEM (ICES, 1997a) les coefficients de mortalité par pêche de la cohorte de 1976 du stock de sole, Solea vulgaris, de la Mer Celtique à chaque âge de 2 à 8 ans (tableau suivant) ont été estimés. Le coefficient de mortalité naturel pour ce stock est considéré constant et égal à 0.1 an-1. On estime qu'au début de l’âge de 6 ans il y avait 1112 millions de survivants de cette cohorte.
|
Âge |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Fi |
0.07 |
0.22 |
0.33 |
0.41 |
0.45 |
0.41 |
0.74 |
1. Calculez le nombre de survivants de cette cohorte au début de chacun des âges indiqués ci-dessus.
2. Calculez le nombre de morts pour chacun des âges indiqués dans le tableau.
3. Calculez le taux d'exploitation supporté par cette cohorte à chaque âge.
4. Calculez le nombre moyen de survivants à chacun des âges indiqués.
5. Calculez la capture en nombre extraite de cette cohorte à chaque âge indiqué ci-dessus, en utilisant deux méthodes différentes.
(cf. 3.4)
GROUPE I
Les paramètres de l'équation de croissance en longueur de von Bertalanffy pour le stock de baudroie rousse (Div. VIIIc et IXa du CIEM), Lophius budegassa, ont été estimés ainsi (Duarte et al., 1997):
Longueur asymptotique = 101.69 cm
Coefficient de croissance en longueur = 0.08 an-1
Âge théorique où la longueur est nulle = -0.2 an
1. Calculez la longueur théorique correspondante à l'âge de 3.84 an
2. Calculez la longueur au début des âges de 1 à 12 ans.
3. Calculez, pour chaque âge indiqué ci-dessus, la longueur centrale.
4. Représentez graphiquement la courbe de croissance en longueur de Bertalanffy pour ce stock.
GROUPE II
En utilisant les paramètres de croissance donnés dans le Groupe I:
1. Calculez la longueur correspondant à chaque intervalle d’âge entre 1 et 12 ans comme étant la moyenne arithmétique simple de la longueur au début et à la fin de chaque classe.
2. Calculez la longueur moyenne de chaque âge pour le même intervalle de 1 à 12 ans selon le modèle de von Bertalanffy
3. Comparez les longueurs obtenues en a) avec celles obtenues en b) et avec les valeurs centrales de chaque âge de l'intervalle calculées dans le Groupe I.
GROUPE III
Les données présentées dans le tableau suivante représentent la longueur moyenne (cm) par âge (ans) obtenue de lectures directes d’âge réalisées avec des exemplaires du stock de baudroie rousse, Lophius budegassa, (Div. VIIIc et IXa).
|
t |
Lt (cm) |
t |
Lt(cm) |
|
1 |
9.2 |
7 |
44.4 |
|
2 |
16.5 |
8 |
49.0 |
|
3 |
22.9 |
9 |
52.3 |
|
4 |
28.8 |
10 |
55.0 |
|
5 |
34.7 |
11 |
60.8 |
|
6 |
38.6 |
12 |
63.4 |
À partir de ces données les paramètres de l'équation de croissance selon le modèle de Gompertz ont été estimés ainsi:
|
Gompertz: |
Lsymbol.gif = 73.7 cm; |
k = 0.22 an-1 |
t* = - 2.76 an |
(rappelez-vous que t* est l’âge correspondant à L=1 cm)
1. Représentez graphiquement les valeurs observées.
2. Calculez pour l'intervalle 1-12 ans les valeurs de la longueur au début de chaque âge, selon le modèle de croissance de Bertalanffy et dessinez la courbe de croissance respective.
3. Calculez pour l'intervalle 1-12 ans les valeurs de la longueur au début de chaque âge, selon le modèle de croissance de Bertalanffy et dessinez la courbe de croissance respective. Déterminez le point d'inflexion de la courbe.
4. Dites quel modèle de croissance vous considérez le plus approprié pour ce cas et justifiez votre réponse.
GROUPE IV
Les données présentées dans le tableau suivant se référent au stock de baudroie rousse Lophius budegassa (Div. VIIIc et IXa).
Tableau de poids individuels par classe de longueur des échantillons de baudroie rousse Lophius budegassa recueillis par l'IEO et l'IPIMAR en 1994.
|
Li (cm) |
Wmoyeni (g) |
n |
Li (cm) |
Wmoyeni (g) |
n |
|
20- |
129 |
3 |
50- |
1685 |
28 |
|
22- |
163 |
2 |
52- |
1896 |
30 |
|
24- |
219 |
4 |
54- |
2107 |
24 |
|
26- |
265 |
14 |
56- |
2345 |
41 |
|
28- |
320 |
8 |
58- |
2569 |
41 |
|
30- |
397 |
10 |
60- |
2848 |
32 |
|
32- |
486 |
9 |
62- |
3126 |
35 |
|
34- |
545 |
57 |
64- |
3407 |
28 |
|
36- |
664 |
60 |
66- |
3700 |
19 |
|
38- |
773 |
61 |
68- |
4056 |
23 |
|
40- |
890 |
58 |
70- |
4411 |
17 |
|
42- |
1027 |
64 |
72- |
4764 |
13 |
|
44- |
1122 |
56 |
74- |
5203 |
8 |
|
46- |
1334 |
50 |
76- |
5587 |
4 |
|
48- |
1503 |
37 |
78- |
5982 |
3 |
Pour chaque classe de longueur une moyenne des poids observés est indiquée.
En se basant sur ces données, des paramètres de la relation longueur-poids ont été estimés pour ce stock ainsi:
a = 0.021
b = 2.88
1. Calculez le poids théorique pour chaque classe de longueur.
2. Marquez sur un graphique les poids observés et théoriques contre les classes de longueur.
3.Supposez que vous voulez utiliser la relation longueur-poids, avec b=3 (la constante de proportionnalité a été estimée pour cette relation comme étant a=0.013). Calculez, pour ce cas, les poids théoriques pour chaque classe de longueur. Comparez ces valeurs avec les poids théoriques estimés dans 1).
4. En utilisant les résultats obtenus jusqu'ici, écrivez l'équation de croissance de Bertalanffy, en poids, pour ce stock.
(cf. 3.6)
GROUPE I
Le recrutement à la phase d’exploitation du chinchard, Trachurus trachurus, distribué en eaux Ibéro-Atlantiques (Div. VIIIc et IXa) a lieu à l'âge de 1 an. Pour les calculs, considérez une cohorte qui a recruté sur 1000 individus pendant la phase d’exploitation, entre les âges de 1 et 10 ans.
Les paramètres de l'équation de von Bertalanffy pour cette ressource, en utilisant les longueurs moyennes à l'âge, dans la capture, du Groupe de Travail du CIEM (ICES, 1998a), ont été estimés ainsi:
Lsymbol.gif = 34.46 cm
K = 0.225 an-1
to = -1.66 an
La relation longueur-poids a aussi été estimée, en utilisant les poids moyens par âge adoptés par le GT pour les projections à Long Terme (ICES, 1998a), ainsi:
W(g) = 0.011 L(cm) 2.90
La mortalité de cette ressource est caractérisée par:
Coefficient de mortalité naturel constant au cours de la phase d’exploitation: M=0.15 an-1.
Coefficient de mortalité par pêche en 1996 (ICES, 1998a) variable selon l’âge:
|
Âge (an) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0.24 |
0.26 |
0.10 |
0.08 |
0.06 |
0.09 |
0.12 |
0.14 |
0.18 |
0.24 |
1. Organisez les calculs sur une feuille de calcul, de façon à calculer pour chaque âge de la vie de la cohorte (de l’âge 1 à 10):
a). Le nombre au début de l’âge
b). Le poids individuel au début de l’âge
c). La biomasse au début de l’âge
d). Le nombre de morts pendant l’âge
e). Le nombre moyen de survivants pendant l’âge
f). Le poids individuel moyen pendant l’âge
g). La biomasse moyenne pendant l’âge
h). La Capture en nombre pendant l’âge
i). La Capture en poids pendant l’âge
2. Déterminez:
a). Le nombre accumulé de survivants au cours de la phase d’exploitation
b). La biomasse accumulée de la cohorte tout au cours de sa vie exploitable
c). La capture totale en nombre extraite de la cohorte tout au long de sa vie exploitable
d). La capture totale en poids extraite de la cohorte tout au long de sa vie exploitable
e). Le poids moyen des individus capturés, tout au long de sa vie exploitable
f). Le poids moyen des individus de la cohorte, tout au long de sa vie exploitable
GROUPE II
Présentez les histogrammes de:
1. Nombres moyens de survivants de la cohorte à chaque âge, tout au long de sa vie exploitable
2. Biomasses moyennes de la cohorte à chaque âge, tout au long de sa vie exploitable
3. Captures en nombre par âge de la cohorte, au long de toute sa vie exploitable.
4. Captures en poids par âge de la cohorte, tout au long de sa vie exploitable.
GROUPE III
Supposez maintenant que l'on prétende analyser le cas où tous les coefficients de mortalité par pêche sont supérieurs de 30% à ceux indiqués dans le tableau du Groupe I.
1. Calculez les caractéristiques du Groupe I-2 que l'on pourrait obtenir de la même cohorte au long de sa vie, dans cette situation alternative.
2. Comparez les valeurs des caractéristiques obtenues dans ces conditions avec celles obtenues dans le Groupe I-2, en calculant le pourcentage de variation de ces caractéristiques par rapport aux valeurs respectives dans la situation précédente.
(cf. 3.7)
GROUPE I
Le recrutement à la phase exploitable du chinchard, Trachurus trachurus, distribué en eaux Ibéro-Atlantiques (Div. VIIIc et IXa) a lieu à l'âge de 1 an.
Le recrutement à la phase exploitée a été simplifié en adoptant l'âge tc=2 ans.
Les paramètres de l'équation de von Bertalanffy estimés pour cette ressource sont les suivants:
Lsymbol.gif = 34.46 cm
K = 0.225 an-1
to = -1.66
an avec la relation longueur-poids: W(g) = 0.011 L(cm) 2.90
La mortalité de cette ressource est caractérisée par:
Coefficient de mortalité naturel constant pour toute la phase exploitable M=0.15 an-1;
Coefficient de mortalité par pêche, F = 0.14 an-1, constant pour toute la phase exploitée.
1. Calculez, en utilisant la simplification de Beverton et Holt:
a). Le recrutement Rc à la phase exploitée.
b). Le nombre de morts au cours de toute la vie exploitée.
c). Le nombre accumulé de survivants au cours de toute la vie exploitée.
d). La biomasse accumulée au cours de toute la vie exploitée.
e). La capture en nombre au cours de toute la vie exploitée.
f). La capture en poids au cours de toute la vie exploitée.
g). Le poids moyen des individus de la cohorte au cours de toute la vie exploitée.
h). Le poids moyen des individus capturés au cours de toute la vie exploitée.
GROUPE II
Malgré la grande variabilité des valeurs de F des données présentées à la Section 8.8 Groupe I, on a préparé la Section 8.9 avec F constant, F = 0.14 an-1. On va maintenant comparer les résultats de la Section 8.8 avec ceux que l'on obtient dans ce group en utilisant la simplification de Beverton et Holt.
1.
a). Déterminez le nombre accumulé, la biomasse accumulée, la capture totale en nombre, la capture totale en poids et le poids moyen de la capture.
b). Comparez les résultats avec ceux obtenus à la Section 8.8 (Groupe I).
2.
a). Répétez le Groupe I de la Section 8.8 en utilisant une valeur de F 30% supérieure et calculez les pourcentages de variation du nombre accumulé, de la biomasse accumulée, de la capture totale en nombre, de la capture totale en poids et du poids moyen à la capture par rapport aux valeurs respectives obtenues dans le Groupe I.
b). Comparez les pourcentages de variation des caractéristiques obtenues à l'alinéa précédent avec celles de la Section 8.8 (Groupe III).
(cf. 4.3)
Les paramètres de mortalité et le régime d'exploitation du Stock Ibérique de merlu européen, Merluccius merluccius, des Divisions VIIIc et IXa du CIEM ont été estimés par le Groupe de Travail d’évaluation du CIEM (ICES, 1998b) ainsi:
Coefficient de Mortalité Naturel = 0.20
Niveau de Mortalité par Pêche en 1996 = 0.24
Régime d'exploitation en 1996
|
Âge |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
si |
0.00 |
0.09 |
0.29 |
1.31 |
1.25 |
1.12 |
1.32 |
1.55 |
1.55 |
Les paramètres de croissance ont été estimés ainsi:
|
Paramètres de croissance de
von |
Relation longueur-poids, |
|
Lsymbol.gif = 100 cm |
a = 0.004 |
Au début de 1996 le stock considéré avait la structure suivante en nombre par âge, représentant i l’âge et Ni le nombre de survivants au début de l’âge i, exprimé en millions d'individus:
|
âge |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Ni |
83 |
27 |
41 |
30 |
22 |
11 |
6 |
3 |
5 |
GROUPE I
1. Estimez les poids individuels au début de chaque âge, le nombre total d'individus et la biomasse totale du stock au début de l'année.
2. Estimez le poids moyen individuel, le nombre moyen de survivants, la biomasse moyenne, la capture totale en nombre, la capture totale en poids et le poids moyen à la capture et du stock, pendant l'année de 1996.
3. Supposant un recrutement en 1997 égal à 100 millions d'individus calculez pour le début de l'année de 1997:
a). La structure en nombre du stock
b). La structure en biomasse du stock
c). Le nombre total d'individus du stock
d). La biomasse totale du stock
(notez que le stock au début de 1997 est équivalent au stock à la fin de 1996, excepté le recrutement qui doit être estimé séparément).
GROUPE II
Les chercheurs ont alerté que le niveau de pêche, en 1996, était trop élevé devant être réduit, et ont suggéré une réduction dans l'ordre des 40% pour que dans le futur l'on puisse obtenir des captures en poids et des biomasses plus convenables.
Comme alternative ils ont aussi suggéré, pour améliorer l'exploitation de ce stock, l'augmentation de la taille de la maille des filets de pêche.
1. Les administrateurs des pêches ont demandé aux chercheurs qu'ils évaluent la biomasse moyenne du stock, la capture en nombre, la capture en poids et le poids moyen à la capture au cours de 1997 dans les cas:
a). De maintien du régime de pêche de 1996 (situation status quo)
b). De réduction de 40% du niveau de pêche de 1996.
2. Les administrateurs des pêches ont aussi demandé aux chercheurs qu'ils évaluent la capture en poids et la biomasse moyenne résultant du maintien, en 1997, du niveau de pêche de 1996 mais en introduisant une nouvelle taille de maille de filet de pêche. Pour cet exercice admettez que les chercheurs ont proposé le nouveau régime d'exploitation suivant:
|
âge |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
si |
0.00 |
0.00 |
0.03 |
1.50 |
1.65 |
1.75 |
1.80 |
1.80 |
1.80 |
Effectuez les calculs, présentez les résultats et commentez les changements de la capture en poids et de la biomasse moyenne par rapport à 1996.
3. Évaluez les effets sur la capture en poids et sur la biomasse moyenne résultant de l'adoption simultanée en 1997 de la réduction de 40% du niveau de pêche de 1996 et de l'introduction du nouveau régime d'exploitation (présentés aux numéros 1 et 2). Présentez les résultats et commentez-les.
(cf. 4.4)
Les paramètres de mortalité du Stock Ibérique (Div. VIIIc et IXa) de Sardine, Sardina pilchardus, ont été estimés par le Groupe de Travail d’évaluation du CIEM (ICES, 1997b) ainsi:
Coefficient de
Mortalité Naturel = 0.33

Niveau de Mortalité par
Pêche en 1996 = 0.56

Indépendamment de la durée de la phase d’exploitation de ce stock, considérez pour cet exercice que la phase d’exploitation a lieu dès le début de l’âge zéro jusqu'à la fin de l’âge six.
Régime d’exploitation, si, en 1996
|
so |
s1 |
s2 |
s3 |
s4 |
s5 |
s6 |
|
0.21 |
0.41 |
0.79 |
1.18 |
1.34 |
1.43 |
1.68 |
Les paramètres de croissance individuelle et de la relation poids-longueur de ce stock ont été estimés (Pestana, 1989) ainsi:
|
Paramètres de croissance de von Bertalanffy |
Relation
poids-longueur |
|
Lsymbol.gif = 22.3 cm |
a = 0.0044 |
GROUPE I
1. Calculez l'évolution en nombre et biomasse au début de chaque âge d'une cohorte au cours de sa vie, en supposant que les paramètres de croissance, de mortalité naturelle et par pêche sont les valeurs données.
2. Le recrutement à l'âge 0 en 1996 a été estimé à 4300 millions d'individus. Calculez le nombre accumulé, la biomasse accumulée, la capture en nombre et en poids pendant toute la vie de la cohorte.
GROUPE II
Il a été estimé qu'au début de 1996 le stock considéré avait la structure en nombre par âges suivante, représentant i l’âge et Ni le nombre de survivants au début de l’âge i, exprimé en millions d'individus:
|
i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Ni |
4300 |
279 |
591 |
233 |
561 |
384 |
180 |
On prétend évaluer le stock à Long Terme. A cet effet on considère stables tous les paramètres de mortalité et de croissance pendant les années à venir. Considérez aussi que le recrutement dans ces futures années est égal au recrutement de 1996.
1. En vous basant sur ces suppositions, calculez jusqu'à l’an 2006 et au début de chaque année et de chaque âge, le nombre de survivants du stock existant en 1996.
2. Comparez les structures du stock en 2003 et 2006.
3. Comparez l'évolution de la cohorte de 1996 avec la structure du stock au début de 2003.
(cf. 4.5)
Pendant la réunion du Groupe de Travail d’évaluation (ICES, 1998b) du stock Ibérique (Div. VIIIc et IXa) de merlu européen, Merluccius merluccius, les paramètres suivants de la population, pour la période 1982-1996 ont été estimés:
|
Année |
N (âge 0) (millions) |
Biomasse de ponte (1000 tonnes) |
|
1982 |
125 |
59.8 |
|
1983 |
107 |
61.4 |
|
1984 |
136 |
58.8 |
|
1985 |
97 |
44.1 |
|
1986 |
104 |
26.4 |
|
1987 |
97 |
24.2 |
|
1988 |
84 |
22.8 |
|
1989 |
56 |
18.9 |
|
1990 |
59 |
19.4 |
|
1991 |
69 |
20.5 |
|
1992 |
86 |
21.5 |
|
1993 |
70 |
21.0 |
|
1994 |
63 |
16.5 |
|
1995 |
32 |
15.2 |
|
1996 |
83 |
18.0 |
Le recrutement annuel à la phase d’exploitation est considéré comme étant le nombre d'individus d'âge 0.
1. Dessinez le graphique de dispersion des recrutements qui en résulte, contre la biomasse de ponte parentale.
2. Les paramètres pour la relation S-R ont été estimés en accord avec les modèles de Shepherd, Ricker, Beverton & Holt et Deriso, indiqués dans le tableau suivant, de même que le coefficient de détermination, r2 , obtenu pour chaque ajustement:
|
Paramètres |
Shepherd |
Ricker |
Beverton & Holt |
Deriso |
|
Alfa (R/g) |
3.50 |
4.43 |
4.91 |
4.40 |
|
k (1000 t) |
64.94 |
78.13 |
45.39 |
106.27 |
|
c |
3.52 |
|
|
0.896 |
|
r2 |
0.71 |
0.68 |
0.66 |
0.75 |
a). Calculez les recrutements espérés pour chaque année de la période 1982-1996 en utilisant les quatre modèles S-R.
b). Le coefficient de détermination, r2, peut être utilisé pour indiquer le bon ajustement du modèle aux données observées, selon le nombre d'observations (r2 peut être interprété comme le pourcentage de variation des points observés qui est expliqué par le modèle. Les valeurs proches de 1 indiquent un bon ajustement et les valeurs proches de zéro indiquent un mauvais ajustement). En utilisant cet indicateur commentez le bon ajustement de chaque modèle.
c). Dessinez, sur le graphique de dispersion obtenu précédemment (n° 1), les courbes S-R de chaque modèle. Commentez:
(cf. 5.2.1)
Considérez le stock de morue, Gadus morhua, de la mer d'Irlande (Div. VIIa). Les paramètres suivants de mortalité et biologiques ont été estimés par le Groupe de Travail du CIEM (ICES, 1998c):
|
Coefficient de Mortalité Naturel: |
M = 0.20 an-1 |
|
Niveau de pêche en 1996: |
F96 = 0.58 an-1 |
Poids moyen (kg) à la capture et du stock:
|
âge |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
0.001 |
0.883 |
1.778 |
3.597 |
5.695 |
7.904 |
8.502 |
9.200 |
GROUPE I
Admettez pour cet exercice, que le stock était constitué par les groupes d'âge 0 à 7 ans et qu'il était exploité selon le régime d’exploitation suivant:
Régime d’exploitation:
|
Âge |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
si |
0.80 |
0.90 |
0.96 |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
1. Calculez pour 1000 recrues la capture annuelle en poids et la biomasse moyenne annuelle, à Long Terme, correspondante au niveau de pêche de 1996.
2. Adoptant le facteur Ffactor entre 0 et 2.5 an-1 à intervalles de 0.1 an-1 dessinez la courbe de la capture annuelle en poids contre Ffactor. Sur le même graphique représentez la courbe de la biomasse moyenne contre Ffactor.
3. Calculez le point de référence biologique Fmax.
GROUPE II
1. Répondez aux questions précédentes mais en considérant le régime d’exploitation suivant:
Régime d’exploitation adopté par le Groupe de Travail:
|
Âge |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
si |
0.00 |
0.20 |
0.96 |
1.30 |
1.12 |
0.67 |
0.58 |
0.58 |
a). Comparez la valeur de Fmax de cet exercice avec celui obtenu dans celle du Groupe I.
b). Calculez le point de référence biologique Fmax sachant que le Groupe de Travail considère le groupe d’âge 7 comme un groupe d’âges accumulés (7+). Ainsi, les poids moyens à la capture et du stock présentés au début de l'exercice se maintiennent, excepté le dernier groupe d’âges qui devient le groupe d’âge 7+ avec un poids moyen égal à 10.873 kg. Le régime d'exploitation se maintient aussi avec la valeur de 0.58 pour le groupe 7+.
c). Comparez les valeurs de Fmax obtenues, considérant le groupe d’âge 7 comme le dernier âge avec la valeur de Fmax obtenue quand le dernier groupe d’âge est le groupe 7+.
(cf. 5.2.2)
Considérez le stock ibérique (Div. VIIIc e IXa) de cardine à quatre taches, Lepidorhombus boscii.
Les paramètres suivants de mortalité et biologiques ont été estimés par le Groupe de Travail du CIEM (ICES, 1998b):
|
Coefficient de Mortalité Naturel: |
M = 0.20 an-1 |
|
Mortalité par pêche en 1996: |
F96 = 0.36 an-1 |
Régime d'exploitation:
|
Âge |
1 |
2 |
3 |
4 |
5 |
6 |
7+ |
|
si |
0.06 |
0.43 |
0.89 |
1.65 |
1.66 |
1.22 |
1.22 |
Poids moyen (kg) à la capture et du stock:
|
Âge |
1 |
2 |
3 |
4 |
5 |
6 |
7+ |
|
|
0.037 |
0.067 |
0.086 |
0.109 |
0.144 |
0.188 |
0.244 |
1. Adoptant la valeur 1000 pour le recrutement à la zone de pêche, calculez la capture annuelle en poids, la biomasse moyenne annuelle, et le poids moyen annuel à la capture, à Long Terme, correspondante au niveau de mortalité par pêche de 1996.
2. Adoptant le facteur Ffactor entre 0 et 2.5 an-1 à intervalles de 0.1 an-1 dessinez la courbe de capture annuelle en poids contre Ffactor. Sur le même graphique représentez la courbe de la biomasse moyenne contre Ffactor.
3. Calculez le point de référence Biologique F0.1
4. Calculez le point de référence Biologique Fmax
5. Dans le graphique où vous avez dessinez la courbe de la capture annuelle en poids et de la biomasse moyenne contre Ffactor marquez les points de référence Biologique F0.1 e Fmax que vous avez déterminé précédemment. Commentez.
6. Calculez la biomasse moyenne, la capture en poids et le poids moyen à la capture à Long Terme pour F0.1. Comparez avec les valeurs obtenues à la question 1 pour ces caractéristiques et commentez.
(cf. 5.2.3)
Pendant la réunion du Groupe de Travail d’évaluation (ICES, 1998b) du stock Ibérique (Div. VIIIc et IXa) de merlu européen, Merluccius merluccius, les paramètres suivants de la population ont été estimés:
|
Coefficient de mortalité naturel: |
M = 0.2 an-1; |
|
Mortalité par pêche en 1996: |
F96 = 0.24 an-1 |
Poids moyen à la capture (g):
|
Âge (ans) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8+ |
|
|
4 |
37 |
106 |
205 |
358 |
517 |
706 |
935 |
1508 |
Ogive de maturation (%):
|
Âge (ans) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8+ |
|
% matures |
0 |
0 |
1 |
6 |
20 |
49 |
76 |
91 |
100 |
Le Groupe de Travail a adopté, pour les projections à LP, le régime d'exploitation moyen de la période 1994-1996, qui est ci-dessous indiquée:
|
Âge (ans) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8+ |
|
si |
0.001 |
0.11 |
0.398 |
1.3 |
1.261 |
1.019 |
1.473 |
1.874 |
1.874 |
1. Calculez la biomasse moyenne annuelle, la biomasse de ponte, la capture annuelle en poids et le poids moyen à la capture, à Long Terme.
2. Dessinez la courbe de capture annuelle en poids et de la biomasse moyenne contre F, pour des valeurs de Ffactor entre 0 et 2.5 an-1, à intervalles de 0.1 an-1. Calculez les TRP´s Fmax et F0.1.
3. Calculez le point de référence biologique Fmed sachant que le recrutement (millions d'individus à l'âge 0) et les biomasses de pontes (1000 tonnes) entre 1982 et 1996, estimées par le Groupe de Travail, sont présentées dans le tableau suivant:
|
Année |
N (âge 0) (millions) |
Biomasse de ponte (1000 tonnes) |
|
1982 |
125 |
59.8 |
|
1983 |
107 |
61.4 |
|
1984 |
136 |
58.8 |
|
1985 |
97 |
44.1 |
|
1986 |
104 |
26.4 |
|
1987 |
97 |
24.2 |
|
1988 |
84 |
22.8 |
|
1989 |
56 |
18.9 |
|
1990 |
59 |
19.4 |
|
1991 |
69 |
20.5 |
|
1992 |
86 |
21.5 |
|
1993 |
70 |
21.0 |
|
1994 |
63 |
16.5 |
|
1995 |
32 |
15.2 |
|
1996 |
83 |
18.0 |
4. Calculez la biomasse moyenne, la biomasse de ponte, la capture en poids et le poids moyen à la capture à Long Terme pour Fmed. Comparez avec les valeurs obtenues à la question 1 et commentez.
5. Adoptant la relation stock-recrutement de Ricker, estimée par le Groupe de Travail (a = 4.43 R/ kg et K = 78.13 mille t) , calculez FMSY, BMSY et Y MSY. et comparez les différents F-cible estimés.
(cf. 5.3.4 & 5.3.5)
Pendant la réunion du Groupe de Travail d’évaluation (ICES, 1998b) du stock Ibérique (Div. VIIIc et IXa) de merlu européen Merluccius merluccius ont a estimé le recrutement (millions d'individus d'âge 0) et la biomasse de ponte (1000 tonnes) pour la période 1982-1996. Les valeurs obtenues sont présentées dans le tableau suivant:
|
Année |
N (âge 0) (millions) |
Biomasse de ponte (1000 tonnes) |
|
1982 |
125 |
59.8 |
|
1983 |
107 |
61.4 |
|
1984 |
136 |
58.8 |
|
1985 |
97 |
44.1 |
|
1986 |
104 |
26.4 |
|
1987 |
97 |
24.2 |
|
1988 |
84 |
22.8 |
|
1989 |
56 |
18.9 |
|
1990 |
59 |
19.4 |
|
1991 |
69 |
20.5 |
|
1992 |
86 |
21.5 |
|
1993 |
70 |
21.0 |
|
1994 |
63 |
16.5 |
|
1995 |
32 |
15.2 |
|
1996 |
83 |
18.0 |
1. Utilisant la relation historique biomasse de ponte et recrutement résultant calculez les Points-Limites de Référence Biologique, MBAL et Bloss.
(cf. 5.3.5 & 5.3.6)
GROUPE I
Pendant la réunion du Groupe de Travail d’évaluation (ICES, 1998b) du stock Ibérique (Div. VIIIc et IXa) de merlu européen, Merluccius merluccius, on a estimé, le recrutement (millions d'individus d'âge 0) et la biomasse de ponte (1000 tonnes) pour la période 1982-1996. Les valeurs obtenues sont présentées dans le tableau suivant:
|
Année |
N (âge 0) (millions) |
Biomasse de ponte (1000 tonnes) |
|
1982 |
125 |
59.8 |
|
1983 |
107 |
61.4 |
|
1984 |
136 |
58.8 |
|
1985 |
97 |
44.1 |
|
1986 |
104 |
26.4 |
|
1987 |
97 |
24.2 |
|
1988 |
84 |
22.8 |
|
1989 |
56 |
18.9 |
|
1990 |
59 |
19.4 |
|
1991 |
69 |
20.5 |
|
1992 |
86 |
21.5 |
|
1993 |
70 |
21.0 |
|
1994 |
63 |
16.5 |
|
1995 |
32 |
15.2 |
|
1996 |
83 |
18.0 |
La relation S-R de Shepherd a été ajustée aux paires de valeurs du tableau (r2=0.71), étant les paramètres de la relation les suivants:
a (kg -1) = 3.5
k (mille t) = 64.94
c = 3.52
1. Dessinez le graphique de dispersion des recrutements résultants, contre la biomasse de ponte parentale.
2. Calculez les recrutements espérés pour chaque année de la période 1982-1996 en accord avec le modèle S-R de Shepherd et dessinez, sur le graphique de dispersion précédent, la courbe respective.
GROUPE II
1. Calculez la capture annuelle en poids et la biomasse de ponte par recrue pour le stock de merlu européen utilisant les paramètres de mortalité et biologiques estimés par le Groupe de Travail pour les projections à Long Terme (donnés à la Section 8.15), nommément:
|
Coefficient de mortalité naturel: |
M = 0.2 an-1 |
|
Mortalité par pêche en 1996: |
F96 = 0.24 an-1 |
Poids moyen à la capture (g):
|
Âge (ans) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8+ |
|
|
4 |
37 |
106 |
205 |
358 |
517 |
706 |
935 |
1508 |
Ogive de maturation (%):
|
Âge (ans) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8+ |
|
% maturesi |
0 |
0 |
1 |
6 |
20 |
49 |
76 |
91 |
100 |
Régime d'exploitation moyen de la période 1994-1996:
|
Âge (ans) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8+ |
|
si |
0.001 |
0.11 |
0.398 |
1.3 |
1.261 |
1.019 |
1.473 |
1.874 |
1.874 |
GROUPE III
1. Utilisant les résultats des Groupes I et II, calculez les Points-Limites de Référence Biologique, Floss et Fcrash.
(cf. 6.7.1)
Le tableau suivant présente la capture totale (Y, t) et la biomasse moyenne (B, t) annuelles pour la pêcherie du stock Ibérique (Div. VIIIc et IXa) de sardine, Sardina pilchardus, entre 1977 et 1996, utilisées par le Groupe de Travail du CIEM (ICES, 1998a).
|
Année |
Y (t) |
|
|
1977 |
125750 |
750289 |
|
1978 |
139990 |
759192 |
|
1979 |
153441 |
763313 |
|
1980 |
191682 |
804765 |
|
1981 |
214133 |
842091 |
|
1982 |
204504 |
802573 |
|
1983 |
181139 |
713376 |
|
1984 |
202686 |
794856 |
|
1985 |
204107 |
810539 |
|
1986 |
180606 |
679808 |
|
1987 |
168825 |
547179 |
|
1988 |
158540 |
481295 |
|
1989 |
137126 |
431719 |
|
1990 |
139157 |
368099 |
|
1991 |
127756 |
316365 |
|
1992 |
126054 |
453161 |
|
1993 |
138795 |
539096 |
|
1994 |
132800 |
416842 |
|
1995 |
121384 |
368158 |
|
1996 |
111431 |
246037 |
GROUPE I
1. Calculez Fi correspondant à chaque année i.
2. Calculez les biomasses, Bi, au début de chaque année. (Utiliser la procédure proposée par Schaefer, soit, la biomasse au début d'un an est rapprochée par la moyenne arithmétique des biomasses moyennes de l'année précédente et de l'année suivante).
3. Calculez les captures d'équilibre, YE, qui correspondrait aux valeurs de F observées.
4. Calculez les biomasses moyennes d'équilibre,
 , qui correspondraient aux
valeurs de F observées.
, qui correspondraient aux
valeurs de F observées.
5. Dessinez le graphique de
 contre
Fi.
contre
Fi.
GROUPE II
Le modèle de Schaefer a été ajusté et les paramètres suivants ont été estimés
k = 1562851 t
r = 0.426 an-1
1. Calculez les biomasses d'équilibre et les captures d'équilibre correspondantes aux niveaux de pêche observés chaque année, appliquant le modèle de Schaefer.
2. Dessinez sur le graphique de l'alinéa 5 du Groupe I précédent, les biomasses d'équilibre calculées avec le modèle de Schaefer.
3. Calculez FMSY , BMSY et YMSY
4. Calculez F0.1 , B0.1 et Y0.1.
(cf. 6.7.1 & 6.7.2)
Le tableau suivant présente les captures totales annuelles et les efforts totaux respectifs de pêche d'un stock de crevette de la Mer d'Arabie pendant la période 1969 - 1978 (Sparre et Venema, 1992).
|
Année |
Capture, Y (t) |
Effort total (1000 jours) |
|
1969 |
546.7 |
1.224 |
|
1970 |
812.4 |
2.202 |
|
1971 |
2493.3 |
6.684 |
|
1972 |
4358.6 |
12.418 |
|
1973 |
6891.5 |
16.019 |
|
1974 |
6532.0 |
21.552 |
|
1975 |
4737.1 |
24.570 |
|
1976 |
5567.4 |
29.441 |
|
1977 |
5687.7 |
28.575 |
|
1978 |
5984.0 |
30.172 |
GROUPE I
1. Faites un graphique de l'indice d'abondance annuel contre l'indice de mortalité par pêche respective.
2. Le modèle de Fox a été adapté aux données. On obtient les paramètres suivants:
a = 6.150 b = - 0.028 avec un coefficient de détermination, r2 = 0.78.
a). Calculez et dessinez les courbes des conditions d'équilibre de l'indice d'abondance et de la capture totale.
b). Déterminez les points-cible MSY et 0.1.
c). Déterminez les paramètres kq, r/q et kr.
GROUPE II
Sachant que l'ajustement du modèle de Schaefer à un même ensemble de données est à l’origine des valeurs de paramètres suivantes:
a = 444.454
b = - 8.055
(r2 = 0.77)
1. Répétez les calculs demandés dans le Groupe précédent.
(cf. 6.8)
Le tableau suivant présente les captures totales annuelles (en tonnes) et les respectives captures par unité d'effort de pêche (kg/jour de pêche de l'entreprise PESCRUL) du stock de crevette rose du large, Parapenaeus longirostris, de l'Algarve pendant la période de 1983 à 1994 (Mattos Silva, 1995).
|
An |
Y (t) |
cpue (kg/jour) |
|
1983 |
538 |
235 |
|
1984 |
638 |
131 |
|
1985 |
431 |
63 |
|
1986 |
99 |
22 |
|
1987 |
37 |
8 |
|
1988 |
62 |
21 |
|
1989 |
437 |
77 |
|
1990 |
146 |
28 |
|
1991 |
126 |
26 |
|
1992 |
53 |
25 |
|
1993 |
91 |
41 |
|
1994 |
232 |
66 |
En utilisant les paramètres suivants du modèle intégré de Fox et de Yoshimoto et Clarke (1993): k= 1580 t, q=0.39 mille jours-1 et r=0.55 an-1 résolvez les questions suivantes:
1. Projetez la cpue et la capture en poids pour l'année de 1995, supposant que l'effort de pêche se maintient égal à celui de 1994 (situation status quo).
2. Déterminez les points-cible de
référence, YMSY,
 et FMSY et les
indices
et FMSY et les
indices  et
fMSY.
et
fMSY.
3. Déterminez les points-cible de
référence, Y0.1,
 et F0.1 et les
indices
et F0.1 et les
indices  et
f0.1.
et
f0.1.
4. Déterminez les pourcentages de la capacité soutenable correspondants aux points-cible FMSY et F0.1
5. En se basant sur les résultats obtenus aux questions précédentes commentez l'état du stock et de son exploitation.
6. Supposez que l'on prétend réduire l'effort de pêche en 1995 d'environ 20% par rapport à l'effort de 1994. Projetez la capture en poids pour 1995 et présentez les variations résultantes de cette réduction de l'effort sur la capture en poids et la biomasse.
(cf. 7.2)
GROUPE I
Considérez les 10 paires suivantes de valeurs de x e y:
|
|
2 |
6 |
7 |
8 |
11 |
15 |
16 |
18 |
19 |
21 |
|
yi |
13 |
40 |
52 |
56 |
78 |
105 |
111 |
130 |
132 |
149 |
1. Estimez les constantes A et B de la droite.
2. Estimez les valeurs de Y correspondantes aux valeurs de x données.
3. Calculez le coefficient de détermination
 .
.
4. Tracez le graphique avec les valeurs observées et la droite estimée. Appréciez le bon ajustement et dites si vous considérez le modèle linéaire conforme aux données observées.
GROUPE II
Les données présentées dans le tableau suivant représentent les poids individuels par classe de longueur d'échantillons de baudroie rousse Lophius budegassa, de la côte ibérique en 1994.
|
Li (cm) |
|
Li (cm) |
|
|
20- |
129 |
50- |
1685 |
|
22- |
163 |
52- |
1896 |
|
24- |
219 |
54- |
2107 |
|
26- |
265 |
56- |
2345 |
|
28- |
320 |
58- |
2569 |
|
30- |
397 |
60- |
2848 |
|
32- |
486 |
62- |
3126 |
|
34- |
545 |
64- |
3407 |
|
36- |
664 |
66- |
3700 |
|
38- |
773 |
68- |
4056 |
|
40- |
890 |
70- |
4411 |
|
42- |
1027 |
72- |
4764 |
|
44- |
1122 |
74- |
5203 |
|
46- |
1334 |
76- |
5587 |
|
48- |
1503 |
78- |
5982 |
1. En utilisant le modèle de régression linéaire simple évaluez les paramètres de la relation poids-longueur pour ce stock en considérant que Wcentral=Wmoyen. (Notez que ln Wcentral est linéaire avec ln Lcentral).
GROUPE III
Les données présentées dans le tableau suivant représentent la longueur moyenne (cm) des exemplaires au début de l’âge (années), obtenue à partir de lectures directes d’âge réalisées avec des exemplaires du stock de baudroie rousse, Lophius budegassa, (ICES Div. VIIIc et IXa), Section 8.7
|
T |
Lt |
t |
Lt |
|
1 |
9.2 |
7 |
44.4 |
|
2 |
16.5 |
8 |
49.0 |
|
3 |
22.9 |
9 |
52.3 |
|
4 |
28.8 |
10 |
55.0 |
|
5 |
34.7 |
11 |
60.8 |
|
6 |
38.6 |
12 |
63.4 |
À partir de ces données et en utilisant le modèle de régression linéaire simple évaluez les paramètres de croissance K et Lsymbol.gif selon les expressions:
1. De Ford-Walford (1933-1946)
2. De Gulland et Holt (1959)
3. De Stamatopoulos et Caddy (1989). (Les expressions pour 1), 2) et 3), ont été étudiés dans le Chapitre sur la Croissance Individuelle).
4. Commentez les résultats obtenus dans les alinéas précédents avec les valeurs des paramètres donnés à la Section 8.7.
(cf. 7.3)
REVISION DE MATRICES
GROUPE I
Considérez les matrices A et B:
|
A = |
2301 |
B = |
1103 |
|
|
1141 |
|
- 1325 |
|
|
0422 |
|
2160 |
|
|
1033 |
|
2210 |
1. Calculez à l'aide d'une feuille de calcul: A + B, A * B, Det(A), Det(B), A-1 et B-1
2. Montrez que (A.B)-1 = B-1.A-1
3. Montrez que (A.B)T = BT.AT
GROUPE II
Soient les Matrices:
|
M(4,4)= (1/4) |
1111 |
O(4,4) = |
0000 |
I(4,4) = |
1000 |
|
|
1111 |
|
0000 |
|
0100 |
|
|
1111 |
|
0000 |
|
0010 |
|
|
1111 |
|
0000 |
|
0001 |
1. Vérifiez que la matrice nulle 0 est idempotente.
2. Vérifiez que la matrice identité I est idempotente.
3. Vérifiez que la matrice M est idempotente.
4. Quelle est la trace de M et de I.
5. Calculez la caractéristique, r , de M et de I.
6. Quelle est la valeur du déterminant de M et de I.
GROUPE III
1. Vérifiez que le produit Mx, où x est le
vecteur donné par  =
(3 4 8 1), est le vecteur de dimensions (4,1) où tous les
éléments sont égaux à la moyenne
arithmétique,
=
(3 4 8 1), est le vecteur de dimensions (4,1) où tous les
éléments sont égaux à la moyenne
arithmétique,  , des 4
éléments du vecteur x.
, des 4
éléments du vecteur x.
2. Vérifiez que (I-M)x est le vecteur écart.
3. Vérifiez que la somme des carrés de xi
, S(xi2) peut
s'écrire sous la forme matricielle:
 . x
. x
4. Vérifiez que la somme des carrés des
écarts, S(xi -
 )
) ,
peut aussi s'écrire sous la forme matricielle comme:
,
peut aussi s'écrire sous la forme matricielle comme:
 (I-M)x
(I-M)x
GROUPE IV
1. Considérez le vecteur x = |
2+ |
où | |
3 | |||
5 - |
a). Écrivez le vecteur dérivée

b). Calculez
 x
x
c). Calculez
 (
( x)
x)
d). Montrez que
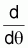 (
( x) = 2
(
x) = 2
( )
) x
x
2. Considérez le vecteur x = |
2+ 4 |
où | |
1 | |||
|
a). Écrivez la matrice dérivée
b). Calculez
x
c). Calculez la transposée de
(
x)
d). Montrez que la transposée
(
x) = 2 (
)
x
GROUPE V
Considérez le système suivant de 2 équations à 2 inconnues
|
5 = 2 A + 3 B |
4 = A - 2 B |
1. Montrez que le système d'équations peut s'écrire sous la forme matricielle:
Y(2,1) = X(2,2)  (2,1)
(2,1)
où Y est le vecteur des termes indépendants (5 et 4) du système,
le vecteur des inconnues (A et B)
et X la matrice des coefficients des inconnues
2. Vérifiez que la solution du système peut être donnée par
= (XTX)-1XTY
3. Montrez que X est une matrice carrée non singulière et que, par conséquent, la solution du système peut être
= X-1Y
ESTIMATION DES PARAMETRES DU MODELE DE YOSHIMOTO ET CLARKE (1993)
4. Estimez les paramètres k, q et r, du modèle intégré de Fox (IFOX) de Yoshimoto et Clarke (1993) en utilisant les données suivantes:
|
Année |
Y (t) |
CPUE (kg/jour) |
|
1983 |
538 |
235 |
|
1984 |
638 |
131 |
|
1985 |
431 |
63 |
|
1986 |
99 |
22 |
|
1987 |
37 |
8 |
|
1988 |
62 |
21 |
|
1989 |
437 |
77 |
|
1990 |
146 |
28 |
|
1991 |
126 |
26 |
|
1992 |
53 |
25 |
|
1993 |
91 |
41 |
|
1994 |
232 |
66 |
et qui représentent les captures totales annuelles (en tonnes) et les respectives captures par unité d'effort de pêche (kg/jour de pêche de l'entreprise PESCRUL) du stock de crevette rose du large Parapenaeus longirostris de l'Algarve pendant la période 1983 à 1994 (Mattos Silva, 1995).
Commentez les résultats obtenus avec ceux qui sont présentés à la Section 8.20.
(cf. 7.4)
Les données présentées dans le tableau suivant représentent la longueur moyenne (cm) des exemplaires au début de l’âge (ans), obtenus à partir de lectures directes d’âge réalisées avec des exemplaires du stock de baudroie rousse, Lophius budegassa, (Div. VIIIc et IXa), Section 8.7.
|
t |
Lt |
t |
Lt |
|
1 |
9.2 |
7 |
44.4 |
|
2 |
16.5 |
8 |
49.0 |
|
3 |
22.9 |
9 |
52.3 |
|
4 |
28.8 |
10 |
55.0 |
|
5 |
34.7 |
11 |
60.8 |
|
6 |
38.6 |
12 |
63.4 |
GROUPE I
1. Représentez graphiquement les valeurs de Lt contre t.
2. Estimez les paramètres de croissance K, Lsymbol.gif et t0 pour le modèle de croissance de Bertalanffy en utilisant un modèle de régression non-linéaire.
3. Estimez les valeurs de Lt correspondantes aux valeurs de t données et représentez, sur le graphique des valeurs observées, la courbe estimée. Appréciez le bon ajustement et commentez.
4. Commentez les résultats obtenus aux alinéas précédents avec les valeurs des paramètres donnés à la Section 8.7.
GROUPE II
En utilisant les données sur la biomasse de ponte et le recrutement du merlu européen présentés à la Section 8.12, évaluez les paramètres des modèles S-R de Beverton et Holt, de Ricker, de Deriso et de Shepherd.
1. Commentez les valeurs obtenues avec celles présentées à la Section 8.12.
(cf. 7.6)
GROUPE I
1. Estimez la courbe de longévité de 5% de Tanaka pour des valeurs du coefficient de mortalité naturel entre 0.0 et 5.0 an-1.
2. Calculez les valeurs de M correspondant à des longévités de 1, 2, 3, 10, 15 et 30 ans.
GROUPE II
Les paramètres de l'équation de Bertalanffy pour le stock Ibérique (Div. VIIIc et IXa du CIEM) de chinchard, Trachurus trachurus, sont les suivants:
Lsymbol.gif = 34.46 cm, LT
K = 0.225 an-1
1. Estimez la valeur de M pour cette ressource, sachant que la
température moyenne de l'eau de mer à la surface dans la zone de
cette ressource dans la Péninsule Ibérique, pour la période
1985-95, était:

GROUPE III
Considérez un certain stock halieutique pour lequel l’âge moyen de première maturation est d’environ 2.3 ans.
1. Obtenez une estimation rapprochée de M pour ce stock.
GROUPE IV
La biologie reproductive du stock de maquereau de l'Atlantique Scomber scombrus a été étudiée et l'on a estimé que l'Indice Gonadossomatique moyen des femelles matures à l'époque du frai était 0.13.
1. Estimez une valeur rapprochée pour le coefficient de mortalité naturel M de cette ressource, supposé constant pour tous les âges et toutes les années.
GROUPE V
Les chercheurs responsables de l'évaluation du stock d'une certaine ressource halieutique réalisent chaque année, en janvier, une campagne acoustique pour estimer l'abondance du stock par classes d’âge. Les statistiques de pêche leur permettent aussi d’estimer la capture par âges réalisée au cours de l'année.
Le tableau suivant présente les estimations d'abondance du stock, par classes d’âge, obtenues au cours des campagnes de 1993 et 1994, de même que la structure des captures en 1993.
|
Âge |
Nombre de survivants, N, en millions |
Capture totale en 1993(millions) |
|
|
|
Janvier 1993 |
Janvier 1994 |
|
|
2 |
243 |
353 |
11 |
|
3 |
99 |
189 |
15 |
|
4 |
86 |
67 |
20 |
|
5 |
37 |
52 |
9 |
|
6 |
13 |
22 |
3 |
|
7 |
6 |
8 |
1 |
Même en disposant de toute cette information, les chercheurs responsables de ce stock ont des difficultés dans l'application des modèles d’évaluation des ressources car ils ne disposent pas d'une estimation de M.
1. Ainsi, estimez le coefficient de mortalité naturel pour cette ressource en 1993, et aidez ce groupe de chercheurs.
GROUPE VI
Dans le tableau suivant on présente les données d'effort de pêche, en millions d'heures de chalut et le coefficient de mortalité totale Z pour une certaine pêcherie dans la période de 1987 à 1995.
|
Années |
Effort (106 heures) |
Z (an-1) |
|
1987 |
2.08 |
1.97 |
|
1988 |
2.80 |
2.05 |
|
1989 |
3.5 |
1.82 |
|
1990 |
3.6 |
2.32 |
|
1991 |
3.8 |
2.58 |
|
1992 |
- |
- |
|
1993 |
- |
- |
|
1994 |
9.94 |
3.74 |
|
1995 |
6.06 |
3.74 |
1. Déterminez M (coefficient de mortalité naturel), supposé constant pour la période 1987-1995.
2. Déterminez le coefficient de capturabilité q.
(cf. 7.7)
GROUPE I
Une campagne scientifique de zone nettoyée a permis au chercheur de l'Institut de Recherche Marines de Bergen, Norvège, d'estimer l'abondance des classes d’âge du stock de morue, Gadus morhua, en janvier 1995 (tableau suivant).
|
Âge (ans) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
N95 (109) |
1984 |
440 |
160 |
103 |
82 |
65 |
54 |
43 |
33 |
27 |
26 |
21 |
17 |
13 |
10 |
1. Représentez graphiquement les logarithmes du nombre de survivants contre l’âge.
2. Dites à partir de quel âge l'on peut considérer que le coefficient de mortalité total Z du stock est constant.
3. Estimez le coefficient de mortalité total Z du stock en janvier 1995.
GROUPE II
Le tableau suivant présente les captures moyennes, en nombre, par âge de la plie d'Europe, Pleuronectes platessa, réalisées pour chaque 100 heures de chalut de deux périodes, 1929-1938 et 1950-1958.
|
Âge (ans) |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
C/f |
1929-38 |
125 |
1355 |
2352 |
1761 |
786 |
339 |
159 |
70 |
28 |
|
C/f |
1950-58 |
98 |
959 |
1919 |
1670 |
951 |
548 |
316 |
180 |
105 |
1. Estimez le coefficient de mortalité total Z du stock dans chaque période.
2. Considérant que l'effort de pêche moyen exercé sur la limande de la mer du Nord pendant les deux périodes a été de 5 millions d'heures de chalut en 1929-1938 et de 3.1 millions d'heures de chalut en 1950-1958. Estimez dans chaque période:
a). le coefficient de mortalité naturel M;
b). le coefficient de capturabilité q;
c). et le coefficient de mortalité par pêche F.
GROUPE III
Présentez ensuite, pour une certaine ressource, la composition annuelle des captures par âge de 1988 à 1994, en millions d'individus.
CAPTURES (millions d'individus)
|
Âge |
1988 |
1989 |
1990 |
1991 |
1992 |
1993 |
1994 |
|
0 |
599 |
239 |
424 |
664 |
685 |
478 |
330 |
|
1 |
678 |
860 |
431 |
1004 |
418 |
607 |
288 |
|
2 |
1097 |
390 |
1071 |
532 |
335 |
464 |
323 |
|
3 |
275 |
298 |
159 |
269 |
203 |
211 |
243 |
|
4 |
40 |
54 |
75 |
32 |
69 |
86 |
80 |
|
5 |
6 |
9 |
13 |
18 |
8 |
25 |
31 |
|
6 |
1 |
8 |
3 |
5 |
5 |
3 |
8 |
|
7 |
6 |
0 |
1 |
0 |
1 |
1 |
1 |
1. Calculez la composition annuelle moyenne de 1988-1994.
2. Estimez Z à partir de cette composition moyenne.
3. Estimez Z à partir de l’âge moyen dans la composition moyenne de la capture.
4. Estimez Z pour chaque année de la période donnée.
5. Comparez les Zs annuels avec les Zs obtenus aux questions 2 et 3.
GROUPE IV
On présente ensuite la composition par longueur, en
équilibre, d'une certaine ressource, avec
 cm et K = 0.2
an-1.
cm et K = 0.2
an-1.
|
Classe de comp. (cm) |
35- |
40- |
45- |
50- |
55- |
60- |
65- |
70- |
75- |
80- |
85- |
90- |
95- |
|
Capture (Ci) en millions |
7 |
10 |
20 |
51 |
46 |
44 |
41 |
36 |
33 |
28 |
23 |
17 |
8 |
1. Calculez les âges relatifs correspondants à la limite inférieure de chaque classe de longueur.
2. Déterminez l'intervalle d’âge correspondant à chaque classe de longueur.
3. À partir de quelle classe peut-on considérer Z constant?
4. Déterminez Z en utilisant:
a). Les captures de chaque classe.
b). Les captures accumulées.
c). La longueur moyenne à la capture.
5. Comparez les valeurs de Z obtenues par les différentes méthodes.
GROUPE V
Pour une certaine ressource halieutique les compositions par longueur des captures sont connues pour trois périodes de temps distinctes.
|
Période |
Classes de long. (cm) |
45- |
50- |
55- |
60- |
65- |
70- |
75- |
80- |
85- |
90- |
³95 |
|
1960-69 |
Capture (Ci) en millions |
256 |
237 |
211 |
187 |
161 |
138 |
113 |
87 |
62 |
36 |
12 |
|
1970-79 |
|
268 |
226 |
180 |
141 |
105 |
76 |
50 |
30 |
15 |
6 |
1 |
|
1980-89 |
|
212 |
161 |
116 |
79 |
52 |
31 |
17 |
8 |
3 |
1 |
0 |
Considérez la classe de longueur de 45 cm comme la première classe complètement recrutée.
Adoptez K = 0.3 an-1 et
 comme les paramètres
de croissance de von Bertalanffy pour cette ressource.
comme les paramètres
de croissance de von Bertalanffy pour cette ressource.
1. Estimez les valeurs du coefficient de mortalité total Z pour chaque période et commentez les résultats.
(cf. 7.9.1)
GROUPE I
1. Considérez un intervalle de temps i,
 . Sachant que dans cet
intervalle de temps:
. Sachant que dans cet
intervalle de temps:
Mi = 0.4 an-1
Ti = 2.3 an
Ci = 230 millions d'individus
a). Adoptez la valeur 0.5 an-1 pour coefficient de mortalité par pêche pendant l'intervalle i et calculez le nombre de survivants à la fin de l'intervalle et le nombre de survivants au début de l'intervalle.
2. Considérez l'intervalle de temps i,
 . Sachant que cet intervalle
de temps:
. Sachant que cet intervalle
de temps:
Mi = 0.6 an-1
Ti = 0.9 an
Ci = 98 millions d'individus
3. Calculez la valeur du coefficient de mortalité par pêche Fi pendant l'intervalle i sachant que le nombre Ni de survivants au début de l'intervalle i est égal à 172 millions d'individus.
Considérez l'intervalle de temps (ti, t I+1). Sachant que dans cet intervalle de temps:
Mi= 0.5 an-1
Ti = 1 an
Ci = 42 millions d'individus
a). Calculez la valeur du coefficient de mortalité par pêche, pendant l'intervalle i , sachant que le nombre de survivants à la fin de l'année était Ni+1= 85 millions d'individus. Calculez la valeur de Fi en utilisant la formule de Pope.
GROUPE II
Les données du tableau suivant se réfèrent aux captures en nombre (millions) d'une cohorte de merlu européen, Merluccius merluccius, dans les eaux de la Péninsule Ibérique.
|
Âge (ans) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Ci (millions) |
712 |
3941 |
8191 |
10311 |
5515 |
4149 |
3081 |
1185 |
549 |
Adoptez une valeur de 0.2 an-1 pour le coefficient de mortalité naturel, constante pour tous les âges.
1. Supposez que la valeur du coefficient de mortalité par pêche pour le dernier âge (8 ans) a été 1.0 an-1. Calculez, par la méthode itérative et par la méthode de Pope et pour chaque âge de la cohorte:
a). La valeur du coefficient de mortalité par pêche.
b). Le nombre de survivants au début de l’âge.
c). Comparez les résultats obtenus par les deux méthodes.
d). Représentez graphiquement les valeurs de Fi estimées contre l’âge, et dites quel a été le recrutement de cette cohorte à la phase exploitée.
GROUPE III
1. Pour analyser l'influence du choix de Fterminal répétez les calculs de la question précédente, en utilisant une des méthodes précédentes, utilisant 0.3 et 1.5 an-1 comme valeur de Fterminal.
a). Représentez graphiquement les valeurs estimées de Fi et Ni contre l’âge.
b). Commentez les différences entre les graphiques pour les différentes valeurs de Fterminal.
2. Pour analyser l'influence du choix de M, répétez les calculs de la question 1 en utilisant l’une des méthodes précédentes, en utilisant des valeurs de M de 0.1 et 0.4 an-1.
a). Représentez graphiquement les valeurs estimées de Fi et Ni contre l’âge.
b). Commentez les différences entre les graphiques pour les différentes valeurs de M.
GROUPE IV
Les captures annuelles par classe d’âge d'une certaine ressource, pour les années de 1985 à 1994, sont présentées dans le tableau suivant.
|
Captures par classe d’âge (Millions d'individus) |
||||||||||
|
Ans |
||||||||||
|
Âge (années) |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
1993 |
1994 |
|
0 |
67 |
88 |
104 |
290 |
132 |
90 |
63 |
38 |
52 |
90 |
|
1 |
532 |
1908 |
1841 |
1671 |
4172 |
1915 |
1284 |
906 |
541 |
704 |
|
2 |
2070 |
1756 |
4424 |
3178 |
2534 |
6320 |
2826 |
1911 |
1322 |
741 |
|
3 |
728 |
4016 |
2256 |
4042 |
2499 |
1972 |
4742 |
2115 |
1382 |
890 |
|
4 |
353 |
945 |
3309 |
1273 |
1926 |
1170 |
883 |
2102 |
896 |
540 |
|
5 |
97 |
439 |
733 |
1730 |
558 |
827 |
479 |
356 |
807 |
316 |
|
6 |
16 |
107 |
300 |
333 |
656 |
207 |
291 |
166 |
117 |
243 |
|
7 |
25 |
8 |
73 |
136 |
126 |
243 |
73 |
101 |
54 |
35 |
|
8 |
5 |
7 |
5 |
33 |
52 |
47 |
85 |
25 |
33 |
16 |
La façon d’opérer de la flottille de pêche s’est maintenue constante pendant cette période, mais le nombre de navires a augmenté significativement. Considérez qu'actuellement la ressource est intensément exploitée.
On dispose aussi d'estimations des paramètres de croissance en poids de cette ressource et du coefficient de mortalité naturel:
|
Lsymbol.gif = 38.5 cm |
a = 0.021 de la relation W(g)-L(cm) |
|
K = 0.25 an-1 |
b = 2.784 de la relation W(g)-L(cm) |
|
to = - 0.51 an |
M = 0.3 an-1 |
1. Estimez le coefficient de mortalité par pêche et le nombre de survivants au début de l'année pour chaque classe d’âge et chaque année. Utiliser la méthode d'Analyse de Cohortes de Pope.
a). Dans le premier essai sélectionnez Fterminal = 0.5 pour le dernier âge pour tous les ans et, pour tous les âges du dernier an de la matrice.
b). Analysant la matrice F obtenue en a) sélectionnez des nouvelles valeurs de Fterminal et répétez l'application de la méthode de Pope.
2. On sait aussi que le frai a lieu dans une période limitéee, vers le début de l'année. Des campagne ont été réalisées par méthodes acoustiques, à l'époque du frai, pour estimer la biomasse de ponte (kg/heure de chalut). Les résultats obtenus sont présentés dans le tableau suivant:
|
Années |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
1993 |
1994 |
|
Indice de biomasse de ponte |
1270 |
1613 |
1629 |
1424 |
1300 |
1209 |
1000 |
718 |
476 |
326 |
L'information biologique recueillie pendant ces campagnes a aussi été utilisée pour estimer l'ogive de maturation du stock à l'époque du frai.
|
Âge (ans) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
% Matures |
0 |
1 |
20 |
50 |
80 |
100 |
100 |
100 |
100 |
a). Calculez la biomasse de ponte à l'époque du frai pour chaque année de la période 1985-1994 en utilisant les résultats de l'Analyse de Cohortes que vous avez réalisée.
b). Utilisez l'information des campagne acoustiques pour valider (ou non) l'Analyse de Cohortes.
c). Commentez la validation
(cf. 7.9.2)
GROUPE I
On présente dans le tableau suivant la composition annuelle par longueur, d'une cohorte d'une ressource avec Lsymbol.gif = 130 cm et K = 0.1 an-1.
|
Classes de longueur (cm) |
Capture, Ci (millions) |
|
6- |
1823 |
|
12- |
14463 |
|
18- |
25227 |
|
24- |
8134 |
|
30- |
3889 |
|
36- |
2959 |
|
42- |
1871 |
|
48- |
653 |
|
54- |
322 |
|
60- |
228 |
|
66- |
181 |
|
72- |
96 |
|
78- |
16 |
|
84- |
0 |
Le coefficient de mortalité naturel a été estimé comme étant M = 0.3 an-1.
1. En utilisant la méthode de Pope, et en adoptant E=0.5 comme taux d'exploitation de la dernière classe de longueur de la capture (78-), estimez le nombre de survivants au début de chaque classe de longueur, le coefficient de mortalité par pêche F et le taux d'exploitation E dans chaque classe.
2. Calculez le nombre moyen de survivants de cette cohorte.
GROUPE II
Dans les Tableaux 1 et 2 on présente l'information de base sur un stock hypothétique pendant les années de 1985 à 1994.
1. Appliquez la technique de "coupe en tranches" (slicing) à la matrice de Capture et faites des commentaires sur la validité de procéder à une analyse de cohorte par âge.
2. En utilisant cette information estimez les matrices [F] et [N] par classes de longueur et par années.
3. Calculez aussi la matrice [Fsep] et faites des commentaires sur l'hypothèse que le régime d'exploitation se maintienne constant au cours de ces années.
Tableau 1. Paramètres de croissance de la courbe de von-Bertalanffy, Lsymbol.gif et K Coefficient de Mortalité Naturelle , M et constantes a et b de la relation poids-longueur
|
Croissance |
Mortalité Naturelle |
Relation poids-longueur |
|||
|
Lsymbol.gif (cm) |
42 |
M (an-1) |
0.8 |
a |
0.0023 |
|
K (an-1) |
0.5 |
|
|
b |
3 |
Tableau 2. Matrice de capture dans mille individus, obtenus par la simulation par classes de longueur et années de la période de 1985-94
| Âges |
Classes de longueur (cm) |
Années |
|||||||||
| 1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
1993 |
1994 |
||
| 0 |
20- |
35 |
41 |
30 |
17 |
49 |
69 |
34 |
61 |
46 |
29 |
| |
21- |
338 |
400 |
292 |
167 |
472 |
662 |
327 |
593 |
442 |
276 |
| |
22- |
805 |
952 |
699 |
400 |
1127 |
1575 |
777 |
1404 |
1053 |
657 |
| |
23- |
1500 |
1766 |
1317 |
757 |
2108 |
2923 |
1436 |
2574 |
1962 |
1220 |
| |
24- |
1901 |
2222 |
1702 |
985 |
2688 |
3678 |
1795 |
3175 |
2485 |
1535 |
| |
25- |
2034 |
2357 |
1872 |
1093 |
2902 |
3900 |
1886 |
3276 |
2659 |
1627 |
| |
26- |
1898 |
2175 |
1806 |
1067 |
2739 |
3600 |
1722 |
2925 |
2482 |
1502 |
| 1 |
27- |
1951 |
1817 |
1228 |
1416 |
1445 |
2932 |
3376 |
1695 |
1785 |
2376 |
| |
28- |
1664 |
1529 |
1091 |
1276 |
1250 |
2467 |
2801 |
1369 |
1523 |
1999 |
| |
29- |
1382 |
1251 |
948 |
1125 |
1053 |
2018 |
2258 |
1071 |
1265 |
1636 |
| |
30- |
1127 |
1003 |
812 |
980 |
873 |
1619 |
1782 |
818 |
1031 |
1312 |
| |
31- |
900 |
787 |
684 |
841 |
710 |
1269 |
1372 |
607 |
823 |
1029 |
| |
32- |
694 |
595 |
560 |
702 |
558 |
959 |
1017 |
432 |
635 |
778 |
| 2 |
33- |
809 |
565 |
290 |
389 |
834 |
511 |
759 |
832 |
221 |
518 |
| |
34- |
584 |
399 |
226 |
310 |
618 |
361 |
522 |
544 |
160 |
365 |
| |
35- |
403 |
267 |
170 |
240 |
439 |
242 |
340 |
335 |
110 |
245 |
| |
36- |
262 |
168 |
122 |
178 |
294 |
152 |
207 |
191 |
72 |
154 |
| 3 |
37- |
165 |
168 |
66 |
71 |
175 |
214 |
93 |
128 |
75 |
46 |
| |
38- |
86 |
84 |
40 |
45 |
96 |
107 |
44 |
55 |
39 |
23 |
Considérez La= 20 cm et ta=0
(Extrait de: Cadima, E. & Palma, C.,1997. Cohort Analysis from annual length catch compositions. Document de Travail présenté au Groupe de Travail d’évaluation des Stocks Demersaux de la Plateforme Sud, réalisé à Copenhague, 1-10 Septembre, 1997.)
COURS D’EVALUATION DES RESSOURCES HALIEUTIQUES INSTITUTO DE INVESTIGAÇÃO DAS PESCAS E DO MAR LISBONNE, 3 NOV.-10 DEC. 1997
QUESTION 1
Considérez un certain stock avec les paramètres suivants:
|
Coefficient de Mortalité Naturel: |
M = 0.20 an-1 |
|
Mortalité par pêche en 1996: |
F96 = 1.08 an-1 |
|
Régime d'exploitation: |
|
|
Âge |
1 |
2 |
3 |
4 |
5 |
6 |
7+ |
|
sI |
0.07 |
0.23 |
0.33 |
0.49 |
0.97 |
1.00 |
1.00 |
Poids moyen (kg) à la capture et du stock:
|
Âge |
1 |
2 |
3 |
4 |
5 |
6 |
7+ |
|
|
0.053 |
0.076 |
0.111 |
0.125 |
0.158 |
0.204 |
0.337 |
Ogive de maturation (%):
|
Âge (an) |
1 |
2 |
3 |
4 |
5 |
6 |
7+ |
|
% maturesi |
34 |
90 |
100 |
100 |
100 |
100 |
100 |
Les recrutements et biomasses de ponte estimées entre 1986 et 1996 sont celles présentées dans le tableau suivant:
Tableau 1
|
Année |
N (âge 1) (mille) |
Biomasse de ponte (t) |
|
1986 |
8751 |
1957 |
|
1987 |
8305 |
1591 |
|
1988 |
7123 |
1956 |
|
1989 |
7596 |
2073 |
|
1990 |
6013 |
2287 |
|
1991 |
5054 |
1506 |
|
1992 |
9713 |
1400 |
|
1993 |
5520 |
1275 |
|
1994 |
6000 |
980 |
|
1995 |
7329 |
675 |
|
1996 |
6840 |
917 |
1. Calculez le point de Référence Biologique F0.1. Indiquez la valeur de la biomasse vierge que vous avez estimée et calculez le pourcentage B0.1/Bvierge..
2. Calculez le point de Référence Biologique Fmax.
3. Calculez le point de Référence Biologique Fmed
4. Estimez les paramètres du modèle S-R de Ricker et indiquez quelle est la valeur de la biomasse de ponte/recrue correspondant à Fcrash.
5. Commentez l'état actuel du stock et de son exploitation.
QUESTION 2
Considérez un stock dont on connaît les compositions par longueur des captures pendant 1986-1995 (Tableau 2).
De ce stock les paramètres suivants ont été estimés:
Coefficient de mortalité naturelle= 1.2 an-1
Longueur asymptotique = 39.8 cm
Coefficient de croissance = 0.8 an-1
Tableau 2 - Matrice Capture (1000 individus)
| Classes de long. (cm) |
An |
|||||||||
| 1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
|
| 14- |
10 |
9 |
8 |
9 |
7 |
18 |
13 |
12 |
15 |
8 |
| 15- |
20 |
17 |
15 |
18 |
13 |
35 |
26 |
23 |
29 |
16 |
| 16- |
29 |
25 |
23 |
26 |
19 |
52 |
39 |
34 |
42 |
24 |
| 17- |
47 |
41 |
37 |
43 |
31 |
84 |
63 |
56 |
69 |
39 |
| 18- |
92 |
80 |
72 |
83 |
60 |
164 |
122 |
108 |
134 |
76 |
| 19- |
224 |
194 |
175 |
202 |
146 |
398 |
297 |
263 |
325 |
185 |
| 20- |
261 |
226 |
203 |
234 |
169 |
461 |
343 |
305 |
376 |
214 |
| 21- |
420 |
363 |
326 |
376 |
271 |
736 |
547 |
488 |
601 |
342 |
| 22- |
335 |
525 |
603 |
506 |
511 |
365 |
983 |
571 |
657 |
741 |
| 23- |
345 |
540 |
618 |
516 |
520 |
370 |
995 |
581 |
666 |
752 |
| 24- |
422 |
661 |
751 |
622 |
625 |
444 |
1189 |
699 |
799 |
902 |
| 25- |
442 |
693 |
781 |
642 |
643 |
454 |
1212 |
718 |
818 |
923 |
| 26- |
415 |
650 |
726 |
592 |
590 |
415 |
1102 |
659 |
747 |
843 |
| 27- |
388 |
607 |
672 |
542 |
537 |
376 |
995 |
601 |
677 |
765 |
| 28- |
360 |
564 |
617 |
493 |
486 |
339 |
890 |
543 |
609 |
688 |
| 29- |
332 |
520 |
563 |
444 |
435 |
301 |
788 |
487 |
543 |
613 |
| 30- |
304 |
475 |
508 |
396 |
386 |
265 |
689 |
431 |
478 |
539 |
| 31- |
275 |
430 |
453 |
348 |
337 |
230 |
594 |
377 |
414 |
468 |
| 32- |
272 |
246 |
509 |
494 |
330 |
314 |
212 |
428 |
351 |
353 |
| 33- |
239 |
216 |
439 |
419 |
277 |
261 |
174 |
359 |
292 |
294 |
| 34- |
206 |
186 |
369 |
345 |
226 |
211 |
139 |
293 |
235 |
237 |
| 35- |
171 |
155 |
300 |
273 |
176 |
162 |
106 |
228 |
181 |
182 |
| 36- |
136 |
123 |
230 |
202 |
129 |
117 |
75 |
167 |
130 |
131 |
| 37- |
82 |
99 |
116 |
196 |
147 |
91 |
80 |
40 |
117 |
83 |
| 38- |
49 |
60 |
66 |
103 |
75 |
45 |
38 |
21 |
58 |
41 |
| 39- |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1. Estimez les valeurs du coefficient de mortalité par pêche dans chaque classe de longueur de la cohorte de 1987 (pour simplifier adoptez Fterminal = 0.5 an-1).
2. Estimez les valeurs correspondantes du nombre de survivants au début de chaque classe.
3. Dites quel est le recrutement de cette cohorte.
QUESTION 3
À un certain stock a été adapté le modèle de Production de Fox les paramètres suivants ayant été obtenus:
k = 300 000 tonnes
r = 0.50 an-1
1. Déterminez les points de référence biologique FMSY et F0.1.
2. Sachant que ces dernières années la biomasse de ce stock est autour de 30% de la biomasse vierge commentez l'état actuel du stock et de son exploitation, en vous basant sur le modèle adopté.