Michel Bertignac1
Indo-Pacific Tuna Programme
P.O. Box 2004
Colombo, Sri Lanka
1 Present address: South Pacific Commission, BP D5, Noumea, New Caledonia
ABSTRACT
A simulation model of tagging experiments of yellowfin tuna in the western Indian Ocean was developed. Discrete movements of fish occurring in a five-degree square grid are described by a diffusion parameter. Monte-Carlo data sets were created to estimate confidence limits on the parameters estimated by the model (natural mortality, catchability and diffusion rate). Several levels of number of tagged fish and location of releases were tested. The development of a scheme including two fisheries permitted the calculation of marginal interaction parameters and their precision. For that purpose, a second model dealing with the entire population of yellowfin was also developed. As expected, preliminary results indicate that the precision of the parameters is related to the recovery rate, and that it is better to tag fish in the area with high fishing mortality. Tagging about 10,000 fish should be sufficient to obtain a precision of 10% on all parameters when only one fishery is included in the model. With two fisheries, releasing fish in both fisheries seems the best alternative if good precision is expected on all parameters simultaneously. If tagged fish are released in only one fishery, the precision on the catchability of the other fishery remains low, even with a large number of fish released (up to 20,000). Tagging enough fish in the affected fishery also seems important if we want to assess with good precision the impact of one fishery on the other through marginal interaction coefficients. The impact of adding randomness to the reporting rate was also tested and showed that this parameter can have a strong impact on the precision of the catchability coefficient.
1. INTRODUCTION
The precision of the parameters estimated from a tagging experiment, e.g., natural mortality, fishing mortality and movement patterns, is closely related to the number of fish released. Thus, before designing an experiment, it is useful to know what level of tag releases is required to achieve a certain level of precision on the parameter to be estimated. One way of doing this is to conduct a series of Monte-Carlo simulations of a tagging experiment using one assumed set of parameters and different levels of tag releases. Many synthetic data sets are created using random number generation. Each of them is then used to fit the parameters. The distribution of these fitted parameters around the assumed parameters used to create the synthetic data sets gives an idea of the precision.
Hampton (1989) carried out such an analysis using two tag attrition models. The first was spatially aggregated and dealt with one fishery, whereas the second involved two fisheries with exchange of fish between them. Although this second model included movements of fish between the fisheries, it did not take account of the distribution of the tagged fish and recoveries in time and space inside each of the fisheries.
The present analysis is an adaptation of Hampton's approach. It uses a tag attrition model incorporating movement parameters. Spatial distribution of tag releases and recoveries are included in the model. Only one fishery (purse seine) is first considered. A more complicated scheme including two fisheries (purse seine + artisanal fishery) is then developed. This second scheme permits the calculation of interaction coefficients and evaluation of their precision.
The objective of this paper is to determine the optimal number of yellowfin to release in a tagging experiment that is scheduled to be conducted in the western Indian Ocean. This methodology can easily be transferred to other geographic areas.
2. THE SIMULATION MODELS
2.1 Generating Tagging Experiment Data and Fitting the Attrition Model (Model I)
The simulation starts with the generation of synthetic data sets. Probabilities associated with the fate of each tagged fish are first calculated, i.e., the probability that it be recovered in a cell (i, j) during each time interval (t, t+Dt) and be returned, the probability that it be recovered and returned without relevant information, the probability that it not be returned (due to different causes: tagged fish surviving to the end of the period, death, non-reporting). Sibert and Fournier (1994) and Kleiber and Hampton (1992) give a description of a movement model permitting the calculation of these probabilities. The number of tagged fish in each cell (i, j) at each time step is calculated using the following equation:
|
|
(1) |
To account for non-reporting, the number of tagged fish recovered is multiplied by the reporting rate of recaptured tags b. The number of tagged fish recaptured in cell (i, j) at time t and reported (Ti,j,t) is thus equal to:
Ti,j,t »b · Fi,j,t · Pi,j,t
where Fi,j,t is the fishing mortality coefficient given by:
Fi,j,t = q · Ei,j,t
If a tagging experiment with N releases is to be simulated, N pseudo-random numbers uniformly distributed on (0,1) are generated and the fates of each tagged fish n are determined using a decision-making process with assumed values for parameters (see Hampton (1989) for more details). The operation is performed several times and K data sets Dk are created. Each of the data sets is used to fit the tag attrition model and to obtain K maximum likelihood parameter estimates. These estimations are carried out using an iterative searching algorithm, the Nelder-Mead simplex algorithm (Press, et al., 1992). Average coefficients of variation can eventually be calculated (s/m × 100%).
2.2 Estimating Interaction Coefficients and Their Precision (Model II)
When two fisheries (artisanal and purse seine) are considered, the results of a tagging experiment can be used to estimate interaction coefficients. One way to do this is to apply values of parameters, estimated from the tagging experiment, to the untagged population of yellowfin. The model dealing with this population is much like the one dealing with tagged fish. A recruitment component is simply added to Model I described by Equation 1. This equation becomes:
|
|
(2) |
|
|
and |
|
To define interaction coefficients between fisheries, we used an approach similar to that of Sibert (1984). Those coefficients were calculated by measuring marginal impact of changes in the catch of the affecting fishery on the catch of the affected fishery. In our two-fisheries system, approximations of interaction can be obtained from:
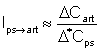 and
and
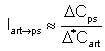
where D*Cart or D*Cps represents a small change in the catch of the affecting fishery (art for artisanal fishery and ps for purse seine fishery) and DCart or DCps its consequence at equilibrium on the affected fishery.
When simulations using Model II are carried out, small variations in the catch of the affecting fishery are obtained by altering its fishing mortality coefficients F by a given quantity (DF). F is calculated using the following equation:
F=q·E
where q and E are the catchability and fishing effort of the fishery considered. Once the system has found its new equilibrium position, interaction coefficients are calculated as follows:
where Cart(Fps + DFps, Fart) is the catch of the artisanal fishery when the fishing mortality coefficient of the purse seine fishery is increased (or decreased) by the quantity DFps and the fishing mortality coefficient of the artisanal fishery is left unchanged.
and
To estimate the distribution of the interaction coefficients, the K sets of {M, q1, q2, D} obtained from Model I are entered into Model II, K values of interaction coefficients are thus calculated. Average coefficients of variation can be estimated as described above. During that step, estimation of recruitment level is made using average values for the parameters M, q1, q2, D.
3. PARAMETERS USED TO CONDUCT THE SIMULATIONS
3.1 Study Area
The study area and fishery are designed to be as similar as possible to reality. The total study area (30°E-80°E, 25°N-35°S) is represented by a grid of 120 five-degree squares (Figure 1). It includes some land masses where the fish are not allowed to go after being released. To insert those land masses in our grid, we simplified the layout of the coast by moving them to fit the squares. Shaded areas in Figure 1 correspond to the simplified land masses. Bold lines represent boundaries where movement coefficients are set to zero. This prevents the fish from crossing them.
3.2 Fishing Effort Data
Little information is available on the spatio-temporal distribution of the artisanal fishing effort. The main fleets exploiting yellowfin are situated in the northern part of the region, from the coasts of Somalia to those of Maldives and Sri Lanka (IPTP, 1992). This fishery is mainly composed of gillnetters, except in Comoros where fishing is with pole and line. The spatial distribution of the fleets used in the simulations is presented in Figure 2. This fishing effort is set to 1 in each square where the fleets are situated and assumed to be constant throughout the year.
Monthly fishing effort distribution for the purse seiners (mainly French, Spanish, Japanese and Mauritian) is available by five-degree square for 1992. Fishing effort is expressed as total number of days spent each month in each square; 1992 was considered as typical of the present distribution of fishing effort. Figure 3 shows the distribution of effort for four months. The major part of the fleet of purse seiners is clearly moving significantly from one period to another. From December to March, vessels operate in an area east of Seychelles. They move into the Mozambique Channel in April-May. From July to November they shift to the north of Seychelles.
3.3 Natural Mortality, Tag Mortality, Tag Shedding and Non-Reporting Rate
Although an M value of 0.05 month-1 was used to conduct stock assessment of yellowfin tuna in the Indian Ocean during the last workshop held in Colombo, Sri Lanka, in 1991 (IPTP, 1992), we chose for our simulations a higher value of 0.1 month-1 for M. This value, used also in the western Pacific (J. Hampton, SPC, pers. comm.) is probably more appropriate for the size range (40-60 cm) caught during tagging experiments. Tag mortality and shedding (a) and non-reporting rates (b) ranged widely during previous tagging programmes. In this study, we took an average value of 0.9 for a and 0.6 for b. The proportion of tag recoveries reported with all relevant information was also set to 0.95.
3.4 Diffusion Coefficient
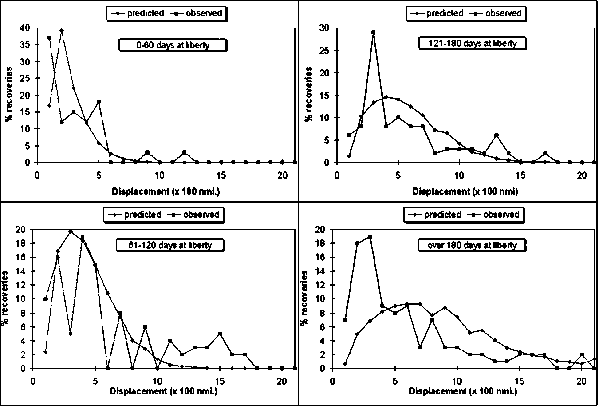
No estimations of diffusion coefficients are yet available for yellowfin in the Indian Ocean. Thus, we used our model to compile simulated recaptures by time at liberty and distance travelled and compared our predicted distributions to the actual distribution obtained after a tagging experiment conducted in the western Pacific (Hampton, pers. comm.). Using the Nelder-Mead searching algorithm again, we found the diffusion coefficient that minimised the sum of squares of differences with observations. It converged readily to a value equivalent to 0.2 cells month-1 in our grid of 300x300 nm2; thus 0.2 cells month -1 was chosen as our diffusion coefficient for the area. The predicted data match the observed data quite well (Figure 4). However, for the plot "61-120 days at liberty" and distance travelled beyond 1000 nm, the predicted recoveries are much lower than what was observed. For recoveries made after 180 days at liberty, the model predicts a larger proportion of fish recovered in remote cells than that which was observed and a smaller proportion in cells close to the cells of release. Our model assumes a uniform distribution of fishing effort over the area. This is probably not the case in reality, as fishing effort is concentrated in some areas.
Figure 4. Observed and predicted numbers of tags recovered by distance travelled from location of release (measured in a grid of 120 × 120 nm). Observed tag recoveries are from tagging experiment conducted in the western Pacific (J. Hampton, SPC, pers. comm.).
3.5 Catchability, Location and Dates of Release, and Period of Recoveries
During our simulations, several scenarios of catchability levels and locations of release were tested. Parameters corresponding to each of those scenarios are summarised in Table 1. In Simulations 1, 2 and 3, only one purse seine fishery is involved, whereas in Simulations 4, 5 and 6, an artisanal fishery was added. In the experiments with one fishery, two catchability coefficients were tested, corresponding to various levels of return rate. With releases located in high F area (group of cells where the fishing mortality coefficient is high) and a catchability of 0.0008 for the purse seine fishery (Simulation 1), the average return rate is approximately equal to 15% and corresponds to our high level assumption. A value of 0.0002 (Simulation 2) led to a return rate of 5% and corresponds to our low level hypothesis. Simulation 3 combines a low catchability level with releases made in low F area and leads to a return rate of 3%. In the simulations with two fisheries (4, 5 and 6), catchability coefficients were chosen to obtain an overall recovery rate of 10%. Fish are either tagged in one fishery (Simulation 4 and 5) or in both fishery (Simulation 6).
Table 1. Values of catchability and location of releases used in simulations.
|
Simulation |
Number of |
Purse Seine Fishery |
Artisanal Fishery |
||
|
q1 |
Location of Releases |
q2 |
Location of Releases |
||
|
1 |
1 |
0.0008 |
high F area, 5 cruises |
- |
- |
|
2 |
1 |
0.0002 |
high F area, 5 cruises |
- |
- |
|
3 |
1 |
0.0002 |
low F area, 5 cruises |
- |
- |
|
4 |
2 |
0.0004 |
high F area, 5 cruises |
0.015 |
- |
|
5 |
2 |
0.0004 |
- |
0.015 |
high F area, 5 cruises |
|
6 |
2 |
0.0004 |
high F area, 3 cruises |
0.015 |
high F area, 3 cruises |
Table 2. Location of releases in the purse seiners fishery (Simulations 1 to 4).
|
Cruise No |
High F Area |
Low F Area |
||
|
Month |
Location |
Month |
Location |
|
|
1 |
1 |
52°30'E-7°30'S |
2 |
42°30'E-17°30'S |
|
2 |
4 |
42°30'E-17°30'S |
5 |
72°30'E-2°30'S |
|
3 |
6 |
47°30'E-7°30'S |
7 |
62°30'E-17°30'S |
|
4 |
8 |
57°30'E-2°30'S |
9 |
62°30'E-17°30'S |
|
5 |
12 |
62°30'E-2°30'S |
12 |
42°30'E-17°30'S |
|
Cruise No |
Month |
Location |
|
1 |
1 |
62°30'E-22°30'N |
|
2 |
4 |
72°30'E-2°30'S |
|
3 |
6 |
72°30'E-2°30'S |
|
4 |
8 |
72°30'E-2°30'S |
|
5 |
12 |
62°30'E-22°30'N |
Table 4. Location of releases in both fisheries (Simulation 6).
|
Cruise |
Purse seine fishery |
Artisanal fishery |
||
|
Month |
Location |
Month |
Location |
|
|
1 |
1 |
52°30'E-7°30'S |
4 |
72°30'E-2°30'S |
|
2 |
4 |
42°30'E-17°30'S |
8 |
72°30'E-2°30'S |
|
3 |
6 |
47°30'E-7°30'S |
12 |
62°30'E-22°30'N |
In each simulation, 200 Monte-Carlo data sets are created. A larger number would have been preferable, but increasing the number of data sets created is very demanding on computer time, so we had to find a compromise between increasing accuracy and limiting the time that our programme was running.
CVs of the three first simulations (high and low catchability coefficient and releases made in high or low F area) are examined for each parameter to be estimated (Figure 5). Figure 5 As in the results obtained by Hampton (1989), for a given number of releases, a better precision is obtained when q is high (Simulation 1). In that case, the return rate is better (around 15%) and, consequently, more information is provided for the parameter estimation. Location of releases is also an important factor affecting the precision of estimates. At constant catchability, when fish are released in a high F area, the precision of parameters is better than when the fish are released in a low F area. The precision of the catchability coefficient seems to deteriorate more than that of the other parameters when tagging occurs in a low F area. Here also, the recovery rate is the key element. In Simulation 2, the recovery rate is equal to 5%. It drops to 2% when tagged fish are released in the low F area.
Figure 5. Coefficient of variation obtained for several levels of tagged fish released and hypotheses on catchability coefficient and location of release (see text for details on simulations). One fishery is considered. Results for each parameter are presented separately.

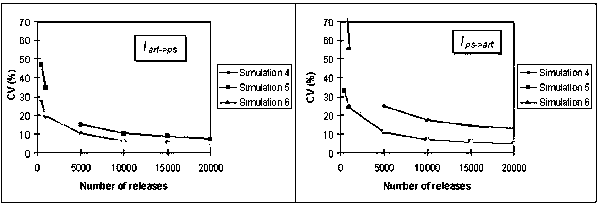
To obtain a precision of about 10% on all parameters with q set at 0.0002, it is necessary to tag around 10,000 fish if the fish are released in the high F area, whereas 15,000 to 20,000 fish have to be released if the tagging is carried out in a low F area. Adding another fishery to the system does not change the results concerning the precision on natural mortality and diffusion coefficients fundamentally (Figure 6). Reasonably good precision is still obtained with around 10,000 fish released and releasing fish in one or both fisheries does not affect the CVs. The results are quite different if our objective is to get good estimates of catchability. If fish are released in only one fishery, precision on the catchability coefficient of the other becomes low and it is thus necessary to tag more fish to get to the targeted precision (Simulations 4 and 5). When fish are released in the purse seine fishery, even with 20,000 fish released, the precision on artisanal fishery catchability remains low (CV around 20%). Releasing fish in both fisheries (Simulation 6) seems to be the best alternative if our objective is to obtain good precision for all parameters simultaneously at a given level of releases.
Figure 6. Coefficients of variation obtained for several levels of tagged fish releases and hypotheses on location of release (see text for details on simulations). Two fisheries are considered. Results for each parameter M, D, q1, q2 are presented separately.

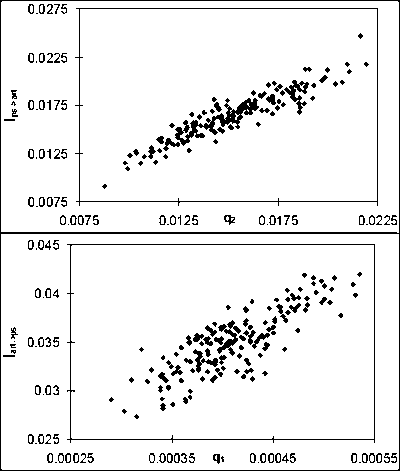
Figure 7 shows CVs on the interaction coefficients estimated using Model II with the 200 values of {M, q1, q2, D} estimated by Monte-Carlo simulation using Model I with two fisheries (Simulations 4, 5 and 6). When fish are released in one fishery, i.e., the purse seine fishery, the interaction coefficient of that fishery (affecting fishery) on the other (affected fishery), i.e., Ips®art is poorly estimated. The results are similar to those obtained above on catchability coefficients. The interaction coefficient, as we defined it, and the catchability of the affected fishery when this catchability is poorly estimated, are strongly correlated and dispersion of values around the mean are large in both cases (Figure 8). This stresses the importance of estimating with good precision the catchability of the affected fishery if the tagging experiment is to be used to estimate marginal interaction coefficients. In our two-fishery system, if we want to estimate with good precision the marginal interaction of the purse seine fishery on the artisanal fishery, it is necessary to tag enough fish in the artisanal fishery.
Up to now, several "external" parameters, such as the reporting rate b, tag shedding and mortality or fishing effort, were assumed constant during the fitting procedure. In fact, those parameters are also estimated (during previous experiments or data collection) and their estimates can be considered as a perturbation of the unknown true value of the parameter. During the fitting procedure of each simulation, instead of assuming that the parameters are constant, their values can be drawn from an appropriate distribution centred around their estimated or a priori values.
Figure 7. Coefficients of variation obtained for several levels of tagged fish release and hypotheses on location of release (see text for details on simulations), using model with two fisheries.
We tested the impact of random values of b drawn from a beta distribution with CV=0.1. This choice is arbitrary but the distribution presents the advantage of having limits of zero and one (Hampton, 1992). The results are presented in Figure 9. Adding uncertainty in the reporting rate has a strong effect on the precision of the catchability coefficient. The number of recoveries made in each cell at each time step, which influences the estimates of q, are clearly dependent on the level of b. For the other parameters, i.e., D and M, the effect of variability added to the reporting rate is less important and becomes negligible in the case of the diffusion rate. For this latter parameter, this is the distance covered by the tagged fish, which is important. The number of fish recovered per cell plays a minor role. The fact that b is assumed to be constant in time and space once it has been drawn from its distribution is also important in this respect; the relative distribution of tagged fish in space remains constant whatever values of reporting rate are chosen.
5. DISCUSSION
Results indicating that the precision of the parameters is strongly related to the recovery rate, and that it is better to tag fish in the high F areas, are not surprising and are very similar to those obtained by Hampton (1989) with his spatially-aggregated model. The incorporation of a spatial dimension and movements to the simulation model permits addressing situations where potential interactions can exist between geographically-separated fisheries. More surprisingly, tagging a sufficient number of fish in the affected fishery seems to be important if we want to assess with sufficient precision the impact of one fishery on the other through marginal interaction coefficients.
Figure 8. Estimates of interaction coefficients and catchabilities of purse seine and artisanal fishery obtained from 200 Monte-Carlo simulations with releases made in he purse seine fishery (a) or in the artisanal fishery (b). Simulations with 10,000 released yellowfin were used in both cases.
Further development of the model is required. One limitation of the analysis conducted here is the simplicity of the spatial model and its limited degree of resolution. Fish movements are described only by constant diffusion for all the area, whereas more directed movement must exist. If the fish are moving preferentially from one fishery to the other, this must have consequences on the interaction issue which we cannot assess with our current model. Adding advective movement to the model might help. It will however increase problems related to the choice of timing and direction of movement. It would be easy to adjust the model to a finer grid, e.g., 1x1 degree squares. This would, however, increase the computer time; on our 80486 (33 MHz) PC, the programme already needs up to 48 hr to estimate CVs on parameters associated with six different levels of number of tagged fish (500 to 20,000). Another limitation of the model (linked to the previous one) is the fact that the population of fish is assumed to be equally distributed in the area. A more realistic scheme would be to have fish concentrating in some areas.
Figure 9. Coefficients of variation obtained for several levels of tagged fish release. Reporting rate is either fixed or drawn from a beta distribution with CV=0.1 (see text for details on simulations).

Model II (two fisheries model) also represents an important simplification of reality. Recruitment is supposed to occur constantly over time and is uniformly distributed in space, whereas some variable pattern must exist. During the estimation of the interaction coefficients, the scaling of recruitment was done only once, using average values for the parameters {M, q1, q2, D}. A more rigorous approach would have been to estimate a recruitment level for each set of parameters.
In his analysis with two fisheries, Hampton (1989) found that with a high exchange rate between fisheries, it is necessary to tag more fish (up to 15,000 to 20,000 in each fishery) to achieve the targeted CVs of 10%. We tried some simulations with different values of diffusion, but did not observe the same results; the impact of diffusion rate was found to be low. We did not try with very high values of D; further efforts in that direction may be interesting. More generally, testing the robustness of the simulations to the violation of some of our assumptions would be necessary.
The estimated confidence intervals correspond to minimum values. The Monte-Carlo procedure used in simulations accounts for variations that can occur in the data sets due to various reasons, but depends on the assumption that the model describing the dynamics of tagged fish is appropriate. We have seen that adding randomness to the reporting rate can have a strong impact on the precision of the catchability coefficient estimated by Model I. It could, thus, be worthwhile to do the same with the fishing efforts which are also estimations and therefore have some random components.
6. REFERENCES CITED
Hampton, J. 1989. Determining optimum tag release numbers. Int. Rept. Tuna Billfish Assess. Programme, S. Pac. Comm. 12: 12 p.
Hampton, J. 1992. Assessment of skipjack and yellowfin tuna stocks in the western tropical pacific, using data from large-scale tagging experiments. Paper presented at the SPC Fifth Meeting of the Standing Committee on Tuna and Billfish, 18-19 June 1992, Honolulu, Hawaii. S. Pac. Comm. 43 p.
IPTP. 1992. Report of the Workshop on Stock Assessment of Yellowfin Tuna in the Indian Ocean. Colombo, Sri Lanka, 7-12 October 1991. Indo-Pac. Tuna Dev. Mgt. Programme. 90 p.
Kleiber, P., and J. Hampton. 1992. Progress report on the development of the Solomon Islands FAD model. Paper presented at the SPC Fifth Meeting of the Standing Committee on Tuna and Billfish, 18-19 June 1992, Honolulu, Hawaii. S. Pac. Comm. 23 p.
Press, W.H., B.P. Flannery, S.A. Teukolsky and W.T. Vetterling. 1992. Numerical Recipes in FORTRAN, Second edition. Cambridge University Press. 963 p.
Sibert, J.R. 1984. A two-fishery tag attrition model for the analysis of mortality, recruitment and fishery interaction. Tech. Rep. Tuna Billfish Asses. Programme, S. Pac. Comm. 13: 27 p.
Sibert, J., and D. Fournier. 1994. Evaluation of diffusion-advection equations for the estimation of movement patterns from tag recapture data. In: Shomura, R., J. Majkowski and S. Langi (eds.). Interactions of Pacific tuna fisheries. Proceedings of the First FAO Expert Consultation on Interactions of Pacific Tuna Fisheries, 3-11 December 1991, Noumea, New Caledonia. Vol. 1: Summary report and papers on interaction. FAO Fish. Tech. Pap. (336/1): 108-121.