B.1 Ecuaciones financieras
B.2 El significado de equivalencia
B.3 Derivación de factores de interés
B.4 Tasas de interés nominal y efectiva
B.5 Inflación e interés
B.1.1 Interés
B.1.2 El valor temporal del dinero
B.1.3 Interés simple
B.1.4 Interés compuesto
El término "interés" se utiliza para designar el costo de renta por el uso del dinero. También puede ser usado para representar el porcentaje ganado por una inversión en una operación productiva. Desde el punto de vista del prestamista, la tasa de interés es la razón entre la ganancia recibida y la inversión en un período de tiempo, que es una contribución al riesgo de pérdida, gastos administrativos y ganancia pura o beneficio. Desde el punto de vista del prestatario, la tasa de interés puede expresarse como la razón entre la cantidad pagada por el uso de los fondos y la cantidad de fondos solicitados. En este caso, el interés a ser pagado debe ser menor que la ganancia esperada.
Puesto que el dinero puede producir ganancias a una cierta tasa de interés a través de su inversión en un período de tiempo, es importante reconocer que una unidad monetaria recibida en alguna fecha futura no produce tanta ganancia como esa unidad monetaria en el presente. Esta relación entre interés y tiempo es la que conduce al concepto de "valor temporal del dinero".
Podría argüirse que el dinero también tiene un valor temporal puesto que el poder adquisitivo de una unidad monetaria varía con el tiempo. Durante los períodos de inflación, la cantidad de bienes que pueden comprarse por una determinada cantidad de dinero decrece a medida que el tiempo de compra se traslada más allá hacia el futuro. Aunque este cambio en el poder adquisitivo de la moneda es importante, todavía lo es más el que limitemos el concepto de valor temporal del dinero al hecho de que éste tiene un poder de ganancia. Cualquier referencia futura al valor temporal del dinero será restringida a este concepto. Los efectos de la inflación sobre la rentabilidad de una inversión son tratados en la sección 7.9. Es necesario el conocimiento de los distintos métodos para computar el interés, a efectos de determinar con seguridad el efecto real del valor temporal del dinero en la comparación de cursos alternativos de acción.
Normalmente, la tasa de interés de una suma de dinero se expresa como el porcentaje de la suma que es pagado por el uso del dinero en un período de un año, pero también se cotiza por períodos diferentes de tiempo. A fin de simplificar la discusión, la consideración de tasas de interés para períodos diferentes a 1 año se desarrollará al final de este Apéndice (B.4). El interés a ser abonado en el pago de un préstamo a interés simple, es proporcional a la longitud del tiempo y a la suma que ha sido prestada. Si P es la suma inicial, n el número de períodos de interés e i la tasa de interés por período, el interés simple puede ser expresado como:
I = P × n × i .......... (B.1)
Un préstamo a interés simple puede ser hecho por cualquier período de tiempo. El interés y la suma inicial se abonarán al fin del período de préstamo.
Ejemplo B.1 Interés simple
Encontrar el interés simple sobre US$ 4 500 al 8% anual para a) 1 año y b) 4 años.
Solución:
|
(a) |
I = P × n × i |
|
|
I = US$ 4 500 × 1 × 0,08 = US$ 360 |
La suma inicial más el interés, asciende a US$ 4 860 y será la deuda total al final del año.
|
(b) |
I = P × n × i |
|
|
I = US$ 4 500 × 4 × 0,08 = US$ 1 440 |
Cuando se necesita calcular el interés adeudado en una fracción del año, es común considerar al año como compuesto por 12 meses de 30 días cada uno, o sea 360 días anuales.
Ejemplo B.2 Interés simple. Período menor que un año
Encontrar el interés simple sobre US$ 1 000, para el período desde el primero de febrero al veinte de abril. La tasa de interés anual es del 8%.
Solución:
I = P × n × i
I = US$ 1 000 × (80 días/360 días) × 0,08
I = US$ 17,78
Cuando el interés ganado cada período se adiciona al monto del préstamo como se observa en la Tabla B.1 (ver Ejemplo B.3), se dice que es compuesto anualmente. La diferencia entre interés simple y compuesto se debe al efecto de la capitalización. El monto final será más elevado cuando intervienen grandes montos de dinero, tasas de interés más altas o mayor número de períodos. El interés compuesto es el que se utiliza en la práctica, motivo por el cual se empleará de ahora en adelante en lo que resta de este manual.
Tabla B.1 Cálculo de interés compuesto
|
Año |
Suma adeudada a comienzo del año (A) |
Interés adicionado a la deuda a fin de año (B) |
Suma adeudada a fin de año (A+B) |
Suma a ser pagada a fin de año |
|
1 |
1 000 |
1 000 × 0,08 = 80 |
1 080 |
0,00 |
|
2 |
1 080 |
1 080 × 0,08 = 86,4 |
1 166,4 |
0,00 |
|
3 |
1 166,4 |
1 166,4 × 0,08 = 93,3 |
1 259,7 |
0,00 |
|
4 |
1 259,7 |
1 259,7 × 0,08 = 100,8 |
1 360,5 |
1 360,5 |
El diagrama de flujo de dinero es un método gráfico que nos permite visualizar cada alternativa de inversión económica (Figura B.1). Este método gráfico provee toda la información requerida para analizar una propuesta de inversión. El diagrama de flujo de caja representa cada ingreso recibido durante el período con una flecha hacia arriba (incremento de dinero) ubicada a fin de período (se supone siempre como si ocurriese al final de dicho período). La longitud de la flecha es proporcional a la magnitud de los ingresos recibidos durante ese período. En forma similar, los egresos se representan por una flecha hacia abajo (una disminución en dinero). Estas flechas son ubicadas en una escala de tiempo que representan la duración de la alternativa.
En las Figuras B.1. (a) y (b) se observan los diagramas de flujo para el prestatario y el prestamista del ejemplo anterior, donde los gastos realizados para iniciar una alternativa se considera que tienen lugar al principio del período abarcado por la alternativa.
Figura B.1 Diagrama de flujo de caja: (a) prestatario y (b) prestamista
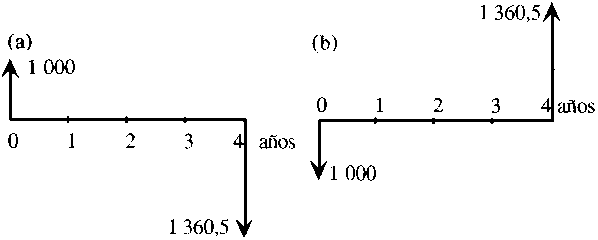
Ejemplo B.3 Interés compuesto
Encontrar el monto total de la deuda que debe pagarse al final de 4 años. La suma inicial es de US$ 1 000 al 8% anual.
Solución: Los resultados del cálculo se muestran en las Tabla B.1 y en la Figura B.1
Para evaluar alternativas de inversión, deben compararse montos monetarios que se producen en diferentes momentos, ello sólo es posible si sus características se analizan sobre una base equivalente. Dos situaciones son equivalentes cuando tienen el mismo efecto, el mismo peso o valor. Tres factores participan en la equivalencia de las alternativas de inversión:
- el monto del dinero,
- el tiempo de ocurrencia
- la tasa de interés
Los factores de interés que se desarrollarán, consideran el tiempo y la tasa de interés. Luego, ellos constituyen el camino adecuado para la transformación de alternativas en términos de una base temporal común.
B.3.1 Factor de monto compuesto con pago simple
B.3.2 Factor de valor presente con pago simple
B.3.3 Factor de monto compuesto con serie de pagos iguales
B.3.4 Factor de fondo de amortización con serie de pagos iguales
B.3.5 Factor de recuperación de capital con serie de pagos iguales
B.3.6 Serie geométrica
A continuación se derivan algunos factores de interés aplicables a situaciones comunes, tales como interés compuesto con pago simple y con serie de pagos iguales. Para su aplicación posterior en las alternativas de inversión, debemos tener en cuenta los siguientes cinco puntos:
1. El fin de un período es a su vez el comienzo del período próximo.2. P se produce al comienzo de un período, en un tiempo considerado presente.
3. F ocurre al final del enésimo período a partir de un tiempo considerado presente (siendo n el número total de períodos).
4. Definimos A como un pago simple dentro de una serie de pagos iguales realizados al final de cada período en consideración. Cuando P y A intervienen, el primer A de la serie se produce un período después de P. Cuando F y A intervienen, el último A de la serie ocurre al mismo tiempo que F. Si la serie de pagos iguales se suceden al comienzo de cada período en consideración, se denomina Ab.
5. En el planteo de las distintas alternativas, las cantidades P, F, A y Ab deben emplearse de modo tal, que reúnan las condiciones para poder conformar los modelos correspondientes a los factores usados.
En la Tabla B. 2 se muestra un resumen de las ecuaciones financieras que brindan las relaciones entre P, F y A (Jelen y Black, 1983).
Tabla B.2 Ecuaciones financieras
|
- Factor de monto compuesto con pago simple | |||
|
|
Dado P, encontrar F |
F = P × [(1 + i)n] |
F = P × FPF, i, n |
|
- Factor de valor presente con pago simple | |||
|
|
Dado F, encontrar P |
P = F × [(1 + i)-n] |
P = F × FFP, i, n |
|
- Factor de valor presente con serie de pagos iguales | |||
|
|
Dado A, Encontrar P |
|
P = A × FAP, i, n |
|
- Factor de recuperación de capital con serie de pagos iguales | |||
|
|
Dado P, encontrar A |
|
A = P × FPA, i, n |
|
- Factor de monto compuesto con serie de pagos iguales | |||
|
|
Dado A, Encontrar F |
|
F = A × FAF, i, n |
|
- Factor de Fondo de Amortización con Serie de Pagos Iguales | |||
|
|
Dado F, Encontrar A |
|
A = F × FFA, i, n |
Si una suma P se invierte a la tasa i. ¿Cuánto dinero se acumula entre capital e interés al fin del período n ?, o ¿Cuál es el valor equivalente al final del período n de la suma P invertida al iniciarse la operación?. El diagrama de flujo de dinero para esta situación financiera se muestra en la Figura B.2. Al aplicar interés compuesto a la inversión descripta en la Figura B.2., que no provee de ingresos durante los períodos intermedios, el interés ganado es como se muestra en la Tabla B.1. Allí el interés ganado se adiciona a la suma inicial al final de cada período de interés (capitalización anual). En la Tabla B.3, se muestra la deducción en términos generales.
Tabla B.3 Deducción del factor de monto compuesto con pago simple
|
Año |
Cantidad a principio de año |
Interés ganado durante el año |
Suma a ser pagada a fin de año |
|
1 |
P |
P × i |
P + P × i = P × (1+i) |
|
2 |
P × (1 + i) |
P × (1+i) × i |
P × (1+i) + P × (1+i) × i = P × (1+i)2 |
|
3 |
P × (1 + i)2 |
P × (1+i)2 × x |
P × (1+i)2 + P × (1+i)2 × i = P × (1+i)3 |
|
. |
. |
. |
. |
|
. |
. |
. |
. |
|
. |
. |
. |
. |
|
n |
P × (1 + i)n-1 |
P × (1+i)n-1 × i |
P × (1+i)n-1 + P × (1+i)n-1 × i = P × (1+i)n = F |
Figura B.2 Suma presente simple y suma futura simple
El factor resultante (1+i)n se conoce como factor de monto compuesto con pago simple y se designa como FPF; la relación es:
F = P × (1+i)n .......... (B.2)
F = P × FPF .......... (B.3)
Ejemplo B.4 Factor de monto compuesto con pago simple
Encontrar el monto compuesto de US$ 1 000 en 4 años al 8% de interés compuesto anualmente.
Solución: De la Ecuación B.3,
F = 1 000 × (1 + 0,08)4 = 1 000 × 1,3605 = US$ 1 360,5
Otro modo de interpretar la Ecuación B.3 es que, el monto F en el punto ubicado en un tiempo futuro, es equivalente al valor conocido P en el tiempo presente, para la tasa de interés dada i. La cantidad F de US$ 1 360,5 es equivalente al final de los cuatro años a la cantidad inicial P de US$ 1 000, si la tasa de interés es del 8% anual.
Despejando P de la Ecuación B.2, obtenemos:
El factor resultante (1+i)-n se conoce como factor de valor presente con pago simple y se designa FFP:
P = F × FFP ......... (B.5)
Ejemplo B.5 Factor de valor presente con pago simple
¿Cuánto debe invertirse ya (en tiempo presente) al 8% anual compuesto, de modo que puedan recibirse US$ 1 360,5 dentro de 4 años? o ¿cúal es el valor presente equivalente de US$ 1 360,5 de aquí al final de 4 años?
Solución: De la Ecuación B.5,
P = 1 360,5 × (1/1,3605) = 1 360,5 × 0,73503 = US$ 1 000
Nótese que ambos factores son recíprocos. En los métodos de valor presente y tasa interna de retorno, utilizados para evaluar la rentabilidad de proyectos (Capítulo 7), el factor de valor presente se aplica para comparar los flujos de caja con la inversión inicial.
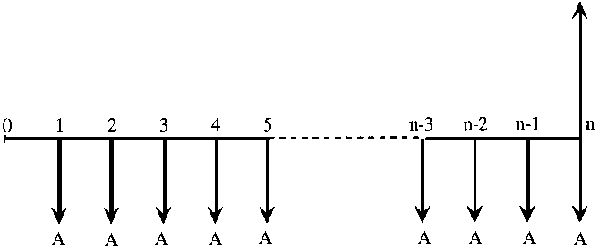
A manera de introducción, se definirá el concepto de anualidad, que consiste en una serie de pagos iguales, que se realizan a intervalos regulares de tiempo, ya sea anuales o en períodos distintos. Este esquema surge en situaciones como: acumulación de un capital determinado (recepción de cierta suma global después de un cierto número de pagos periódicos, como ocurre en algunos planes de seguros de vida), o cancelación de una deuda. La Figura B.3 es representativa del primer caso, dado que se busca el valor futuro, a partir de una serie de pagos iguales, producidos al final de sucesivos períodos de interés.
Figura B.3 Monto futuro simple con serie de pagos iguales
La suma de los montos compuestos de los diversos pagos puede calcularse por medio del uso del factor de monto compuesto con serie de pagos iguales. El modo de calcular el factor es utilizando el factor de monto compuesto con pago simple para transformar a cada A a su valor futuro:
F = A + A × (1 + i) + A × (1 + i)2 + A × (1 + i)3 + ... + A × (1+i)n-1 .......... (B.6)
Esta es una serie geométrica de razón (1+i)
F = A × [1 + (1 + i) + (1 + i)2 + (1 + i)3 + ... + (1 + i)n-1] .......... (B.7)
La suma de una serie geométrica es igual a:
En este caso:
El factor resultante [(1+i)n - 1]/i se conoce como factor de monto compuesto con serie de pagos iguales y se designa como FAF:
F = A × FAF .......... (B.11)
Ejemplo B.6 Factor de monto compuesto con serie de pagos iguales
Encontrar la cantidad compuesta por una serie de 5 pagos de US$ 500 hecha a fin de cada año al 8% anual.
Solución: El cálculo se ilustra en la Tabla B.4.
De la Ecuación B.11:
F = 500 × [(1,08)5 - 1]/0,08 = 500 × 5,8664F = US$ 2 933,2
Es decir, el monto de US$ 2 933,2 al final de los cinco períodos es equivalente a cinco pagos anuales de US$ 500, cuando la tasa de interés es del 8% por período.
Tabla B.4 Ejemplo del factor de monto compuesto con serie de pagos iguales
|
Fin de año |
Factor de monto compuesto con pagos a fin de año |
Monto compuesto al fin de 5 años |
Monto total compuesto |
|
1 |
500 × (1,08)4 |
680,2 |
|
|
2 |
500 × (1,08)3 |
629,8 |
|
|
3 |
500 × (1,08)2 |
583,2 |
|
|
4 |
500 × (1,08)1 |
540,0 |
|
|
5 |
500 |
500,0 |
2 933,2 |
Despejando A de la expresión (B.10) resulta:
El factor resultante i/[(1+i)n - 1] se conoce como factor de fondo de amortización con serie de pagos iguales.
A = F × FFA
Ejemplo B.7 Factor de fondo de amortización con serie de pagos iguales.
Si se desea acumular US$ 2 933,2 efectuando una serie de 5 pagos anuales, al 8% de interés anual, cuál es el monto requerido de cada pago?
Solución: De la Ecuación B.12 será:
La derivación de este factor y el ejemplo muestran que el factor de monto compuesto con serie de pagos iguales y el factor de fondo de amortización con serie de pagos iguales son recíprocos.
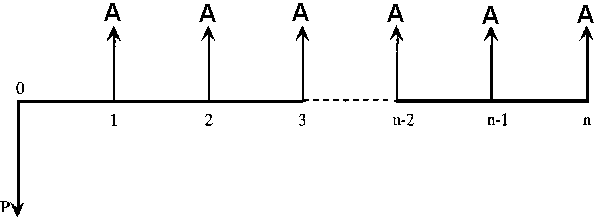
Se efectúa un depósito de monto P en un tiempo presente a una tasa anual i. El depositante desea extraer el capital más el interés ganado en una serie de montos iguales a fin de año sobre los próximos n años. Cuando se realiza la última extracción no quedan fondos en el depósito. Además, puede expresarse como cuál es el pago uniforme a final de cada período que es equivalente al monto invertido al iniciarse el primer año. El diagrama de flujo de dinero se muestra en la Figura B.4. Para determinar este factor, lo expresaremos como el producto de dos factores ya conocidos, el factor de monto compuesto con pago simple (FPFi,n) y el factor de fondo de amortización con serie de pagos iguales (FFAi,n).
A = P × FPA = P × FPF × FFA .......... (B.13)
Figura B.4 Monto presente simple y serie de pagos iguales
El factor resultante i × (1+i)n/[(1+i)n - 1] se conoce como factor de recuperación de capital con serie de pagos iguales y se designa por (FPAi,n). Se utiliza para calcular los pagos iguales requeridos para amortizar un monto presente de un préstamo, donde el interés se calcula sobre saldos. Este tipo de arreglo financiero es la base de la mayoría de los préstamos y constituye la forma más común de amortización de una deuda.
En muchos casos, los pagos anuales no se producen en una serie de pagos iguales. En algunos países es común encontrar la serie geométrica de pagos, o sea, aquélla donde cada término es igual al anterior multiplicado por un factor:
S + a × S + a 2 × S + a 3 × S +... + a n-1 × S ......... (B. 16)
donde S simboliza el primer pago y a el factor que lo multiplica. Esta serie puede simbolizar, por ejemplo, una cuota indexada mensualmente, con un interés del 5% mensual. En este caso la cuota inicial es de S. Para poder trabajar con esta serie por medio de las fórmulas conocidas, comencemos por llevar a valor presente cada una de las cuotas:
Extrayendo S/a como factor común en la serie, obtenemos:
la expresión entre paréntesis es la suma de una serie geométrica de razón a/(1+i)
Trabajando con esta expresión obtenemos:
Si en lugar de trabajar con valor presente, queremos encontrar las cuotas anuales equivalentes a la serie:
De este modo, tanto sea con P o con A podemos trabajar sencillamente con las ecuaciones conocidas.
B.4.1 Tasa compuesta discreta de interés
B.4.2 Tasa compuesta continua de interés
B.4.3 Comparación de tasas de interés
Por simplicidad, la discusión del interés ha implicado períodos de interés de un año. Sin embargo, los convenios pueden especificar que el interés sea pagado más frecuentemente, por ejemplo, cada mitad de año, cada trimestre o cada mes. Tales convenios resultan en períodos de interés de seis meses, tres meses o un doceavo de año, y la forma de componer el interés es el doble, cuatro veces o 12 veces en un año, respectivamente.
Las tasas de interés asociadas con esta forma más frecuente de componer, se cotizan normalmente sobre una base anual de acuerdo con la siguiente convención. Cuando la tasa efectiva de interés es del 4,8% compuesta cada 6 meses, el interés anual o nominal se cotiza como el "9,6% anual compuesto semianualmente". Para una tasa efectiva de interés del 2,4% compuesto a fin de cada período de 3 meses, el interés nominal se cotiza como "9,6% anual compuesto trimestralmente". Luego, la tasa nominal de interés se expresa sobre una base anual y está determinada multiplicando la tasa de interés real o efectiva por el número de períodos de interés por año.
El efecto de componer más frecuentemente es que la tasa efectiva de interés es mayor que la tasa nominal de interés. Por ejemplo, considérese una tasa de interés nominal del 9,6% compuesto semianualmente. El valor de un dólar al fin de un año cuando un dólar se compone al 4,8% por cada período de 6 meses es:
F = US$ 1 × (1,048) × (1,048) = US$ 1 × (1.048)2 = US$ 1,0983
El interés efectivo ganado sobre el dólar por un año es igual a US$ 0,0983. En consecuencia, la tasa efectiva de interés es de 9,83%. Una expresión para la tasa efectiva anual de interés puede derivarse a partir del razonamiento anterior. Sea:
i = tasa nominal de interés (anual).
ief = tasa efectiva de interés (por período).
c = número de períodos de interés por año.ief = tasa efectiva anual de interés = (1 + i/c)c - 1 .......... (B.22)
Ejemplo B.8 Tasa efectiva de interés
Calcular el valor de US$ 1 000 durante 4 años a una tasa nominal de interés del 10% compuesta cuatrimestralmente.
Solución: De la Ecuación B.22,
ief = (1+0,10/3)3 - 1ief = 10,33%
Utilizando la Ecuación B.3
F = P × FPF10,33%, 4años = 1 000 × (1 + 0,1033)
F = US$ 1 482
En el límite, el interés puede considerarse compuesto por un infinito número de veces por año o sea continuamente. Bajo estas condiciones, la tasa continua anual efectiva para el interés compuesto continuo está definido como:
Reacomodando el lado derecho de la igualdad de manera tal de incluir i en el exponente:
(1+i/c)c = (1+i/c)i × c/i .......... (B.24)
El valor del símbolo matemático e es el valor de (1 + 1/n)n como n tiende a infinito, entonces:
Por substitución,
En consecuencia, cuando el interés es compuesto continuamente,
ief = tasa anual continua efectiva de interés = ei - 1 .......... (B.27)
Las tasas de interés efectivas que corresponden a una tasa nominal del 9,6% compuesto anualmente, semianualmente, trimestralmente, mensualmente, semanalmente, diariamente y continuamente, se muestran en la Tabla B.5.
Tabla B.5 Comparación de tasas de interés
|
Frecuencia de composición |
Número de periodos por año (c) |
Tasa efectiva de interés por período (iP) |
Tasa efectivo anual de interés (ief) |
|
Anualmente |
1 |
9,6% |
9,60% (*) |
|
Semianualmente |
2 |
4,8% |
9,83% |
|
Trimestralmente |
4 |
2,4% |
9,95% |
|
Mensualmente |
12 |
0,8% |
10,03% |
|
Semanalmente |
52 |
0,1846% |
10,06% |
|
Diariamente |
365 |
0,0263% |
10,074% |
|
Continuamente |
c® ¥ |
ip® 0% |
10,076% |
Nota:
* La tasa efectiva anual de interés siempre iguala a la tasa nominal cuando el interés es compuesto anualmente.
Puesto que la tasa efectiva de interés representa el interés real ganado es esta tasa la que deberá usarse para comparar los beneficios de varias tasas nominales de interés.
Una mirada hacia el comportamiento de la economía mundial en el pasado, revela una tendencia general inflacionaria en el costo de los bienes. Durante períodos particulares esta tendencia ha sido revertida, pero en forma global parece existir una incesante presión ascendente sobre los precios. Para pequeñas tasas de inflación, este efecto en el cambio de los precios parece tener un pequeño impacto, pero cuando la inflación excede el 10% anual, puede producir consecuencias extremadamente serias, tanto para los individuos como para las instituciones (ver sección 7.9).
La inflación normalmente se describe en términos de un porcentaje anual o mensual que representa la tasa a la que los bienes del año o mes que se considera, respectivamente, se han incrementado respecto a los precios del año anterior o el mes anterior. Puesto que la tasa se define de esta manera, la inflación tiene un efecto compuesto. Luego, los precios que se inflacionan a una tasa del 8% mensual, se incrementarán el 8% el primer mes y para el siguiente mes el incremento esperado será el 8% de estos nuevos precios. Puesto que los nuevos precios incluyen el incremento original del 8%, la tasa de incremento se aplica al 8% de incremento ya experimentado.
Lo mismo es aplicable para los meses sucesivos y en consecuencia las tasas de inflación son compuestas de la misma manera que se compone una tasa de interés. Para incorporar los efectos de la inflación en estudios económicos, es necesario usar los factores de interés de tal forma que los efectos inflacionarios puedan ser reconocidos en pesos considerados en diferentes puntos en el tiempo. El procedimiento usual para evitar la pérdida en el poder adquisitivo que acompaña la inflación es seguir estos pasos:
1. Estudiar todos los costos asociados con un proyecto en términos de pesos presentes.2. Modificar los costos estimados en el paso 1, de modo que en cada fecha futura representen el costo en la misma, en términos de pesos que deben ser gastados en ese momento.
3. Calcular la cantidad equivalente de flujo de caja que resulta del paso 2 considerando el valor temporal del dinero (tasa de interés del mercado).
Es importante observar que la tasa de interés a la que se puede invertir en una operación financiera o bancaria representa la tasa de interés del mercado (estándar financiero). Esta tasa de interés está compuesta por la tasa de inflación y la oportunidad de ganar. Si estos dos efectos se separan, ir, la tasa que representa el poder de ganancia de la moneda sin inflación está relacionada con i, la tasa del mercado y con b, la tasa de inflación, por la Ecuación 7.25 de este manual:
(1 + i) = (1 + b) × (1 + iR)
Ejemplo B.9 Tasa real de interés
Una persona invierte su dinero en un banco a una tasa anual de interés del 25% y la tasa anual de inflación es del 20% ¿Cual es la tasa verdadera o real de interés?
Solución: De la Ecuación B.28,
1 + iR = (1 + 0,25)/(1 + 0,20) = 1,042iR = 4,2%
Este ejemplo muestra que el efecto de la inflación es hacer que un negocio parezca más rentable de lo que es.