por
Angel Guerra
Instituto de Investigaciones Pesqueras
Muelle de Bouzas, Vigo, España
INTRODUCCION
La embriogénesis de los cefalópodos es de un tipo especial dentro de los moluscos, caracterizándose por la segmentación incompleta de huevos telolecíticos que forman un blastodisco, pudiendo considerarse que su desarrollo embrionario es prácticamente directo, mientras que en el resto de los moluscos los heuvos presentan una segmentación espiral, que da lugar a estados larvarios del tipo trocofora o veliger, que no existen en los cefalópodos.
Las "larvas" de Octopus vulgaris aunque este término no se aplica con propiedad a los cefalópodos (Boletzky, 1974), son pelágicas. Según Rees (1950) dichas larvas alcanzan los caracteres del adulto, proporción entre la cabeza y el manto, diferenciación del tamaño de los brazos, desarrollo de la membrana interbraquial, disposición de las ventosas, etc., entre los 7 y 8 ran de longitud total.
Considerando el estado XX del desarrollo definido por Naef (1928, cit. Mangold y Boletzky, 1973) como el estado normal de un individuo recién eclosionado, Mangold y Boletzky (1973) llegan a la conclusión de que el período embrionario tiene una duración que oscila entre 25 y 125 días según la temperatura del agua: los huevos expuestos a 13°C, temperatura media del agua en la plataforma continental del Mediterráneo durante el mes de marzo, tardan 123 días en desarrollarse, a 15°C (abril) unos 80 días, de 30 a 40 días a 20°C, y entre 20 y 25 días a temperaturas de 25°C. Itami et al. (1963) señalan que la duración del desarrollo embrionario de esta especie es de unos 43 días a una temperatura que oscile entre 15 y 20°C. Por consiguiente, las puestas que se realizan entre marzo y agosto en aguas someras dan lugar a una eclosión masiva de larvas en verano, cuando el alimento - especialmente larvas de crustáceos - es particularmente abundante. No obstante, si la puesta se realiza a mayor profundidad la eclosión de los huevos puede retrasarse hasta el otoño y el invierno, debido a la baja temperatura del agua, como han observado Mangold y Boletzky (op. cit.) en las costas del Mediterráneo Catalán.
Desde la perspectiva del desarrollo embrionario se puede afirmar, por lo tanto, que en una población de pulpos existe una constante aportación de nuevos individuos (Wodinsky, 1972). No obstante, las observaciones realizadas sobre la época de freza de esta especie (Mangold, 1963; Guerra, 1975) indican la existencia de un período en el cual la aportación de nuevo individuos a la población es masiva, lo que permitiría distinguir en las distribuciones de frecuencia de tallas mensuales de la población modas asimilables a distintos grupos de edad. La existencia y persistencia en el tiempo de grupos de Octopus vulgaris pertenecientes a la misma cohorte ha sido puesta de manifiesto por Ikeda y Hatanaka (1971) y Wodinsky (1972), entre otros autores.
La fijación de las larvas al fondo acontece a los 30 ó 40 días después de la eclosión de los huevos, a una temperatura media del agua de 24,7°C, pesando entonces los animales entre 0,1 y 0,25 g (Itami et al., op. cit.).
El crecimiento durante las primeras etapas bentónicas es rápido. Itami et al. (op. cit.) concluyen que hacia los tres meses de la eclosión los pulpos alcanzan pesos comprendidos entre 11 y 69 g, con un promedio de 39 g. Las larvas observadas por estos autores en el laboratorio, después de su fijación al fondo, alcanzaron 50 mm de longitud dorsal del manto a los 90 días, y a los cinco o seis meses de su eclosión los pulpos tenían tallas de 5 y 6 cm; conclusiones similares a las que llegan Mangold y Boletzky (op. cit.) en sus experiencias de cultivo en el laboratorio.
Diferentes aspectos del crecimiento y del desarrollo de esta especie en etapas más avanzadas del desarrollo han sido objeto de varios trabajos, entre los que cabe destacar, además de los ya mencionados, los de Tanaka (1958), Nixon (l969, 1971) y Wodinsky (1972). Las conclusiones de estos estudios indican que el crecimiento de los cefalópodos es muy rápido, que después de la fijación al fondo estos animales apenas experimentan modificaciones morfológicas, y que maduran con rapidez.
Por otra parte, se ha observado (Mangold y Boletzky, op. cit.) que los individuos pertenecientes a una misma cohorte pueden presentar una variabilidad considerable de tamaño al finalizar el primer ano de vida, lo que se debe a diferentes causas, destacando entre ellas: la diferente duración del desarrollo embrionario, las características genéticas propias de cada animal, y la influencia de las condiciones ambientales que afectan profundamente a la tasa de crecimiento. Por esta razón, Mangold y Boletzky (op. cit.) consideran que no existe una estrecha relación entre el tamaño de un pulpo y su edad, lo que imposibilita el establecimiento de auténticas clases de edad en una población de pulpos.
Además de la dificultad anteriormente apuntada, hay que añadir que la determinación de la edad de los pulpos y, en general, de la mayor parte de los cefalópodos es difícil. La utilización de las bandas de crecimiento que se aprecian en las mandíbulas de los cefalópodos sin concha interna no ha proporcionado, hasta ahora, resultados satisfactorios (Clarke, 1965; Guerra, en preparación), y el empleo de otras estructuras, tales como los estatolitos, (Lipinsky, 1977) es todavía problemático.
No obstante las dificultades presentadas, nuestra hipótesis es que a partir de muéstreos amplios, periódicos y adecuados de las poblaciones de cefalópodos es posible la diferenciación de auténticas clases de tallas - asimilables a clases de edad - que permitan el estudio de su crecimiento. Este es el objetivo del presente trabajo en el que se estudia el crecimiento de Octopus vulgaris en la plataforma Noroccidental Africana a partir de las distribuciones de frecuencias de tallas obtenidas por Guerra (1978 c).
RESULTADOS
Relación talla-peso
En el cuadro 1 se expone la correspondencia entre la talla y el peso de Octopus vulgaris del Atlántico Centro-oriental. Los pesos que se indican corresponden al valor promedio de los ejemplares de cada talla examinados.
Las ecuaciones exponenciales obtenidas son las siguientes:
|
Machos |
PT = 0,937 L2,699 |
|
Hembras |
PT - 1,110 L2,594 |
|
Total |
PT = 0,976 L2,691 |
En la figura 1 se representa el crecimiento en peso en relación con la talla de Octopus vulgaris del Mediterráneo Catalan y del Atlántico Centro-oriental.
Edad correspondiente a cada talla
En el estudio del crecimiento de peces se han empleado tradicionalmente dos métodos. El primero se conoce como el método de Petersen, que consiste en el estudio del crecimiento y de la composición por edades de una población a partir de la composición de tallas de la misma; método que se basa en que en cada momento la distribución de frecuencias de tallas de una población presenta una serie de valores modales, que se pueden indentificar con los grupos de edad. El segundo método consiste en un examen individual y directo de la composición de edades de cada muestra, determinada a partir del estudio de ciertas estructuras óseas (otolitos, vértebras, etc.) o escamas de los peces, en los que quedan impresionados los ritmos de crecimiento del animal.
Como en Octopus vulgaris no existen estructuras óseas, y la utilización de las mandíbulas y de los estatolitos para determinar la posible edad de un animal no han proporcionado todavía resultados fiables, únicamente se puede utilizar en el estudio del crecimiento el método de Petersen.
Para el análisis de las distribuciones de frecuencias de tallas se han empleado des métodos, el de Harding (1949) y Cassie (1954) basado en el papel de probabilidades, y el de Battacharya (1967) denominado método de las diferencias logarítmicas. Ambos métodos permiten separar subpoblaciones gausianas de una mezcla de ellas.
Un procedimiento muy extendido en este tipo de análisis es el de agrupar las muestras de frecuencias de tallas con objeto de obtener el mayor número de individuos posibles por talla, y suavizar de este modo las irregularidades que suelen aparecer en las distribuciones de frecuencia de tallas de las muestras individuales. Buchanan-Wollaston y Hodgson (1929) discutieron los inconvenientes de este tipo de agrupamientos, señalando que muchas veces las pequeñas modas que aparecen en las distribuciones, aunque provengan de un número pequeño de individuos, puede tener significado biológico, sobre todo si las modas tienden a progresar en el tiempo. Por esta razón, se ha procedido en el caso que nos ocupa a trabajar con distribuciones de frecuencias de tallas mensuales, analizando cada distribución mediante el método del papel de probabilidades y el de las diferencias logarítmicas, comparando posteriormente los resultados obtenidos en ambos.
Los resultados obtenidos se exponen en el cuadro 2.
De esta forma se han calculado una serie de valores que suponemos representan las tallas medias de cada grupo de edad determinado. Según el criterio de Buchanan-Wollaston y Hodgson (op. cit.) para que estos valores tengan un significado válido se ha de poder seguir su desplazamiento en el tiempo, y la unión de dichos valores en el tiempo ha de poder efectuarse de la manera más natural posible. Con el fin de comprobar la secuencia de dichos valores en Octopus vulgaris se ha confeccionado la gráfica de la figura 2 en la que se aprecia la existencia de distintas progresiones de las tallas medias a lo largo del tiempo.
Para la interpretación de las líneas A, B, C, D y E que se obtuvieron, se han tenido en cuenta los siguientes criterios:
(a) que la época de freza de esta especie discurre desde marzo hasta octubre principalmente (Mangold, 1963î Mangold y Boletzky, 1973; Guerra, 1975)De acuerdo con lo expuesto anteriormente se puede calcular la edad correspondiente a cada talla media hallada. Los resultados se exponen en el cuadro 3.(b) que el crecimiento en las primeras etapas bentónicas es rápido, pudiéndose alcanzar en 90 días tallas de 4 a 6 cm (Itami et al., 1963).
Expresiones matemáticas del crecimiento
Se han empleado las expresiones de crecimiento de Von Bertalanffy (1938). Para el cálculo de los parámetros de estas ecuaciones se ha utilizado el método de Beverton (1957) (cit. Ricker, 1975).
Los ecuaciones de crecimiento en longitud más apropiadas para Octopus vulgaris del Atlántico Centro-oriental sonlas siguientes:
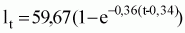
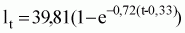
La ecuación de crecimiento ponderal calculada a partir de la expresión anterior y de las relaciones peso-talla es la siguiente:
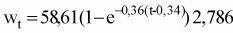
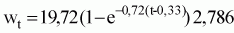
En el cuadro 4 se exponen los datos relativos al crecimiento en talla y peso del pulpo de acuerdo con la primera expresión calculada.
En la figura 3 se expresa el crecimiento en peso de Octopus vulgaris en este área.
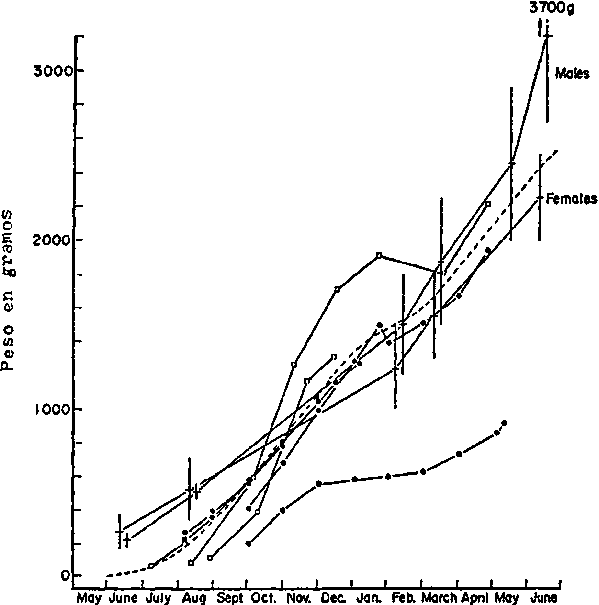
En la figura 4 se muestra el crecimiento de Octopus vulgaris en el Mediterráneo (Nixon, 1969) con el fin de poder compararlo con el del Atlántico Centro-oriental.
CONCLUSIONES
Se constata que en una población de Octopus vulgaris es posible diferenciar clases de edad.
Las ecuaciones que relacionan el peso y la talla son las siguientes:
|
Machos |
PT = 0,937 L2,699 |
|
Hembras |
PT = 1,110 L2,594 |
|
Total |
PT = 0,976 L2,691 y PT - 0,7844
L2,8814 |
Lt = 59,67 (1 - e-0,36 (t-0,34));
Lt= 39,81 (1 - e-0,72 (t-0,33))
Wt = 58,61 (1 - e-0,36 (t-0,34)) 2,786;
Wt = 19,7 (1 - e-0,72 (t-0,33)) 2,786
Se ha comprobado que el ciclo biológico de esta especie es generalmente inferior a dos años.
AGRADECIMIENTOS
Agradezoo a los doctores Bas, Morales, López Veiga y Gómez Larrañeta y a D. Germán Pérez-Gándaras sus valiosas sugerencias y consejos para la elaboración de este trabajo. A D. Xavier Fuste su colaboración en el análisis de las estadísticas del B/P "Galicia". A Aida Fernández su trabajo en la preparación de las gráficas, cuadros y texto del presente trabajo. Deseo expresar también mi agradecimiento a D. Fermín Salvatierra por la ayuda que me prestó durante los años de mi estancia en el Laboratorio de Barcelona.
|
NOTA: |
Este trabajo se preparó para la Tesis Doctoral
"Estudios sobre la biología y estructuras de las poblaciones del pulpo
común (Octopus vulgaris)" presentada en la Facultad de
Biología de la Universidad de Barcelona el 22 de julio de 1977. |
SUMMARY
On the age and growth of Octopus vulgaris in the Central-Eastern Atlantic (26°10'N-23°30'N).
In the present work the differentiation of age classes in Octopus vulgaris populations commercially exploited in the Central-Eastern Atlantic is obtained for the first time, following their evolution along the year. The method used is based on the analysis of size frequency distribution by means of techniques which permit to differentiate gaussian populations in polymodal distributions. Studies have been carried out on growth and age of this species, growth being expressed according to Van Bertalanffy equations and size-age classes being established. Size and weight growth rate have been also calculated being in agreement with those values obtained in the laboratory. Finally, the biological cycle of Octopus vulgaris has been verified to be usually less than two years.
Parameters of the two growth equations:
Weight-length expressions:L¥ (cm): 59,67 - 39,81
K: 0,36 - 0,72
to: 0,34 - 0,33
W¥ (kg): 58,1 - 19,75
Males: WT - 0,937 L2,699
Females: WT - 1,110 L2,594
Total: WT = 0,976 L2,691 and WT = 0,7844 L2,8814
BIBLIOGRAFIA
Battacharya, C.G.- 1967. A simple method of resolution of a distribution into gaussian components. Biometrics, 23: 115-135
Bertalanffy, L. von.- 1938. A quantitative theory of organic growth. Hum.Biol., 10: 181-213
Boletzky, S. von.- 1974. The "larvae" of Cephalopoda. A review. Thalassia Jugoslavica, 10: 45-76
Buchanan-Wollaston, H.J. y W.C. Hodgson.- 1929. A new method of treating frequency curves in fishery statistics, with some results. J.Cons.Exp.Mar, 4: 207-223
Cassie, R.M.- 1954. Some use of probability paper in the analysis of size frequency distribution. Ars.J.Mar.Freshwater Res., 5: 513-522
Clarke, M.R.- 1965. "Growth rings" in the beaks of the squid Moroteuthis ingens (Oegopsida: Onychoteuthidae). Malacologia. 3(2): 287-307
Guerra, A.- 1975. Determinación de las diferentes fases del desarrollo sexual de Octopus vulgaris Lam. mediante un índice de madurez. Inv.Pesq., 39 (2): 397-416
Guerra, A.- Pitting a von Bertalanffy expression to Octopus vulgaris growth. Inv.Pesq., (en prensa)
Guerra, A.- 1978 c. Estructura de la población de Octopus vulgaris del Atlántico Centro-oriental (26°10'N-23°30'N). Working Group for evaluation of cephalopod stocks in CECAF Region. Tenerife (mimeo)
Gulland, J.A.- 1975. Manual of Methods for fish stock assessment. 3rd Ed. FAO Manual in Fisheries Science. 4
Harding, J.P.- 1949. The use of probability paper for graphical analysis of polimodal frequency distributions. J.Mar.Biol.Ass.U.K., 28: 141-153
Ikeda, I. y H. Hatanaka.- 1971. Quelques observations sur Octopus vulgaris Cuvier au large de la côte nord-ouest de l'Afrique. FAO Fish.Rep., 10: 100-104
Itami, K., Y. Izawa, S. Maeda y K. Nakai.- 1963. Notes on the laboratory culture of the Octopus larvae. Bull.Jap.Soc.Scient.Fish., 29: 514-520
Lipinsky, M.- 1977. The age of squid, Illex illecebrosus (le Sueur, 1821) from their statoliths. ICNAF Res.Doc., 78/11/15
Mangold-Wirz, K.- 1963. Biologie des céphalopodes benthiques et nectoniques de la mer Catalane. Vie et Milieu. 13: 385 pp.
Mangold, K. y S.V. Boletzky.- 1973. New data on reproductive biology and growth of Octopus vulgaris. Mar.Biol., 19: 7-12
Nixon, M.- 1969. The lifespan of Octopus vulgaris Lam. Proc.M.Soc.Lond., 38: 529-540
Nixon, M.- 1971. Some parameters of growth in Octopus vulgaris. J.Zool.Lond.. 163: 277-284
Rees, W. J.- 1950. The distribution of Octopus vulgaris Lamarck in the British waters. J.Mar.Biol.Ass.U.K., 29: 361-378
Ricker, W.E.- 1975. Computation and interpretation of Biological Statistics of Fish Populations. Bull.Fish.Res.Bd.Canada, 191: 382 pp.
Tanaka, J.- 1958. On the stock of Octopus vulgaris Lam, on the East Coast of Böso Peninsula, Japan. Ball.Japan Soc.Sci.Fish., 24(8): 601-607
Wodinsky, J.- 1972. Breeding season of Octopus vulgaris. Mar.Biol., 16: 59-63
CUADRO 3
Talla media y edad para Octopus vulgaris del
Atlántico
|
Linea |
Mes |
Talla (cm) |
Edad (meses) |
|
A
|
sep. |
6.3 |
6 |
|
oct. |
7.8 |
7-8 |
|
|
nov. |
9.5 |
8-9 |
|
|
dic. |
10.4 |
10 |
|
|
B
|
abr. |
6.4 |
7-8 |
|
may. |
8.0 |
8-9 |
|
|
jun. |
9.0 |
10 |
|
|
jul. |
8.4 |
9-9 |
|
|
ago. |
10.7 |
10 |
|
|
sep. |
11.7 |
11-12 |
|
|
oct. |
14.4 |
14 |
|
|
nov. |
16.0 |
15 |
|
|
C
|
abr. |
11.5 |
11-12 |
|
may. |
13.0 |
13 |
|
|
jun. |
14.5 |
14 |
|
|
jul. |
16.0 |
15 |
|
|
ago. |
17.0 |
16 |
|
|
sept. |
17.9 |
17-18 |
|
|
oct. |
19.8 |
19-20 |
|
|
nov. |
22.2 |
21-22 |
|
|
D
|
ene. |
12.0 |
12-13 |
|
feb. |
14.2 |
14 |
|
|
mar. |
14.0 |
14 |
|
|
abr. |
18.7 |
18 |
|
|
may. |
19.3 |
19 |
|
|
jun. |
19.9 |
19-20 |
|
|
jul. |
20.3 |
20 |
|
|
ago. |
22.6 |
21-22 |
|
|
sep. |
23.0 |
23 |
|
|
oct. |
24.0 |
23-24 |
|
|
E
|
ene. |
21.0 |
18-19 |
|
feb. |
21.8 |
20-21 |
|
|
mar. |
22.1 |
21-22 |
|
|
abr. |
24.7 |
23-24 |
|
EDAD (meses) |
TALLA (en) |
A PESO (granos) |
E PESO (gramos) |
PROMEDIO |
|
7 |
5,0 |
74,2 |
80,9 |
77,5 |
|
8 |
6,6 |
156,6 |
180,1 |
168,3 |
|
9 |
8,2 |
280,8 |
336,5 |
308,6 |
|
10 |
9,7 |
441,4 |
546,0 |
493,7 |
|
11 |
11,1 |
634,5 |
805,2 |
719,8 |
|
12 |
12,6 |
892,3 |
1 160,1 |
1 026,1 |
|
13 |
13,9 |
1 162,2 |
1 539,4 |
1 350,8 |
|
14 |
15,3 |
1 504,7 |
2 029,6 |
1 767,1 |
|
15 |
16,6 |
1 873,9 |
2 567 |
2 220,5 |
|
16 |
17,9 |
2 295,5 |
3 189,9 |
2 742,7 |
|
17 |
19,1 |
2 733,4 |
3 845,7 |
3 289,5 |
|
18 |
20,3 |
3 220,5 |
4 583,6 |
3 902,0 |
|
19 |
21,5 |
3 758,7 |
5 408,4 |
4 583,5 |
|
20 |
22,6 |
4 298,8 |
6 244,6 |
5 271,7 |
|
21 |
23,7 |
4 885,4 |
7 160,8 |
6 023,1 |
|
22 |
24,7 |
5 460,1 |
8 066,3 |
6 763,2 |
|
25 |
28,1 |
7 681,2 |
11 624,2 |
9 652,7 |
|
36 |
37,0 |
16 198,7 |
25 840,7 |
21 019,7 |
|
48 |
43,5 |
25 106,7 |
41 355,0 |
33 230,8 |
|
60 |
48,3 |
33 241,2 |
55 788,5 |
44 514,7 |
|
72 |
51,9 |
40 289,3 |
66 541,6 |
54 415,4 |
|
84 |
54,3 |
45 477,4 |
78 132,3 |
61 754,8 |
|
96 |
56,1 |
49 625,0 |
85 675,2 |
67 650,1 |
|
108 |
57,3 |
52 509,2 |
91 017,1 |
71 763,1 |
|
120 |
57,9 |
54 002,5 |
93 790,2 |
73 896,7 |
Ecuaciones utilizadas: para la talla 1t = 59,67 (1 - e 0,36 (t-0,34))
Para el grupo de pesos A: PT = 0,976 L2,691 Y para B: PT = 0,784 L2,881
Fig. 1. - Relaciones talla-peso de Octopus vulgaris. Puntos: Mediterráneo catalán. Triángulos: Atlántico Centro-oriental.
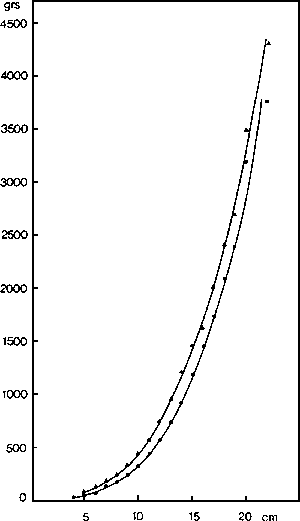
Fig. 2. - Tallas medias mensuales para cada grupo de edad derivado de las frecuencias de tallas de Octupus vulgaris del Atlántico Centro-oriental.
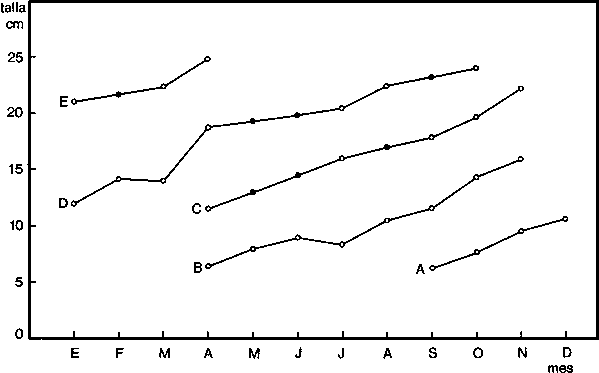
Fig. 3. - Crecimieinto en peso de Octopus vulgaris da la plataforma sahariana
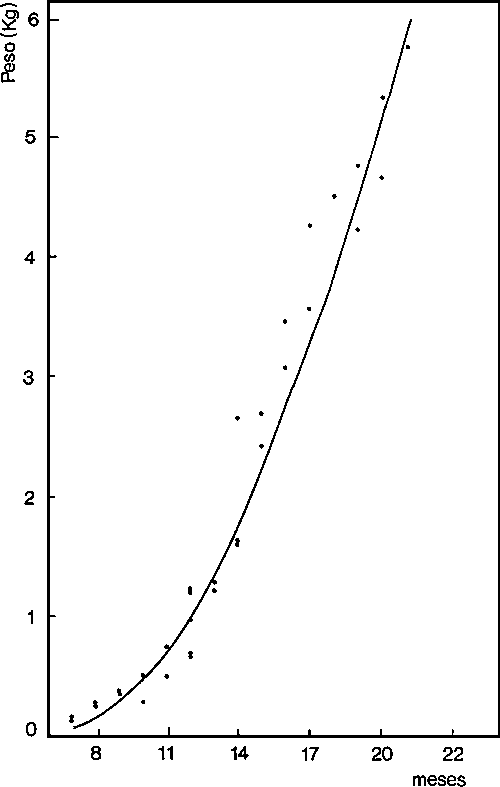
Figura 4.- Crecimiento de
Octopus vulgaris en el Mediterráneo, Curve
hipotótice del crecimiento (-----) extrapolada de todos los demás
datos. · NIKON (1966) a partir de
ejemplares individuales. o NIXON (1966; promedio de cuatro pulpos.
 Lo BIANCO (1908) a partir de animales
individuales. + derivado de (...) (1963) a partir de grandes muestras; se
indica la media y 1a desviación típica. (Tomado de NIXON,
1969)
Lo BIANCO (1908) a partir de animales
individuales. + derivado de (...) (1963) a partir de grandes muestras; se
indica la media y 1a desviación típica. (Tomado de NIXON,
1969)