Este es uno de los parámetros básicos en dinámica de poblaciones. Su estudio es menos crítico que el de la mortalidad porque los resultados son más fáciles de obtener, y los modelos analíticos son más robustos en lo que concierne a parámetros de crecimiento que a los de mortalidad. Como regla se estudia el crecimiento individual, y el crecimiento de la población se considera sólo una simple adición de sus componentes individuales. En el caso de los peneidos, surgen diversas dificultades:
Los crustáceos carecen de una estructura ósea que registra una huella de variaciones del ambiente interno y externo capaz de permitir una lectura directa de la edad. No obstante debemos señalar que según Yano y Kobashi (1969), el número de lamelas en la endontícula aumenta con la talla, ofreciendo alguna posibilidad de lectura de la edad.
El crecimiento es discontinuo y la aparición de mudas convierte en delicadas las técnicas de marcado y, en particular, el uso de marcas externas (discos de Petersen, etc.). Según Bodeke, Dijkema y Siemelink (1977), el crecimiento en longitud continúa durante el período intermudas por alargamiento de las partes flexibles del caparazón, mientras que el tamaño de los escudos dorso-laterales se mantiene inalterado. Más aún, ellos demostraron que la relación entre la longitud del caparazón y la longitud total variaba de forma cíclica entre dos mudas.
Como muchas especies tropicales, los camarones peneidos muestran frecuentemente un período de reproducción continuo que hace difícil el uso de los métodos de descomposición de las curvas polimodales de distribución de frecuencias de tallas.
Los trabajos básicos sobre este tema son abundantes y pueden consultarse, entre otros, los de Kurata (1962) y Mauchline (1977) para el estudio de las mudas y el crecimiento en los crustáceos y, para estudios más generales de crecimiento, los de von Bertalanffy (1938, 1964), Walford (1946), Gulland y Holt (1959), Tomlinson y Abramson (1961), Fabens (1965), Southward y Chapman (1965) y Ebert (1973), sin olvidar las obras clásicas de Beverton y Holt (1956), Gulland (1969), Ricker (1975) y la excelente síntesis de Ricker (1979).
La estimación de los parámetros de crecimiento se efectúa en dos etapas. Primero deben recopilarse los datos básicos (claves talla-edad, tasas instantáneas de incremento de tallas medias, etc.). Luego, esta información debe ser expresada eventualmente por una expresión matemática más o menos simple (de tipo logística, linear, monomolecular, etc.). Esta segunda etapa es cada vez más opcional, desde que el uso corriente de computadoras permite que las claves talla-edad observadas sean utilizadas directamente. La fórmula es en cualquier caso aproximada, ya que una sóla ley matemática puede raramente ser aplicada al crecimiento de un ejemplar desde su nacimiento hasta su muerte y el precio a pagar por la simplicidad es un cierto grado de aproximación. Debe recordarse también que, según Knight (1968), los parámetros calculados no tienen significado biológico, punto de vista contestado por Kruger (1969, citado por Ricker, 1979).
5.1.1 El Método de las Progresiones Modales
Este método, cuyo origen se remonta a Petersen, consiste en el seguimiento a lo largo del tiempo de las modas observadas en las distribuciones de tallas de muestras tomadas periódicamente de las capturas. Entre los peneidos, donde la edad absoluta se desconoce, se define una edad relativa comenzando desde un punto arbitrario (talla de reclutamiento, la primera moda observada, etc.). Más tarde, los datos complementarios sobre la fase juvenil permitirán quizás revisar estas edades relativas y relacionarlas a la fecha o período de nacimiento, cuando ello parezca ser necesario.
La limitación principal de este método se encuentra en la dificultad que reviste identificar, en peneidos costeros, grupos de tallas diferenciados y seguirlos a lo largo del tiempo (Figura 32). No obstante, con un poco de experiencia se pueden obtener en algunos casos ciertos éxitos, de los que existen varios ejemplos (Neiva, Dos Santos y Jankauskis, 1971; Galois, 1975; García, 1975; Edwards, 1977). La facilidad del análisis dependerá del esquema anual de reproducción y de la calidad del muestreo.
En áreas de fuertes fluctuaciones estacionales en la producción, se puede seguir la cohorte principal (o grupo de cohortes); en estuarios, donde el crecimiento es muy rápido, un muestreo minucioso y frecuente (una vez por semana) hace a menudo posible la observación de micro-cohortes, generadas por el ciclo lunar (mareal) del reclutamiento larvario a las zonas de alevinaje.
A veces es posible descomponer la distribución total de tallas en una serie de distribuciones simples, cada una representando una cohorte diferente, usando uno de los muchos métodos disponibles, más o menos sosfisticados (Harding, 1949; Cassie, 1954; Tanaka, 1956; Battacharya, 1967; Hasselblad, 1966; Gueno y Le Guen 1968; Gregor, 1969). También son útiles algunos programas recopilados por MacDonald (1969). Tan sólo los métodos más simples han sido utilizados para peneidos (Cassie y Gueno-Le Guen) y, a primera vista, los resultados no son siempre indiscutibles. No obstante, en Côte d'Ivoire el crecimiento del Penaeus notialis calculado con la ayuda del método de análisis de las progresiones de modas ha sido verificado usando las técnicas de marcado (García, 1975).
El mayor inconveniente de todos estos métodos es su subjetividad evidente u oculta. Destinados originalmente para evaluar el número de individuos de clases de edad gráficamente distintas, se usan demasiado frecuentemente para subdividir curvas de frecuencias de tallas cuya estructura es evidente. Esta distorsión en el uso de los métodos puede causar serios errores.
La posibilidad del estudio del crecimiento de camarones por análisis de la progresión de modas, en unos animales de crecimiento rápido y continua reproducción, depende mucho de la configuración espacio-temporal del muestreo y de la precisión de las medidas. En particular, las medidas precisas (longitud del caparazón a 1/10 mm) permiten una discriminación mayor de las modas de las grandes tallas. Las medidas se hacen frecuentemente con calibradores normales, pero Cole y Mistakidis (1953) y Mauchline (1958) han propuesto instrumentos de alta precisión, que son de gran utilidad para mediciones de tallas de pequeños individuos.
La existencia de una distribución geográfica o batimétrica heterogénea de tallas y sexos es sin duda un obstáculo que hace difícil elaborar la reconstrucción de un histograma representativo de la población. Esta es la razón de las dificultades que surgen generalmente en los análisis de muestras de las pesquerías industriales. Las variaciones en la concentración relativa del esfuerzo sobre los diferentes estratos de la población, asociadas con variaciones en capturabilidad, producen a veces cambios en la forma de los histogramas de distribuciones de tallas de la captura de una marea a otra, que no están relacionados con el crecimiento, sino con el carácter no aleatorio del “muestreo” realizado por el barco de pesca. Esta dificultad se puede obviar si se utiliza un buque de investigación con un esquema de muestreo adecuado (muestreo estratificado).
Las observaciones efectuadas sobre el crecimiento de los subadultos en migración (Loesch, 1965; Lhomme, 1979) son particularmente difíciles de interpretar. De hecho, y en sentido absoluto, si la migración de los juveniles hacia el mar tiene lugar a una talla determinada, se observarían modas fijas y aparentemente no habrían crecimientos. Por otro lado, si la migración sucede en un determinado estado de desarrollo (por ejemplo el estado de maduración), la talla de migración variará en función de las condiciones de crecimiento que existen en las diferentes partes del estuario y en distintas estaciones. Si la talla para la migración depende de la duración de la estancia en el estuario, en si mismo dominado por las condiciones ambientales, ésta variará en función de los factores ambientales y, en particular, de la salinidad (García, 1977; Le Reste, 1979) o de la temperatura (Trent, 1967).
Las poblaciones migratorias están formadas generalmente por numerosas micro-cohortes1 y, a menos que exista un muestreo bien definido que permita su identificación, la atribución de variaciones en talla media de migración a un crecimiento, puede conducir a resultados erróneos, que generalmente subestimarán el crecimiento real. Este tipo de datos debe por lo tanto ser considerado con prudencia.
5.1.2 Marcado
La dificultad para identificar los grupos de edades en los camarones puede ser resuelta por el uso de técnicas de marcado. El principio se basa en que un ejemplar o grupos de ejemplares pueden ser identificados con una marca visible y el crecimiento puede determinarse entre su marcado y recaptura considerando, según la hipótesis básica, que la marca no afecta al crecimiento.
Las inyecciones colorantes, debidamente utilizadas, no afectan al metabolismo (cf. Capítulo 6). Se usan para el marcado de grupos extraídos de la captura, con un rango de tallas limitado, donde se puede hacer un seguimiento de la evolución de la talla media. Para cubrir toda la gama de tallas presentes en la población, es necesario multiplicar las operaciones de marcado con inyecciones de colores diferentes. El uso simultáneo de marcas secundarias (Sección 6.5) aumenta considerablemente el número de combinaciones posibles. Las marcas secundarias e internas de plástico, numeradas, permiten incluso la identificación de los individuos. Una ventaja adicional de las marcas externas (discos de Petersen y derivados) es que permiten el marcado de todas las tallas capturadas sin previa clasificación y con una identificación individual. Entonces son posibles todos los tipos de estratificación cuando los datos son procesados: por grupos de tamaños, sexo, a veces por estados sexuales, etc.
1 Pequeños grupos con diferentes orígenes espacio-temporales
A pesar de que la técnica de inyección colorante debidamente aplicada sea probablemente la más inofensiva, las marcas externas dan más posibilidades para la interpretación. Los principales datos obtenidos por marcado son: la talla de marcado, la talla de recaptura, por lo tanto el crecimiento, y tiempo en libertad. Desde que la recaptura se lleva a cabo por pescadores, el tiempo en libertad es extremadamente variable para el mismo lote de individuos marcados.
5.1.3 Crecimiento de Machos
Su crecimiento es normalmente menor que el de las hembras (una L∞ inferior y una K superior -ver Sección 5.2). En consecuencia, las frecuencias de distribuciones de tallas contienen un rango menor de tallas y son, por lo tanto, más difíciles de analizar que las hembras, ya que son más compactas. No obstante, cuando se conoce la curva de crecimiento y la relación talla-edad, García (1975) demostró que se podría usar una relación entre la talla media de machos y hembras para deducir la relación talla-edad de los machos y su curva de crecimiento.
Tal relación se obtiene representando la talla media de los machos de una muestra (por ejemplo de un arrastre a una determinada profundidad) como una función de la talla media de las hembras de la misma muestra, para una serie de muestras tomadas en diferentes estaciones de arrastre. La dispersión de los puntos es lo suficientemente pequeña como para trazar la curva a ojo. La Figura 33 muestra la curva obtenida por García (1975) para Penaeus notialis y, a título comparativo, la proporcionada por Iversen, Jones e Idyll (1960) para Penaeus duorarum.
Si se admite que la distribución diferencial media observada en las tallas de camarones en el fondo (Figura 15) refleja una distribución ligada a la edad, y que los machos y hembras capturados conjuntamente son por término medio de la misma edad, a pesar de las posibles variaciones en la relación de sexos, se puede pasar simplemente de la clave talla-edad de las hembras (si se conoce) a la de los machos.
En Côte d'Ivoire este método dio resultados idénticos a aquellos obtenidos con el método de Petersen y por técnicas de marcado (García, 1975 y 1975a). Lhomme (1977a) utilizó el mismo método en Senegal, con la misma especie.
Cuando las progresiones modales “observadas” para los machos no son muy obvias, como a menudo es el caso, este método puede ayudar a evitar grandes errores.
5.1.4 Concepto de Edad Máxima
Ya que la edad del camarón no puede ser determinada directamente y las cohortes son normalmente difíciles de seguir, la edad máxima es difícil de determinar.
El análisis de las curvas de crecimiento muestra unos valores de K más altos y unos valores de L∞ más bajos para los machos que para las hembras. El estudio de la evolución de la relación de sexos con la talla (Figura 30) muestra igualmente un claro predominio de hembras a partir de cierta talla. Estos datos han sido a veces usados, con otras especies marinas, para deducir una longevidad inferior en los machos (Beverton y Holt, 1959; Holt, 1962).
Un estudio de la relación de sexos en función de la edad en P. notialis en Côte d'Ivoire durante un período completo de dos años, ha permitido demostrar que no hay una tendencia clara de este parámetro, y que la longevidad de los dos sexos se debe considerar comparable (Figura 34). Iversen e Idyll (1960) también demostraron que cuando se representa la relación de sexos frente al tamaño medio de las hembras de cada muestra de Peneaeus duorarum, no se observa tendencia alguna. Esta observación lleva a la misma conclusión de que la longevidad de machos y hembras es similar.
A título indicativo de la edad máxima, el camarón de más de dos años de edad se encuentra raramente en cantidades significativas en las capturas a pesar de que, en experimentos de marcado, se han observado camarones de al menos 27 meses de vida (Baxter, 1971).
Una vez que los datos básicos (talla-edad, crecimiento en función del tamaño) han sido obtenidos, puede ser necesario buscar una expresión matemática, el modelo, que permita la mejor expresión posible de crecimiento usando una fórmula simple. La bibliografía es rica en trabajos básicos en los que se analiza este tema, no siendo necesario hacer aquí un repaso exhaustivo. El lector podría referirse útilmente a trabajos básicos como los de Beverton y Holt (1956), Ricker (1958, 1975 y 1979) y Gulland (1969). Es raro que un solo modelo sea suficiente para representar el crecimiento de un ejemplar desde su nacimiento hasta su muerte, por lo que a menudo se debe aceptar una aproximación.
El modelo más frecuentemente usado es el de von Bertalanffy (1938), por lo que Beverton y Holt (1956) decidieron integrarlo en sus ecuaciones de rendimiento. Otros modelos han sido propuestos, como el de Gompertz (Riffenburgh, 1960), el logístico (Ricker, 1971) y el modelo exponencial (Ricker, 1958). Las propiedades del modelo de von Bertalanffy han sido estudiadas por un cierto número de autores, ya citados, y por Fabens (1965) y Southward y Chapman (1965). Los modelos de Gompertz y von Bertalanffy han sido confrontados por Silliman (1969) y Parrack (1979) en peces y peneidos respectivamente. Sus resultados demuestran que el modelo de von Bertalanffy, tal y como se usa en la actualidad, es apropiado. Diversos autores han propuesto algunas modificaciones, o una generalización, de la ecuación de von Bertalanffy (Richards, 1959; Chapman, 1961; Taylor, 1962). Estas no parecen todavía haber sido utilizadas, a pesar de ser posible su aplicación a los modelos de Beverton y Holt (Paulik y Gales, 1964). Knight (1969) también ha propuesto una ecuación modificada en la cual la verdadera tasa de crecimiento (crecimiento por unidad de tiempo) aparece como un parámetro.
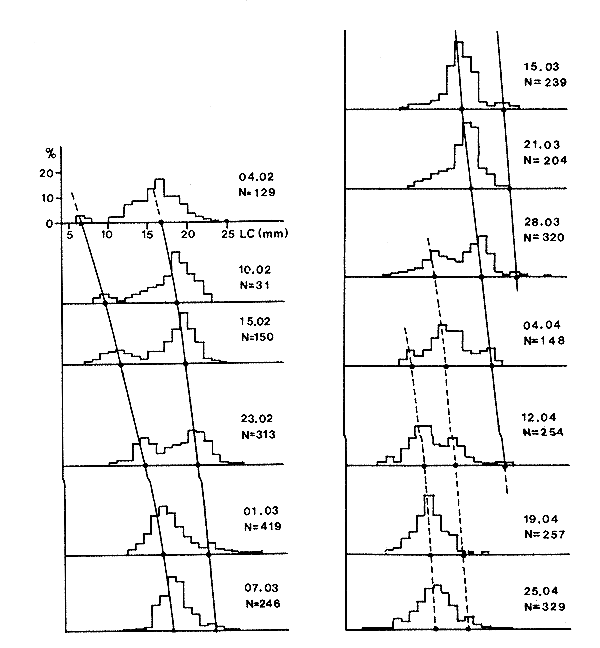
Figura 32 Crecimiento de Penaeus notialis en la laguna de Ebrie (según Galois, 1975)
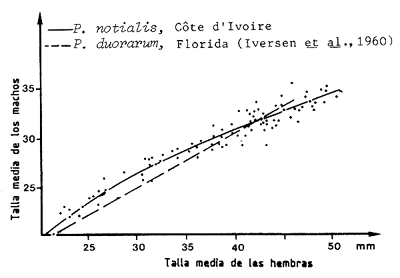
Figura 33 Relación entre la talla media de las hembras y la de los machos, para Penaeus notialis (según García, 1975) y para Penaeus duorarum (tomado de Iversen et al., 1960)
No insistiremos en el importante significado biológico que von Bertalanffy (1938, 1964) deseó atribuir a su modelo y que Ricker (1975) y otros (citados por Von Bertalanffy, 1964) han contestado. Hemos notado, con Ricker, que el modelo propuesto concuerda más frecuentemente con lo que se observa y, por lo tanto, puede ser aplicado como un modelo empírico, opinión compartida por Brody (citado por Ricker, 1975) quien estableció las bases del modelo.
Tan sólo nos referiremos aquí al modelo de von Bertalanffy y repasaremos brevemente los métodos utilizados comúnmente para calcular los parámetros de la ecuación. La expresión clásica de la curva de von Bertalanffy es de la siguiente forma:
| lt = L∞(l-e-K(t-to)) | (5.1) |
donde L∞ es la talla asintótica media hacia la que tiende el individuo. En este punto debemos señalar que el principio mismo del crecimiento asintótico ha sido a veces cuestionado (Knight, 1968; Ricker, 1979).
K es el coeficiente de crecimiento de Brody (Ricker, 1975) señaló que es inapropiado hablar de “tasa de crecimiento” para este parámetro) y to es la edad teórica de los individuos cuando la talla es cero. Existen numerosos métodos para calcular los parámetros.
5.2.1 El Método de Ford-Walford (1946)
Este se basa en la siguiente forma de ecuación de von Bertalanffy (Ford, 1933):
| lt + l = L∞ (l-k) + klt | (5.2) |
donde k, el coeficiente de crecimiento de Ford, es igual a e-K. Walford demostró que la recta de ajuste de lt+l sobre lt , de pendiente k, corta a la bisectríz de 45o en lt = L∞ (Figura 35A). Beverton (1954 citado por Ricker, 1975) propuso que el valor obtenido para L∞ solo debería ser considerado provisional y que Loge (L∞ - lt) debería ser expresado como una función de t ya que:
| Loge (L∞ - lt) = Loge L∞ + Kto - Kt | (5.3) |
La linearidad de esta relación es sensible a pequeñas variaciones de L∞, y algunas pruebas con L∞ ligeramente diferentes ayudarán a determinar un valor más exacto de este parámetro (Figura 35B). La pendiente de la relación (que en este caso es una regresión clásica si t se conoce con precisión) es igual K y la ordenada en el origen igual a (Loge L∞ + Kto) permite obtener to.
Ricklef (1967) también propuso un método gráfico aproximativo, a partir de un enfoque similar, expresando en peso las curvas de Gompertz, de von Bertalanffy y las logísticas. Este método se utiliza poco.
Gulland (1969) demostró que to puede también obtenerse gráficamente partiendo de los mismos elementos. En efecto, según la ecuación expresada más arriba, cuando lt = 0 (y por definición t = to) la ordenada es igual a Loge L∞. En consecuencia, cuando Loge (L∞ - lt) se expresa como una función de t, el punto que tiene Loge L∞ como ordenada, tiene a to como abcisa (Figura 36).
Raramente se conoce la verdadera edad. Por ello es posible, o considerar que to = 0, o se toma como origen un punto observable del ciclo vital: por ejemplo, la migración. Entonces la edad media de migración se tomaría como el origen (t'o = 0) y, usando una edad relativa (t'), se definiría la curva de crecimiento como en las secciones precedentes. El cálculo real de esta edad media de migración, obtenida de los datos sobre la puesta y migración, permitirá ajustar la curva a una escala de tiempo real.
Desde que la edad de migración varía con las condiciones medio-ambientales del estuario, se puede utilizar como origen de las edades relativas la primera moda observada en las distribuciones de frecuencias de tallas en el mar. Este método fue utilizado por García (1970, 1975, 1977) y Galois (1975) para Penaeus notialis en Côte d'Ivoire y por Lhomme (1979) en Senegal, para la misma especie.
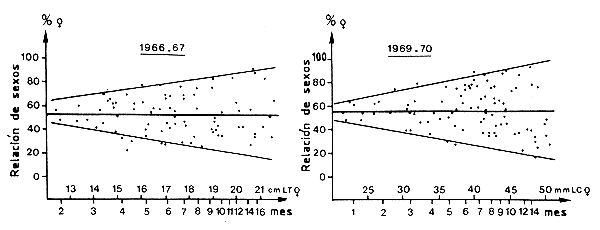
Figura 34 Variaciones de las relaciones de sexos en función de la edad o de la talla de las hembras en muestras recogidas en Côte d'Ivoire (según García, 1977)
 |  |
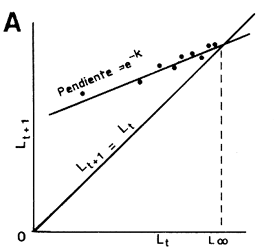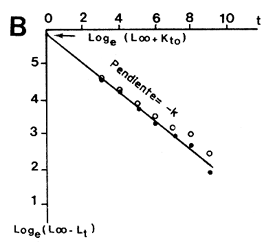Figura 35 Cálculo de los parámetros de la curva de crecimiento de von Bertalanffy
A. Método de Ford-Walford
B. Método de Beverton
(tomado de Ricker, 1975)
El método de Ford-Waldford ha sido adaptado por Manzer y Taylor (1947) para usar de datos de marcado. Cuando se dispone de ejemplares de diferente talla que hayan estado en libertad durante aproximadamente el mismo tiempo, se puede usar la gráfica de Ford-Waldford representando la talla de recaptura del ejemplar en función de la talla de puesta en libertad (Manzer y Taylor, 1947; Hancock, 1965). Este método fue utilizado para los camarones peneidos por Lindner (1953), Lindner y Anderson (1956), Iversen y Jones (1961), Kutkuhn (1962), Klima (1964, 1974), Berry (1967) y muchos otros. El procedimiento es relativamente simple. Los camarones recapturados se agrupan por idénticos intervalos de días en libertad, que deberán ser los más cortos posibles (una semana o diez días). Para cada período, se analiza la relación entre la talla de recaptura (Lt+10 días) y la talla de puesta en libertad (1t). Así se obtienen tantas curvas de crecimiento como intervalos de tiempo con suficientes recapturas para la estimación, lo que requiere que se hayan marcado tantos camarones como para asegurar un número suficiente de individuos cada período de recaptura.
5.2.2 El Método de Chapman (1961) (Figura 37)
Este método, atribuido a Chapman por Ricker (1979, p. 709), se le conoce frecuentemente por método de Gulland (1969). Se deriva de la siguiente forma de ecuación de von Bertalanffy:
| (1t+1-1t) = (L∞ -1t) (1 - e-K) | (5.4) |
La recta de regresión funcional de (1t+1 -1t) sobre 1t tiene una pendiente -(1 - e-K) y una abcisa en el orígen = L∞. Este método puede utilizarse con datos de marcado si el incremento de la talla por unidad de tiempo Δ L se expresa como una función de la talla media en el momento del marcado, y así el crecimiento es calculado desconociendo la edad real, lo que justifica el calificativo de “atélico” dado por Díaz (1963) para este método.
Si los períodos en libertad son desiguales, Gulland y Holt (1959) proponen un método de cálculo
basado en una corrección tangente hiperbólica. Este es particularmente valioso cuando el número de
recapturas es insuficiente para permitir un reagrupamiento en estratos de tiempo en libertad de
igual duración. El método ha sido explicado con detalle por Jones (1976). De forma esquemática, si
(a) es el período de tiempo en libertad, (y = (1t+a-1t)/a) el incremento por unidad de tiempo y (x)
la talla media ((1t+a +1t)/2) durante el período de libertad, se puede hacer, en una primera etapa,
la regresión de y sobre x, donde la pendiente dará un valor provisional de K. Si b = Ka/2, se pueden
corregir los incrementos observados y, haciendo la regresión de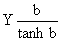 
sobre x, obtener un
segundo valor de K. El proceso se repite hasta que el valor de K se estabilice. Para cortos períodos de libertad (menos de 2 meses) no es necesaria la corrección y el valor de K se estabiliza desde el primer paso. Campbell y Phillips (1972) propusieron una solución diferente al mismo problema pero, según Ricker (1979), el método de Gulland y Holt (1959) es preferible cuando los intervalos de tiempo son largos.
5.2.3 Discusión sobre los Métodos de Regresión
Ricker (1975, p. 225) precisó que el uso directo de una regresión de 1t+1 sobre 1t no es satisfactoria, ya que las dos variables están sujetas a error, la distribución de los puntos a lo largo de la recta no es normal y todos los puntos son utilizados dos veces (como 1t y luego como 1t+1), excepto los dos extremos que se usan una sola vez. La modificación de Beverton (Sección 5.2.1) esta dirigida a superar esta dificultad. El problema es el mismo cuando se aplica el método de incrementos (Sección 5.2.2). Díaz (1963) utilizó una línea de regresión funcional (de Wald, 1940) más apropiada. Troadec (1968), como García, Petit y Troadec (1970) y García (1975), utilizaron un eje mayor reducido (o recta de Tessier). En su último manual, Ricker (1975), aplicando los resultados de su trabajo sobre el uso de regresiones en biología (Ricker, 1973), recomienda el uso de su último método y recuerda que Chapman (1961) había discutido ya la posibilidad de obtener por regresión, los parámetros de la ecuación de von Bertallanfy.
5.2.4 Los Métodos de Cálculo Automático
El uso corriente, y cada vez mayor, de ordenadores permite recurrir a unos métodos de cálculo que aportan estimaciones de la varianza de los parámetros. En el caso de los datos clásicos de crecimiento, el programa VONB de Allen (1966a) permite el uso de datos regular o irregularmente espaciados en el tiempo. En los programas BGC2 y BGC3 (Abramson, 1971), también pueden utilizarse respectivamente datos regular o irregularmente espaciados.
El programa CIAT D05 de Psaropoulos1 aplica el método de Tomlinson y Abramson (1961). Este programa fue utilizado por García (1975) para Penaeus notialis.
1 Disponible en el IATTC, La Jolla, California, USA
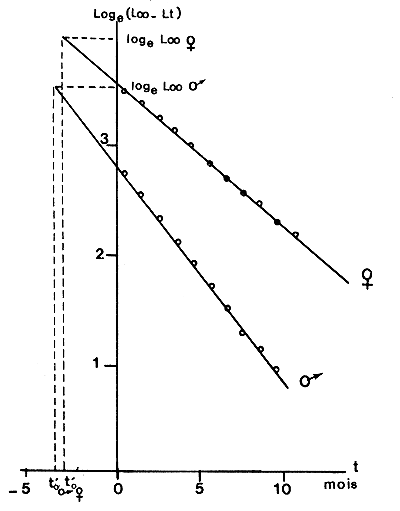
Figura 36 Determinación de t' Æ por el método de Gulland (1969) en Penaeus notialis. El origen de los ejes (t' = Æ) es arbitrario (ver texto)
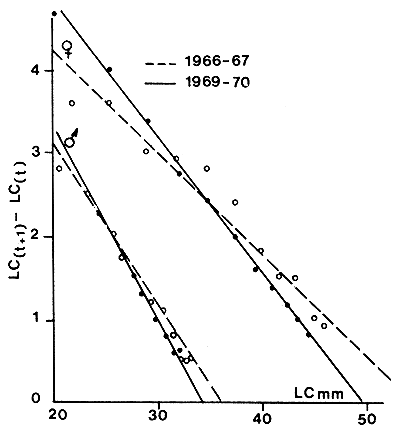
Figura 37 Cálculo de los parámetros de crecimiento por el método de Chapman (1961) en Penaeus notialis en Côte d'Ivoire
En lo que concierne al marcado, Fabes (1965) propuso un programa de cálculo2 que permite determinar los parámetros de la ecuación de crecimiento de la ecuación original de Brody por el método de los mínimos cuadrados. Un ejemplo de su utilización sobre camarones de Madagascar se puede encontrar en Le Reste y Marcille (1976). Este programa ha sido modificado por Allen (1967, programa FABVB) y por Tomlinson (en Abramson, 1971, programa BGC4). Southward y Chapman (1965) propusieron un programa para el cómputo de los cuatro parámetros de la ecuación de Richards (1959), por el método de los mínimos cuadrados.
5.2.5 Las Variaciones Estacionales de Crecimiento
La cuantificación de estas variaciones es particularmente importante en animales de corta vida. Estas pueden tener orígenes climáticos (Ikematsu, 1955; Lindner y Anderson, 1956; García, 1975, 1977; Lhomme, 1978a; Klima, 1980) (Figura 38) o biológicos y relacionados, por ejemplo, con la reproducción (García, 1975; Penn, 1975). Lhomme (1978a) demostró una relación entre el valor de K y la temperatura del medio, en Senegal (Figura 39). Una detallada revisión de este problema se encuentra en Ricker (1979).
Cuando existen estas variaciones, pueden complicar seriamente los estudios del crecimiento por análisis de la progresión de modas. Se pueden poner en evidencia mediante sucesivos marcados en diferentes estaciones. La consecuencia más grave de estas variaciones estacionales de la tasa de crecimiento es que cada cohorte de una generación anual tendrá un crecimiento diferente, según su fecha de nacimiento, y no habrá una clave talla-edad , sino tantas claves como cohortes elementales (12 cohortes mensuales, por ejemplo).
Hay que recordar que, a pesar de que esta posibilidad no ha sido empleada todavía en camarones, la ecuación de von Bertalanffy se puede adaptadar para expresar matemáticamente las variaciones estacionales (Lockwood, 1974). Por otra parte, Ursin (1963) ha propuesto la incorporación de temperatura al modelo de von Bertalanffy, estando entonces expresado el tiempo en días-grados.
Considerando la dificultad de analizar las distribuciones de tallas en peneidos, el marcado parece ser una técnica fundamental para analizar el crecimiento y sus variaciones estacionales, a pesar de las restricciones mencionadas en el capítulo sobre las técnicas de marcado y su efecto en el metabolismo.
El uso directo de los datos observados, por ejemplo en modelos de simulación, ayudará a evitar el uso de ecuaciones muy complejas y ecuaciones aproximadas para describir el crecimiento.
Al estar relacionado el crecimiento con las condiciones ambientales, es extremadamente importante determinar las condiciones hidroclimáticas acompañantes para permitir eventuales comparaciones de los resultados de una región con otra.
Antes de su incorporación a los modelos, la ecuación de von Bertalanffy expresada en talla, deberá ser convertida en una ecuación expresada en peso de la siguiente forma:
| wt = Woo (1 - e-K(t - t)o)n | (5.5) |
donde n es el exponente de la relación talla-peso.
Se debe recordar que la ecuación puede ser también calculada directamente si se dispone de los datos peso-edad, como en la Sección 5.2.1 (Ricker, 1975, p. 231), usando la regresión de loge (Woo - wt) sobre t, donde la linearidad es muy sensible a pequeñas variaciones de Woo y donde la pendiente es igual a K. Kutkuhn (1966) utilizó el método de Allen (1967) para P. duorarum efectuando la regresión de W1/3 (t+1) sobre W1/3t.
El uso de este tipo de curva implica que el crecimiento es tratado como una función continua. Debido a la muda, sería quizás más juicioso el uso de funciones en escalera. Ya que la muda no es simultánea en todos los ejemplares, y el crecimiento parcial continúa durante el período de intermudas (Bodeke, Dijkema y Siemelink, 1977), la aproximación por una función continua no introducirá un sesgo considerable. Es necesario notar que en regiones frías, donde hay un período de intermuda prolongado (varios meses) en comparación con el intervalo básico de tiempo (un año), uno se aproxima más a las condiciones de muda “simultánea” y esta se convierte en un importante componente estacional de la evolución de las biomasas. Unos ejemplos de aproximaciones realizadas en estos casos para otros crustáceos pueden encontrarse en Kurata (1962), Hepper (1967) citado por Conan y Gundersen (1979) y Conan (1975). Este último autor demuestra el sesgo que resulta del uso de la curva de Von Bertalanffy por comparación con un modelo de simulación “en escalera”.
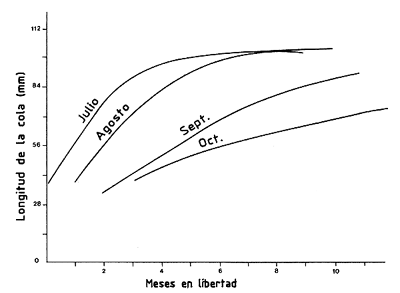
Figura 38 Curvas de crecimiento de diferentes cohortes de Penaeus setiferus en el golfo de México (según Klima, 1980)
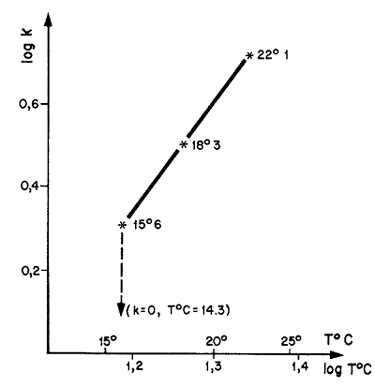
Figura 39 Variaciones de K en función de la temperatura, en Senegal (según Lhomme, 1979)
