3.1 Crecimiento en longitud y peso
3.2 Conversión de longitud a edad
3.3 Ejercicios
Para el análisis de poblaciones conviene expresar el crecimiento de los peces en forma de una expresión matemática. El requisito básico es obtener una expresión que dé el tamaño (en longitud o en peso) de un pez a una edad determinada cualquiera, esa expresión debe estar de acuerdo con los datos observados sobre tamaños o pesos a ciertas edades, y debe tener una forma matemática que pueda ser incorporada con suficiente facilidad en las expresiones que den el rendimiento. Estrictamente, la mayoría de los análisis de poblaciones están interesados más directamente en las tasas de crecimiento, es decir, en el aumento en peso o en longitud por unidad de tiempo, más que en el tamaño a diferentes edades, debido a que muchos de los problemas que se plantean en la evaluación de las pesquerías son esencialmente problemas de comparación del peso ganado por la población debido al crecimiento, y el peso perdido por mortalidad natural. Algunas veces, por ejemplo cuando se considera el efecto de un aumento en el tamaño de primera captura, es particularmente importante conocer la tasa de crecimiento durante un período de la vida relativamente corto, es decir, conocer cuánto tiempo necesitará el pez para aumentar del peso antiguo de primera captura al nuevo peso. Hay, por lo tanto, buenas razones para preferir, permaneciendo igual todo lo demás, un método de ajuste de ecuaciones a tasas de crecimiento, más que a datos de tamaños a ciertas edades.
Otras características deseables en una ecuación de crecimiento son que el trabajo necesario para ajustarla a los datos observados no sea mucho; que el número de las constantes utilizadas sea pequeño; que siempre que sea posible esas constantes tengan un significado biológico; y que, si se extrapola hasta edades más allá de las usadas al ajustarlas, no lleve a resultados poco razonables.
Existe una considerable cantidad - cada vez mayor - de trabajos y publicaciones sobre ecuaciones de crecimiento que abarcan una amplia gama de ecuaciones posibles, ninguna de las cuales parece ser enteramente satisfactoria en todas las situaciones. En realidad, es improbable que una fórmula simple sea siempre capaz de describir el crecimiento de un solo pez a lo largo de la mayor parte de su vida, durante la cual pueden existir grandes diferencias en las condiciones de disponibilidad de alimentos, esfuerzo reproductivo, etc. Estas notas no pretenden dar una reseña completa de las ecuaciones de crecimiento, sino que se ocuparán principalmente de una ecuación particular, la debida a VON BERTALANFFY, que satisface los dos criterios más importantes: se ajusta a la mayoría de los datos observados de crecimiento de peces, y puede incorporarse fácilmente a modelos para evaluación de poblaciones.
Si los valores de la longitud de un pez, crustáceo, o lamelibranquio, se indican gráficamente en función de la edad, se obtiene generalmente una curva, cuya pendiente disminuye continuamente al ir aumentando la edad, y que va aproximándose a una asíntota superior, paralela al eje de las X (véase fig. 3a). Las curvas de peso respecto a la edad también tienden a un valor asintótico superior, pero forman generalmente una curva sigmoidal asimétrica, la cual tiene su inflexión en un punto equivalente a un tercio del peso asintótico (véase fig. 3b).
Si se trazan gráficamente los valores de la tasa de crecimiento en longitud,
es decir, de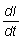 , respecto a la
longitud, el resultado, con frecuencia, viene representado por una línea
recta que corta al eje de las X en un punto L¥
más allá del cual el pez no crecerá. Este corresponde generalmente
a la asíntota del gráfico de longitud respecto a edad. Si la tasa
de aumento de longitud está relacionada linealmente con la longitud,
entonces, en términos matemáticos, se puede escribir:
, respecto a la
longitud, el resultado, con frecuencia, viene representado por una línea
recta que corta al eje de las X en un punto L¥
más allá del cual el pez no crecerá. Este corresponde generalmente
a la asíntota del gráfico de longitud respecto a edad. Si la tasa
de aumento de longitud está relacionada linealmente con la longitud,
entonces, en términos matemáticos, se puede escribir:
(3.1)
en la cual L¥ es el valor de l
para el que la tasa de crecimiento es nula. La forma general de esta ecuación
es una relación en línea recta, y = ax + b, con a =
- K, b = KL¥ . Para integrar
esta ecuación diferencial, la escribiremos en la forma 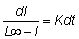 (véase sección 1), y, por tanto, -log (L¥
- l) = Kt + constante, o L¥
- l = e-Kt multiplicado por la constante, o
l = L¥ - constante multiplicado
por e-Kt.
(véase sección 1), y, por tanto, -log (L¥
- l) = Kt + constante, o L¥
- l = e-Kt multiplicado por la constante, o
l = L¥ - constante multiplicado
por e-Kt.
Poniendo t0 como la edad teórica en la cual l = 0, podemos obtener el valor de la constante de la relación
o1 = L¥ - constante
multiplicado por 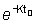 o constante
o constante
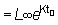 y entonces tenemos
y entonces tenemos
(3.2)
La ecuación (3.1) es idéntica a la deducida por VON BERTALANFFY basada en hipótesis fisiológicas. Este consideró que el crecimiento en peso era el resultado de la diferencia entre factores anabólicos y catabólicos, considerados como proporcionales a la superficie s y al peso w, respectivamente. Es decir:
o, poniendo w¥ a l3, s¥ l2
FIG. 3
a) Curva de crecimiento en longitud
b) Curva de crecimiento en peso
Al ajustar la curva de crecimiento, la tasa instantánea de crecimiento
será desconocida y sólo se conocerán las longitudes en
ciertos momentos, a menudo con un intervalo de un año cuando se deriven
de determinaciones de edades, y a intervalos irregulares si se derivan de datos
de marcaciones. Si los instantes t1 y t2
están próximos, se obtendrá una buena aproximación
a la tasa instantánea de crecimiento mediante 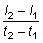 ,
en donde l1, l2 son las longitudes
en los instantes t1, t2, respectivamente.
Si se trazan los valores de esta tasa de crecimiento en relación con
la longitud media 1/2(l1 + l2), se
obtendrá un gráfico correspondiente a la ecuación (3.1);
la intersección con el eje de las X dará una estimación
de L¥ y la pendiente
una estimación de -K.
,
en donde l1, l2 son las longitudes
en los instantes t1, t2, respectivamente.
Si se trazan los valores de esta tasa de crecimiento en relación con
la longitud media 1/2(l1 + l2), se
obtendrá un gráfico correspondiente a la ecuación (3.1);
la intersección con el eje de las X dará una estimación
de L¥ y la pendiente
una estimación de -K.
Con los datos de longitudes a intervalos iguales de tiempo T, se puede transformar la ecuación (3.2):
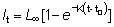
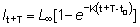
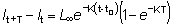
(3.3)
El gráfico de los incrementos lt+T - lt contra el largo inicial lt da, por lo tanto, una recta cuya pendiente será -(1 - e-Kt), y cuya traza en el eje de las X será L¥ (véase fíg. 4a). Un caso especial importante es T = 1 año, cuando la pendiente será = - (1 - e-K). Otra forma de la ecuación (3.3) será:
(3.4)
la cual, para T = 1 nos da el conocido gráfico de FORD-WALFORD, trazando lt+1 contra lt La pendiente de la recta es e-K, y la intersección con la bisectriz (donde lt+1 = lt), será una estimación de L¥ (véase fig. 3.1 b). Este gráfico es esencialmente el mismo que el obtenido con la representación gráfica de los incrementos (lt+1 - lt) contra la longitud inicial, lt. Los puntos se ajustarán mejor a la línea de FORD-WALFORD, pero debido a que la línea de regresión y la bisectriz forman un ángulo muy pequeño, L¥ es estimado con la misma precisión por ambos gráficos, y si el ajuste se hace gráficamente, en vez de hacerlo mediante el cálculo de las líneas de regresión (por ej., por mínimos cuadrados), se introducirán mayores errores en el trazado de lt+1 contra lt.
FIG. 3.1 Estimación de las constantes de crecimiento
a) Representación de los valores del incremento de la longitud respecto a la longitud inicial

b) Representación de la longitud respecto a la de un año antes
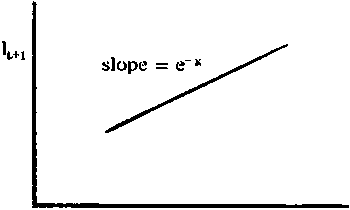
L¥ y K pueden ser determinados directamente a partir de las rectas ajustadas a estos gráficos, tanto por análisis de regresión como a mano alzada; entonces t0 puede estimarse a partir de la ecuación (3.2) para cualquier par de observaciones de longitudes y edades. Con este objeto, la ecuación (3.2) puede ser escrita en la forma:
o bien,
(3.5)
Aunque de esta forma puede ser obtenida una estimación de t0 para cada edad para la cual sea conocida la longitud media, estas estimaciones no serán todas igualmente buenas. Las estimaciones procedentes de peces viejos serán muy variables, debido a que una pequeña diferencia en lt da una gran diferencia en la estimación de t0 cuando lt es casi igual a L¥ . Las estimaciones a partir de los peces más jóvenes pueden estar sesgadas debido a que los peces de esas edades que aparecen en las capturas son los mayores. La mejor estimación de t0 sería la media de las estimaciones de t0 obtenidas de los grupos de edad más jóvenes, pero que están completamente reclutados.
Alternativamente, sólo L¥ es estimado a partir del gráfico de incrementos contra longitudes iniciales.
De éste puede calcularse
Partiendo de la ecuación (3.5) y trazando el gráfico de 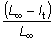 contra t se obtendrá una recta cuya pendiente será -K,
y cuya traza con el eje de las t será t0.
contra t se obtendrá una recta cuya pendiente será -K,
y cuya traza con el eje de las t será t0.
Los datos de longitudes a intervalos anuales pueden obtenerse y tabularse de varias formas. Probablemente la forma más directa es el análisis del crecimiento de un solo pez. La longitud al cabo de un año de vida puede obtenerse a partir de medidas de escamas, otolitos o cualquier otra estructura dura. En lugar de ello puede seguirse el crecimiento de una clase anual durante un período de años, por ejemplo, para la clase anual de 1956, el incremento en el quinto año de vida es la diferencia entre la longitud media de los peces de cinco años al final de 1961, y los peces de cuatro años al final de 1960. Ambos métodos están relacionados con el crecimiento de un grupo de peces durante su vida; y el crecimiento en cada año de vida dará un punto en el gráfico. De esta forma, los incrementos en el crecimiento serán los correspondientes a diferentes años; por ejemplo, para la clase anual de 1956, el incremento en el tercer año de vida será en 1959, posiblemente en condiciones muy diferentes a las de 1961, es decir, el quinto año de vida. El crecimiento durante un año determinado puede ser estudiado usando el crecimiento de clases anuales diferentes - por ejemplo, los datos sobre el crecimiento en 1960 vienen dados por el crecimiento de la clase anual de 1956 en su quinto año de vida -, cada clase anual da un punto en el gráfico. Este es un método particularmente útil para estudiar el efecto del medio - alimento, temperatura, densidad, etc., sobre el crecimiento -. Finalmente, el crecimiento puede estimarse a partir de los datos de un solo año, por ejemplo, de los datos de 1960 puede ser estimado el incremento en el quinto año de vida partiendo de la diferencia en longitud de las clases anuales de 1955 y 1956, el incremento en el cuarto año partiendo de la diferencia entre las clases anuales de 1956 y 1957, etc. Estas diferencias no corresponden realmente al crecimiento de un pez o grupo de peces en particular, y el método debe ser usado solamente cuando no puedan usarse otros. Mejor sería tomar el tamaño medio para cada edad a lo largo de un cierto número de años, pero en este caso es generalmente posible, y más satisfactorio, analizar el crecimiento de las clases distintas anuales individuales o en cada año civil.
En general, el peso de un pez es aproximadamente proporcional al cubo de su longitud, de manera que, de la ecuación (3.2), se obtendrá:
(3.6)
en la que W¥ es el peso asintótico, que corresponde al largo asintótico L¥
Análogamente, si el peso fuese proporcional a la potencia n de la longitud, la ecuación (3.6) sería:
Cuando los datos de crecimiento se dan en función del peso, el ajuste de las curvas de crecimiento es llevado a cabo con más facilidad usando la raíz cúbica del peso como un índice de la longitud, ajustando estos datos a ecuaciones de crecimiento en longitud como se hizo anteriormente, y finalmente elevando al cubo para volver a peso.
Una ecuación de crecimiento más general es la dada por RICHARDS; con un pequeño cambio en su notación resulta:
(3.7)
Para diferentes valores de m, esta ecuación se transforma en una u otra de las ecuaciones de crecimiento más comunes. De esta forma, si m = 2/3, la ecuación (3.7) se transforma en la misma ecuación de la curva de VON BERTALANFFY (2.5). Si m = 2, la ecuación, con ciertas modificaciones, se convierte en la ecuación autocatalítica:
y para m = 0, en la ecuación monomolecular
Wt = W¥ (1 - ae-Kt)
y puede demostrarse que en el límite, a medida que m ® 1, la ecuación se convierte en la de GOMPERTZ: log wt = log W¥ (1 -ae-Kt). Esta curva satisface una relación semejante a la de la ecuación (3.1), solamente en función del logaritmo de la longitud y no de la longitud, es decir:
Las expresiones anteriores dan el peso o la talla de un pez en función de su edad. A veces, se requiere la inversa, es decir, se desea saber la edad del pez de una determinada longitud, v.g., los datos de selección se dan normalmente en función de la longitud, pero para incorporarlos a las ecuaciones de rendimiento necesitan ser expresados en función de la edad.
Si la forma de crecimiento estacional tiene variaciones muy marcadas, y todos los peces de una determinada edad tienen aproximadamente la misma longitud, la edad media efectiva a que un pez alcanza un tamaño dado puede ser muy diferente de la edad media deducida de la curva de crecimiento medio anual, especialmente al principio y al final de la temporada de crecimiento rápido. Si así ocurre, la conversión de longitud a edad se realiza mejor empíricamente a partir de la curva observada de edad-longitud. Asimismo, y particularmente si existe mucha divergencia individual en el crecimiento, la curva de la talla media a una edad determinada será diferente de la curva de la edad media a una longitud determinada (lo mismo que, generalmente, la línea de regresión de y sobre x es diferente de la línea de regresión de x sobre y). Normalmente, sin embargo, es suficiente convertir la longitud a edad mediante una ecuación de crecimiento ajustada a todos los datos observados de longitudes medias a edades determinadas como, por ejemplo, la ecuación de VON BERTALANFFY
Para obtener t en función de 1, dividiremos ambos términos por L¥ y los restaremos de la unidad, lo que dará:
Tomando los logaritmos naturales de ambos términos tendremos:
y por lo tanto
(3.8)
Por consiguiente, el lapso de vida t2 - t1 entre dos tallas l1, l2 es
(3.9)
1. La ecuación de crecimiento de VON BERTALANFFY contiene tres parámetros (L¥ , K y t0) los cuales pueden ser estimados partiendo de tres observaciones de la longitud a determinadas edades. Partiendo de la ecuación (3.2) escríbanse las longitudes en los instantes t - 1, t, t + 1, y los incrementos en longitud entre t - 1 y t, y entre t y t + 1. Seguidamente, determínese una estimación de K partiendo de la razón entre estos incrementos; sustituyendo K por esta estimación en la ecuación (3.2), o en otra forma, hallar una estimación de L¥ en función de lt y de los incrementos.
2. KITASAMA y HITOSHI (1955) dan los siguientes datos de longitudes y edades para el arenque del Pacífico, Clupea pallasii C. y V., capturado en aguas de la costa occidental de Hokkaido entre 1910-1954. Las longitudes son promedios tomados durante un período de 45 años; las edades fueron determinadas a base de los anillos de las escamas.
|
Edad |
Longitud total |
|
3 |
25,70 |
|
4 |
28,40 |
|
5 |
30,15 |
|
6 |
31,65 |
|
7 |
32,85 |
|
8 |
33,65 |
|
9 |
34,44 |
|
10 |
34,97 |
|
11 |
35,56 |
|
12 |
36,03 |
|
13 |
35,93 |
|
14 |
37,04 |
|
15 |
37,70 |
|
W = 7,8 x 10-3 L3 gm |
|
a) Construir una planilla de trabajo y determinar L¥ , W¥ , K y t0.
b) Calcular las curvas teóricas de crecimiento en longitud y peso de 0 hasta 15 años.
3. YOKOTA da los datos siguientes del crecimiento del tiburón Mustelus kanekonis (edad determinada partiendo de los cambios estacionales en la longitud de los pterigopodios).
|
Grupos de edad |
Peso (g.) |
|
I |
375 |
|
II |
1,519 |
|
III |
2,430 |
|
IV |
3,247 |
|
W = 7,4 x 10-3 L3 gm |
|
a) Determinar L¥ , W¥ , K y un valor práctico para t0
b) Calcular las curvas de crecimiento en longitud y peso hasta el grupo de edad VIII.
4. POSGAY (1953) realizó el marcado de vieiras y obtuvo los datos siguientes sobre crecimiento durante los 10 meses (aproximadamente) entre la marcación y la recaptura.
|
|
Diámetro de la concha (mm.) | |||||||||
|
En el momento de la marcación... |
64 |
69 |
71 |
94 |
104 |
105 |
110 |
117 |
117 |
126 |
|
En el momento de la recaptura... |
98 |
102 |
93 |
115 |
120 |
126 |
125 |
127 |
136 |
138 |
a) Calcular L¥ y K.
b) Suponiendo t0 = 0, calcular y trazar la curva de crecimiento en longitud hasta los 6 años.
5. OCHIAI (1956) da los datos siguientes del crecimiento de los len guados Heteromycteris japonicus y Pardachirus pavoninus.
|
Edad |
Longitud «standard» |
|
|
H. japonicus |
P. pavoninus |
|
|
1 |
6,09 |
10,00 |
|
2 |
8,10 |
14,80 |
|
3 |
9,20 |
|
a) Determinar aritméticamente L¥ , K y t0, para cada especie (suponiendo t0, = 0 para P. pavoninus).
b) Obtener las expresiones del crecimiento en peso suponiendo una relación cúbica entre el peso y la longitud.
6. MOISEEV da los datos siguientes de crecimiento (longitud total en cm.) del lenguado Limanda aspera en la Bahía de Pedro el Grande (Mar del Japón):
|
Edad |
Sexo |
Año del muestro |
||||
|
1928 |
1930 |
1931 |
7932 |
7933 |
||
|
1 |
|
5,15 |
7,60 |
6,58 |
7,72 |
8,34 |
|
|
5.77 |
7,22 |
7,20 |
9,50 |
7,34 |
|
|
2 |
|
10,25 |
13,60 |
11,70 |
13,80 |
14,10 |
|
|
11,77 |
11,88 |
13,20 |
15,50 |
12,68 |
|
|
3 |
|
16,40 |
19,40 |
17,42 |
18,82 |
19,44 |
|
|
17,41 |
19,00 |
18,80 |
21,00 |
18,68 |
|
|
4 |
|
20,45 |
24,00 |
21,22 |
22,92 |
24,32 |
|
|
22,13 |
25,00 |
23,60 |
25,50 |
25,32 |
|
|
5 |
|
25,05 |
26,80 |
25,42 |
26,38 |
27,66 |
|
|
26,51 |
26,12 |
27,60 |
29,50 |
27,32 |
|
|
Indice de la captura demersal total |
1 |
1 |
5,5 |
8,0 |
7,7 |
|
a) Analizar las diferencias en el crecimiento según el sexo.b) Teniendo presente que la pesca en gran escala sólo se inició en la bahía en la temporada 1929-30, y que L. aspera constituía el 80 % de la captura de peces demersales, examinar las variaciones de crecimiento de año a año.
c) La composición media por edades en número de individuos, durante 1931-33, fue la siguiente:
|
Edad |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
% |
0,6 |
4.7 |
16,1 |
33,3 |
27,9 |
11,3 |
3,4 |
1,7 |
0,9 |
0,2 |
Estimar el coeficiente de mortalidad total y examinar los datos de crecimiento para ver el sesgo en la longitud media a cada edad, debido a la selección.
(Esta parte del ejercicio se efectuará después de las secciones 5 y 7.)