E.A. Gardner¹ K.J. Coughlan¹ and D.M. Silburn²
1. Soil Conservation Research Branch, Department of Primary Industries, GPO Box 46, Brisbane, Queensland 4001, Australia.2. Soil Conservation Research Branch, Department of Primary Industries, Tor St, Toowoomba, Queensland 4350, Australia.
Abstract
Introduction
Soil water content
Plant available water capacity
Infiltration
Evaporation
Drainage
Management practices
Conclusions
Acknowledgements
References
Measuring and interpreting profile soil water changes, infiltration and runoff under ponded and rainfall conditions, and evaporation and deep drainage in Vertisols, are discussed. Measurement of soil water parameters/processes in Vertisols is usually no more difficult than in rigid soils. However, there is more to be understood about rainfall infiltration into Vertisols, and its quantitative prediction.
Of the 50 million ha of Vertisols in Queensland, 1.2 million ha are used for dryland grain production in areas receiving less than 500 mm rainfall per year. Research at the Soil Conservation Research Branch of the Department of Primary Industries in Queensland is concentrated on stabilising grain yield, either by catchment water management practices or by matching cropping pattern to soil water supply and rainfall reliability, and on decreasing soil erosion and managing peak storm runoff rates from cropped areas.
Three techniques of soil water management are considered: fallowing, opportunity cropping and optimising crop-soil-climate combinations using modeling. The rainfall pattern in Queensland makes summer fallowing on Vertisols very inefficient because most of the rain is lost as evaporation (about 65%) and runoff (about 17%). Rather, opportunity cropping, using the rain as it falls, is better, but this approach is not economically successful in all cropping areas of Queensland. It is suggested that it is only through crop growth models that the interaction of soil water storage, climate, crop type and planting date on grain yield can be sensibly judged, using long-term (>80 years) simulations of crop yield from rainfall data, to incorporate the effects of a highly variable rainfall pattern. Results from such a model are presented.
Water supply to crops is the major constraint to grain yield on the 1.2 million ha of Vertisols used for dryland (and irrigated) cropping in Queensland. Dryland research concentrates on cropping strategies, such as matching planting date to soil water and rainfall reliability, with appropriate surface soil management strategies to increase soil water storage and reduce erosion. In irrigated areas, irrigation frequency, transient surface waterlogging and water quality in relation to profile permeability are studied. In both types of cropping environment, soil water parameters and processes such as soil evaporation and deep drainage must be measured. The unique characteristic of Vertisols is their volume change with changes in moisture content, which influences these soil water processes.
A convenient framework to consider soil water behaviour is the catchment water balance equation:
Infiltration = rainfall + irrigation - runoff
= change in soil water store
+ drainage below root zone
+ evaporation + transpiration.
Change in soil water content
Volumetric soil water content, q v (volume of water per unit volume of soil), is one of the fundamental descriptors of the water status of a soil. It is numerically equal to the depth of stored water per unit depth of soil. The gravimetric soil water content, q g, is expressed in terms of the weight of water per unit weight of soil. For a non-swelling field soil, the change in profile soil water content, D S, over a given time interval, may be calculated as:
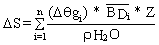units of cm or mm (1)
where:
Z = the depth of the sampling increment-usually 10 cm.
= the average bulk density of depth increment i
D q gi = the difference in gravimetric moisture content between any two sampling times for the i-th depth increment
n = the number of depth increments, each of length Z
r H2O = the density of water.
For swelling soils, there are a number of apparent difficulties in the application of equation l:
· variation in bulk density with water content; and· difficulty in measuring bulk density accurately on cracked soil, because the cracks must be representatively sampled.
However, Gardner (1978), Bridge and Ross (1984) and Yule (1984) have shown that because bulk density variations are exactly compensated by soil height changes, and because cracks are essentially closed at maximum field water content (q gmax), equation 1 can be used in swelling soils if the bulk density at q gmax is used:
(2)
where:
q gx = gravimetric water content at the indicated depth at time x
10 = the depth (cm) of the soil sampling interval at the reference wetness state.
The change in soil water storage is simply the difference in gravimetric water content between any two sampling occasions multiplied by the bulk density at the (fully wet) reference wetness state. The difficulties are in the measurement of bulk density.
Measurement of bulk density
Bulk density is:
where:
AD = the absolute density of the soil solids (about 2.65 g cm-3)
e = the volumetric concentration of soil air (cm³ cm-3).
For swelling soils our experience is that e at maximum field water content is approximately 0.05 cm³ cm-3. Hence, if q gmax is known, bulk density can be calculated. For example, 2 days after flood irrigation of a black earth soil in Queensland q g measured 0.5 g g-1. From equation 3, BDq gmax can be evaluated as 1.08 g cm-3.
If this gravimetric sampling and calculation procedure is repeated for a range of swelling soils in which q gmax varies (due to changes in clay content and/or mineralogy), pairs of BD (q gmax) and q gmax values can be plotted (Figure 1).
Figure 1. Relationship between field bulk density and maximum water content for a range of Vertisols in Queensland.
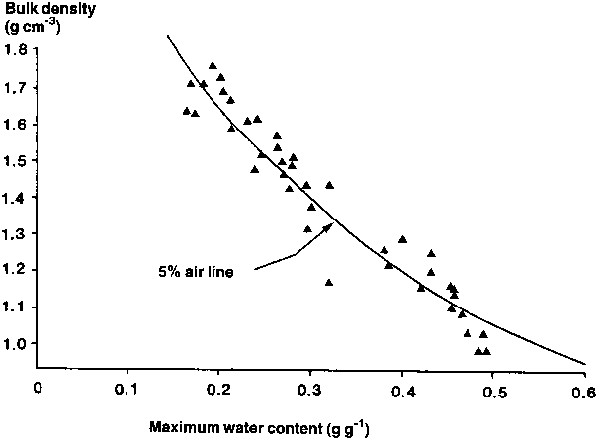
The effect of error in the assumed e values is not large. For example, if the true e = 0.10 cm³ cm-3, and assumed e = 0. 05 cm³ cm-3, then for q gmax = 0.50 g g-1, calculated bulk density reduces from 1.08 to 1.03 g cm-3. This is an error of less than 5%.
Equations 2 and 3 show that the calculation of soil water changes in Vertisols is almost as straightforward as that for rigid soils. Moreover, provided the soil profile is fully wet (de, at q gmax) the bulk density of a sample taken with a hand auger can be calculated using equation 3.
Low e values at q gmax infer a restricted aeration status of Vertisols in their fully wet state. An exception is the surface 10 em of irrigated raised beds (Yule et al, 1984).
Measurement of soil water using the gravimetric method
A fundamental problem in gravimetric sampling is that uncertainty in measurement (de, the variance) at each sampling occasion is additive when differences in q g are sought. The problem is partially resolved if the same locations can be monitored at each sampling occasion to take advantage of the reduction in error due to covariance.
Measuring soil water using the neutron moisture meter in Vertisols
The neutron moisture meter (NMM) is the obvious instrument to exploit the advantage of sampling at the same location. However, there are still errors arising from imprecision in the calibration equation (q v vs fractional count rate, Cf); instrument error in measuring a random radioactive process; and heterogeneous water distribution over sites, which is the major source of random error in any neutron meter measurement. Williams and Sinclair (1981) presented a comprehensive analysis of statistical errors associated with using an NMM. They stressed that the minimum variance associated with NMM use is set by the precision of the calibration equation. A highly precise field calibration equation is clearly important.
When using an NMM there are potential bias problems introduced by bulk density effects, bound water, slow neutron absorbers, high organic matter content and sharp water/soil or soil/air boundaries (Greacen et al, 1987). These apply both to Vertisols and rigid soils. In Vertisols, NM-M calibration poses special problems because bulk densities of dry, cracked soil are required, while the cracking pattern of the calibration bay must approximate that of the field. A simple method is to take large cores (100 mm diameter, 100 mm long) from an uncracked, fully wet soil profile (at q gmax) and monitor height and weight changes as the cores dry slowly in the laboratory (Yule and Ritchie, 1980). These data allow unique BD vs q g relationships to be established which are then applied to the field q g vs Cf data.
Alternatively, a mode of shrinkage can be assumed, such as three-dimensional, normal volume change, and bulk density at any q g is then calculated from an analytical expression given by Fox (1964). Failure to allow for shrinkage cracks in BD samplings/calculations can cause a negative bias of up to 30% in estimates of D q v, although a high precision in the calibration equation is still possible (Greacen and Hignett, 1979).
Shrinkage cracking inevitably occurs around the NMM access tube, but, provided the tube-air-soil-air-soil geometry is the same in the calibration bay as it is in the field plot, these geometry effects are 'calibrated out'. Preferential water movement down the crack formed between the access tube and the dry soil can occur, allowing infiltration through horizontal soil surfaces. This may cause pockets of dry soil to occur in the middle of the soil matrix between the shrinkage cracks. Consequently, q v estimated from an NMM calibration equation established on a drying soil may overestimate the true average q v in a wetting soil until the vertical wetting fronts link up.
Finally, when calculating profile moisture changes using an NMM, allowance must be made for the different profile heights (due to shrinkage) between any two sampling occasions. Failure to allow for this can introduce a relative error of 10-15% in the maximum AS (Gardner, 1985).
Plant available water capacity (PAWC) is a second fundamental soil hydrological parameter because:
· it sets the upper limit on the size of the plant soil water store;· it acts as the water supply buffer between rainfall events during crop growth; and
· it determines irrigation frequency, which influences water use efficiency, distribution canal capacity, and surface waterlogging.
Following Gardner et al (1984), PAWC can be defined as:
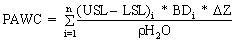(4)
where:
USL = the upper storage limit, the gravimetric water content of the wet soil after downward drainage is negligible.
LSL = the lower storage limit, the gravimetric water content after plant water extraction in the field.
RD = the rooting depth.
BD = the bulk density at the USL.
D Z = the depth interval considered.
r H2O = the density of water.
i = subscript referring to any one of n soil layers
PAWC may vary with crop, growth stage, stress level, root development restrictions, extent of soil water recharge, etc. but when measured using management appropriate for the intended application, it has proved an extremely useful concept for comparisons among soils (Straw and Yule, 1978; Gardner and Coughlan, 1982). We measured PAWC in the field using 25 m² mini-bays with an indicator crop and found that drainage becomes negligible 2-3 days after irrigation.
Hence, provided there is complete subsoil wetting, the USL is synonymous with q gmax. The LSL depends on soil depth and the level of drought stress we use to define the end of plant water extraction. In irrigated areas, this is visible plant stress for 2-3 consecutive days, while in dryland areas, it corresponds to the minimum q g measured during the crop cycle. Rooting depth varies with crop growth, the stress levels imposed, and between Vertisols: it is defined as the deepest soil depth of significant decrease in soil moisture between irrigations, or between wet and dry profiles in dryland crops.
Field determinations of PAWC on a wide range of Vertisols in Queensland have given values of 100-130 mm for mildly-stressed conditions to 70140 mm in severely-stressed sorghum. Differences in PAWC were caused mainly by differences in rooting depth (50-120 cm) between soils (Gardner and Coughlan, 1982; Shaw and Yule, 1978). Differences in the volumetric available water capacity (AWC) per unit soil depth had a second order effect with values ranging from 15-22 mm 100 mm-1.
Differing PAWC responses to extreme drying cycles have been observed in a number of irrigated Vertisols. The increased PAWC response to extreme drying cycles is caused by increased rooting depth and activity. An extreme example is a strongly self-mulching Typic Pellustert where the PAWC for mildly-stressed, irrigated sorghum is 120 mm, increasing to 290 mm for dryland ratoon sorghum with a stress level causing leaf death (Figure 2). For comparison, the AWC profile using the -15 bar q g as an estimate of the LSL is also shown. Summing the AWC profile over 150 cm soil depth gives 200 mm of available soil water. The soil properties allowing these rooting depth/activity-PAWC responses to plant stress are uncertain, but the response appears greatest in Vertisols with strong, very fine (<5 mm) to fine (5-10 mm) subangular, blocky soil structure with a well-developed, secondary structure of large (500 mm x 200 mm) lenticular peas. Subsoil aeration effects are hence strongly implicated.
In dryland experiments causing high plant stress levels, PAWCs of 200 mm in 180 cm of rooting depth are common in self-mulching clays, reducing to 120-130 mm in shallow soils (<80 cm) and in those Entic Chromusterts of low potential volume change and poor self-mulching ability. Methods of predicting USL, LSL, and RD from more easily-measured soil properties, such as -15 bar q g, are being studied.
Figure 2. Distribution with soil depth of the Available Water Capacity (AWC) and the Plant Available Water Capacity (PAWC) at two levels of plant stess for a Typic Pellustert.
Information on the infiltration process and rates is of importance in irrigation layout design, to assess likely waterlogging hazards, to understand the effects of surface management treatments on soil water accumulation, and for use in models which simulate the water balance using lengthy data sets (>80 years). Infiltration can be separated into ponded and rainfall conditions.
Ponded
The classic, buffered infiltrometer ring method to study ponded infiltration is a complete failure on Vertisols, because water in the inner ring moves away laterally into the interconnecting shrinkage crack network.
As an alternative, we built 25 m² mini-bays with a continuous, thin metal wall buried to about 120 cm, resulting in a water-tight, undisturbed, non-weighing lysimeter. The bays allowed a representative cracking pattern under row crop conditions to be sampled. Details on construction and measurement are given in Shaw and Yule (1978) and Gardner (1978). Infiltration was measured at different antecedent moisture contents by rapidly flooding the bay and thereafter maintaining fully-ponded conditions for 5-24 hours. In a wide range of Vertisols, two-thirds of the total net water addition was instantly taken by the soil to fill the crack volume. An example of this infiltration behaviour is shown in Figure 3, where cumulative infiltration is plotted as a function of the square root of elapsed pondage time. The Y axis intercept is the crack volume, while the slope of the line equals the sorptivity (S) (Philip, 1969).
Figure 3. Relationship between cumulative infiltration and the square root of time for a Typic Pellustert under ponded conditions for a range of antecedent soil water deficits.
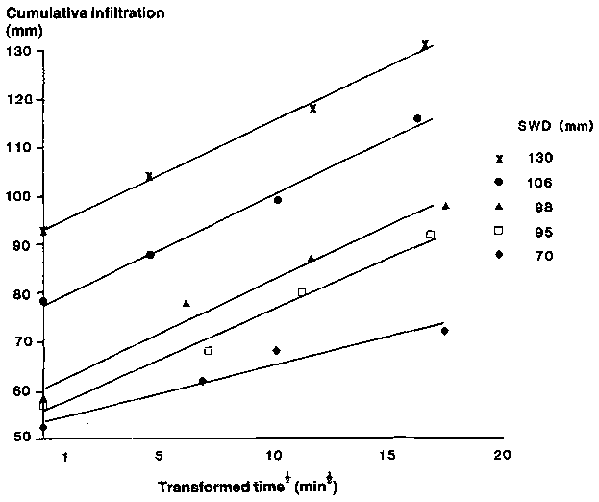
As the net water addition equated closely with the independently-measured initial soil water deficit (SWD), the cumulative infiltration (I) behaviour can be described by the equation:
I (t) = 2/3 * SWD + St0.5 (5)
where S varies with both antecedent soil water content and crack wall surface area (Gardner, 1978). Because the infiltration rate at the end of 5 hours was only to about 4 mm h-1, with a further reduction to about 1.5 mm h-1 after 24 hours of ponding, extended irrigation times added little water to these soils.
This variation in 'saturated' infiltration rate over time is consistent with saturated water flow through macrovoids, which swell shut slowly (Ritchie et al, 1972). Other studies on Vertisols in Queensland have established a 10-fold reduction in infiltration as ponding time increased from 24 hours to 7 days. This behaviour has implications for assessing the incidence of surface waterlogging and deep percolation under paddy rice (Gardner and Coughlan, 1982).
Rainfall
Measuring and describing infiltration behaviour under rainfall (a flux-controlled boundary condition) is much more difficult, requiring, among other things, the prediction of time to ponding as affected by variation in rainfall intensity and antecedent soil water deficits. Complications are caused by the formation of surface seals of large hydraulic resistance and layered soil hydraulic properties. Tilled Vertisols combine all these characteristics. Because of the above problems, attempts have been made to collect empirical infiltration data using rainfall simulators (McKay and Lock, 1978; Glanville, 1984).
Instrumented catchments can also be used to obtain information on rainfall infiltration on either a storm or short-time basis. A common difficulty with the latter approach is that the generation of excess rainfall rate (R) is not time-synchronised with the measured runoff rate (Q), because the depth of ponded water on the soil surface must continuously adjust to allow for varying rates of surface runoff. Only in a steady state condition does R = Q. Rose (1985) solved this problem for simple rectangular catchments. He showed, for specified times (t), how R (t) could be calculated from Q (t) data which, when combined with measured rainfall rate data, P (t), allowed infiltration rate, i (t), to be calculated:
i (t) = P (t) - R (t) (6)
The task of describing these experimental data by physically-based infiltration equations appropriate to Vertisols, which both crack and surface seal, remains unresolved.
The effect of summer fallowing on evaporation is of interest because data from southeast Queensland indicate that some 65% of fallow rainfall (of about 450 mm) is repartitioned into soil evaporation (Freebairn et al, 1986a). Evaporation rates also may be responsive to levels of surface cover (Bond and Willis, 1969) and tillage.
Weighing lysimeters 570 mm diameter x 400 mm long were used to evaluate evaporation losses in relation to surface cover and simulated tillage (Freebairn et al, 1986b). After 3 days there was little effect of stubble on evaporation from a repacked black earth (Figure 4). Assessing evaporation response to simulated tillage practices and soil compaction by planting press wheels presents some difficulty in these small experimental units. However, weighing is the only practical way to capture the short-term evaporation behaviour.
Figure 4. Relationship between cumulative evaporation and cumulative time for a Typic Pellustert under bare surface and stubble mulch (4 t ha-1) conditions. Data were obtained from small weighing lysimeters.
Drainage estimates below the root zone are important to 'close' the catchment water balance; to assess the effect of a cultural practice, such as irrigation for paddy rice raising the regional water table; and to determine the suitability of saline water for irrigation (Straw and Thorburn, 1985a).
Drainage can be measured directly or by inference from analyses of tracers. Direct measurement can be of two types:
· measurement of changes in profile water content; or· calculation of flux rates using the measured soil hydraulic gradient (by tensiometers) and knowledge of the relationship between unsaturated hydraulic conductivity (K), and volumetric water content (q v).
The first method can be used only when the 'wetting front' is above the maximum depth of measurement, while the second method, often called the flux-gradient technique, is difficult to maintain for extended periods of time. Additional difficulty occurs in Vertisols because the maximum drainage rate, Ks, is small while the amount of water stored above field capacity is usually less than 0.02 cm³ cm-3 (Hodnett and Bell, 1981).
Because recharge in Vertisols is episodic, isotopic tracer techniques, which integrate long-term drainage behaviour, are an option. Despite their success (Allison and Hughes, 1978), the measurements are time-consuming and expensive.
An alternative tracer is the salt introduced by rainfall (Eriksson and Khunakasem, 1969), because under equilibrium conditions, salt flux into a soil equals salt flux out. By definition, salt flux equals a solute concentration (measured by electrical conductivity, EC) multiplied by a depth of water (either average yearly infiltration, I, or drainage, D). By assuming I equal to average yearly rainfall, Pg, Shaw and Thorburn (1985b) were able to establish a set of regression equations of the form:
(7)
where:
LF = leaching fractionr = rainfall
s = a soil depth below the active root zone
ESP = exchangeable sodium percentage of the soil (at 90 cm)
a,b,c = regression coefficients.
Shaw and Thorburn (1985b) tested the validity of their predictions by comparing predicted LF (from equation 7) with measured LF of Vertisols in three irrigation areas. Measured LF values varied from 0.01 (drainage = 1% of water applied) to 0.3, and agreement was good.
Background
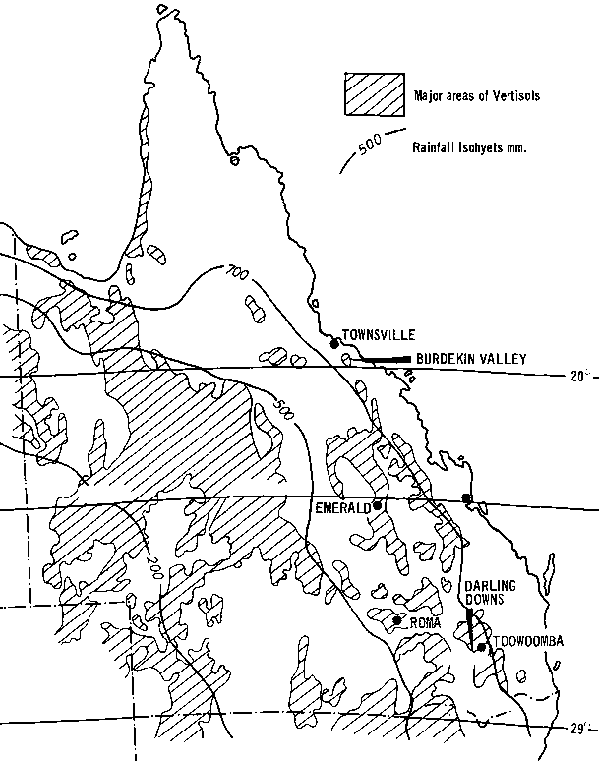
Cropping on Vertisols in Queensland for wet-land grain production occupies 1.5 million ha in the 500-700 mm rainfall zone (Figure 5). Soil water is a major constraint and farmers have responded by growing one crop per year and fallow for water storage during the other season.
Figure 5. Map of Queensland showing the distribution of Vertisols and mean annual rainfall isohyets.
Water management methods in dryland cropping have one or more of the following objectives:
· increasing fallow moisture accumulation by decreasing soil evaporation and storm runoff;· using rain when it falls by opportunity cropping irrespective of season;
· matching cropping strategies to PAWC and climate.
Fallow moisture storage
The major methods used to manipulate fallow moisture accumulation are tillage and crop residue management practices. Results from tillage-surface cover trials in Queensland have shown that the AS response is variable. The summer fallow moisture efficiency (D S divided by fallow rainfall) for a southeast Queensland area over a 5-year period averages only 20-25% (Wildermuth et al, 1986). Through stubble mulch and tillage, reduced runoff was found to improve the moisture storage from 18 to 24% but the tillage and crop residue management had no effect on evaporation, with 65 and 66% evaporation from bare fallow and stubble mulch/zero tilled plots, respectively (Freebairn et al, 1986). The reasons for such high evaporative losses are a combination of relatively small storms (20-80 mm), storms spaced at intervals of several weeks, and the relatively large amount of water (30-40 mm) held between air dry and q gmax in the surface 10-15 cm of Vertisols. Thus, soil water deficits (SWD) due to evaporation often approximate storm size, and it is only when average yearly rainfall is greater than soil water deficit that 'excess' water is available for subsoil recharge, as in central Queensland, where substantial moisture accumulation only occurs if storm sizes are >30 mm (Table 1).
Table 1. Soil water accumulation during fallows as related to rainfall amount and storm size at Emerald, central Queensland.
|
Stubble |
Date |
Soil water deficit (mm) |
Soil water change (mm) |
Total rain (mm) |
Rainfall >30 mm (mm) |
|
Wheat |
29.2.84 |
105 |
|
|
|
|
|
21.6.84 |
112 |
-7 |
80 |
Nil |
|
Wheat |
21.6.84 |
112 |
|
|
|
|
|
8.8.84 |
37 |
+75 |
123 |
75,38 |
|
Sunflower |
28.6.84 |
161 |
|
|
|
|
|
25.1.85 |
78 |
+83 |
310 |
75,45,39 |
|
|
|
|
|
|
37,38 |
|
Sunflower |
25.1.85 |
78 |
|
|
|
|
|
2.5.85 |
67 |
+11 |
126 |
Nil |
Source: Shaw and Thorburn (1985b).
Because evaporation is not easily modified by the stubble levels that we can generate (about 4 t ha-1), positive AS responses can most likely be achieved by reducing fallow runoff. However, average annual runoff from a Typic Pellustert for a bare fallow with stubble burnt was reported to be only 89 mm from 780 mm of annual rainfall, most of which occurred in the summer fallow (Freebairn et al, 1986a). Stubble mulch reduced runoff by 30 mm, but although much of this 30 mm difference is repartitioned into D S, the effect on wheat yield was small (<200 kg ha-1).
One possible reason for difficulties in reducing runoff is that, unlike the monsoons of India and parts of Africa, rain during the Queensland summer falls in small (<70 mm), well-spaced storms, which allows the shrinkage cracks to swell shut near the surface. Consequently, during the latter half of the fallow, much of the rainfall must infiltrate vertically through the soil matrix, and it is under these conditions that runoff responses to surface cover and surface roughness are observed (Freebairn and Wockner, 1986). Surface cover serves an important secondary role in reducing peak storm runoff rates, which has obvious implications to the design ratings of hydraulic structures. Figure 6, taken from Freebairn et al (1986c), shows an example of this response.
Opportunity cropping
Opportunity cropping is defined as planting a crop whenever surface moisture conditions are satisfactory for seedling emergence, provided the soil profile moisture store equals or exceeds some specified fraction of PAWC (for example, water store >0.2 PAWC). The rationale behind this approach is to redirect evaporation from fallow land into biomass-producing transpiration. Depending on the amount and reliability of rainfall, this strategy involves either winter or summer or double cropping each year.
Source: Freebairn et al (1986c).
The success and adoption of this approach depends on soil type, amount and variability of summer rainfall, and average grain yields from the winter crop. Results from eastern areas of southeast Queensland (Freebairn et al, 1986c) indicate that double cropping (summer sorghum-winter wheat) has a small effect on annual runoff and erosion, but an additional 2 t ha-1 of grain is produced each year. The practice is not widely used by farmers because high average wheat yields (3 t ha-1) remove the economic urgency of accepting the management inconvenience of two crops per year.
Similarly, double cropping is not often used in western areas of southeast Queensland (for example, in Roma) because unreliable summer rainfall, relatively small PAWC (about 130 mm), and high evaporation rates combine to make summer cropping unacceptably risky (Berndt and White, 1976; Lloyd and Hamilton, 1984). Rather, it is better to fallow the land during the summer in order to maximise soil water store for the winter wheat crop, which averages 1.6 t ha-1.
Opportunity cropping is practiced in central Queensland (for example, in Emerald) with grain crops planted from December to May and again from August to September. The success of this cropping system in Emerald compared with Roma may be due to more summer rain (445 mm vs 360 mm), a smaller spacing between summer storms (de, PAWC buffer is not emptied before rain), and a smaller incidence of winter frosts which increases the flexibility of wheat planting dates. Time to flowering is an important determinant of wheat yield, because the timing of drought stress and frost hazard combinations can cause a variation from 0.8 to 2.0 t ha-1 in simulated wheat yield for identical planting soil moisture conditions (Woodruff, 1985).
Matching cropping to PAWC and climate
The cropping strategies used in the different climatic zones of Queensland have evolved by a process of trial and error. This is usually a very expensive learning process. To better understand how soils and climate interact to affect grain yield (and erosion) we are developing cropping models, initially for wheat, which explore the effect of PAWC, rainfall, planting profile water content, plant variety and frost hazard on the probability distribution of grain yield. There are two aspects to PAWC-climate-yield analysis: the probability of achieving high yields and the chances of avoiding low yields resulting in a monetary loss (de, risk aversion).
A simple form of this analysis is shown in Figure 7 where simulated wheat yield probabilities for two locations in Queensland are compared for two PAWC values. Wheat variety and planting date were held constant. A rainfall record of 80 years was considered.
For a PAWC of 100 mm, the median yield (yield at 50% probability of exceedence) at Greenmount (eastern southeast Queensland) was 1600 kg ha-1 compared with 1300 kg ha-1 for Roma (western southeast Queensland). The yield difference is not large although median growing season rainfall was 250 mm and 195 mm, respectively. However, if PAWC is 200 mm, median wheat at Greenmount increases dramatically to 2400 kg ha-1, while at Roma the increased yield is only 1600 kg ha-1. The reason is that the probability of actually filling the 200 mm PAWC profile at Roma during a summer fallow is much less than at Greenmount. Median profile water stores at planting were 180 and 135 mm (data not shown). Thus soils with large PAWC may confer only a small yield advantage in dry areas because they are rarely filled to capacity. Similarly, in areas (or years) of high growing-season rainfall, large PAWC values will also confer little yield advantage.
Figure 7. Probability distribution of simulated wheat yields on a Typic Pellustert for two Plant Available Water Capacity (PAWC) values (100 mm and 200 mm) at two locations in southeast Queensland. Period used in the simulation was 80 years. Average annual rainfalls are 571 mm (Rome) and 735 mm (Greenmount).
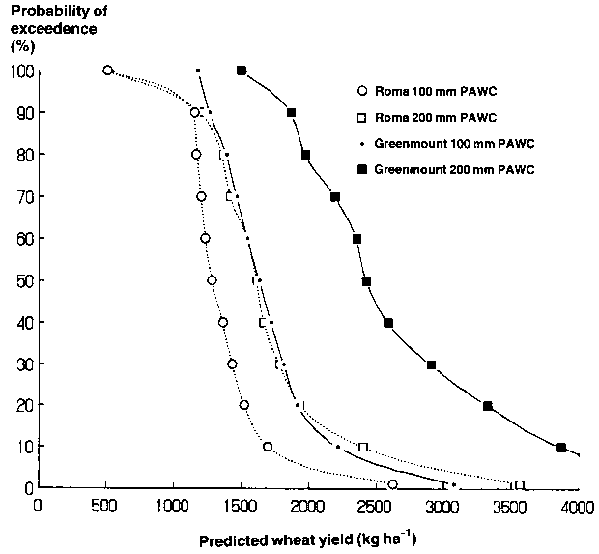
Figure 7 may also be used to determine risk aversion. Assuming the wheat yield to break even is 1400 kg ha-1, this may be achieved 80% of the time at Roma for a PAWC of 200 mm. The converse is that, in 1 year out of 5, the farmer will make a loss. However, if PAWC equals 100 mm, this risk increases to 6 years in 10. Clearly, large PAWC values are an advantage in reducing the risk of monetary loss in low rainfall areas. At Greenmount, the probability of losing money is negligible because the Typic Pellusterts there have PAWCs >200 mm (Freebairn et al, 1986a).
These simulated wheat yields are dominated by the relative transpiration rate at or near anthesis, which can be reduced by small leaf area and/or a low soil water store at this time (Woodruff and Tonks, 1983). In contrast, pasture has no yield-sensitive growth stages. Consequently, large differences in PAWC have much less influence on simulated yield (McCown, 1973).
Measuring and predicting the components of the catchment water balance is not an easy task for any type of soil or cropping system. The measurement of soil water parameters and processes in Vertisols is generally not much more difficult than in rigid soils. However, to make sensible comments on the long-term consequences of adopting various surface management treatments and cropping systems in a climate with highly variable (both in time and space) rainfall patterns, physically-based simulation models are required.
These models require both a sound physical understanding of how hydrological processes respond to management treatments, and the expression of this understanding by quantitative equations. The level of understanding of rainfall infiltration into Vertisols in the Queensland context is inadequate.
Similarly, a better understanding of why relatively subtle differences in climate and soil cause the success or failure of opportunity cropping techniques is necessary. It is likely that this understanding will require, in part, a closer examination of the soil physics of the upper 20 cm of the soil profile, since the water balance of this layer determines opportunities to plant crops, which, in turn, strongly influence the probability of drought stress at flowering (and, hence, crop yield).
Although a large PAWC does not ensure high crop yields unless sufficient fallow and growing season rain occurs, its value is still an important variable in any cropping model. There is a need to understand those soil properties which allow (or prevent) deep and active subsoil rooting, which overwhelming determines PAWC in Vertisols.
It is with great pleasure that we thank our colleague Roger Shaw for his editorial surgery on the manuscript, Alan Geritz for drafting the figures, Mark Littleboy for computing support, and Sandy Dunne for the word processing.
Allison G B and Hughes M W. 1978. The use of environmental chloride and tritium to estimate total recharge to an unconfined aquifer. Australian Journal of Soil Research 16:181-195.
Berndt R D and White B J. 1976. A simulation-based evaluation of three cropping systems on cracking-clay soils in a summer rainfall environment. Agricultural Meteorology 16:211-229.
Bond J J and Willis W 0. 1969. Soil water evaporation: surface residue rate and placement effects. Soil Science Society of America Proceedings 33:445-448.
Bridge B J and Ross P J. 1984. Relations among physical properties of cracking clay soils. In: J McGarity, E A Hoult and H B So (eds), Properties and utilization of cracking clay soils. Reviews in Rural Science No. 5. University of New England, Armidale, NSW, Australia. pp. 97-104.
Eriksson E and Khunakasem V. 1969. Chloride concentration in groundwater, recharge rate and rate of deposition of chloride in the Israel coastal plain. Journal of Hydrology 7:178-197.
Fox W E. 1964. A study of bulk density and water in a swelling soil. Soil Science 98:307-16.
Freebairn D M and Wockner G H. 1986. A study of soil erosion on Vertisols of the eastern Darling Downs, Queensland. I. Effects of surface conditions on soil movement within contour bay catchments. Australian Journal of Soil Research 24:135-158.
Freebairn D M, Ward L D, Clarke A L and Smith G D. 1986a. Research and development of reduced tillage systems for Vertisols in Queensland, Australia. Soil and Tillage Research 8:211229.
Freebairn D M, Hancock N H and Lott S C. 1986b. Soil evaporation studies using shallow weighing lysimeters: techniques and preliminary results. In: Conference on Agricultural Engineering, Adelaide 1986, Institute of Engineers, Australia, National Conference Publication 86/3.
Freebairn D M, Wockner G H and Silburn D M. 1986c. Effect of catchment management on runoff, water quality and yield potential from Vertisols. Agricultural Water Management 12:1-19.
Gardner E A. 1978. Techniques for evaluating suitability for irrigation of cracking clay soils in the Emerald Irrigation Area. Master of Agricultural Science thesis, University of Queensland, Brisbane, Australia.
Gardner E A. 1985. Soil water. In: Identification of soils and interpretation of soil data. Australian Society of Soil Science Inc. Queensland Branch, Brisbane, Queensland, Australia. pp. 197-235.
Gardner E A and Coughlan K J. 1982. Physical factors determining soil suitability for irrigated crop production in the Burdekin-Elliot River area. QDPI (Queensland Department of Primary Industries) Agricultural Chemicals Branch Technical Report No. 20, Brisbane, Australia.
Gardner E A, Shaw R J. Smith G D and Coughlan K J. 1984. Plant available water capacity: concept, measurement and prediction. In: J McGarity, E H Hoult and H B So (eds), Properties and utilization of cracking clay soils. Reviews in Rural Science No. 5. University of New England, Armidale, NSW, Australia. pp.164-175.
Glanville S F. 1984. Rotating disc rainfall simulator. Soil Erosion Research Techniques Workshop. QDPI (Queensland Department of Primary Industries) Conference and Workshop Series QC 84001:10-18.
Greacen E L and Hignett C T. 1979. Sources of bias in the field calibration of a neutron meter in a cracking clay. Australian Journal of Soil Research 17:405-415.
Greacen E L, Correll R L, Cunningham R B. Johns G G and Nicolls K D. 1987. Calibration. In: E L Greacen (ed.), Soil water assessment by the neutron method. CSIRO (Commonwealth Scientific and Industrial Research Organisation), Australia. pp. 50-81.
Hodnett M G and Bell J P. 1981. Soil physical processes of groundwater recharge through Indian black cotton soils. Institute of Hydrology Report No. 77. Wallingford, UK.
Lloyd P L and Hamilton N A. 1984. Climatic influence on agriculture. In: D A K McNee (ed.), Cropping in the Maranoa and Warrego, QDPI (Queensland Department of Primary Industries) Information Series QI84012:1-15.
McCown R L. 1973. An evaluation of the influence of available soil water storage capacity on the growing season length and yield of tropical pastures using simple water balance models. Agricultural Meteorology 11:53-63.
McKay M E and Loch R J. 1978. A modified Meyer rainfall simulator. Institute of Engineering, Australian Conference on Agricultural Engineering, Toowoomba. pp. 78-81.
Philip J R. 1969. Theory of infiltration. Advances in Hydroscience 5:215-296.
Ritchie J T. Kissel D E and Burnett E. 1972. Water movement in undisturbed swelling clay soil. Soil Science Society of America Proceedings 36:874-879.
Rose C W. 1985. Developments in soil erosion and deposition models. Advances in Soil Science 2:2-63.
Shaw R J and Thorburn P J. 1985a. Towards a quantitative assessment of water quality for irrigation. In: Planning and management of water for agriculture in the tropics. Fifth Afro-Asian Regional Conference, Townsville, Australia. ICID (International Commission on Irrigation and Drainage). pp. 41-52.
Shaw R J and Thorburn P J. 1985b. Prediction of leaching fraction from soil properties, irrigation water and rainfall. Irrigation Science 6:73-83.
Shaw R J and Yule D F. 1978. The assessment of soils for irrigation, Emerald, Queensland. Technical Report ho. 13. Agricultural Chemistry Branch, Department of Primary Industries, Brisbane, Australia. 84 pp.
Wildermuth G B Freebairn D M and McNamara R B. 1986. Influence of tillage on crown rot of wheat. Biennial Report 1982-84. Queensland Wheat Research Institute, Toowoomba, Australia.
Williams J and Sinclair D F. 1981. Accuracy, bias, and precision. In: E L Greacen (ed.), Soil water assessment by the neutron method. CSIRO (Commonwealth Scientific and Industrial Research Organisation), Australia. pp. 35-50.
Woodruff D R. 1985. Application of models to farm decision making. In: D A Charles-Edwards, J R Childs, J G Dingle, M A Foale, R J Hampson and S J Hill (eds), Application of computer models in farm management extension and research. Australian Institute of Agricultural Science, Brisbane, Australia.
Woodruff D R and Tonks J. 1983. Relationship between time of anthesis and grain yield of wheat genotypes with differing genotype patterns. Australian Journal of Agricultural Research 34:1-11.
Yule D F. 1984. Volumetric calculations in cracking clay soils. In: J McGarity, E Hoult and H B So (eds), Properties and utilization of cracking clay soils. Reviews in Rural Science No. 5. University of New England, Armidale, NSW, Australia. pp.136-140.
Yule D F and Ritchie J T. 1980. Soil shrinkage relationships of Texas Vertisols I. Small cores. Journal of the Soil Science Society of America 44:1285-1291.
Yule D F. Keefer G D, Ladewig J H and Nickson D J. 1984. Irrigation management studies with cotton on cracking clay soils at Emerald. In: W A Muirhead and E Humphreys (eds), Root zone limitations to crop production on clay soils. Symposium of Australian Society of Soil Science, Riverina Branch, Griffith, NSW, Australia. pp. 249-257.
