7.1 Rentabilité d'une affaire
7.2 Diagramme de flux de trésorerie
7.3 Méthodes d'estimation de la rentabilité
7.4 Considération de risques
7.5 Avantages et inconvénients des différentes méthodes d'estimation de la rentabilité
7.6 Analyse de rentabilité
7.7 Rentabilité des pêcheries artisanales
7.8 Rentabilité d'usines de transformation de poissons de petite et moyenne dimensions
7.9 L'inflation dans le calcul de rentabilité
"La rentabilité" est un terme général qui mesure le revenu qui peut être obtenu dans une situation particulière. C'est le facteur commun de toutes les activités de production. Certains paramètres doivent être introduits afin de définir la rentabilité. Le bénéfice brut (BB) pour la société est égal au revenu des ventes totales (V) diminué des coûts de production totaux sans amortissement (C), comme suit:
BB = V - C.........(7.1)
Lorsque l'on considère les coûts de dépréciation, le bénéfice brut avant impôt (BBAI) est le résultat de l'opération:
BBAI = BB - e × IF = V - C - e × IF.........(7.2)
dans laquelle: e = facteur de dépréciation interne.
Des taxes sont imposées sur ces revenus bruts, ce qui fait que l'investisseur ne reçoit pas la totalité de l'argent. Elles représentent un facteur important lorsque l'on évalue l'aspect économique des mesures alternatives. Le taux d'imposition diffère selon le pays, par exemple (source: Institut Français du Pétrole, 198l):
|
Pays |
Pourcentage |
|
USA |
52 |
|
Canada |
41 |
|
Allemagne |
51 |
|
France |
50 |
|
Italie |
35 |
|
UK |
53,75 |
|
Japon |
50 |
Par exemple, le taux d'imposition en 1980 aux USA a été appliqué de la manière suivante (Jelen et Black, 1983):
|
|
Pourcentage |
|
Taux sur les premiers $EU 25 000 gagnés: |
17 |
|
Taux sur les $EU 25 000 suivants gagnés: |
20 |
|
Taux sur les $EU 25 000 suivants gagnés: |
30 |
|
Taux sur les $EU 25 000 suivants gagnés: |
40 |
|
Taux sur les revenus supérieurs à $EU 100 000: |
46 |
Le même type de situation peut se rencontrer dans les pays en de développement. Par exemple, en 1969, le Pérou utilisait l'échelle d'imposition suivante (Engstrom et al., 1974):
|
|
Pourcentage |
|
Pour les revenus inférieurs à $EU 2 326 |
20 |
|
Revenus compris entre $EU 2 326 et 11 628 |
30 |
|
Revenus supérieurs à $EU 11 628 |
35 |
Il est à noter que les niveaux d'imposition et les procédures changent fréquemment dans certains pays (par exemple chaque année). Lorsqu'il n'est pas possible de déterminer la taxe exacte, une taxe arbitraire de 40-50% sur le bénéfice net avant impôt est suggérée. Le bénéfice net (BN) peut être calculé de la manière suivante:
BN = V - C - e × IF - t (S - C - d × IF) .........(7.3)
où: d = facteur officiel de dépréciation et t = taux d'imposition.
Le passage de l'argent dans ou hors de l'entreprise est appelé flux de trésorerie FT et est défini par la différence entre le revenu et les coûts de fonctionnement, en excluant la dépréciation et après le paiement des taxes; on peut donc l'exprimer comme suit:
FT = BN + e × IF = V - C - t × (V - C - d × IF) = BB - t × (V - C - d × IF) .........(7.4)
Le flux de trésorerie ou le bénéfice net ne sont pas une mesure de la rentabilité mais ils sont utilisés pour calculer la rentabilité d'un projet particulier. L'objectif d'un investisseur ou d'une société est toujours d'optimiser les gains par rapport aux coûts du capital à investir. Si l'objectif était seulement de maximaliser les gains, tout investissement pouvant générer des profits serait acceptable, en dépit de revenus faibles ou de coûts élevés.
Dans les études économiques où différentes alternatives pour un projet doivent être comparées, ou lorsqu'une comparaison doit être faite entre la rentabilité d'un projet et la profitabilité des transactions financières existantes, les méthodes d'analyse utilisées permettent d'effectuer cette estimation sur une base uniforme.
Tous les projets d'investissement indiquent une action qui va se développer sur plusieurs années dans le futur. L'étude des caractéristiques financières d'un projet nécessite l'analyse de la valeur temps de l'argent, du risque financier, des variations futures des prix de vente, des coûts, du volume des ventes et des taux d'imposition, du temps nécessaire pour réaliser le projet ou installer l'équipement avant de commencer la production normale et la vie économique du projet. Ces facteurs sont les suivants:
IF = Investissement fixe initial amortissable
Iw = Fonds de roulement
IR = Investissement résiduel = Terrain + Iw
A = Gains annuels
B = Production annuelle de liquidités à partir de la dépréciation
C = Période de construction
Une façon de visualiser nombre de ces facteurs est d'utiliser un digramme de flux de trésorerie comme indiqué à la Figure 7.1 (Perry et Chilton, 1973).
Sur la Figure 7.1, l'argent est représenté sur l'axe des y et le temps sur l'axe des x. Le temps zéro est le point auquel l'usine commence à produire. Dans les situations négatives, le seul flux de trésorerie est négatif, étant donné qu'il représente l'argent payé pour le terrain et les investissements fixes, IF. Lorsque le procédé est prêt pour commencer, il faut considérer un supplément d'argent dans le fonds de roulement, IW. Lorsque le procédé commence à produire, l'argent entre dans le projet comme produit des ventes, V. Le flux de trésorerie s'accumule, passant du négatif au positif, et lorsque le projet est terminé, le capital investi dans l'actif circulant et le terrain est récupéré, résultant en un flux de trésorerie final positif.
Figure 7.1 Flux de trésorerie cumulatif pour un projet
Ce diagramme présente l'avantage de montrer toutes les caractéristiques financières, à l'exception du risque, la vitesse à laquelle le projet crée des richesses et les gains pour le réinvestissement.
Les plans financiers peuvent être présentés simplement en intégrant toutes les données en un «tableau ressources-emploi des fonds». Ces relevés montrent l'origine ou la source des fonds ainsi que leur destination finale.
Exemple 7.1 Tableau ressources-emploi des fonds
Préparez un tableau ressources-emploi des fonds pour l'usine de merlu congelé de l'exemple 2.1.
Données
IF = $EU 600 000 (Exemple 3.1)
IW = $EU 60 000 (Exemple 3.1)
Production quotidienne = 2 tonnes BF
Nombre de jours de travail par an = 270
N = 10 ans
Prix de vente = $EU 1 560/tonne BF
Coût de production unitaire = $EU 1 272/tonne BF (Exemple 4)
Réponse:
Ventes annuelles
= Production annuelle (tonnes BF/an) × prix de vente ($EU/tonne BF)
= 2 tonnes BF/jour × 270 jours/an × 1 560 $EU/tonne BF =
= 540 tonnes BF/an × 1 560 $EU/tonne BF = 842 400 $EU/an
Coût de production annuel = production annuelle (tonnes BF/an) × coût de production unitaire ($EU/tonne BF) = 540 tonnes BF/an × 1 272 $EU/tonne BF = 686 880 $EU/tonne BF
On utilise la méthode d'amortissement linéaire. Les résultats sont présentés dans le Tableau 7.1.
Tableau 7.1 Tableau ressources-emploi des fonds pour une unité de transformation des produits de la pêche (en $EU'000)
|
Activité |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|
Ressource | ||||||||||
|
Fonds propres |
480 |
|
|
|
|
|
|
|
|
|
|
Crédit bancaire (*) |
180 |
|
|
|
|
|
|
|
|
|
|
Ventes nettes de l'activité |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
|
Total (a) |
1 502 |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
|
Applications | ||||||||||
|
Investissement fixe |
600 |
|
|
|
|
|
|
|
|
|
|
Fonds de roulement |
60 |
|
|
|
|
|
|
|
|
|
|
Coûts de financement (**) |
27 |
|
|
|
|
|
|
|
|
|
|
Coûts de production |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
|
Total (b) |
1 374 |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
|
(a) - (b) |
129 |
156 |
156 |
156 |
156 |
156 |
156 |
156 |
156 |
156 |
|
Bénéfice net (***) |
77 |
93 |
93 |
93 |
93 |
93 |
93 |
93 |
93 |
93 |
|
Plus amortissement |
60 |
60 |
60 |
60 |
60 |
60 |
60 |
60 |
60 |
60 |
|
Flux de trésorerie |
137 |
153 |
153 |
153 |
153 |
153 |
153 |
153 |
153 |
153 |
Notes:
(*) Il existe un crédit bancaire, 30% IF = $EU 180 000. (**) Taux de crédit de la banque 15% annuel. Pour plus de simplicité on n'a considéré qu'une seule année de crédit. (***) Impôts à déduire des gains (40%).
7.3.1 Taux de rentabilité
7.3.2 Valeur actualisée (VA)
7.3.3 Taux d'intérêt actualisé (DCFRR, Discounted cash flow rate of return)
7.3.4 Durée de retour sur investissement (nr)
Les méthodes les plus courantes d'évaluation de la rentabilité sont les suivantes:
- Taux de rentabilité de l'investissement initial (iROI).
- Taux de rentabilité de l'investissement moyen (iRAI).
- Valeur actualisée (VA)
- Taux de rentabilité interne ®
- Temps de retour sur investissement (nR)
Dans les études d'ingénierie, le taux de rentabilité d'un investissement est exprimé normalement en pourcentage. La rentabilité annuelle divisée par l'investissement initial total représente la fraction qui, une fois multipliée par 100, représente le pourcentage de rentabilité de l'investissement. La procédure habituelle est de trouver la rentabilité sur l'investissement total initial, avec la valeur du bénéfice net moyen comme numérateur:
et ainsi, le taux de rentabilité de l'investissement initial (iRIO), sera:
Du fait de la dépréciation de l'équipement pendant sa vie utile, il est habituel de relier le taux de rentabilité à l'investissement moyen pendant la vie utile du projet. L'investissement moyen (Im) est déterminé comme suit:
où Vc = valeur comptable à l'année k.
On peut également utiliser une formule approximative pour calculer l'investissement moyen:
Im = IF/2.........(7.8)
Le taux de rentabilité de l'investissement moyen (iRAI) peut être déterminé avec l'équation suivante:
La méthode pour calculer le taux de rentabilité de l'investissement initial (iROI) est également connue comme méthode d'ingénierie, tandis que la méthode qui calcule le taux de rendement de l'investissement moyen (iRAI) est la méthode préférée des comptables.
Ces méthodes donnent des «valeurs points» qui sont applicables à une année particulière pour une année «moyenne» choisie. Il n'est pas tenu compte de l'inflation ou de la valeur temps de l'argent.
Exemple 7.2 Calcul du taux de rentabilité de l'investissement initial (iROI)
Calculez le taux de rentabilité de l'investissement initial pour l'usine de merlu congelé de l'exemple 7.1.
Réponse: Dans ce cas, lorsque les flux de trésorerie ne sont pas constants, il faut calculer les éléments suivants:
Bénéfice annuel net = flux de trésorerie annuel - coût d'amortissement annuel.........(7.10)
Les valeurs obtenues sont indiquées au Tableau 7.2
Tableau 7.2 Calcul du bénéfice annuel net pour l'usine du Tableau 7.1
|
Année |
Bénéfice annuel moyen ($EU) |
|
1 |
77 000 |
|
2 |
93 000 |
|
3 |
93 000 |
|
4 |
93 000 |
|
5 |
93 000 |
|
6 |
93 000 |
|
7 |
93 000 |
|
8 |
93 000 |
|
9 |
93 000 |
|
10 |
93 000 |
|
Total |
9 1400 ÷10 = 9 140 |
Le taux de rendement moyen de l'investissement initial sera:
(9 140 ÷ 660 000) × 100 = 13,8% par an
La valeur temps de l'argent n'est pas prise en compte étant donné qu'on utilise seulement le bénéfice moyen, pas son développement dans le temps. Les bénéfices des années 1 à 10 peuvent être inversés et le rendement de l'investissement initial sera le même.
Exemple 7.3 Calcul du taux de rendement de l'investissement moyen (iRAI)
Calculez le taux de rendement sur l'investissement moyen pour l'usine de merlu congelé de l'exemple 7.3.
Réponse: Afin de déterminer correctement l'investissement moyen, celui-ci doit être calculé conformément au Tableau 7.1
Tableau 7.3 Calcul de l'investissement moyen pour l'usine du Tableau 7.1
|
Année |
Bénéfice annuel moyen ($EU) |
|
1 |
600 000 |
|
2 |
600 000 - 60 000 = 540 000 |
|
3 |
546 000 - 60 000 = 480 000 |
|
4 |
492 000 - 60 000 = 420 000 |
|
5 |
420 000 - 60 000 = 360 000 |
|
6 |
360 000 - 60 000 = 300 000 |
|
7 |
300 000 - 60 000 = 240 000 |
|
8 |
240 000 - 60 000 = 180 000 |
|
9 |
180 000 - 60 000 = 120 000 |
|
10 |
120 000 - 60 000 = 60 000 |
|
Total |
3 300 000 ÷10 = 330 000 |
D'après le Tableau 7.3, le diviseur de l'équation (7.9) est:
Ia + Iw = $EU 330 000 + $EU 60 000 = $EU 390 000
et le taux de rendement de l'investissement moyen sera:
En effectuant une approximation avec l'équation (7.8) on remarque que:
qui montre une erreur de 8,5% dans l'estimation. La valeur temps de l'argent n'est pas considérée, étant donné que seul l'investissement moyen est utilisé, et non pas sa mise en œuvre dans le temps.
Cette méthode compare la valeur actualisée (VA) de tous les flux de trésorerie avec l'investissement initial. Elle suppose des opportunités égales de réinvestissement des flux de trésorerie à un taux d'intérêt pré-assigné. Ce taux peut être considéré comme la valeur moyenne du taux de rendement du capital de la compagnie ou considéré comme le rendement minimum acceptable pour le projet. La procédure suivie compare l'importance de la valeur actualisée de tous les revenus avec l'investissement au temps 0. La valeur actualisée nette est un montant simple par référence au temps zéro et représente une prime s'il est positif, ou un déficit s'il est négatif, à un taux de rendement fixe choisi.
La valeur actualisée peut également être définie comme le montant supplémentaire qui sera nécessaire au début du projet, à un taux d'intérêt pré-assigné, pour générer un revenu égal, et au même moment que l'investissement prévu. Les résultats n'indiquent pas l'importance du projet. Pour cette raison, le rapport du flux de trésorerie diminué par rapport à l'investissement est également suggéré comme critère (Equation 7.12)
Cette relation peut être utilisée comme un indicateur de la rentabilité d'un projet en analysant la différence entre le résultat et la valeur unitaire. L'unité est là où le rendement prédéterminé coïncide avec la valeur du taux interne du rendement (paragraphe 7.3.3). Les résultats des deux calculs (Equations 7.11 et 7.12) peuvent donner une idée de l'importance totale du projet.
Exemple 7.4 Calcul de la valeur actualisée
Calculez: a) la valeur actualisée (VA) et b) la relation de VA' pour l'usine de merlu congelé de l'exemple 7.1.
Réponse: En appliquant un taux i = 15% par an dans l'équation (7.11) on obtient les résultats suivants:
Il faut noter que la valeur à la casse et le fonds de roulement doivent être inclus dans le flux de trésorerie de l'année précédente.
a) VA = 770 182 $EU - 660 000 $EU = 110 182 $EU
A la fin des dix ans, le flux de trésorerie du projet, composé sur la base du revenu de fin d'année sera:
F = 137 000 × (1,15)9 + 153 000 × (1,15)8 + 153 000 × (1,15)7 + 153 000 × (1,15)6 + 153 000 × (1,15)5 + 153 000 × (1,15)4 + 153000 × (1,15)3 + 153 000 × (1,15)2 + 153 000 × (1,15) + 213 000 = $EU 3 115 816
Ce montant représente la valeur future du procédé pour le projet et doit égaler la valeur future de l'investissement initial plus la VA composée à un taux d'intérêt de 15% par an.
F = (660 000 +110 182) × (1,15)10 = $EU 3 115 816
Ainsi, lorsque 110 182 $EU sont rajoutés à l'investissement (660 000 $EU) le résultat sera la somme qui devrait être investie à 15%, pour générer un revenu annuel égal et au même moment que ce qui est estimé par l'investissement recommandé.
b) Relation entre la VA du flux de trésorerie annuel et l'investissement total de l'équation (7.12)
Cette méthode prend en compte les intérêts de l'argent investi, avec le temps, et est basée sur la partie de l'investissement qui n'a pas été récupérée à la fin de chaque année pendant la vie utile du projet.
On utilise une méthode par essais-erreurs pour établir le taux d'intérêt à appliquer au flux de trésorerie chaque année, de telle manière que l'investissement initial soit réduit à zéro (ou valeur à la casse, plus valeur du terrain, plus fonds de roulement) pendant la vie utile du projet.
Dans un tel cas, le taux de rendement résultant est équivalent au taux d'intérêt maximum qui doit être acquitté pour obtenir les fonds nécessaires pour financer l'investissement et permettre de le rembourser intégralement à la fin de la vie utile du projet.
Ainsi, avec cette méthode, la valeur actualisée de tous les flux de trésorerie est considérée égale à zéro et le taux de rendement interne, r, est calculé par tâtonnements:
DCFRR = TRI = r, où:
Il faut noter que l'informatisation du calcul des estimations de faisabilité est devenue courante. Les systèmes informatisés d'estimation des bénéfices ont une gamme étendue d'applications, qui sont utilisées pour augmenter la précision et réduire le temps et le coût de préparation des estimations de ressources-emploi des fonds et de bénéfice.
Exemple 7.5 Calcul du taux de rendement interne ®
Calculez le taux de rendement interne pour l'usine de merlu surgelé de l'exemple 7.1
Réponse: Au bout de 10 ans, la VA des CF (exprimée en dollars) sera de:

qui est égale à la valeur actualisée de l'investissement initial fixe, plus le fonds de roulement.
VA = IF + Iw = $EU 660 000.........(7.15)
Un taux de rendement interne est obtenu en portant l'équation (7.14) au même niveau que l'équation (7.15) et en trouvant la valeur de r par essais et erreurs. Comme indiqué précédemment, cette recherche par essais et erreurs peut être effectuée sur ordinateur, mais sans cela, un facteur de réduction est normalement appliqué aux flux de trésorerie annuels, afin d'obtenir la valeur actualisée en appliquant différentes valeurs de r, jusqu'à ce que la valeur requise de l'investissement soit obtenue.
Le facteur de réduction pour les paiements à la fin de l'année M est:
où:
r = taux d'intérêt choisi
M = année pour laquelle le calcul a été effectué
Le Tableau 7.4 montre la méthode par essais et erreurs utilisée dans l'exemple.
Tableau 7.4 Calcul du taux de rendement interne pour l'unité de traitement de poisson de l'Exemple 7.1
|
|
|
Essai pour r = 0,1 |
Essai pour r = 0,2 |
r = 0,19 | |||
|
Année(m) |
Flux de trésorerie |
Facteur dm |
Valeur actualisée |
Facteur dm |
Valeur actualisée |
Facteur dm |
Valeur actualisée |
|
0 |
(660) |
|
|
|
|
|
|
|
1 |
137 |
0,909 |
125 |
0,833 |
114 |
0,840 |
115 |
|
2 |
153 |
0,826 |
126 |
0,694 |
106 |
0,705 |
108 |
|
3 |
153 |
0,751 |
115 |
0,579 |
89 |
0,592 |
91 |
|
4 |
153 |
0,683 |
104 |
0,482 |
74 |
0,497 |
76 |
|
5 |
153 |
0,621 |
95 |
0,402 |
61 |
0,417 |
64 |
|
6 |
153 |
0,564 |
86 |
0,335 |
51 |
0,350 |
54 |
|
7 |
153 |
0,513 |
78 |
0,279 |
43 |
0,294 |
45 |
|
8 |
153 |
0,466 |
71 |
0,232 |
35 |
0,247 |
38 |
|
9 |
153 |
0,424 |
65 |
0,194 |
30 |
0,207 |
32 |
|
10 |
213 |
0,385 |
82 |
0,162 |
35 |
0,174 |
37 |
|
Total |
|
|
948 |
|
638 |
|
660 |
|
| |||||||
|
|
|
1,44 |
|
0,97 |
|
1,00 | |
L'interpolation pour déterminer la valeur correcte de r peut être effectuée en portant la relation entre l'investissement initial et la VA totale en fonction de r, comme indiqué sur la Figure 7.2.
Figure 7.2 Interpolation pour le calcul de r en utilisant les données du Tableau 7.4
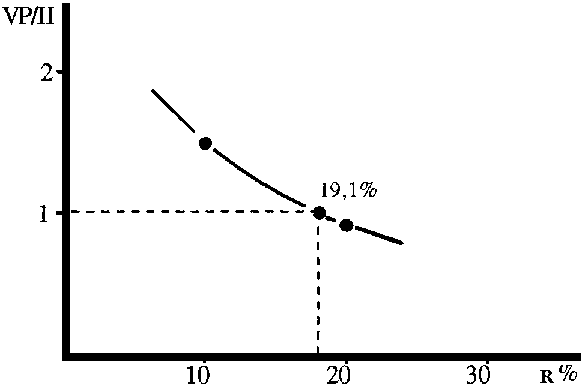
Pour plus de simplicité, certaines colonnes pour le facteur dM ont été omises dans le Tableau 7.4. Le taux de rendement de 19,1% est le taux d'intérêt auquel le montant initial de $EU 660 000 devrait être placé pour générer un revenu comparable et au même moment que celui calculé pour l'investissement proposé. Ainsi:
1) 660 000 × 1.19= 785 697; 785 697-137 000 = 648 697
2) 648 697 × 1.19 = 772 241; 772 241-153 000 = 619 241
3) 619 241 × 1.19 = 737 176; 737 176 - 153 000 = 584 176
4) 584 176 × 1.19 = 695 432; 695 432 - 153 000 = 542 432
5) 542 432 × 1.19 = 645 738; 645 738 - 153 000 = 492 738
6) 492 738 × 1.19 = 586 580; 586 580-153 000 = 433 580
7) 433 580 × 1.19 = 516 156; 516 156 - 153 000 = 363 156
8) 363 156 × 1.19 = 432 319; 432 319 - 153 000 = 279 319
9) 279 319 × 1.19 = 332 515; 332 515-153 000 = 179 515
10) 179 515 × 1.19 = 213 000; 213 000-213 000 = 0
Il faut souligner que le taux de rendement interne calculé pour l'usine dans l'exemple est inférieur aux rendements observés pour des usines similaires mais plus grandes. Ce résultat, conformément à la réalité, est justifié par les concepts discutés au chapitre 5.
Le temps de retour sur investissement est défini comme la période de temps minimale théoriquement nécessaire pour récupérer l'investissement initial sous forme de flux de trésorerie du projet, en se basant sur les recettes totales moins les coûts et amortissements.
Exemple 7.6 Calcul du temps de retour sur investissement (nR)
Calculez le temps de retour sur investissement pour l'usine de merlu congelé de l'exemple 7.1
Réponse: L'application de cette méthode aux données du Tableau 7.1, indique le temps nécessaire pour réduire l'investissement à zéro. A partir de l'équation (7.17):
valeur approchée qui n'est égale à la valeur réelle que lorsque les flux de trésorerie sont égaux.
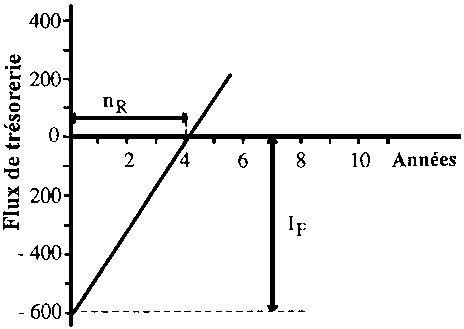
Le Tableau 7.5 montre que l'investissement sera réduit à zéro entre 4 et 5 ans.
Les valeurs du Tableau 7.5 sont portées sur la Figure 7.3. Cette figure montre l'interpolation graphique qui donne un temps de retour sur investissement de 4,05 ans. C'est la valeur réelle de nr.
Tableau 7.5 Flux de trésorerie cumulé pour l'usine du Tableau 7.1
|
Année |
Flux de trésorerie ($EU) |
Flux de trésorerie cumulé ($EU) |
|
0 |
- 600 000 |
- 600 000 |
|
1 |
137 000 |
- 463 000 |
|
2 |
153 000 |
- 310 000 |
|
3 |
153 000 |
- 157 000 |
|
4 |
153 000 |
- 4 000 |
|
5 |
153 000 |
149 000 |
|
6 |
153 000 |
302 000 |
|
7 |
153 000 |
455 000 |
|
8 |
153 000 |
608 000 |
|
9 |
153 000 |
761 000 |
|
10 |
153 000 |
914 000 |
Figure 7.3 Interpolation graphique pour obtenir le temps de retour sur investissement
Les investissements en capital sont réalisés dans le but d'obtenir un bénéfice annuel substantiel, mais la possibilité de perte existe toujours. Ce facteur, qui accompagne tout investissement, est appelé «risque». En général, plus grand est le risque, plus le taux de rendement escompté sera élevé et plus court sera le temps prévu pour récupérer l'investissement.
Le Tableau 7.6 qui donne les valeurs moyennes pour les taux de rendement annuels sans risque des investissements en capitaux dans l'industrie de transformation, permet des comparaisons avec les résultats des nouvelles études de faisabilité sur l'expansion ou la modification des usines existantes (Rudd et Watson, 1968; Woods, 1975).
D'après l'équation (7.3), avec d égale à e et constante, le bénéfice net de risque (NRP) est défini comme:
NRP = (S - C - d × IF) × (1 -t) - iM × (IF + IW) .........(7.20)
Tableau 7.6 Valeurs de rentabilité moyenne du capital sans risque pour les industries de transformation
|
Industrie |
Taux annuel (%) |
|
Services publics (électricité et gaz) |
6,3 |
|
Compagnies de téléphone |
6,8 |
|
Acier (USA) |
7,5 |
|
Général Motors |
7,8 |
|
Standard Oil |
8,2 |
|
Cellulose et papier, caoutchouc |
8-10 |
|
Fibres synthétiques, produits chimiques et pétroliers |
11-13 |
|
Médicaments et produits pharmaceutiques, industries d'extraction et minière |
16-18 |
Dans le Tableau 7.7, le rendement minimum acceptable de rentabilité (iM) est présenté comme une fonction du degré de risque (Happel et Jordan, 1981).
Tableau 7.7 Quantification du risque
|
Type de projet |
Niveau de risque |
iM(%) |
|
Projet court, modification des installations |
faible |
10-15 |
|
Equipement spécifique |
modère |
15-25 |
|
Instrumentation automatique |
élevé |
20-50 ou plus |
Un résultat supérieur à zéro indique que la rentabilité annuelle du projet dépasse le rendement minimum acceptable, même lorsque le risque est pris en considération. Cette méthode ne considère pas la valeur temporelle de l'argent, mais des équations plus complètes, par exemple la méthode valeur-risque, sont indiquées dans la littérature (Happel et Jordan, 1981).
Exemple 7.7 Calcul du profit net de risque (PNR) Calculez le profit net de risque pour l'usine de merlu congelé de l'exemple 7.1.
Réponse: Un taux de rentabilité minimum acceptable de 10% a été choisi à partir du Tableau 7.1. Ceci est considéré comme une alternative à faible risque. A partir de l'équation (7.20):
PNR = 91 400 - 0,10 × 660 000 = $EU 25 400
Un résultat supérieur à zéro indique que la rentabilité annuelle du projet dépasse le rendement minimum acceptable, même lorsque le risque est pris en considération. Il reste au lecteur à déterminer la rentabilité de l'usine de conserves dans l'exemple 2.2 en utilisant la méthode employée dans les exemples 7.1 à 7.7.
Données:
IF = $EU 130 000 (de l'exemple 3.2)
IW = $EU 13000 (de l'exemple 3.2)
Production quotidienne = 2 670 boîtes
Nombre de jours de travail par an = 250
n = 10 ans
Prix de vente = $EU 0,8/boîte
Coût de production unitaire = $EU 0,68/boîte (exemple 4.5)
Les méthodes de rendement sur investissement fixe ou moyen donnent des valeurs statiques qui peuvent entraîner des résultats erronés. Ces "valeurs de point" sont applicables pour une année particulière ou pour des années "moyennes". Néanmoins, elles représentent la solution la plus facile pour une estimation rapide. Le temps de retour sur investissement ne rend pas suffisamment compte des dernières années de vie utile du projet. D'autre part, la méthode du taux de rendement interne considère la valeur temps de l'argent et produit des résultats plus réalistes que les autres méthodes. S'il y a des investissements après le lancement, la valeur actualisée est la méthode qui doit être utilisée, étant donné que la méthode du taux de rendement interne fournit des résultats multiples.
Quel est le meilleur critère de rentabilité? En pratique, l'analyste n'utilise pas un critère unique, mais considère l'utilisation de critères variés pour compenser les avantages et les inconvénients de chacun. Le Tableau 7.8 donne des valeurs raisonnables pour le temps de retour sur investissement et le taux de rentabilité interne pour les projets présentant différents degrés de risque (Cunningham, 1980).
Tableau 7.8 Valeurs types pour le temps de retour sur investissement et le taux de rendement interne en fonction du risque
|
Projet |
Temps de retour sur investissement |
Taux de rendement interne |
|
Risque élevé |
< 2 |
> 20 |
|
Risque normal |
< 5 |
15 |
|
Risque faible |
|
< 10 |
Les facteurs-clés qui affectent la rentabilité des opérations dans les usines de poisson sont en général le coût et la qualité de la matière première et le rendement du traitement, tant que la matière première est disponible et que le marché des produits de transformation est stable (Montaner and Zugarramurdi, 1994).
L'analyse de rentabilité est une méthode d'organisation et de présentation de certaines des relations statiques d'économie à court terme d'une affaire. Les diagrammes économiques de production montrent comment les coûts, les ventes et les bénéfices varient lorsque le taux de production change, les autres choses étant égales. Ces évaluations ne tiennent pas compte de la valeur temps de l'argent et les données concernant les décisions sont considérées comme raisonnablement précises.
Le meilleur modèle connu de seuil de rentabilité relie les coûts variables et fixes au revenu pour la planification des bénéfices. En général, l'efficacité des opérations de production dépend de l'utilisation de l'usine. Lorsque le bénéfice peut être défini comme une fonction du niveau de production du système, il est possible de sélectionner le niveau de production pour lequel les profits seront les plus élevés. D'un point de vue mathématique:
- Revenu total = prix de vente ($EU/unité) × taux de production (unités/temps) = P × Q.........(7.21)- Coûts totaux = coût variable ($EU/unité) × taux de production (unités/temps) + TFC ($EU/temps) = V × Q + TFC.........(7.22)
- Bénéfice net avant impôts = BNAI = revenu total - coûts totaux = P × Q - (V × Q + TFC) .........(7.23)
Au seuil de rentabilité, le bénéfice est égal à zéro et la production pour le seuil de rentabilité peut être calculée comme suit:
Q = TFC/(P - V) .........(7.24)
La valeur Q indique le volume pour lequel le revenu et le coût de fonctionnement total se compensent exactement. En ce point, une unité supplémentaire fabriquée et vendue génère un bénéfice. Jusqu'à ce que le seuil de rentabilité soit atteint, le producteur fonctionne à perte. Les effets du taux de production et du temps de fonctionnement sur les coûts doivent être reconnus. En considérant la demande de vente avec la capacité et les caractéristiques de fonctionnement de l'équipement, l'analyste peut recommander les taux de production et les calendriers d'opération qui donnent les meilleurs résultats économiques.
Il est généralement admis que les sociétés recherchent un profit maximal. La majorité des théories micro-économiques considère la société comme une entité de maximalisation du profit. A court terme, lorsque le niveau de production peut être modifié mais pas la taille de l'entreprise, la société est placée devant plusieurs alternatives de niveau de production, chacune avec des bénéfices différents, de telle manière que c'est l'alternative présentant les gains les plus importants qui sera choisie.
La quantité que la société produira dépend des caractéristiques du marché. Dans un marché parfaitement concurrentiel, l'équilibre est atteint avec une production industrielle totale de QT et un prix de P*. Chaque société a une demande horizontale qui coupe l'axe vertical au prix d'équilibre (P*). Dans ce cas, les revenus marginal et moyen sont tous deux constants et P* = MR = AR.
Toutes ces relations sont indiquées à la Figure 7.4.
Etant donné que la société peut vendre une quelconque quantité de produit (Q) au même prix, son revenu total (RT) sera une ligne ayant une pente positive et passant par l'origine. Si la société a une structure de coût représentée par les courbes suivantes: Coût total moyen (CTM), Coût marginal (CM), Coût total fixe (CTF) et Coût total (CT), quelle sera la quantité totale (Q*) que la société décidera d'offrir à la vente et quel sera le bénéfice dans ce cas?
Figure 7.4 Equilibre à court terme pour une société opérant sur un marché parfaitement concurrentiel
La réponse à ces questions nécessite de prendre en considération les objectifs d'une société produisant dans un environnement parfaitement concurrentiel: maximaliser le bénéfice ou minimiser les pertes. La manière la plus simple de déterminer le point pour lequel le profit est maximal est de comparer le revenu total et les coûts totaux ou d'égaliser le revenu marginal (RM) et le coût marginal (CM). Ce raisonnement est présenté à la Figure 7.4. La société maximalise le bénéfice en vendant une quantité (Q*) pour laquelle CM = P*. La distance verticale entre la ligne de revenu total et la courbe de coût total indique le bénéfice. Il sera maximum lorsque Q* sera égal au nombre d'unités produites. La fonction de profit de la société est dérivée en soustrayant CT de RT à chaque taux de production. Dans ce système, il est également possible de subir des pertes à court terme et de continuer malgré tout à produire, en fonction du niveau des prix du marché et lorsque cette alternative signifie moins de pertes qu'en cas d'arrêt complet de la production.
La Figure 7.5 montre le cas où la société fait face à des P de plus en plus bas. Le fait que la société réalise un profit ou une perte dépend de la relation entre le prix et le coût total moyen à l'intersection de RM et de CM. Les quantités à produire (Qd, Qc, Pb et Pa) sont déterminées comme:
Prix = Coût Marginal- Le point (Qd, Pd) maximalise le bénéfice dû au fait que le prix Pd excède ATC.
- Le point (Qc, Pc) est le point du seuil de rentabilité, le bénéfice est égal à zéro. Le prix Pc est égal à ATC.
- Le point (Qb, Pb) minimise ses pertes sur le court terme du fait que le prix Pb est inférieur à ATC mais supérieur à AVC. Ainsi les TFC sont payés et les TVC sont partiellement récupérés.
- Le point (Qa, Pa) est un point de fermeture, le profit négatif est égal à TFC ou Pa = AVC. Des pertes sur le court terme égales à TFC seront subies si la production est temporairement arrêtée.
Cette conclusion est utile pour dériver la courbe d'approvisionnement pour la société, à court terme (voir Figure 7.5). La courbe de maximalisation de l'approvisionnement de la société est sa courbe ascendante de coût marginal.
A court terme, la capacité d'une société est limitée par ses entrées fixes, alors qu'à long terme, les options sont nombreuses: sa taille peut changer, de nouvelles technologies peuvent être mises en place, ou les caractéristiques de ses produits peuvent changer suivant les modifications des aspirations des consommateurs. Chaque entreprise doit déterminer sa courbe d'approvisionnement à long terme comme une extrapolation de ces concepts. En réalité les variations interviennent en fonction de la structure de la concurrence; c'est-à-dire que selon qu'il y ait peu ou beaucoup de fournisseurs ou que les produits soient identiques ou variés. On peut identifier quatre types de structure de marché:
- Concurrence parfaite: nombreux fournisseurs pour un produit standardisé
- Concurrence monopolistique: nombreux fournisseurs pour un produit varié
- Oligopole: peu de fournisseurs pour un produit standard ou varié
- Monopole: un seul fournisseur pour un produit sans substitut.
Exemple 7.8 Détermination du seuil de rentabilité pour une usine de poisson congelé
Analysez l'usine de merlu congelé de l'exemple 2.1. Portez les coûts totaux, les coûts variables, le coût fixe et le revenu à partir des courbes de vente sur un graphe et déterminez le seuil de rentabilité.
Réponse:
Données:
Prix de vente = $EU 1 560/tonne de blocs de filets de merlu
Coût de production unitaire = $EU 1 272/tonne BF (Exemple 4.4)
Coût unitaire variable = $EU 1085,5/tonne BF (Exemple 4.4)
Coût unitaire fixe = $EU 186,5/tonne BF (Exemple 4.4)
Capacité journalière = 2 tonnes BF Nombre de jours de travail par an = 270
Les équations (7.21) et (7.22) sont utilisées pour calculer TR, TVC, TFC, TC et NPBT sur l'intervalle de capacité de 0 à 100%.
- Revenu annuel = $EU 1 560/tonne BF × Q (tonnes BF/an) = 1 560 × $EU Q/an
Coût de production annuel =
$EU 1 085,5/tonne BF × Q (tonnes BF/an) + $EU 186,5/tonne BF × 540 tonnes BF/an =
$EU (1 085,5 × Q+100710)/an
Le seuil de rentabilité peut être calculé à partir de l'équation (7.24):
N = 100 710/(1 560-1 085,5) = 210 tonnes BF/an
Le Tableau 7.9 et la Figure 7.6 montrent la variation des différents paramètres.
Tableau 7.9 Revenus, coûts et bénéfices pour les différents niveaux de production pour une usine de merlu congelé
|
Pourcentage |
Q |
TR |
TVC |
TFC |
TC |
NPBT |
|
0 |
0 |
0 |
0 |
100,71 |
100,71 |
-100,71 |
|
20 |
108 |
168,48 |
117,23 |
100,71 |
217,94 |
- 49,46 |
|
40 |
216 |
336,96 |
234,47 |
100,71 |
335,18 |
1,78 |
|
60 |
324 |
505,44 |
351,70 |
100,71 |
452,41 |
53,03 |
|
80 |
432 |
673,92 |
468,94 |
100,71 |
569,65 |
104,27 |
|
100 |
540 |
842,40 |
586,17 |
100,71 |
686,88 |
155,52 |
La Figure 7.6 illustre la relation entre le coût fixe et le coût total et le niveau de production, de même qu'entre le revenu et le niveau de production.
Figure 7.6 Représentation graphique du seuil de rentabilité pour une usine de merlu congelé
Pour un diagramme du seuil de rentabilité linéaire, les opération sont bénéficiaires à la droite du points du seul de rentabilité (39% de l'utilisation de l'usine ou 210 tonnes BF par an ou 0,78 tonne BF par jour). Si la production est inférieure, l'opération est déficitaire. Des gains sont obtenus si la production est plus élevée.
Exemple 7.9 Détermination du seuil de rentabilité pour une usine de farine de poisson
Analysez le seuil de rentabilité pour l'usine de farine de poisson de l'exemple 5.3, qui traite 500 tonnes de matière première par jour.
Réponse: La Figure 7.7 montre le graphe du seuil de rentabilité pour les valeurs données dans le Tableau 5.6 pour l'usine de 500 tonnes/jour.
Dans les pêcheries artisanales qui exploitent un grand nombre d'espèces, les prix sont fréquemment fixés par ou pour différentes espèces de taille identique. Ces groupes peuvent ou non avoir des caractères biologiques similaires. Pour les espèces d'intérêt commercial, le prix est fixé d'une manière directement proportionnelle à la préférence du consommateur. Ces prix sont généralement stables, bien qu'ils soient susceptibles de varier considérablement pendant certaines saisons du fait des variations des volumes capturés, de la variété des espèces et pendant des manifestations culturelles ou religieuses. Il en résulte une différence des revenus perçus par chaque entreprise au cours d'une année donnée (Stevenson et al., 1982).
Afin d'améliorer leur balance économique, les pays concernés soutiennent les petites pêcheries avec différentes méthodes de financement. Par exemple, au Ghana et au Sénégal, le gouvernement a mis en place un système qui s'oriente surtout vers une réduction des taxes sur le gas-oil qui est utilisé par les bateaux de pêche et les canots depuis plus de 10 ans. Cette politique de réduction des coûts de fonctionnement a une influence favorable sur la motorisation dans les deux pays. Au Ghana, les prix ont été réduits de 0,8 $EU à 0,25 $EU par litre, tandis qu'au Sénégal ils sont inférieurs au prix normal de 0,50 $EU par litre.
Parfois ce type de politique peut créer des distorsions, si des moteurs plus puissants que ceux nécessaires sont achetés, et que des treuils mobiles plutôt que fixes sont utilisés, ce qui augmente les coûts opérationnels du secteur et de l'économie en général (Greboval, 1989).
Une autre étude menée aux Seychelles (Parker, 1989) a montré que si les petits bateaux rencontrent des difficultés économiques, les bateaux compris entre 8 et 13 m de long souffrent également du fait de la plus grande quantité de capital investi dans chaque unité de pêche. Pour cette raison, le rendement économique de trois unités de bateaux de pêche de ce type fait l'objet d'une analyse:
1. Modèle standard (avec moteur de 27-37 CV)2. Modèle standard avec écho-sonde et moulinets électriques (choisis car on effectue de meilleures prises)
3. Semblable au second modèle, avec une capacité égale, mais avec un moteur de 70 CV (11,6 m de long)
Le revenu d'une expédition peut être considéré comme une fonction des prix, du taux de capture obtenu par les types d'équipements de pêche utilisés, de la composition des prises et de la durée du voyage (limitée par la capacité à entretenir le bateau). Dans le premier exemple, le revenu estimé par voyage est de $EU 1 558 et de $EU 2 833 pour les autres.
Le paramètre le plus important, en relation avec le revenu total, est le nombre de voyages que peut effectuer le bateau pendant une période de pêche donnée. Ces coûts de fonctionnement et de financement sont couverts plus facilement si le bateau opère de façon plus intensive. Cependant, le manque d'entretien adéquat va réduire les flux de trésorerie et un flux de trésorerie réduit va réduire la disponibilité des fonds pour l'entretien, créant ainsi un cercle vicieux.
La question est ouverte pour savoir quel est le taux de rentabilité raisonnable pour le propriétaire du bateau étant donné que le taux d'intérêt bancaire pour un pêcheur souhaitant emprunter est de 10% ou plus (bien que cela puisse être acceptable pour ceux qui sont habitués à manipuler des capitaux importants).
Il est difficile d'administrer un investissement qui rapporte seulement 14% lorsqu'il faut payer 10% pour les prêts. Le Tableau 7.10 analyse les moyens de renverser la situation en éliminant une taxe sur le gas-oil (colonne 3), en augmentant le prix des captures de 10% (colonne 4) et en jouant simultanément sur ces deux effets (colonne 5). Pour un bateau standard, on considère une moyenne de 2-2,5 voyages par mois. Pour les bateaux 2 et 3, seul le nombre maximum de voyages a été considéré. Pour les propriétaires de bateaux qui veulent passer à des moteurs de capacité supérieure (bateau 3) il est presque impossible de rembourser les prêts sans augmenter le prix de vente des captures ou de réduire les coûts de fonctionnement (Parker, 1989).
Tableau 7.10 Taux de rendement sur l'investissement initial (%) pour les navires 1,2 et 3
|
|
Investissement |
Base |
iROI1 |
iROI2 |
iROI3 |
|
Navire 1 |
33 480 |
5,64 |
8,56 |
9,36 |
12,29 |
|
Navire 1 |
33 480 |
11,79 |
15,54 |
16,44 |
20,10 |
|
Navire 2 |
67 500 |
14,24 |
17,76 |
18,44 |
21,87 |
|
Navire 3 |
72 540 |
9,3 |
13,30 |
14,27 |
18,26 |
Des résultats d'essais effectués le long des côtes de Karnataka (Inde) peuvent être mentionnés (Nordtheim et al., 1980). L'utilisation d'eau de mer réfrigérée (RSW) pour la manipulation et le transport des espèces pélagiques a été étudiée en tant qu'élément du programme FAO pour améliorer l'utilisation des petits pélagiques. L'objectif était d'augmenter l'utilisation pour la consommation humaine, la qualité et la durée de conservation, ainsi que la valeur marchande de ces matières premières. Des fonds dont la valeur s'élève à $EU 53 424 ont été investis pour adapter les cales à l'utilisation d'eau de mer réfrigérée; l'analyse financière a donné les valeurs suivantes pour un bateau de 13,36 m de long avec une moyenne de prises annuelle de 600 tonnes:
|
VA nette |
- $EU 25 440 (i = 15%) |
|
TRI |
- 47% |
Temps de retour sur investissement - pendant la troisième année
Un autre exemple est constitué par des études économiques sur les bateaux péchant les espèces pélagiques (pour ne citer que l'anchois), qui ont été menées au Pérou. La méthode VA définie par l'équation (7.12) a été appliquée afin de déterminer la rentabilité. Un taux de réduction de 15% a été envisagé en se basant sur les taux d'intérêt des emprunts souscrits et en incluant les coûts administratifs et les commissions. La Figure 7.8 illustre la variation de rentabilité en fonction de la dimension de la cale, pour différents taux d'intérêt.
Différentes analyses économiques sont traitées ci-après pour différentes usines de poisson de petites et moyennes dimensions. Une analyse économique a été effectuée pour les conserveries de petits poissons dans les pays tropicaux, pour la production de 10 000 (modèle 1) et 20 000 (modèle 2) boîtes de 125 g de sardines toutes les 8 heures. Le remplacement des machines (modèle 1) par de la main-d'oeuvre (modèle 3) a également été évalué en même temps.
Le Tableau 7.11 montre les valeurs résultant de l'application des méthodes du taux de rendement interne et des valeurs actualisées, utilisant un taux de réduction de 10% pour la dernière méthode, qui est le taux choisi par le Tropical Products Institute pour l'évaluation des projets. On considère une vie utile de 10 ans.
Tableau 7.11 Evaluation de la rentabilité des petites conserveries de poisson
|
Valeur actualisée (i = 10%) ($EU) |
Modèle 1 |
Modèle 2 |
Modèle 3 |
|
|
Taux de rendement interne ® |
1 262 100 |
2 678 910 |
1 153 382 |
|
|
61,5% |
69,5% |
59,0% |
||
|
A) 200 jours/an |
47,5% |
54,0% |
45,0% |
|
|
|
150 jours/an |
33,5% |
38,5% |
31,5% |
|
B) 50% sur marché intérieur |
33,5% |
39,0% |
29,5% |
|
|
C) +25% Coûts de production |
36,7% |
42,6% |
32,0% |
|
Une analyse de sensibilité a également été effectuée en utilisant les paramètres suivants:
(A) réduction du nombre de jours de travail par an (200 et 150); B 50% de la production sont vendus sur le marché intérieur; (C) 25% d'augmentation des coûts de fonctionnement. Le modèle de base considérait 250 jours/an et l'exportation de 100% de la production, où des prix plus élevés que ceux du marché intérieur (60%) pouvaient être obtenus.
Le taux de rendement interne ® diminue de 38,5% en moyenne. Si les deux premiers paramètres sont considérés ensemble, les valeurs obtenues sont inférieures de 50% et les résultats sont négatifs lorsque le troisième facteur est incorporé (Edwards et al., 1981). Le Tableau 7.12 montre les investissements requis et le TRI pour les conserveries de poisson et de fruits de mer en Indonésie (Bromiley et al., 1973).
Tableau 7.12 Taux de rendement interne ® pour les conserveries de poisson en Indonésie
|
Site |
Capacité annuelle |
Investissement total |
r |
|
Bitung |
104 (thon) |
1 850 000 |
36 (*) |
|
Pare-Pare |
720 (thon) |
360 000 |
35 |
|
Central Java |
3 840 (crevettes) |
810 000 |
45 |
(*) Le calcul du taux de rendement interne ® est affecté par l'intérêt qui doit être payé par l'investissement; si la moitié de l'investissement est financée par un prêt de 10 ans avec un taux d'intérêt annuel de 12%, la valeur du taux de rendement interne sera de 52%.
Le taux de rendement interne calculé pour une conserverie mécanisée en Norvège, avec une capacité de production de 15 tonnes/jour de matière première (sardines), était de 27,1% (Myrseth, 1985). Il existe des évaluations là où il est commode d'exprimer les résultats en fonction de variables dont les estimations sont incertaines. Par exemple, la performance économique des usines de congélation de blocs entiers de poisson a été étudiée afin de calculer le prix à payer pour la matière première, si l'on considérait des taux de rendement favorables de 10 et 20%, avec une vie utile de 15 ans pour les investissements. Les résultats sont résumés au Tableau 7.13.
Tableau 7.13 Prix de la matière première calculé pour les taux de rendement interne de 10 et 20%
|
|
Prix de la matière première |
||
|
r = 10% |
r = 20% |
||
|
Production annuelle: 2 240 tonnes |
|||
|
|
Investissement: 322 430 $EU |
|
|
|
|
Prix de vente: 228 $EU/tonne |
109 |
94 |
|
Production annuelle: 3 360 tonnes |
|||
|
|
Investissement: 535 480 $EU |
|
|
|
|
Prix de vente: 228 $EU/tonne |
380 |
243 |
Deux niveaux de production ont été étudiés. Dans le premier cas, 2 240 tonnes de poissons entiers ont été utilisées annuellement, avec deux équipes de 8 heures par jour, travaillant 250 jours/an. Dans le second cas, 3 360 tonnes ont été utilisées, avec une équipe supplémentaire de 8 heures, une capacité de réfrigération et une fabrication de glace augmentées. Si les coûts de l'énergie diminuent de 50%, le prix d'achat de la matière première peut augmenter de 17 $EU/tonne. Un taux de rendement interne de 18,5% a été calculé pour un cas hypothétique impliquant une usine de farine de poisson, avec un investissement de 10 000 $EU (sur une période de 5 ans) (FAO, 1986a). Dans les petites unités de fumage du poisson, la distribution des bénéfices est similaire à celle pratiquée par les pêcheurs artisanaux. Le revenu généré par les opérations de l'usine est partagé équitablement entre les employés de l'usine avec une part pour «l'association», une fois les coûts opérationnels déduits. Si l'usine fonctionne avec trois employés, le revenu est divisé en quatre parts; une pour chaque employé et une pour le groupement (FAO, 1986a).
Au Sri Lanka, on a réalisé une évaluation de la production d'ensilage liquide pour une usine ayant une capacité annuelle de 450 tonnes de produit, à trois prix de vente différents, en prenant une valeur de 33 $EU/tonne et des pourcentages de dépréciation de 20 et 25%. La détermination des taux de rendement interne pour une vie utile de 5 ans a fourni les valeurs de 77,38 et 26% respectivement. Ces chiffres indiquent que le projet sera hautement rentable (Aagaard et al., 1980; Disney et James, 1980).
Une autre analyse économique montre la production d'ensilage liquide à partir des captures secondaires des crevettiers au Mexique. L'investissement fixe s'élève à 28 289 $EU et le fonds de roulement à 6 667 $EU pour une production annuelle de 312 t d'ensilage. Les coûts de production sont de 92 $EU/tonne en considérant une période d'amortissement de cinq ans. Le prix de vente a été calculé avec un taux de rendement interne de 15%. Le prix de l'ensilage montrait des avantages significatifs lorsqu'on le comparait aux prix d'autres sources de protéines et de la farine de poisson. Il faut ajouter que le coût par unité de protéine est avantageux, même lorsque des espèces et des intrants (acide) sont utilisés dans la production (Edwards et Disney, 1980). En général, il apparaît que la production d'ensilage liquide est avantageuse, mais des considérations particulières doivent être faites à propos de la distance entre l'usine et l'utilisateur et la compétitivité des prix des autres aliments. Il n'y a pas de doutes sur l'avantage nutritionnel de son utilisation pour la formulation d'aliments pour porcs (Bertullo, 1989; Andrade et al., 1992; Bello et al., 1992), et sur le potentiel de son utilisation dans la nutrition animale pour oiseaux, animaux à fourrure, poissons d'élevage et veaux.
En complément des études de rentabilité, il est utile d'étudier l'influence de la rentabilité sur chaque composante du revenu, des dépenses et de l'investissement. Cette information va permettre de faire des ajustements fondamentaux pour les paramètres qui montrent le plus d'influence, en laissant une estimation plus large pour les autres paramètres.
Dans une analyse de sensibilité on choisit plusieurs variables avec des conceptions raisonnables, et on les fait varier à des étapes successives, avec un pourcentage de variation autorisé. Les différences de rentabilité obtenues indiquent l'importance de chaque variable étudiée.
Exemple 7.10 Analyse de sensibilité
Effectuez une analyse de sensibilité pour une conserverie en utilisant les conditions du cas de base indiquées dans le Tableau 7.14. Le coefficient relatif est défini comme la relation entre la valeur réelle du paramètre et sa valeur dans l'exemple, en calculant la variation relative du taux de rendement interne de la même manière.
Tableau 7.14 Suppositions pour le cas de base
|
1 |
La vitesse de production est égale aux ventes annuelles |
|
2 |
Capacité de l'usine: 100 000 (boîtes/jour) |
|
3 |
Fonds de roulement comme fonction empirique de l'investissement fixe, des coûts d'opération et des ventes |
|
4 |
Amortissement par la méthode linéaire |
|
5 |
Vie utile estimée: 10 ans |
|
6 |
Taux d'imposition: 45% (valeur moyenne pour l'Argentine) |
|
7 |
Valeur résiduelle zéro |
|
8 |
Pas de coûts financiers |
|
9 |
150 jours/an de production (moyenne pour les conserveries en Argentine) |
|
10 |
Les prix de vente restent constants tandis que les autres paramètres varient |
Réponse:
Le Tableau 7.15 et la Figure 7.9 montrent les résultats de l'analyse de sensibilité.
De petites variations au niveau du prix de vente et des coûts de matière première (poisson et emballage) modifient la rentabilité de l'usine de manière considérable. Cela indiquerait que pour une estimation rapide des coûts et de la rentabilité, ces données devraient être connues avec précision, même lorsque des données précises sur la capacité de l'usine, la MO, les services et les coûts fixes ne sont pas disponibles. Les besoins en matière première doivent être calculés aussi précisément que possible et une étude de marché précise doit être entreprise pour déterminer le prix de vente. Ceci est particulièrement vrai pour les procédés qui ne nécessitent pas un capital important, c'est-à-dire les procédés qui sont contrôlés par des coûts variables. Ici, l'effet du prix de vente sur la rentabilité est approximativement le double de celui des autres paramètres (Cerbini et Zugarramurdi, 1981a).
Tableau 7.15 Analyse de sensibilité
|
Numéro dans |
Paramètre |
Variation |
Valeur relative du taux de |
|
1 |
Prix de vente |
+ 10 |
1,90 |
|
|
- 4 |
0,57 |
|
|
2 |
Taux de production |
+ 20 |
1,14 |
|
|
- 20 |
0,88 |
|
|
3 |
Prix de la matière première |
+ 15 |
0,58 |
|
|
- 15 |
1,35 |
|
|
4 |
Prix des boîtes |
+15 |
0,28 |
|
|
- 15 |
1,56 |
|
|
5 |
Investissement |
+ 20 |
0,64 |
|
|
- 20 |
1,20 |
|
|
6 |
Jours par an |
+ 47 |
1,29 |
|
|
- 25 |
0,83 |
|
|
7 |
Coûts de la main-d'oeuvre |
+ 20 |
0,63 |
|
|
- 20 |
1,31 |
7.9.1 Effet de l'inflation sur la valeur actualisée (VA)
7.9.2 Effet de l'inflation sur le TRI. Taux de retour sur investissement réel
7.9.3 Effet de l'ajustement du fonds de roulement sur le TRI
7.9.4 Relations de l'inflation sous forme continue
7.9.5 Effet du financement du fonds de roulement sur le TRI
7.9.6 Effet des emprunts sur l'investissement et sur le TRI
7.9.7 Effet des emprunts non indexés sur l'investissement sur le TRI
7.9.8 Conclusions générales concernant les situations inflationnistes
L'inflation est un phénomène économique qui est mondialement redouté; les pays développés la surveillent étroitement et les taux d'inflation anticipés et réels sont publiés au moins une fois par mois. De nombreux pays en développement souffrent des effets de l'inflation. Elle peut être due à de multiples raisons, habituellement liées à des décisions macro-économiques et politiques, comme l'émission de monnaie sans support correspondant. Des informations supplémentaires sur le concept d'inflation sont données dans l'Annexe B.5, Le Tableau 7.16 montre des séries de taux d'inflation dans plusieurs pays d'Amérique latine où l'on observe en permanence des valeurs élevées (à 2 et 3 chiffres). Les indicateurs d'inflation sont basés sur un échantillon de biens et services choisis pour représenter les besoins matériels du consommateur moyen.
Figure 7.9 Analyse de sensibilité pour les conserves d'anchois, Argentine 1981
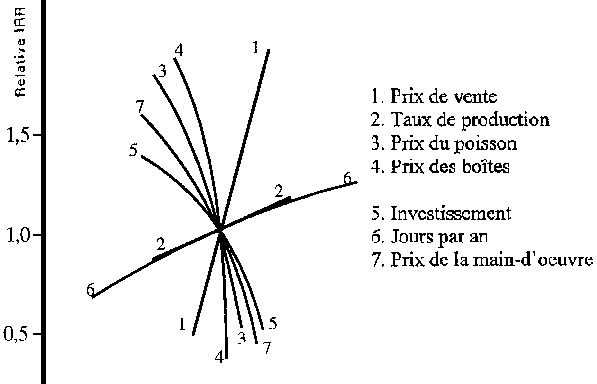
Tableau 7.16 Indice des prix à la consommation (augmentation moyenne en % par an)
|
Année |
Argentine |
Bolivie |
Brésil |
Colombie |
Chili |
Mexique |
Uruguay |
|
1976 |
444,1 |
4,5 |
35,7 |
17,4 |
211,8 |
15,8 |
50,6 |
|
1977 |
176,0 |
8,1 |
40,5 |
28,6 |
91,9 |
28,9 |
58,1 |
|
1978 |
175,5 |
10,4 |
38,3 |
18,7 |
40,1 |
17,5 |
44,5 |
|
1979 |
159,5 |
19,7 |
50,2 |
24,2 |
33,4 |
18,2 |
66,8 |
|
1980 |
100,8 |
47,2 |
77,9 |
27,9 |
35,1 |
26,3 |
63,5 |
|
1981 |
104,5 |
32,2 |
956 |
29,4 |
19,7 |
28,0 |
34,1 |
|
1982 |
164,8 |
92,0 |
89,6 |
23,4 |
9,9 |
58,9 |
19,9 |
Source: (Index Economico, 1984); (Coyuntura y Desarrollo, 1983)
Etant donnée la large base de calcul, ces indices représentent une estimation raisonnable du taux d'inflation pour les autres activités économiques. Une telle inflation est appelée «générale», on suppose que tous les secteurs de l'économie augmentent leurs prix dans les mêmes proportions, contrairement à l'inflation appelée «réprimée» ou «différentielle», dans laquelle, pour des raisons différentes telles que des changements technologiques, des pénuries touchant quelques matières premières, des politiques gouvernementales, etc., les différents facteurs de l'économie peuvent subir l'inflation à des taux différents. Dans les pays subissant des taux d'inflation extrêmes, les déviations «différentielles» deviennent moins importantes et peuvent être ignorées. Ceci peut être observé au Tableau 7.17 qui présente une série de taux d'inflation pour l'Argentine.
Même durant cette période d'intenses changements sociaux et économiques, les variations indiquées au Tableau 7.17 entre les différents secteurs n'excédaient pas 10% ainsi qu'on peut l'observer dans la dernière ligne p du Tableau 7.17.
Tableau 7.17 Indicateurs de l'évolution des prix en Argentine (1970 base = 1)
|
Indice du coût de construction | |||||||
|
Prix à la consommation |
Indice |
Indice général |
Matériaux |
Main-d'oeuvre |
Dépenses générales |
Indice des prix de gros |
Indice des prix agricoles |
|
1970 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
|
1971 |
1 391 |
1 432 |
1 419 |
1 457 |
1 357 |
1 482 |
1 602 |
|
1972 |
2 284 |
2 268 |
2 393 |
2 158 |
2 253 |
2 608 |
3 002 |
|
1973 |
3 283 |
3 659 |
3 623 |
3 742 |
3 426 |
3,41 |
3 506 |
|
1974 |
4 598 |
5,98 |
6 343 |
5 816 |
5 283 |
4 642 |
4 259 |
|
1975 |
20 006 |
28 604 |
36 923 |
21 514 |
26 892 |
20 807 |
16 923 |
|
1976 |
89 536 |
91,00 |
136,27 |
50 836 |
88,822 |
101,18 |
94 593 |
|
1977 |
233,18 |
204,63 |
330,48 |
96,67 |
191 032 |
250,07 |
218,08 |
|
1978 |
629,22 |
517,14 |
810,69 |
262,81 |
475,89 |
608,43 |
557,60 |
|
1979 |
1 508,46 |
1 251,50 |
2 036,11 |
567,61 |
1 159,61 |
1 392,45 |
1 203,12 |
|
1980 |
2 830,40 |
2 527,30 |
3 905,96 |
1 300,63 |
2 481,07 |
2 192,57 |
1 637,98 |
|
1981 |
6 545,96 |
5 247,30 |
8 320,66 |
2 61 1,65 |
4 768,25 |
6 143,51 |
25 123,00 |
|
1982 |
20 276,10 |
19 322,70 |
31 635,40 |
9 167,80 |
15 881,40 |
25 268,50 |
21 209,50 |
|
1983 |
108 208,90 |
127 361,00 |
181 936,00 |
79 248,90 |
104 299,00 |
129 013,00 |
103 829,60 |
|
b |
93,50 |
93,50 |
100,90 |
83,30 |
91,60 |
94,30 |
91,80 |
b: Indice moyen d'inflation (par la méthode des moindres carrés)
Bien qu'il semble que la plupart des pays, y compris les pays développés, évoluent actuellement (1995) vers des conditions plus stables et moins inflationnistes, les sociétés de transformation du poisson opèrent dans le monde réel et sont donc susceptibles de devoir lutter pour survivre dans des conditions inflationnistes. L'inflation affecte les calculs de rentabilité des projets d'investissement, rendant difficiles et confuses les analyses et la prise de décision. Ceci est particulièrement vrai dans les pays où des taux d'inflation élevés sont pratiquement la règle, comme c'était le cas de l'Argentine et d'autres pays d'Amérique latine.
Cette partie traitera exclusivement de l'influence de l'inflation générale sur l'analyse de rentabilité d'un projet, montrant la différence entre le bénéfice réel et celui que l'on pourrait qualifier seulement de résultat numérique produit par un processus inflationniste.
L'utilisation d'une devise stable pour les valeurs du flux de trésorerie est une procédure habituelle pour trouver les valeurs du «taux de rendement interne réel». Cependant, en considérant les composantes du flux de trésorerie qui sont indépendantes du taux d'inflation, par exemple l'amortissement des prêts et la valeur réelle du fonds de roulement, l'application des valeurs du flux de trésorerie en devise stable pour le calcul du TRI réel n'est pas valable et les formules décrites doivent être modifiées (de Santiago et al., 1987).
Les effets de la prise en compte de l'inflation sur les méthodes de VA et du taux de rendement interne sont d'abord analysés en les appliquant à l'exemple de l'usine de congélation.
L'équation (7.11) est valable dans le cas d'une inflation zéro. Si l'inflation a un taux fractionnaire (3, cette équation peut être écrite sous la forme:
Lorsque b = 0, l'équation (7.25) est la même que l'équation (7.11) avec iR (taux réel) = i
Exemple 7.11 Calcul de la valeur actualisée (VA) en tenant compte de l'inflation
Calculez la valeur actualisée (VA) pour l'usine de congélation de l'exemple 7.1. Prenez un taux annuel d'inflation de 80%, en supposant que l'usine est située en Argentine.
Réponse: Le taux de change est de 10 000 australes/1$EU (1990). En conséquence, si le Tableau 7.1 est exprimé en australes, la valeur sera celle indiquée dans le Tableau 7.18.
En appliquant l'équation (7.11), la valeur actualisée du projet à la fin de l'année 10 est de 1 102 millions d'australes.
Tableau 7.18 Tableau ressources-emploi de fonds pour une unité de transformation de poisson lorsqu'il n'y a pas d'inflation (en '000 millions d'australes (A))
|
Activité |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
|
RESSOURCES | ||||||||||
|
Capital propre |
4,8 |
|
|
|
|
|
|
|
|
|
|
Crédits bancaires (*) |
1,8 |
|
|
|
|
|
|
|
|
|
|
Produit net des ventes |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
|
Total (a) |
15,02 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
|
EMPLOI DES FONDS | ||||||||||
|
Investissements fixes |
6,0 |
|
|
|
|
|
|
|
|
|
|
Fonds de roulement |
0,6 |
|
|
|
|
|
|
|
|
|
|
Coûts financiers (**) |
0,27 |
|
|
|
|
|
|
|
|
|
|
Coûts de production |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
|
Total (b) |
13,74 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
|
(a) - (b) |
1,29 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
|
Profit net (***) |
0,77 |
0,93 |
0,93 |
0,93 |
0,93 |
0,93 |
0,93 |
0,93 |
0,93 |
0,93 |
|
Moins amortissements |
0,60 |
0,60 |
0,60 |
0,60 |
0,60 |
0,60 |
0,60 |
0,60 |
0,60 |
0,60 |
|
Flux de trésorerie |
1,37 |
1,53 |
1,53 |
1,53 |
1,53 |
1,53 |
1,53 |
1,53 |
1,53 |
1,53 |
(*) 30% IF = 1 800 millions d'australes (**) 15% Taux annuel (***) En déduisant l'impôt sur les bénéfices (40%)
L'exemple peut être modifié en appliquant un taux annuel d'inflation de 80%, mais sans tenir compte de l'effet de l'inflation et en appliquant incorrectement l'équation 7.11. Les données pour cette situation sont fournies au Tableau 7.19, et ont un résultat de 221 800 millions d'australes en valeur actuelle.
Tableau 7.19 Tableau ressources-emploi de fonds pour une usine de transformation de poisson avec inflation (b = 0,8) (en '000 millions d'australes (A))
|
Activité |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
|
RESSOURCES | ||||||||||
|
Capital propre |
4,8 |
|
|
|
|
|
|
|
|
|
|
Crédits bancaires (*) |
1,8 |
|
|
|
|
|
|
|
|
|
|
Produit net des ventes |
15,2 |
27,3 |
49,1 |
88,4 |
159,2 |
286,5 |
515,7 |
928,3 |
1671,0 |
3007,8 |
|
Total (a) |
21,8 |
27,3 |
49,1 |
88,4 |
159,2 |
286,5 |
515,7 |
928,3 |
1671,0 |
3007,8 |
|
EMPLOI DE FONDS | ||||||||||
|
Investissements fixes |
6,0 |
|
|
|
|
|
|
|
|
|
|
Fonds de roulement |
0,6 |
|
|
|
|
|
|
|
|
|
|
Coûts financiers (**) |
0,5 |
|
|
|
|
|
|
|
|
|
|
Coûts de production |
12,4 |
22,3 |
40,1 |
72,1 |
129,8 |
233,6 |
420,5 |
756,9 |
1362,5 |
2452,5 |
|
Total (b) |
19,4 |
22,3 |
40,1 |
72,1 |
129,8 |
233,6 |
420,5 |
756,9 |
1362,5 |
2452,5 |
|
(b) - (b) |
2,3 |
5,0 |
9,1 |
16,3 |
29,4 |
52,9 |
95,2 |
171,4 |
308,5 |
555,3 |
|
Profit net (***) |
1,4 |
3,0 |
5,4 |
9,8 |
17,6 |
31,7 |
57,1 |
102,8 |
185,1 |
333,2 |
|
Moins amortissements |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
|
Flux de trésorerie |
2,0 |
3,6 |
10,4 |
10,4 |
18,2 |
32,3 |
57,5 |
103,4 |
185,7 |
333,8 |
(*) 30% IF = 1 800 millions d'australes (**) 15% Taux annuel (***) En déduisant l'impôt sur les bénéfices (40%)
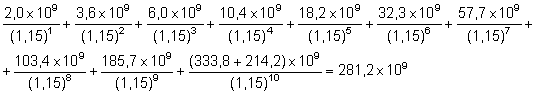
VA = (281,2 - 6,60) × 109 = 274,6 × 109 , soit VA = 274 000 millions d'australes
Prendre en compte l'inflation et appliquer correctement l'équation (7.25) génère un résultat tout à fait différent et révèle que le projet a en réalité une VA négative.
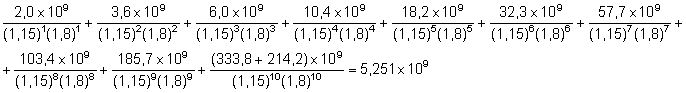
VA = (5,251 - 6,60) × 109 = - 1,349 × 109, donc VA = - 1 349 millions d'australes
Cet exemple montre que l'effet de l'inflation fait paraître un projet plus profitable qu'il n'est en réalité. Ceci pourrait être le cas de beaucoup d'échecs d'investissements par le passé dans les pays en développement.
L'inflation affecte le calcul de profitabilité des projets d'investissement, rendant les analyses et les prises de décision difficiles, surtout dans les pays où prédomine un taux d'inflation élevé. En fait, il affecte négativement les possibilités d'investissement.
Le concept bien connu de taux réel d'intérêt (Riggs, 1977; Barish et Kaplan, 1978) sera utilisé, lequel est basé sur le raisonnement suivant: considérer un fond Io qui, en un an, a dégagé un intérêt (Io × i); le montant total sera alors de:
I1 = Io × (1 + i) .........(7.26)
Si durant cette période il y avait un taux d'inflation de b, le rapport entre la valeur réelle de I1 (appelée I10) et la valeur de Io serait:
I10 = I1/(1 + b) = Io × (1 + i)/(1 + b) .........(7.27)
Un taux réel d'intérêt Ir (prenant en compte l'effet de l'inflation) (Jelen et Black 1983; Jones, 1982) peut être défini par l'expression:
I10 = Io × (1 + Ir) .........(7.28)
En rendant équivalentes les équations (7.27) et (7.28), on peut déduire ce qui suit:
Cette formule diffère de celle communément utilisée:
Ir - (taux approximatif réel de retour sur investissement) = i - b.........(7.30)
qui n'est valable que quand b < 1 (Holland et Watson, 1977; Estes et al., 1980; Shasshua et Goldschmidt, 1985). Elle donne une estimation du taux réel d'intérêt plus élevé que celui défini par l'équation (7.29) Ayant défini l'erreur relative (e) par l'équation (7.31), il coïncidait avec le taux d'inflation
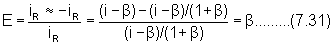
En introduisant le concept de taux réel d'intérêt défini par l'équation (7.29), un taux interne réel de retour est déterminé quand l'équation (7.32), en référence au flux de trésorerie réduit, est égale à zéro.
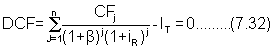
ou CFj est le flux de trésorerie net de l'année j et n le nombre de périodes dans la vie du projet. Si l'économie est affectée par un phénomène général d'inflation le numérateur de chaque terme de la somme est supposé avoir été augmenté par le taux d'inflation:
CFj = CFjo (1 + b)j.........(7.33)
Quand on additionne l'équation (7.33) à (7.32) on peut observer que l'utilisation du flux de trésorerie en valeur constante amène aux valeurs du "taux de retour interne réel" (TRI).
Exemple 7.12 Calcul du taux de rentabilité interne, TRI ®
Calculer le taux de rentabilité interne pour l'usine de congélation de colin de l'exemple 7.1. Utiliser un taux annuel d'inflation de 80%.
Réponse:
Du tableau 7.19, on obtient une valeur de r = 96.9%. En calculant le TRI à partir d'un flux de trésorerie net corrigé par l'inflation, on obtient un Ir de 11%. A partir de l'équation (7.29):
Ce résultat montre à nouveau l'effet de l'inflation dans un cas qui semblait profitable, quand l'inflation n'est pas prise en compte. Cependant, en pratique, plusieurs composantes du flux de trésorerie peuvent être indépendantes du taux d'inflation, tel que: amortissement des emprunts, paiement d'intérêts, paiement des taxes, ajustement du capital de travail, etc.; ceci empêchant l'utilisation du flux de trésorerie en monnaie constante pour le calcul d'un TRI réel.
Pour faire face au problème de l'inflation, certains de ces concept devront être analysés en un simple flux de trésorerie consistant en un investissement initial dégageant un flux de trésorerie constant quand le taux d'inflation est de zéro sur une période de 10 ans.
L'inflation oblige à augmenter le fond de roulement IW. Pour étudier l'effet de cette augmentation sur la profitabilité il est admis que le fond de roulement peut être exprimé en fractions (frW) des ventes annuelles "S". Prenant en compte que les ventes annuelles (S) et les coûts annuels de fonctionnement (C) sont augmentés par l'inflation:
CFj = Sj - Cj = S0 × (1 + b)j - Co × (1 + b)j.........(7.34)
Mais cela peut induire la nécessité d'une augmentation annuelle du fonds de roulement par:
Iwj = fIW × Sj-i × (1 + b) - fIW × Sj-1 = fIW × Sj-1 × b.........(7.35)
et le capital accumulé pourrait être récupéré à la fin de l'année N
IWN = fIW × SN.........(7.36)
En fin de compte, la formule du TRI (avant taxes) est transformée en:
et avec quelques changements:
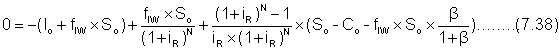
et l'équation suivante est dérivée:
L'effet de l'inflation sur la profitabilité réelle ip par la dévaluation du fonds de roulement est exprimé par l'équation (7.38). Pour analyser une telle influence les rapports dimensionnels suivants sont remplacés dan l'équation (7.38):
r= So/Co et X = Co/Io
et l'équation entière est divisée par Io, donnant ainsi l'expression finale:
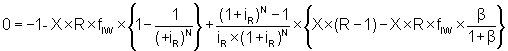
Un panorama de l'inflation montrant les différents paramètres que renferme l'équation (7.40) est illustré sans le Tableau 7.20.
Tableau 7.20 Taux de rentabilité interne réel
|
GP* |
Iw* |
b =0,0 |
0,2 |
0,5 |
1,0 |
1,5 |
2,0 |
4,0 |
|
0,3 |
0,1 |
0,2247 |
0,2269 |
0,2089 |
0,1906 |
0,1794 |
0,1719 |
0,1567 |
|
0,3 |
0,2013 |
0,1554 |
0,1072 |
0,0559 |
0,0230 |
---- |
---- |
|
|
0,5 |
0,1703 |
0,1033 |
0,0310 |
---- |
---- |
---- |
---- |
|
|
0,7 |
0,1471 |
0,0641 |
---- |
---- |
---- |
---- |
---- |
|
|
0,5 |
0,1 |
0,4440 |
0,4280 |
0,4120 |
0,3958 |
0,3861 |
0,3795 |
0,3665 |
|
0,3 |
0,3720 |
03306 |
0,2886 |
0,2456 |
0,2192 |
0,2013 |
0,1648 |
|
|
0,5 |
0,3191 |
0,2586 |
0,1960 |
0,1306 |
0,0893 |
0,0607 |
0,00002 |
|
|
0,7 |
0,2788 |
0,2032 |
01240 |
0,0390 |
---- |
---- |
---- |
|
|
0,7 |
0,1 |
0,6320 |
0,6166 |
0,6011 |
0,5855 |
0,5762 |
0,5700 |
0,5575 |
|
0,3 |
0,5326 |
0,4930 |
0,4530 |
0,4127 |
0,3883 |
0,3720 |
0,3390 |
|
|
0,5 |
0,4595 |
0,4016 |
0,3429 |
0,2830 |
0,2462 |
0,2213 |
0,1703 |
|
|
0,7 |
0,4035 |
0,3313 |
0,2575 |
0,1810 |
0,1333 |
0,1004 |
0,0314 |
Note:
Le Tableau 7.20 montre que le taux de rentabilité interne réel est détérioré par l'inflation. Cette réduction devient plus prononcée à mesure que le fonds de roulement acquière plus d'importance relative. Dans le but de maintenir la profitabilité de la compagnie, l'action immédiate des dirigeants serait d'accroître le prix de vente des produits en relation avec les coûts, en supposant que cela soit possible sans réduire le volume des ventes.
Cette stratégie est représentée par l'équation (7.41) par R'>R. Dans le but de maintenir la constante iR résultante dans l'équation (7.41), l'augmentation proportionnelle (R'/R) peut être obtenue par l'équation (7.40) avec b = 0 et la valeur originelle R.
Pour une «profitabilité avant taxes» iR = 0,3, les valeurs de l'équation (7.41) sont présentées à la Figure 7.10. Cette figure permet d'observer que le facteur approprié peut atteindre des valeurs élevées, et qu'il y a alors une augmentation des prix produisant un effet multiplicateur sur les indices d'inflation.
Une analyse utilisant une formule continue est adaptée dans le cas de dévaluations du fonds de roulement, du fait de taux élevés d'inflation, ainsi l'ajustement peut être fait par courtes périodes. Pour un intérêt continu, de simples déductions amènent les relations suivantes:
Valeur future: F(t) = F(o) × exp(i × t) .........(7.42)
Valeur future en monnaie constante: Fo(t) = F(o) × exp (i × t) × exp(-b × t) .........(7.43)
Définition du taux réel d'intérêt: Fo (t) = F(o) × exp(iR × t) .........(7.44)
Il est important de noter que dans le cas continu, l'équation approximative (7.30) est valide. L'équation résultante pour le calcul de TRI sans inflation est donné par:
0 = - (Io + fIW × S) + fo (S-C) × exp(-I × t) dt + fIW × S × exp(-I × tn) = - Io + {[S-C)/i]-(fIW × S)} × {1 -exp(-I × tn)} .........(7.45)
où le i qui met a zéro l'égalité de l'équation (7.45) est le taux de rentabilité interne (TRI). Quand l'inflation est prise en compte, les définitions suivantes peuvent être utilisées:
S = So × exp(b × t) .........(7.46)C = Co × exp (b × t) .........(7.47)
Iw = fIW × S = fIW × So × exp (b × t) .........(7.48)
Avec ces expressions, l'équation qui défini le taux de rentabilité interne réel sera:
En introduisant le concept de taux d'intérêt réel (cas continu iR = i - b), l'équation intégrée est:
En utilisant les relations X et R, et en divisant par Io, l'équation (7.51) se transforme en (7.52), qui est l'expression continue équivalente à l'équation (7.40)
et l'expression continue de (R'/R) correspondant à (7.41)
Les équations "continues" (7.52) et (7.53) montrent un effet défavorable comparé aux formes annuelles similaires discrètes et cela est plus marqué quand le taux d'inflation augmente. Les équations continues montrent que dans une analyse de profitabilité, l'étude par période annuelle peut conduire à de sérieuses erreurs. Pour certains taux d'inflation, l'analyse de l'équation (7.53) montre que des valeurs élevées de fIW du R'/R permettant une profitabilité raisonnable ne seraient pas possibles. En conséquence, les entreprises doivent diminuer leur fonds de roulement et accepter des profitabilités faibles. La persistance du phénomène d'inflation conduirait à des pertes de capital.
Quelques secteurs de l'économie n'ont pas la possibilité de modifier les prix de vente de leurs produits, comme c'est le cas pour les industries exportatrices ou les économies ouvertes avec une parfaite compétition entre pays étrangers. Dans de telles circonstances, une autre ressource valable est l'utilisation d'emprunts qui peuvent améliorer ou détériorer la profitabilité du projet en relation avec le taux d'intérêt fixé. De plus le montant de l'investissement fait par la firme est réduit, changeant aussi le TRI.
Il y a une grande variété de types d'emprunts, cependant seulement ceux permettant une certaine généralisation seront analysés. Premièrement on analysera le financement du fond de roulement année par année. Un emprunt doit être totalement amorti en une période j.
En payant un taux d'intérêt ip et en contractant un nouveau prêt:
fIW × So × (1+b)j
Dans ce cas l'équation qui définit le TRI est la suivante:
ou avec la relation sans dimensions:
L'équation (7.55) est obtenue à partir de l'équation (7.40) en utilisant p = 0. Elle montre le taux d'intérêt minimum ip qui pourrait être payé pour financer le fond de roulement tout en gardant une profitabilité constante égale au cas du zéro inflation.
IP = iR ×(1+b).........(7.56)
Dans quelques cas étudiés au tableau 7.20 les figures de ip calculées à partir de l'équation (7.56) sont présentées dans le Tableau 7.21. Si une profitabilité constante est désirée, un taux d'intérêt plus élevé que l'inflation pourrait être payé seulement à des taux d'inflation bas. A des taux d'inflation élevés, des taux d'intérêt bas (incluant des intérêts négatifs) doivent être payés. Alors même qu'il est inutile de maintenir le niveau de profitabilité, le financement du fond de roulement par des emprunts à un taux d'intérêt plus bas que le niveau de profitabilité total du projet (incluant l'inflation) pourrait amener une nette amélioration sur la profitabilité réelle, mais la perte provenant de l'inflation ne suffit pas quand les valeurs données par l'équation (7.56) n'atteignent pas la profitabilité du projet.
Tableau 7.21 Taux d'intérêt (Ip) pour le financement du fonds de roulement en rentabilité constante
|
GP* |
IW* |
iR=0 |
b =0,2 |
0,5 |
1,0 |
1,5 |
2,0 |
|
0,3 |
0,7 |
0,1471 |
0,1765 |
0,2206 |
0,2942 |
0,3677 |
0,4413 |
|
0,5 |
0,1703 |
0,2043 |
0,2554 |
0,3406 |
0,4257 |
0,5109 |
|
|
0,3 |
0,2013 |
0,2418 |
0,3019 |
0,4026 |
0,5032 |
0,6039 |
|
|
0,1 |
0,2447 |
0,2436 |
0,3670 |
0,4894 |
0,6117 |
0,7341 |
|
|
0,5 |
0,7 |
0,2788 |
0,3345 |
0,4182 |
0,5576 |
0,6970 |
0,8364 |
|
0,5 |
0,3191 |
0,3829 |
0,4786 |
0,6382 |
0,7977 |
0,9573 |
|
|
0,3 |
0,3720 |
0,4464 |
0,5580 |
0,7440 |
0,9300 |
1,1160 |
|
|
0,1 |
0,4440 |
0,5328 |
0,6660 |
0,8880 |
1,1100 |
1,3320 |
A partir des cas présentés dans le Tableau 7.20, les rentabilités réelles, qui pourraient être obtenues en finançant le fonds de roulement à un taux d'intérêt ip = b (taux neutre réel d'intérêt), sont présentées au Tableau 7.22 et montrent d'importantes améliorations par rapport aux valeurs données au Tableau 7.20.
Tableau 7.22 Taux de rentabilité avec financement du fonds de roulement à des taux neutres
|
GP* |
IW* |
b =0,2 |
0,5 |
1,0 |
1,5 |
2,0 |
4,0 |
|
0,3 |
0,1 |
0,2538 |
0,2341 |
0,2141 |
0,2018 |
0,1936 |
0,1768 |
|
0,3 |
0,2141 |
0,1510 |
0,0814 |
0,0346 |
---- |
---- |
|
|
0,5 |
0,1726 |
0,0560 |
---- |
---- |
---- |
---- |
|
|
0,7 |
0,1287 |
---- |
---- |
---- |
---- |
---- |
|
|
0,5 |
0,1 |
0,4733 |
0,4558 |
0,4381 |
0,4275 |
0,4204 |
0,4061 |
|
0,3 |
0,4381 |
0,3845 |
0,3298 |
0,2961 |
0,2732 |
0,2262 |
|
|
0,5 |
0,4025 |
0,3111 |
0,2141 |
0,1510 |
0,1056 |
0,0000 |
|
|
0,7 |
0,3664 |
0,2341 |
0,0814 |
---- |
---- |
---- |
|
|
0,7 |
0,1 |
0,6795 |
0,6625 |
0,6455 |
0,6353 |
0,6285 |
0,6148 |
|
0,3 |
0,6455 |
0,5943 |
0,5428 |
0,5117 |
0,4908 |
0,4487 |
|
|
0,5 |
0,6114 |
0,5255 |
0,4381 |
0,3845 |
0,3482 |
0,2732 |
|
|
0,7 |
0,5772 |
0,4557 |
0,3298 |
0,2499 |
0,1936 |
0,0064 |
L'utilisation d'un emprunt finançant un pourcentage de l'investissement total amorti en parts égales en monnaie constante (emprunt avec paiements indexés) sera analysée. Il est admis que l'amortissement du prêt se fera en N paiements, où:
N = durée de vie économique du projet
Montant de l'emprunt p × Io; 0< p <1
Amortissement: Aj = p × Io × Fp (ip, N) (1 +b)J
c'est-à-dire, le facteur annuité. Il s'ensuit que le taux de rentabilité interne réel est la racine de l'équation dimensionnelle suivante:
L'intérêt stipulé est équivalent au taux interne réel de rendement d'un investissement équivalent au montant emprunté. Il est alors évident que si ip < iR où iR est le projet de rentabilité sans le prêt du point de vue de l'emprunteur, la rentabilité serait améliorée. Néanmoins à mesure que l'inflation augmente et que la rentabilité diminue au-dessous du taux d'intérêt de l'emprunt, ce dernier peut être très onéreux. Un effet opposé est observé pour iR < 0,1 dans les résultats présentés au Tableau 7.23, où iR est la rentabilité du projet avec un emprunt à un taux d'intérêt de ip = 0,1.
Tableau 7.23 Variation du taux réel de rendement en fonction du taux d'inflation pour des emprunts indexés sur l'investissement
|
P=0,7 |
b =0 |
0,2 |
0,5 |
1,0 |
1,5 |
2,0 |
4,0 |
|
Cas 1 | |||||||
|
GP*=0,3 |
ir = 0,2013 |
0,1554 |
0,1072 |
0,0559 |
0,0230 |
---- |
---- |
|
Iw*=0,3 |
ir' = 0,2983 |
0,2083 |
0,1142 |
0,0130 |
-0,0530 |
---- |
---- |
|
Cas 2 | |||||||
|
GP* =0,5 |
ir = 0,3191 |
0,2586 |
0,1960 |
0,1306 |
0,0893 |
0,0607 |
0,00002 |
|
Iw*=0,5 |
ir' = 0,4789 |
0,3723 |
0,2637 |
0,1518 |
0,0820 |
0,0338 |
-0,06780 |
|
Cas 3 | |||||||
|
GP*=0,7 |
ir = 0,4035 |
0,3313 |
0,2575 |
0,1810 |
0,1333 |
0,1004 |
0,0314 |
|
Iw*=0,7 |
ir' =0,5843 |
0,4663 |
0,3472 |
0,2259 |
0,1514 |
0,1006 |
-0,0045 |
Pour augmenter la rentabilité, le taux d'intérêt de l'emprunt doit être moins élevé que le taux de rendement interne (incluant le taux réel plus le taux d'inflation) indépendamment de n'importe lequel des schémas d'amortissement appliqués. Cette conclusion peut être déduite d'une étude de l'équation sans dimensions suivante:
où l'on a considéré:
Montant de l'emprunt p × Io 0<p<1
Amortissement: Aj = p × Io × Fp (ip, N)
Le fait que iR' > iR quant i > ip est montré dans le Tableau 7.24. Ce type d'emprunt devrait avoir des difficultés à faire face aux possibles augmentations du taux d'inflation.
Tableau 7.24 Variation du taux de rentabilité interne en fonction du taux d'inflation pour les emprunts non-indexés. Taux d'intérêt de l'emprunt ip = 0.72; Part d'investissement financée p = 0.70
|
GP* |
Iw* |
b =0,2 |
0,5 |
1,0 |
1,5 |
2,0 |
4,0 |
|
Cas 1 |
ir = 0,2013 |
0,1554 |
0,1072 |
0,0559 |
0,0230 |
---- |
---- |
|
GP*=0,3 |
i = 0,2013 |
0,3865 |
0,6608 |
1,1118 |
1,5575 |
---- |
---- |
|
Iw* =0,3 |
ir' = -------- |
0,01009 |
0,0938 |
0,1037 |
0,0908 |
---- |
---- |
|
Cas 2 |
ir = 0,3191 |
0,2586 |
0,1960 |
0,1306 |
0,0893 |
0,0607 |
0,00002 |
|
GP*=0,5 |
I = 0,3191 |
0,5103 |
0,940 |
1,2612 |
1,7232 |
2,1821 |
4,0001 |
|
Iw* =0,5 |
ir' = 0,0557 |
0,1774 |
0,2115 |
0,1914 |
0,1632 |
0,1388 |
0,07755 |
|
Cas 3 |
ir = 0,4035 |
0,3313 |
0,2575 |
0,1810 |
0,1333 |
0,1004 |
0,0314 |
|
GP*=0,7 |
I = 0,4035 |
0,5976 |
0,8862 |
1,3620 |
1,8332 |
2,3012 |
4,157 |
|
Iw* =0,7 |
ir' = 0,1811 |
0,2891 |
0,2893 |
0,2468 |
0,2075 |
0,1764 |
0,1030 |
Dans le cas de taux d'inflation élevés, le phénomène d'inflation générale de tous les facteurs inclus dans le flux de trésorerie réduit prédomine, et l'utilisation des valeurs en monnaie stable conduit à la détermination du taux de rentabilité interne réel. Cependant l'inflation produit un besoin de reconstitution continue du fonds de roulement qui entraîne des baisses de la rentabilité pouvant atteindre des valeurs relativement élevées.
Ceci peut être corrigé, quand c'est possible, par l'augmentation des marges de vente ou en utilisant des emprunts. Dans ce cas, il est démontré que son efficacité s'efface avec l'augmentation de l'inflation, et peut conduire à des effets inverses. En particulier, les emprunts indexés (parmi lesquels, les emprunts en monnaie étrangère dont le taux de change suit le taux d'inflation générale) représentent un risque important, puisqu'une augmentation du taux d'inflation conduirait à des pertes considérables.
Les équations obtenues pour les flux de trésorerie avec des résultats répétés dans le temps quantifient ces concepts, montrant les valeurs calculées dans les tableaux comme une fonction des paramètres dimensionnels qui représentent les rapports: des ventes sur les coûts de fonctionnement, des coûts de fonctionnement sur les investissements fixes, du fonds de roulement sur les ventes. Une généralisation de cas continu montrerait le besoin d'analyses à court terme, étant donné que les analyses sur des périodes annuelles pourraient conduire à de grandes erreurs dans le cas de taux d'inflation élevés.
La pratique généralisée d'augmentation des marges de vente (pour couvrir le coût de remplacement) conduirait à un processus inflationniste qui s'auto-entretient, qu'il est difficile, sinon impossible, de contrôler par les mécanismes d'économie classique.
La combinaison de tous ces facteurs, avec les sorties annuelles variables et les taux d'inflation variables, peut être résolue seulement par des flux de trésorerie discontinus, incluant le concept de rentabilité réelle défini par l'expression (7.32). Cependant, les formules présentées comme une fonction des paramètres dimensionnels donnent une idée générale utile de prise de décision sur les stratégies à utiliser dans l'éventualité de taux d'inflation élevés.
Des taux d'inflation élevés, ou l'inflation tout court, ne sont pas une situation recherchée ou désirée par n'importe quelle industrie, mais une situation à laquelle il faut faire face et qu'il faut surmonter pour survivre. A partir de l'expérience dans les pays à taux d'inflation important, il est clair que l'effort d'exploitation le plus important dans de telles situations est dirigé vers un développement des stratégies financières dans le but de survivre. D'autres aspects, tels que le marché et les développements technologiques et de la qualité, reçoivent moins ou pas d'attention. Malheureusement, des taux d'inflation relativement élevés continuent d'être un problème dans beaucoup de pays en développement. C'est pourquoi nous avons trouvé nécessaire d'inclure cette analyse (certainement pas limitée à l'industrie du poisson) pour fournir des outils appropriés au lecteur intéressé.