Most of the quantities involved in fishery research cannot be observed or measured throughout the whole population, e.g. it is virtually impossible to measure all the fish caught, still less all the fish in the sea. A section, or sample, of the whole population is therefore examined for the attributes concerned, e.g. percentage of mature fish, or average size. On the assumption that this sample is in some way representative of the whole population, an estimate can be made of the true value in the population. If the sampling system used is a good one, then the estimate obtained is likely to differ little from the true value. It is the purpose of the present manual to outline methods of developing good sampling systems for the quantities of major interest in fisheries biological research.
Example 1.2.1
Example 1.2.2
Example 1.2.3
Example 1.2.4
Example 1.2.5
Example 1.2.6
Before further discussion of sampling, it is necessary to describe some of the basic statistical concepts used in sampling theory. Statistics deal with the numerical properties of sets (or populations) of objects. Such populations can be real biological populations, e.g. the Rastrelliger in the Indian Ocean, or some other set of definite measurements, e.g. a set of temperatures, or even the possible estimates of a quantity (e.g. mean length of fish) obtained from a definite sampling system. That is, a quantity derived from one population (the lengths of fish) can be a member of another population (the estimates of the mean length). Each member of the population has a numerical value, the variate, which can take a range of possible values (e.g. length of fish). Such a population may be described by its frequency distribution; that is, the frequency with which each of the possible values occurs. A distribution may be either discontinuous, when only certain values are possible - e.g. the throw of a dice can be only one of the values 1, 2, 3, 4, 5 or 6 - or continuous, when all values, at least within a range, can occur, e.g. lengths of fish. A distribution is often represented graphically, either as a histogram or frequency polygon, but for this purpose the values of a continuous variable will usually be grouped. Then for a frequency polygon the height of each point will give the frequency, i.e. the number of individuals having a certain value or occurring in a certain interval (for which it will normally be plotted at the midpoint of the interval); for a histogram the area of each section gives the total frequency in that interval, which will allow different class intervals to be used, e.g. 1-cm groups for small fish and 5-cm for larger fish.
Plot the following data for length-frequency distribution of North Sea cod (from Russell, 1922) as a frequency polygon and as a histogram, first as given (1-cm intervals), and then using groupings of, for example, 2 cm, 3 cm, 5 cm, 10 cm and 20 cm.
|
Length (l) |
Freq. (n) |
l |
n |
l |
n |
l |
n |
l |
n |
l |
n |
|
25 |
2 |
39 |
18 |
53 |
15 |
67 |
|
81 |
|
95 |
|
|
26 |
7 |
40 |
15 |
54 |
8 |
68 |
- |
82 |
2 |
96 |
- |
|
27 |
8 |
41 |
13 |
55 |
6 |
69 |
- |
83 |
1 |
97 |
- |
|
28 |
9 |
42 |
13 |
56 |
11 |
70 |
1 |
84 |
- |
98 |
- |
|
29 |
13 |
43 |
19 |
57 |
7 |
71 |
1 |
85 |
- |
99 |
- |
|
30 |
12 |
44 |
19 |
58 |
4 |
72 |
- |
86 |
1 |
100 |
- |
|
31 |
9 |
45 |
21 |
59 |
5 |
73 |
1 |
87 |
1 |
101 |
- |
|
32 |
15 |
46 |
13 |
60 |
1 |
74 |
- |
88 |
- |
102 |
1 |
|
33 |
7 |
47 |
19 |
61 |
2 |
75 |
- |
89 |
- |
103 |
- |
|
34 |
7 |
48 |
21 |
62 |
1 |
76 |
- |
90 |
- |
104 |
- |
|
35 |
5 |
49 |
8 |
63 |
2 |
77 |
1 |
91 |
- |
105 |
- |
|
36 |
12 |
50 |
22 |
64 |
- |
78 |
1 |
92 |
1 |
|
|
|
37 |
13 |
51 |
18 |
65 |
|
79 |
|
93 |
|
|
|
|
38 |
16 |
52 |
18 |
66 |
2 |
80 |
1 |
94 |
- |
Total: 449 | |
Also plot as a histogram using coarser groupings (e.g. 10 cm, as against 2 cm) for fish over 60 cm.
Compare the effect of using different base points for grouping, e.g. using for the 5-cm groups 25-29, 30-34 etc., or 27-31, 32-36, etc.
The plots should be made on the same effective scale: when using say 2-cm intervals, the frequency in each interval will be about double that when using 1-cm, so that the scale used should be halved, i.e. for 1-cm intervals, 1 fish (n = 1) equals say 10 units on the graph paper; then for 2-cm intervals, 1 fish equals 5 units, and for 5-cm intervals 1 fish equals 2 units. The length scale should be unaltered. Plotted in this way the various polygons and histograms should be nearly identical.
This example illustrates also the problem of the correct choice of class interval. Here the 1-cm interval is too fine, and causes much extra labor in calculation, writing etc. The figures given are only a sample of much more extensive data, from which it may be easily seen that the irregularities extending over one or two 1-cm groups in the table given are purely chance effects. The possible exception is the peak at 50 cm, and low frequency at 49 cm; this exists, though is much less marked, in the complete data. This is probably due to the common recording error of rounding off measurements (often unconsciously); in this case several fish whose lengths actually were 49 (or 51) cm were recorded as 50 cm.
The best grouping to take - in the example probably 3 cm or 5 cm - will depend on the data concerned; the more extensive the data and complex the frequency distribution the more numerous and finer will be the intervals. A fair guide is that the normal maximum number of intervals is around 20, and that except for a few intervals at the tails of the distribution, the numbers in each interval should not fall much below 10.
The table below (from Fitch, 1958) gives the length composition of Pacific mackerel caught off California in the years 1956-57.
|
l = length, in Quarter-centimeters: n = number of fish | |||||||||
|
l |
n |
l |
n |
l |
n |
l |
n |
l |
n |
|
80 |
|
95 |
6 |
110 |
25 |
125 |
19 |
140 |
13 |
|
81 |
|
96 |
|
111 |
24 |
126 |
26 |
141 |
16 |
|
82 |
|
97 |
9 |
112 |
24 |
127 |
13 |
142 |
15 |
|
83 |
1 |
98 |
6 |
113 |
28 |
128 |
22 |
143 |
8 |
|
84 |
|
99 |
10 |
114 |
31 |
129 |
17 |
144 |
5 |
|
85 |
|
100 |
21 |
115 |
19 |
130 |
24 |
145 |
3 |
|
86 |
|
101 |
13 |
116 |
24 |
131 |
20 |
146 |
11 |
|
87 |
1 |
102 |
14 |
117 |
25 |
132 |
14 |
147 |
2 |
|
88 |
1 |
103 |
16 |
118 |
30 |
133 |
18 |
148 |
6 |
|
89 |
2 |
104 |
22 |
119 |
30 |
134 |
27 |
149 |
|
|
90 |
2 |
105 |
33 |
120 |
17 |
135 |
16 |
150 |
|
|
91 |
1 |
106 |
24 |
121 |
28 |
136 |
20 |
151 |
2 |
|
92 |
3 |
107 |
21 |
122 |
31 |
137 |
15 |
153 |
1 |
|
93 |
1 |
108 |
23 |
123 |
16 |
138 |
16 |
154 |
1 |
|
94 |
6 |
109 |
31 |
124 |
28 |
139 |
13 |
156 |
1 |
|
|
|
|
|
|
|
|
|
Total: 1011 | |
Plot these data as a histogram.
Repeat using groupings of 1/2, 1 and 2 cm.
It will be found that many frequency distributions will, when plotted, appear as single peaks with more or less extensive tails above and below the peak. The differences between distributions will appear mainly in differences in the position of the peak - e.g. the peak in Example 1.2.1 lies between 40 cm and 50 cm, and in the extent of the spread on either side of the peak. One or more of three quantities may be used to define the position of the distribution. That most generally used is the arithmetic mean - or more simply just the mean, usually denoted by m.
Thus if ten fish are measured, lengths 15, 19, 17, 22, 14, 13, 18, 17, 16 and 18 cm then
This can be written in a more general form, by denoting the length of the fish by x and adding a suffix to denote the length of a particular fish; in the example above x1 = 15, x2 = 19, etc., and we can write
Further, we can denote by xi, the length of any, unspecified fish - the ith fish, where i may have any of the values 1, 2, 3... 10 and m = 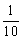 [Sum of xi when i = 1, 2 ... 10]. This can be written in mathematical shorthand, using the symbol S for sum of, and putting the upper and lower limits of i at the top and bottom of the symbol S as,
[Sum of xi when i = 1, 2 ... 10]. This can be written in mathematical shorthand, using the symbol S for sum of, and putting the upper and lower limits of i at the top and bottom of the symbol S as,
Just as the square root symbol 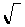 is an instruction to take the square root of the quantity following the symbol, so is the symbol S an instruction about dealing with the quantities following after it. It tells you to add up a set of quantities, all of the same nature, of which the expression following the S sign is a typical member. The numbers above and below the S symbol tell you what particular quantities to add up.
is an instruction to take the square root of the quantity following the symbol, so is the symbol S an instruction about dealing with the quantities following after it. It tells you to add up a set of quantities, all of the same nature, of which the expression following the S sign is a typical member. The numbers above and below the S symbol tell you what particular quantities to add up.
The expression can be shortened further by omitting the i is from the limits when, as usually happens, it is clear that it is i that is taking the values, in this example from 1 to 10
or even shorter when the limits are also clear
Similarly, if we want to write an expression for the mean not of 10 items in particular, but of any, unspecified number, say n (when in the example n = 10) it is
or
or
(1.1)
Also used are the mode, the value at which the actual peak (or peaks) occurs, and the median, or 50 percent point, which is the value such that half the individuals in the population have values less than the median, and half greater. In most distributions the median will lie between the mean and the mode, being rather closer to the mean (as is suggested by the position of the words in a dictionary). The chief use of the mode is not so much in a simple distribution with one peak, but in describing a more complex distribution with several peaks, e.g. the length composition of a catch of fish containing several year-classes. In such a distribution the arithmetic mean may be of much less importance than the values of each peak (e.g. the lengths of each year-class). The mode (or modes) is most easily determined by plotting the data as a histogram or frequency polygon and reading the values from a smooth curve drawn through the plot. It is greatly affected by random variations in the data, so that a rather large sample is required to determine the mode with any precision.
The median is less affected by random errors than the mode, though more than the mean, the latter giving the most precise measure of the position of the distribution. However, particularly when the data are not grouped, or grouped rather finely, the median can be estimated extremely quickly. If the data are not grouped, the estimate of median is given by the central member if the number in the sample is odd, or midway between the two central members if the [number is even. For grouped data a rough estimate of the median is given by the midpoint of the interval in which the central member lies; more precisely it is given by the proportion along the interval. For example in a sample of 101 fish, 40 are less than 16 cm long, 15 lie in the 16/17-cm group, and 46 are over 17 cm. The central member is then the tenth smallest in the 16/17-cm group, and the estimate of the median is 16 + 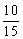 = 16.7 cm.
= 16.7 cm.
Estimate the mean, median and mode of the distribution in Example 1.2.1. Compare the time required to estimate each quantity.
Median is at the 225th fish counting from smallest up, or biggest down, and therefore lies in the 44-cm group. If the measurements of the fish have been recorded to the nearest cm, so that this group contains fish between 43.5 and 44.5 cm, then a more precise estimate of the median is
(Note that two estimates of the median can be made, counting from both the smallest up, and the largest down and these should be checked against each other.)
A definite mode lies near 30 cm with others probably around 40 and 50 cm.
Repeat Example 1.2.3, using the data of Example 1.2.2 both as given and in ½ - cm and 1 - cm groups. Compare your estimate of the position of the modes with the fact that the original data consisted of 6 year-classes of fish, the mean lengths of the year-classes being approximately 21 cm (only 4 fish), 27.5 cm, 31 cm, 33.5 cm and 38 cm (only 3 fish).
The mean (or the mode or median) tells us the position of the distribution - what is the average (or most frequent or central) value of the individuals, i.e. the lengths of the cod in Example 1.2.1 are centered around 50 cm. We also want to know how these lengths vary about this central value - are all the lengths of the fish between 49 and 51 cm, or do they, as in the example, vary between 25 and 100 cm, or even say between 5 and 150 cm. If we take the differences between the individual values and the mean some will be positive and some negative, and the average value will be about zero. We therefore take the square of the difference between the individual value and the mean, and the average value of this squared difference is called the variance. For example, a group of ten fish taken from the population of Example 1.2.1 have lengths
35, 38, 40, 44, 45, 47, 50, 52, 53 and 66 cm
Their mean length is 47.0 cm; the individual differences from the mean are
-12,-9,-7,-3,-2,0,+3,+ 5,+6 and +19 cm
so that the variance of the population formed by the lengths of this small group of fish is
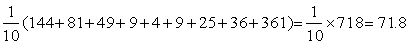
The square root of the variance, which is in some ways an average value of the deviation from the mean, is called the standard deviation. The standard deviation of the population above is 8.45 cm.
In mathematical terms the variance is generally denoted by S2 and the formula for the variance is
(1.2)
where M is the population mean, N total number in the population. If we have a sample of say n individuals from a population, then the estimate of the variance will be1
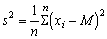 1 It may be noted that the distinction between the true population value of a parameter (mean, variance, etc.) and its value as estimated from a sample is of fundamental importance in statistical theory. In most textbooks the distinction is marked by using Greek letters for the population value, and Roman letters for the estimate. In simple applications the distinction can often be ignored. This is an occasion when the distinction must be observed.
1 It may be noted that the distinction between the true population value of a parameter (mean, variance, etc.) and its value as estimated from a sample is of fundamental importance in statistical theory. In most textbooks the distinction is marked by using Greek letters for the population value, and Roman letters for the estimate. In simple applications the distinction can often be ignored. This is an occasion when the distinction must be observed.
However the true population mean M will usually not be known, and we will have to use the sample mean, m. The estimate of the variance which suggests itself is ns2 = S (xi - m)2; rewriting each item in that summation in terms of M we have
This expression is merely the addition of a number of terms, and by grouping them together in a slightly different order this expression becomes
In the second term the factor 2 (M - m) is common to all the items in the addition, and so can be taken outside the sign; in the third term all the items are the same, and there are n of them, so the expression may be written
(m - M)2 being squared must be positive (or possibly zero if m is exactly equal to M), so that S (xi - m)2 will always be less than, or equal to S (xi - M)2. Therefore 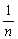 (xi-m)2 will be less than
(xi-m)2 will be less than 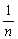 (xi-M)2 and so would give a biased and low estimate of the variance. It can be increased slightly by dividing not by n, but by n-1, and this slight decrease in the divisor can be shown mathematically to balance exactly the degree of bias; that is, for an unbiased estimate of the variance we have
(xi-M)2 and so would give a biased and low estimate of the variance. It can be increased slightly by dividing not by n, but by n-1, and this slight decrease in the divisor can be shown mathematically to balance exactly the degree of bias; that is, for an unbiased estimate of the variance we have
(1.3)
The formulas for mean and variance can be written in several ways for greater simplicity of computation: thus rewriting the formula for the variance we have
which can also be written as
or
(1.4)
The form of 1.4 is suitable for computation particularly on a calculating machine which permits rapid calculation of sums of squares. Suitably arranged, the computations can be to a fair extent self-checking. First calculate S xi and the mean. Then enter x1 on the register and square it, so that on the results register appears xi2, and on the multiplier register, x1. Do not clear these entries, but enter x2 and square it so that on the results and multiplier appears xi2 + x22 and xi + x2 respectively. Repeat for the n numbers, finally obtaining S xi2 and S xi; check that S xi agrees with the value already obtained. This will detect most of the likely errors, e.g. omitting or misreading one value of x.
The calculations may be considerably simplified, and the changes of error reduced, by taking some convenient transformation of the raw data. For instance, suppose the monthly landings of fish during 6 months were 75, 67, 82, 73, 69 and 71 tons; instead of calculating 752 etc., we may take an arbitrary origin at 70 say, and compute the mean and variance of 5,-3,12,3, -1 and 1 (2.83 and 28.17 respectively). Converting back to the original scale, the mean of the original distribution is therefore 2.83 + 70 = 72.83 tons. The variance is unchanged by change of origin so that the variance in the original scale is also 28.17, and the standard deviation s = 5.31.
The above catches might have been expressed in a different scale, as 75,000 ... 71,000 kilograms. Expressed as tons, with origin at 70 tons, we get as before a mean of 2.83, variance 28.17 and standard deviation 5.31. Converting back to kilograms we have to add 70 (to get correct origin) and multiply by 1,000 (to get correct scale), and the mean monthly landings are 72,833 kilograms.
This is a simple example of a transformation which shows that instead of making calculations (sums, sums of squares) concerning the values x, which may be large, we can make the calculations using another set of values y, obtained from x by some direct relation, y = f (x). The simplest is a change of origin, so that
y = x - a (as in the first example, where a = 70)
The means and variances are given by the simple relation, which can be deduced at once from equations 1.1 and 1.2
mean x = Mx = My + avariance of x = Sx2 = Sy2
Another simple transformation is a change of scale.
y = bx (as in the second example, where b equals one thousandth)
Thus
The two transformations may be combined, y = b (x - a)
The weights of fish landed at Rameswaram Island, south India, during the twelve months July 1953 - June 1954 were 205, 218, 150, 136, 89, 55, 112, 28, 93, 105, 186, 253 tons (data from Krishnamurthi, 1957).
Calculate the mean monthly landing, and the variance and standard deviation of the monthly landings; check that the range (253 - 28 = 225 tons) is about 3.2 times the standard deviation.
If the data are arranged in class intervals, e.g. length compositions giving the number in each centimeter group, the arrangement of the calculations for mean and variance are slightly different. The value of each class, e.g. its midpoint, must be included/times, where/is the number of individuals in the class. Thus equations 1.1 and 1.4 must be rewritten as
(1.5)
(1.6)
where k = number of classes
n = number of individuals = S fi
A change of origin before starting computation is likely to be particularly valuable in these calculations; the methods are best described by an example showing the calculation of the mean and the variance of the lengths of Rastrelliger sampled on the Bangkok market in October 1958. The working origin is taken at 17.5 cm, and the working units as half-centimeters.
|
Length group (cm) |
Frequency |
New scale |
|
|
|
xi |
fi |
yi |
fi yi |
fi yi2 |
|
15.5 |
8 |
-4 |
-32 |
128 |
|
16.0 |
7 |
-3 |
-21 |
63 |
|
16.5 |
4 |
-2 |
- 8 |
16 |
|
17.0 |
2 |
-1 |
- 2 |
2 |
|
17.5 |
8 |
0 |
S fi yi = - 63 |
|
|
18.0 |
11 |
+1 |
11 |
11 |
|
18.5 |
2 |
+2 |
4 |
S |
|
19.0 |
3 |
+3 |
9 |
27 |
|
19.5 |
1 |
+4 |
4 |
16 |
|
|
n = 46 |
|
|
S fi yi2 = 271 |
The origin has been chosen near to the probable mean of the distribution - a good choice of origin will reduce the computational work, but a difference of one or two groups either way will not affect work much. The column of values of fi yi is obtained by multiplying the second and third columns together, and the values of fi yi2 can be obtained by multiplying again by yi, without computing yi2 as such. In calculating the mean, the positive and negative values of fi yi are added separately, then
Therefore in the original scale, mean length = 17.5 - 0.38 = 17.12 cm, variance = 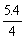 =1.4 cm2, standard deviation =1.2 cm.
=1.4 cm2, standard deviation =1.2 cm.
If the class intervals are not units, so that the scales of x and y may be different, as in the sample above, care should be taken to convert back the results for mean and variance etc. to the proper scale.
All the results obtained by these computations should be checked with a thoroughness corresponding to the accuracy and precision needed in their application. Repetition of the same computations, besides being tedious, is also inefficient in detecting and eliminating errors, as they are not unlikely to be repeated. A good check where accuracy is required is to compute, not only S x and S x2, but also S (x + 1) and S (x + 1)2.
Thus, applied to the data of Example 1.2.1, we would compute
S x = 2 x 25 + 7 x 26 + ... + 1 x 102 = A
and
S x2 = 2 x (25)2 + 7 x (26)2 + ... + 1 x (102)2 = B
and also
S (x + 1) = 2 x 26 + 7 x 27 + ... + 1 x 103 = CS (x + 1)2 = 2 x (26)2 + 7 x (27)2 + ... + 1 x (103)2 = D
In C each fish is 1 unit longer than in A, and since there are 449 fish, if A (and incidentally C) has been calculated correctly, A +449 = C. Similarly D should be bigger than B by a known amount equal to twice the sum of the lengths plus the number of observations, i.e.,
D = B + 2 x A + 449
Calculate for the data in Example 1.2.1 the quantities A, B, C, D above and check that:
(i) C = A + 449(ii) D = B + 2A + 449
and similarly, for the data in Example 1.2.2 which refer to a total of 1,011 fish, calculate S x, S (x + 1) and S x2 and S (x + 1)2 and check that:
(i) S (x + 1) = S x1 + 1011(ii) S (x + 1)2 = S x2 + 2 S x + 1011
These are special cases of the general rules, which will always be followed if no mistakes have been made in the calculations, that:
(i)
(ii)
where n is the number of observations.
A simple check of accuracy (but not of precision) which should always be made is to compute the range of the distribution (greatest value minus least value), and to divide this by the standard deviation. The range will normally be between three and six times the standard deviation, being greatest when there is a single extreme value, and when the number in the distribution is large. It is worth distinguishing accuracy and precision. If a mean length of a number of fish is 43.26 cm, then an estimate of 43.18 cm is very precise and accurate, an estimate of 43 cm is not very precise, but accurate; 37.2 cm is precise, but inaccurate, and 35 cm both imprecise and inaccurate. Precision defines narrowness or otherwise of the limits within which the quantity by implication lies; thus an estimate of 37.2 would presumably include all values from 37.15 to 37.25. The precision is therefore related to the number of significant figures in quantity given. The accuracy is the closeness, or otherwise, of the estimate to the real value.