3.1 Sampling methods for catch and effort statistics
3.2 Sampling for length composition
3.3 Indirect sampling
3.1.1 Statistics required
3.1.2 Definition of population and choice of sampling unit
3.1.3 Estimation of total catch
3.1.4 Estimation of quantity discarded
3.1.5 Effort statistics
The first stage in the study of a fishery is to know what the fishery is catching. All too often catch statistics are nonexistent, or lacking in essential information, e.g. division of the total catch by species or type of fish. Even more often there is no data on the fishing effort, even in the crudest form, e.g. number of boats, number of fishermen. Catch, effort, and their ratio, catch per unit effort, which gives the simplest index of the abundance of the stock, are the basis of the study of any fishery; once any two have been determined, the third can be at once calculated. Thus, the catch per unit effort need not necessarily be determined from the other two, bur rather perhaps the catch and catch per unit effort determined directly, and effort deduced therefrom, or perhaps the catch deduced from data on effort and catch per unit effort. For this reason it is not possible to discuss sampling for catch or effort as separate problems.
Measures of fishing effort
The various uses of effort data and the units required for each must be clearly distinguished. An economist may regard effort as a measure of the economic input, and the catch per unit effort as a measure of the success or efficiency of the fishery. A biologist regards effort as a measure of the mortality caused by fishing, and the catch per unit effort as a measure of the abundance or density of the fish stock. Thus they may require different units of fishing effort, and in particular the units used will change with time in different ways. For example, suppose outboard motors are introduced into a fishery hitherto using only canoes with paddles. To an economist the input has changed little - the main factors, numbers of men or canoes remaining the same - and the catch per unit effort should increase. To the biologist the stock is unaltered and therefore the catch per unit effort should also be unchanged, but the fishing effort should rise. That is, the economist's unit of effort might be the canoe or fisherman, but the biologist requires units of unpowered canoes, a canoe with engine counting as perhaps two unpowered canoe units.
These complications (which tend to increase as a greater range of ancillary equipment and of modifications and improvements to the fishing gear come into general use) mean that fishing effort data is often most conveniently collected in two stages. First, a relatively simple measure of total effort, such as number of boats or number of voyages, is obtained perhaps by sampling, often closely linked with the collection of data on total catch. Then detailed information on, for example, the size of boats, the specifications of their gear or other equipment, can be obtained from a section of the fishery to convert the simple measure of fishing effort into the more detailed measure required for the particular user. The detailed information may be collected from a sample of the fishery each year, but sampling can also be done on a time basis; for example the International Commission for the Northwest Atlantic Fisheries collects detailed information (of size of ship, gear, etc.) for all ships operating in its area, but only at intervals of several years.
As in any sampling problem a first essential is to define the population being sampled and to choose an appropriate sampling unit. For this purpose it is nearly always easiest to consider where the fish are landed or first become available for weighing or recording, rather than the position where the actual fishing operations take place. Most simply, the fishery may be based on a number of distinct landing places each of which can be considered as a unit. In a more complex situation landings may take place anywhere along a line - a coastline, or a river, and the natural unit is a certain length of coastline or river. The size of the unit is best taken sufficiently small for one man to cover, preferably in a day, but the limits may be extended when the fishing activity is very sparse. Finally, some, usually primitive, fisheries take place all over an area, e.g. in swamps, or irrigation channels - the fish either being consumed locally or sent to market in small batches. Here the unit may be an area of ground. These types of unit may well be combined, so that a stretch of coast could be divided into a certain number of distinct landing places and lengths of coast between these points.
The first step would be to achieve some stratification, dividing the units (landing places, stretches of coast) according to the order of magnitude of their fisheries. This needs some preliminary survey of the fishery, and, for the fisheries without definite landing places, possibly some geographical survey to delimit precisely the boundaries of the units. Where the division between units may be drawn rather arbitrarily on a stretch of fairly uniform coast it is best to draw the divisions to make the catches in units of the same class as equal as possible. This reduces the within-strata variance to a minimum, and hence increases the precision of any final estimate of total catch, etc. for a given amount of sampling. The division into say, large, medium and small may change through the year for a seasonal fishery, so that a landing place, or stretch of coast, classed as "large" during the main fishing season might be classed as "small" for the rest of the time.
The intensity of sampling would vary according to the importance of the unit. It may be possible to collect complete information from large units, but only sample 1 percent of the small units at one time.
Within a single population unit as so far defined, e.g. a single landing place, further stratifications may be desirable. As suggested earlier, one stratification might be by time. For instance, one length of coast may have been divided into eight units (e.g. landing places), and labor is available to sample about one tenth of the time at each, Then each month's landings at each place could be treated as a separate strata, with landings being sampled on three days of each month. The arrangements of these three days in the month would depend on such circumstances as the ease of travel between places. If this was good, so that there was no difficulty or great expense in recording at point A on Monday, point B on Tuesday, etc., then it would be better to space the three sampling days at roughly ten-day intervals through the month. (Travel between points would also be easier if landings took place only in the morning, leaving the afternoon for possible travel, rather than if landings were made throughout the day.) Conversely, if travel is difficult, the three sampling days may have to be taken together, even if this causes some loss in precision because of the probable correlation between landings on successive days.
A second stratification possible, particularly at the large places, is by class of boat or gear. Even on a day when statistics are being recorded at a landing place it may not be possible to record details of all the landings, and details of catch and effort will have to be obtained from a subsample of the total. The resulting estimate will be more precise if different classes of boat (either in terms of size, or of type of gear used - lines, gill net, etc.) are sampled and analyzed separately. This, of course, requires some record of the total number (including those not sampled for catch, etc.) of each category of boat landing on the day.
Sixteen boats landed at a certain port; catches of two handliners and two gill-net boats were examined; they landed 45 kg, 55 kg, 75 kg and 105 kg of fish respectively. (a) What is the total estimated landings? (b) If it were known that six boats used lines and ten gill nets, what would be a better estimate, 1,120 kg or 1,200 kg?
The quantity of fish in a catch cannot normally be measured directly after they are caught, and the basic statistical data has to be collected at some intermediate point between the fisherman and the consumer. Usually this will be when the fish are landed, often at a market, where they are weighed and sold to, say, a wholesaler. These quantities will not necessarily coincide with the catch, any unmarketable fish (unpopular species, undersized fish, etc.), and also any fish kept by the fisherman for his own consumption being excluded. The possibility of such losses will always have to be examined, and if they might be significant they will have to be estimated by some such sampling scheme, as described below (section 3.1.4). Similarly, if the basic statistics are collected at any stage later than at first landing, intermediate losses have to be estimated.
For instance, in Zambia there is an important fishery on Lake Mweru, with its major market on the Copper Belt, some 250 miles away. Fish sent to this market have to pass a customs post, where a complete record of these exports can be made. Complete records of all fish landed are not so easy to collect, but it is possible, from sample observations, to establish what proportion of the total catch is exported and hence estimate the total catch from the quantity exported.
Conversion factors will also have to be used if the fish are processed in any way before landing, so that the landed weight is different from the weight caught. The commonest example is, of course, gutting and cleaning the fish, where the conversion factor is small and easily determined, but the fish may also be dried or salted before reaching the market. An important special case of the use of such conversion factors is when nominal catch statistics are collected for purposes other than, or by agencies outside fisheries. These are often seriously incomplete, either because inclusion only of particular parts of the catch was intended, e.g. that part marketed, or because of deliberate falsification. A common cause of the latter is the use of returns from the fishermen for tax purposes as well as for the fisheries statistical system. In this case the establishment of a reliable conversion factor (the proportion of the catch not reported to the authorities) may be a matter of some difficulty. It may be better for biological purposes to abandon all use of extensive nominal catch statistics and use completely independent estimates obtained from some sampling system.
Further sampling may be needed to determine the catches within the primary population unit - a landing place, or length of coastline - for the required interval of time - perhaps one day. Sometimes it will be possible to record all the catches being landed. For instance, all the catches may be laid out in boxes for sale by auction, and the quantities easily noted. At other places the sampling unit may cover a considerable length of shore, with perhaps several boats landing at once, and it is impossible to record details of all boats. Hence it will usually be that catches may be estimated from the total number of landings and the catch per landing. This supposes that while recording details of one landing it is possible at least to note how many other boats are landing; in the extreme case even this is not possible, and another step is used, such as estimating the number of landings per hour over part of the day only. Then the recorder would divide the day into one part (say n hours) for recording the total number of landings (say N), and the rest of the day (m hours) for recording details of some of the landings (say k landings) in that period.
Then the average catch per landing = 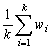 where wi, is the catch of the ith landing whose catch is measured,
where wi, is the catch of the ith landing whose catch is measured,
The allocation of time within the day between recording number of landings and catch per landing depends on the relative variance of the two quantities. Probably the catch per landing is the less variable, and will require less sampling. Landings per hour are more variable, and also are likely to vary systematically through the day. Thus, it is best to spread recording of landing rate throughout the day; a possible pattern is 11/2 hours recording numbers of landings, and 1/2 hour recording quantity per landing repeated through the day.
Once an estimate of the catches at the landing places and days where observations were made is available, the total catches at all landing places and days can be made in several ways. First, if no additional information is available, the sampled places may be assumed to be representative of all places, the recorded catches may be raised by a factor equal to 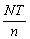 when N is the total number of landing places, T is the number of n days in the period considered, and n is the number of landings - days on which observations were made (n = m x t if observations were made at m places on each type of t days).
when N is the total number of landing places, T is the number of n days in the period considered, and n is the number of landings - days on which observations were made (n = m x t if observations were made at m places on each type of t days).
Sample observations were made at each of six landing places on a stretch of coast on four days during April, and the landings were:
|
(a) |
350, |
480, |
320, |
350 |
kg |
|
(b) |
180, |
170, |
250, |
300 |
kg |
|
(c) |
280, |
310, |
200, |
210 |
kg |
|
(d) |
370, |
230, |
250, |
250 |
kg |
|
(e) |
280, |
350, |
370, |
400 |
kg |
|
(f) |
400, |
430, |
380, |
390 |
kg |
What is the estimate of the total landings along the coast, for the month, given that there are in all 25 landing places
Often additional data available can be obtained on the relative importance of the landing places at which there has been no direct observation of the quantity landed. For instance data on the number of fishermen, or of number of boats may be collected, either specifically as part of the collection of fishery statistics, or for some other reason, e.g. for tax purposes. Such data are likely to refer to a period, the duration as far as possible chosen to give reasonably constant conditions, perhaps for a year in a stable fishery, but monthly or even weekly if the fishery has considerable fluctuations.
Then the data for the landing places where the catches are observed directly will give an average catch per boat (or per man), and this average, multiplied by the total number of boats (or men) for the whole area gives the total catch.
In Example 3.1.3.1 the number of boats at the six sampled landing places was 20, 12, 15, 18, 20, and 25 respectively. At the other nineteen landing places there were, as counted at the beginning of the month, 250 boats. What is the estimate of the total catch, using the additional information on numbers of boats (catch per boat per day =  = 17.045 kg total catch = 17.045 x 360 x 30 = 184,086 kg)?
= 17.045 kg total catch = 17.045 x 360 x 30 = 184,086 kg)?
Note that this is lower than the previous estimate, because the average number of boats at the sampled landing places is greater than elsewhere. This could well arise in practice when a proper system of random sampling is not used, as it may well be more convenient to base recorders at the larger landing places.
Statistics of catches and landings are often treated as being synonymous (apart from the need of converting landed weight of gutted or salted fish to weight, as caught, of whole live fish). Often, particularly in northern Europe and America, there is considerable rejection by fishermen at sea of both unwanted species and unwanted (usually small) specimens of commercially valuable species. Observations on shore, such as those described in the previous section, will only provide data on the quantity landed. For some purposes, particularly when assessing the effect that the fishery is having on the stock, data on catches are required. (Generally it may be assumed that fish caught but discarded will be dead, and therefore removed from the stock. If some fish may survive, then the significant quantity is the quantity of discarded fish that die; estimating the proportion of discards that die will require a further collection of data, e.g. by observers on commercial ships or special experiments.)
Only someone at sea on the fishing vessel will be aware of how much fish is rejected, but generally fishermen will be too busy to keep regular records of the quantity rejected. Thus complete statistics of quantities rejected are very unlikely to be obtained, and if obtained are likely to be inaccurate. A sampling survey, either by sending special observers on fishing boats, or by obtaining special co-operation of a sample of the fishermen, is probably necessary if it is likely that any appreciable quantity is being rejected. Fishermen may well be prepared to keep accurate records of fish rejected on, say, one trip in twenty although they would not do so on every trip. Special observers sent out on board commercial vessels at sea will secure accurate data on the quantity and type of fish rejected. However, they will often be inefficient, in the sense that the ship they are on may continue to fish in one fishing ground for some time, with the same proportion being rejected, this proportion being different from that on other grounds. Thus the variance of the estimate of the average proportion rejected in the whole fishery will be rather high relative to the time spent recording rejection. If the special observer can also carry out additional observations, such as examination of the catch for size, maturity, feeding, etc., then wasteful repetition of similar records of quantity rejected may be eliminated, and the quantity rejected may be estimated accurately and efficiently.
The proportion rejected usually varies very markedly both with season and fishing ground, so that stratification is desirable. Within one strata, i.e. on the same ground during one season, the proportion rejected is likely to be fairly constant, through possibly varying from one year to the next, e.g. being large when a strong year-class is just below commercial size. Thus the accuracy obtained is likely to be high, even with very few samples - half-dozen samples within each strata should give estimates of serviceable accuracy. As usual the intensity of sampling should be governed by the expected quantity rejected. In the extreme case there may be certain seasons or grounds, particularly spawning grounds, which are known to have negligible, or no, rejection and thus may be omitted from the sampling system, permitting a greater intensity of sampling at other seasons or grounds.
During four voyages in the summer five tons of small fish were observed to be discarded, and forty tons landed; during a simple voyage in the winter only 0.1 tons were discarded, and eleven tons landed. What is the estimated weight discarded by the whole fishery if the total landings were 4,000 tons in the summer and 5,500 tons in the winter (500 + 50 = 550 tons)?
If the information is obtained from fishermen's records rather than by special observers, two procedures are possible: either to obtain a sample of fishermen who would give complete information from all, or most, of their trips, or to get information from all fishermen, but each one only providing information from a small fraction of his trips.
The first system, while probably much the easiest to operate, would have the drawback of being in no way a random sample, including only the more co-operative fishermen. For instance, it is likely that the fishermen who use small mesh or blinded nets (and thus catching a high proportion of small fish) would be less likely to be included. Thus the sampling would be biased and the estimates of the proportion rejected would be too low. Before accepting as unbiased the estimate obtained from the data received, it is important that some check be made on how the average rejection might deviate from that of the sampled boats, e.g. by considering the abundance of the smallest sizes of fish landed, etc.
A problem rather similar to that of rejection is that of the processing, e.g. of fish meal at sea, where it is impossible to determine the composition of the catch by species by any examination when the catch is landed. Again, as in rejection, the more important problem is to determine the quantity of the small undersized specimens of the commercially valuable species processed, rather than of all species.
Data may be collected either by special observers, or from records of fishermen. The proportion of each important species may probably most conveniently be collected relative to the quantity processed (as this total will be known from landing records), rather than to the total catch.
Simple effort statistics, for instance in the form of number of fishermen, or number of boats, are rather easy to collect, usually without a sampling system and in fact can be used (as in section 3.1.3) as an intermediate stage in estimating the total catch. Such statistics, however, are unlikely to be good enough - i.e. closely enough related to the real intensity of fishing on the stock or stocks - for all biological purposes, particularly in any developing fishery. More sophisticated measures of fishing effort are likely to be needed, involving fairly precise measures of the time spent fishing, the size of boat, number of size of nets, etc.
The most suitable units of effort, in the biological sense, may not even be known at the time the statistical data are being collected. Thus, for a shoaling pelagic fish such as the anchovy, the catch per haul of a purse seine is probably, if corrected to a standard size of net, a good measure of the density, or size, of the individual shoal on which the net was shot. The actual abundance of the entire stock may, however, be more closely related to the number of shoals, or the distance between them, than to the size of the individual shoals, which may remain much the same size for a range of stock abundance. The number of shoals will be estimated from the time which has to be spent by the fishermen looking for fish before shooting the net. Corrections will have to be made for any devices which help the fishermen to find the fish more quickly, e.g. quicker vessels, radio communication between vessels, echo sounders, etc. The resulting expression for the estimated index of stock density, in effect the catch per unit corrected effort, will be a possibly complicated combination of searching time and catch per haul, and one whose form may well be repeatedly revised on the basis of further research. However, the problem is a reasonably straightforward problem of fishery research, provided all the relevant data have been collected.
Most of the detailed information would be collected by some sampling method. Thus full information might be collected on the number of landings - though this itself might be obtained by another sampling system, as described for catch statistics earlier. From a proportion of the landings, say one landing in seven - perhaps from all boats landing on one day each week, fuller information is collected, say on total time away from harbor, divided into time steaming to the fishing grounds, time searching for fish and actual fishing time, and on the number of hauls made - perhaps distinguishing successful hauls, and those in which no fish were caught. Information could also be collected during these sample interviews on such things as size of net, radio and echo-sounding equipment, etc. These, however, will not change, except very occasionally, and more accurate information would be obtained by complete surveys, at intervals - possibly this would be combined with annual registration, etc.
3.2.1 Methods of measuring and recording
3.2.2 Selection of the sample
3.2.3 The time and place to sample commercial catches
3.2.4 Stratification
3.2.5 Size of sample
3.2.6 Raising factors
Of all sampling work carried out by fishery research workers, the most extensive is almost certainly that concerned with determining the size and age composition of the catches. It is useful to distinguish two types of sampling program (though as in most classifications the dividing line is not exact). First there is the thorough and precise examination and measurement, often of several characteristics (e.g. total length, fork length, weight, gonad weight, maturity age, etc.), but of relatively few specimens. This sampling is usually done under laboratory conditions. Secondly there is the sampling for a single rapidly determined measure (e.g. total length) for a large number of specimens, often under the rather uncomfortable conditions of fish markets.
So far as the first type of sampling is directed at determining racial or specific differences, e.g. in the ratio of two body dimensions, or in mean vertebra number, the sampling problem is small. The precision achieved is determined almost entirely by the number of specimens examined, regardless of the method of collection. Tests of significance between sets of samples will determine whether sufficiently large samples are being taken for the purposes required, either of showing that certain groups of fish are distinct or that possible differences within a group are less than a certain limit.
Slow and detail sampling is also used to estimate directly the composition of the commercial catches by age, maturity, etc. This direct sampling will most often be a very inefficient sampling method, a much more preferable procedure being to relate these quantities to length by a relatively small key sample, and hence estimate their frequency in the catches as a whole from relatively extensive length measurements. Most sampling is likely therefore to consist of numerous length measurements, for which suitable techniques both in statistical design and in manipulation can achieve great improvements in efficiency. Though the manipulations concerned are also discussed in another manual in this series (another good discussion is given in the report of the FAO International Training Centre on the Methodology and Techniques of Research on Mackerel (Rastrelliger), Bangkok, 1958), it is appropriate to give some short discussion of the problem here. The main questions to be settled are, measure to be used (total length or fork length, etc.), precision of recording (as millimeters or coarser grouping) and measuring device (measuring board, etc.). As all measures of length are extremely closely related to each other, and to other measures of "size" (weight, etc.), the one to be adopted should be that which permits the most rapid and accurate measurements to be made under the often rather difficult conditions of market and easily determined. The actual choice will depend on the species of fish concerned; most often the total length will be best, but if the tail has a well-marked fork, length to the angle of the fork (fork - length) may be more suitable. A minor question is what to do about fish which have been so damaged as to make the length used indeterminate (e.g. badly frayed tail). These fish might simply be omitted from the sample, but it is not unlikely that damage is correlated with size, bigger fish being more liable to damage. A mission could therefore give a biased result, toward underestimating the abundance of large fish, and a better procedure is to estimate the size, which is most readily done by comparison with undamaged fish of about the same size.
In an earlier section it was mentioned that in studying frequency distribution, of length or any other quantity, extreme precision, i.e. a large number of length groups, was not desirable, being extremely cumbersome to analyze. It has also been shown (e.g. Holt, 1958) that in attempting greater precision, the accuracy actually achieved can decrease, thus in measuring lengths to the millimeter, concentration on the last figure on the scale can cause the centimeters to be misread (183 mm read as 173). Similarly when plaice have been marked under rather difficult conditions it is not usual to find they have apparently grown (or shrunk) exactly 10 cm in a few days (though changes of say, 7 or 13 cm are very rare). As a rough guide 15-25 effective groups have been suggested (Yule and Kendall, 1950) with perhaps more where data are very abundant, or the frequency distribution complex. Thus the grouping suggested for Rastrelliger, whose lengths in the catches run from around 13 cm to 22 cm, is half-centimeters, giving 18 groups, while the standard for cod in the Northwest Atlantic, which range from 40 to 130 cm is 3 cm, giving about 30 groups (this latter is perhaps too fine a grouping). The markings on the measuring board will be determined by the groupings used. If 1-cm groups are used, the 1-cm markings should be made clear and distinct, and not confused by the addition of 1/2-centimeter or millimeter markings.
The simplest method of recording is for one man to do all the handling and measuring of the fish, while a second man records the lengths on a suitable form. The design of this form will be discussed in more detail in a later section, when the additional information needed, other than purely the number at each length, will be discussed. In some forms the lengths are written down in serial order as the fish are measured, being retabulated as a frequency distribution later. This is convenient in detailed sampling, where several attributes - length, weight, maturity, etc. - are being recorded for the same fish, but normally it is much better to record in a manner that produces a frequency distribution immediately. This may be done by having a form printed with the possible range of lengths down one side. As each fish is measured a mark is made against the appropriate length on the form, and the number at each length can be simply totaled when the sample is finished. Totaling is easier if the marks are arranged in a system, e.g. by grouping the marks in fives - four vertical and the fifth diagonally across them, or better, the first four as sides of a square, the fifth as the diagonal (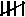 or
or  ). As this system requires two men at the sampling place, it may be wasteful of manpower when sampling is done at a distance from headquarters, though the second man is often useful in helping move boxes of fish, etc. A direct modification is for the measurer to talk into a small tape recorder; the tape can then be played back when convenient and the measuring form made out in the normal fashion. Though the actual time involved is the same, the form can be made out at any time, rather than very early in the morning. This system is being used in several European countries.
). As this system requires two men at the sampling place, it may be wasteful of manpower when sampling is done at a distance from headquarters, though the second man is often useful in helping move boxes of fish, etc. A direct modification is for the measurer to talk into a small tape recorder; the tape can then be played back when convenient and the measuring form made out in the normal fashion. Though the actual time involved is the same, the form can be made out at any time, rather than very early in the morning. This system is being used in several European countries.
A simpler method by which one man can produce a permanent record is to use plastic or celluloid strips. These are placed on the board, one strip being used for each sample. No specific measurements are made while handling the fish, but a hole is punched in the strip at the end of the tail (or for whatever measure of length is being used). On return to the laboratory the strip is replaced on a measuring board, and the number of fish at in-length interval is at once given by the number of holes in that interval. A somewhat similar system is to use a type of plastic on which pencil marks will not rub off too easily. The measuring board is covered with this plastic, and the length intervals marked permanently on it. A pencil mark is made in the interval in which the end of the tail (or fork, if appropriate) falls, grouping into fives as before if necessary. This, like the punching of the hole for the previous method, can be done with very little delay in handling the fish. At the end of each sample the numbers in each group can be totaled, and entered on the suitable form.
When the fish are lying in a large heap, perhaps of several hundreds, or even more - for instance herring on the deck of a research vessel - from which only a proportion are taken and measured, the wrong method of selection can give rise to serious bias. Most people tend to take first the larger and more obvious fish. A sample taken without care is therefore likely to be seriously biased; a nominally "random" sample of cod taken for age determination on board the English research vessel Ernest Holt had an average length more than 10 cm greater than the catch as a whole. Even if the sampler is aware of this bias, it cannot be eliminated with certainty, and the chance of overcorrection - picking too many small fish - is introduced. The danger of bias is most directly eliminated by measuring all the fish in the heap, and if this is reasonably practicable it should be done, even if the sample size would then be rather larger than would otherwise be desirable. If the complete heap is too large, the number to be measured may be reduced by measuring only a part, e.g. one fifth of the total. This may be done by picking up all the fish, and separating them into five lots, e.g. five baskets, one of which is then chosen at random and the fish in it measured. The fish should be allocated to each group a few at a time, so that each group contains some of the fish picked up first (probably larger than average), and some of those picked up last (smaller than average). It is probable, though, that some groups will still have more than their fair share of big fish, and an improved degree of mixing may be achieved by repeating the process. That is, all the fish can be reallocated, a few at a time, to five new groups.
Alternatively the sample to be measured may be determined by its position, all the fish on one side being sampled. It is important that all the fish in the section are measured, the area sampled being cleared right down to deck level. Bias is still possible, the larger fish being more likely to be in one part of the catch than another, and this can in part be corrected by sampling different parts of the catch at different times; one haul the after end is sampled, the next haul the forward end.
Commercial catches of any quantity are normally placed in boxes, baskets or similar containers, and often one or more complete boxes will form a convenient size of sample. Here there is no risk of bias through picking up the larger fish first. If a complete box is too large a sample and only part of the fish are measured then precaution must be taken against introducing this bias. As before this may be done either by handling all the fish, separating them, a few at a time, into two or more groups, or by taking all the fish at, say, the left-hand side of the box, from the top right down to the bottom.
Great care is necessary to ensure that the system used in choosing the time and place to take samples will give unbiased estimates of the commercial catches. Large systematic differences are likely to exist not only between fish caught at different places or with different gear, but also, after landing, between fish sent to different markets, or used for different types of processing. Most biologists are fully aware of the former chances of bias, but the latter may well be unsuspected, and give rise to serious bias.
For instance, an apparently convenient method of obtaining a sample is to arrange for a particular fish merchant to send a random sample of fish to the laboratory. This merchant may be accustomed to buying a particular size or condition of fish for his own market, e.g. large fish so that the sample would be biased toward the larger sizes, while there is the added risk that the fish sent to the laboratory will be the cheapest size or condition. Sampling, therefore, should be carried out as soon as possible after the fish are caught, before any bias is introduced which cannot be corrected. This, of course, also means that it will be easier to determine where, when, and by what gear the catch has been made.
Ideally, then, sampling of commercial catches will be done actually on board during the fishing operation. It may be difficult in practice to send scientists on board, and to do so will often be inefficient. That is, the scientist will have to remain on board the whole trip, perhaps several days, during which fishing may be done only on one or two grounds, so that in a week he may effectively take only a couple of samples. In rather less time a scientist ashore can take samples from perhaps twenty or thirty boats as they land, getting information from a corresponding variety of grounds, and, perhaps, gear. This inefficient use of scientists' time will be greatly reduced if the scientist can also take other observations on the research vessel, e.g. on the quantities of small and unmarketable fish rejected, the feeding of the fish, possibly weather and hydrographic observations, etc. While such observations are not strictly part of the sampling problem discussed here they may be integral parts of a complete research program. Consideration of them is vital in determining whether or not sending observers on commercial vessels is worth while in terms of economical use of manpower.
If observers can transfer at sea from one ship to another, then the number of samples that can be taken per month, or per day will be increased, and with them the general efficiency of the sampling method. For instance, it would be possible in the purse-seine fishery of the Gulf of Siam for observers in a small boat to go among the fleet each night, board a vessel when it has made a catch, and measure a sample of fish noting the time, vessel and exact place of capture, all in a very short time.
This could be repeated several times, so that perhaps a dozen samples, from accurately known positions and times, could be made in a single night.
For most fisheries the most suitable opportunity for sampling is directly after the fish are landed. Some markets, e.g. in England or Japan, provide the most favorable conditions. Here the fish are landed during the night and are sold by auction in the morning. There may be an interval of an hour or more after the complete catch has been landed and laid out in the market when the men landing the fish have left, and before the majority of the fish merchants have arrived for the sale offish, during which the catch can be very easily sampled without disturbance between the scientists and the fish merchants. In such conditions the techniques of measuring, in terms of time and space needed, are not critical, but elsewhere both in England and other countries, the period of calm may be small or nonexistent, the fish being landed and sold without delay. Even so, there are nearly always a few minutes during which any particular basket of fish is available for sampling, provided the scientists are able to work quickly and in distinctly difficult conditions, and provided there are reasonably good relations between the scientists and the other people in the market. These last two requirements may sometimes be conveniently met by a small payment to the fisherman for measuring his catch. This is likely to be most suitable in a fishery consisting of a large number of small fishermen each landing only a small catch, and for which a convenient sample might be the entire catch of one fisherman.
Sampling at the place of first landing may be difficult or impossible, for instance, because the necessary staff cannot get to the landing place at the right time. Sampling will therefore have to be at the first convenient stage in the chain of distribution, e.g. at the wholesale market. The further the sampling is removed from the actual time of capture, the greater is the difficulty in determining the details of capture (especially the position and gear) so that valuable biological information is likely to be lost. If all the catch does not go through the same channels - for instance, some goes to the wholesale markets for sale as fresh fish but the rest is sent for salting - and regular sampling can only be conveniently done at, say, the wholesale market, then the fish sent for salting have no chance of appearing in the samples. Thus the sampling system cannot give a random sample of the catch, and periodic checks must be made of the composition of that part of the landings which is not regularly sampled to ensure that it does not differ from the rest of the landings. For instance, fish used for the production of fish sauce are likely to be smaller than those used as whole fish. If such differences do exist unbiased estimates of the catches can be obtained only by sampling all the channels of distribution or, better, overcoming the difficulties and sampling the fish when first landed.
Example 3.2.4.1
Example 3.2.4.2
Example 3.2.4.3
Example 3.2.4.4
Example 3.2.4.5
An ultimate object of sampling may be to determine the composition of the total catches of a certain species for a complete year. A year is too large a unit to be sampled as a whole, and some degree of division, or stratification is necessary for practical reasons, as well as to increase the efficiency of sampling. Likely divisons are by season or time of landing, place of landing, or method of capture. Thus a particular division could be the landings during August, on a particular stretch of coast, by vessels using gill nets. From all the fish landed at this time and place one or more samples will be taken, and the composition of these landings estimated; similarly the landings at other times, at other places and by other gear (if any) are sampled and their composition estimated, and hence by addition the composition of the total landings obtained. A vital part is the knowledge of the magnitude of the catches in each division, so that the correct "raising factors" can be used. The raising factor is the factor by which the numbers in the sample have to be multiplied to give the total numbers in the population sampled.
Samples of Hilsa, each of 50 kg, were taken during 4 winter months. The length composition of each sample is given below:
|
Length (mm) |
Dec. |
Jan. |
Jan. |
Feb. |
Mar. |
|
255- |
18 |
7 |
4 |
2 |
3 |
|
275- |
16 |
9 |
6 |
4 |
2 |
|
295- |
18 |
11 |
12 |
3 |
4 |
|
315- |
10 |
14 |
16 |
9 |
6 |
|
335- |
7 |
10 |
19 |
12 |
11 |
|
355- |
6 |
9 |
15 |
16 |
10 |
|
375- |
5 |
12 |
11 |
8 |
14 |
|
395- |
|
6 |
5 |
12 |
8 |
|
415- |
|
|
8 |
7 |
4 |
|
435- |
|
|
|
3 |
2 |
|
455- |
|
|
|
|
6 |
|
TOTAL |
80 |
78 |
96 |
76 |
70 |
The notation 255- used for the length groups means that the group includes fish of from 255 mm inclusive up to, but excluding, 275 mm.
The total weight landed in each month was 250 kg in December, 1,000 in January, 2,500 in February and 500 in March.
Determine the total numbers landed in each length group, and also the percentage length composition of the total landings. Compare the latter with the percentage length composition of the 400 fish measured.
The raising factors for each month are 250/50 = 5, 1,000/100 = 10, 2,500/50 = 50 and 500/50 = 10. (Note that two samples were taken in January, so they are added together before raising; the raising factor is, of course, half what it would be if only one sample had been taken.) Using the appropriate raising factor for each month and adding up, the length composition of the total landings is obtained, as follows:
|
Numbers landed |
Numbers measured |
|||||||
|
Length |
Dec. |
Jan. |
Feb. |
Mar. |
Total |
% |
Total |
% |
|
255 |
90 |
110 |
100 |
30 |
330 |
5 |
34 |
8.5 |
|
275 |
80 |
150 |
200 |
20 |
450 |
7 |
37 |
9 |
|
295 |
90 |
230 |
150 |
40 |
510 |
8 |
48 |
12 |
|
315 |
50 |
300 |
450 |
60 |
860 |
13 |
55 |
14 |
|
335 |
35 |
290 |
600 |
110 |
1035 |
16 |
59 |
15 |
|
355 |
30 |
240 |
800 |
100 |
1170 |
18 |
56 |
14 |
|
375 |
25 |
230 |
400 |
140 |
795 |
12 |
50 |
12.5 |
|
395 |
|
110 |
600 |
80 |
790 |
12 |
31 |
8 |
|
415 |
|
80 |
350 |
40 |
470 |
7 |
19 |
5 |
|
435 |
|
|
150 |
20 |
170 |
3 |
5 |
1 |
|
455 |
|
|
|
60 |
60 |
1 |
6 |
1.5 |
|
TOTAL |
400 |
1740 |
3800 |
700 |
6640 |
|
400 |
|
It may be noticed that the smaller fish are considerably overrepresented in the samples. This is because the sampling is spread fairly evenly through the season, while the landings are greatest in February, when the larger fish predominate.
In calculating the raising factors the quantity being estimated must be clearly kept in mind. In the example above the quantity to be estimated is the numbers landed in each size group, and the raising factors are determined by the quantity landed each month. Quite different raising factors will be used if estimates are to be made of the average size-composition of the stock over the period considered. The raising factors for each month will be given by the size of the population, which will have to be estimated in some way.
If in Example 3.2.4.1 it is assumed that the sizes of the population in December, January, February and March were proportional to 2:3:3:2 respectively, calculate the average length composition of the stock.
The main problem to be faced in the stratification of the landings is the amount of subdivision to be done. For the application of the usual methods of stratified sampling, the divisions must be few enough for samples to be taken from each division; small and numerous divisions are desirable if there are great differences between divisions, and large and few divisions if the composition of possible divisions are similar. Each division must be such that it is possible to take samples from it. The number of samples taken from any division should be, as far as possible, proportional to the variance in that division.
There is no need for all divisions to be of the same size. Consider divisions in time for example, in a fishery which, though continuing throughout the year, has peak landings in a short season. In this main season, a week may be considered as a suitable division, samples being taken, say, daily, and in the off-season each month may be considered as a unit, with samples taken weekly.
The monthly catches of mullet (Mugil spp.) from Lake Menzala, Egypt, in 1956-57 are given in the table below (data from Panse and Sastry, 1958):
|
Month |
June |
July |
Aug. |
Sep. |
Oct. |
Nov. |
Dec. |
Jan. |
Feb. |
Mar. |
Apr. |
May |
Total |
|
Catch (tons) |
136 |
166 |
343 |
372 |
523 |
395 |
264 |
235 |
140 |
98 |
117 |
75 |
2864 |
If time and labor are available to take 10 samples during the year, suggest how they should be allocated.
It is not possible to say that any particular allocation is the "right" one, but a reasonable one would be to have five divisions, with two samples taken in each period; without knowledge of the size distribution in each month, it may be assumed that the variance of the length distribution is the same for each period - so that the periods should be chosen to make the weight landed in each period as far as possible the same, i.e., close to the average of 580 tons. If the sampling period starts in January, a possible division would be January-April, May-July, August-September, October, November-December.
Suppose that in a fishery with a similar seasonal distribution of total catch, it was known from earlier sampling that the main size groups caught in each month were as follows:
|
Month |
June |
July |
Aug. |
Sept. |
Oct. |
Nov. |
Dec. |
Jan. |
Feb. |
Mar. |
Apr. |
May |
|
Sizes |
19-21 |
20-22 |
21-24 |
22-25 |
23-25 |
24-27 |
20-28 |
20-28 |
15-28 |
15-18 |
15-18 |
16-20 |
How would this additional information alter the division into periods suggested above?
It appears that for most months only one major size-group is present, except in the period December-February; most intensive sampling is necessary in this period. The rate of change of size is slowest in the peak fishing season (September-October) so relatively less sampling is necessary then. A suggested division into five periods is, therefore, January-February; March-May; June-September; October-November; December.
When dividing the total landings into ports or stretches of coast, the physical ease of sampling is important. The laboratory, or normal place of work of those who will do the sampling, is likely to be at or near an important landing place. Sampling at this place can therefore be done with little waste of time; perhaps two hours work actually sampling can be done at the expense of three hours away from the laboratory. Sampling elsewhere may mean the loss of a complete day's work or more. Information must, however, be obtained at these more distant landing places if a reliable estimate of the composition of the total landings is to be obtained. In some circumstances it may be possible to confine research to the fish landed at the most convenient place, regarding the stock of fish represented in these landings as a sample of the stock or stocks of fish exploited by the fishermen of the whole area. This may well occur when investigating an inshore species, where each stretch of coast may contain separate and discrete stocks. Reliable results are not likely to be obtained if the stock is exploited by various groups of fishermen and samples are only obtained from one group. Before arranging a complete regular sampling program for the whole region, a preliminary survey should be made of the composition of the catches at each place. It may happen that there is no appreciable difference from place to place and regular sampling can be carried out where most convenient, subject to occasional checks elsewhere to make sure that the composition continues to be the same as at the main sampling area. A special case of this may occur in offshore fisheries. The total landings at two ports may differ in composition because the main fishing areas of the two fleets differ, but overlap. Thus the landings may be divided according to area fished and all samples taken at one port, but weighted according to the total landings from each area to give unbiased estimates of the total landings. Again, periodic checks are necessary to confirm that the catches from any particular area made by fishermen from different landing places do have the same composition.
Often, though, there is no alternative to including all major landing places in the regular sampling program. The division of the total into areas, and the choice of size of sample taken from each division are then carried out in the normal manner with one modification. Normally the best size of sample taken from any division is proportional to the size and variability within that division. This is true so long as the cost (in time and labor) of taking a sample of a given size is the same for all divisions (in this case, areas). If, in fact, the cost varies from area to area, then this has to be taken into account, more samples being taken in the areas where sampling is easiest and cheapest. In fact, the best size of sample in any area will be inversely proportional to the cost of taking a sample of unit size in that area. In mathematical terms the best size of sample, n, in a particular division will be given by
n � Ns2 (equal costs in all divisions)
and n � Ns2/C (variable costs)
where
C is the cost of a sample of unit size in the divisionN is the total landings in the division
s2 is the variance within the division.
As before it is not essential to obtain samples of exactly the right size, but it is important to take cost into account, and also not to do all sampling in the easiest place.
Stratification, or division, by method of capture is often most important, both in understanding the fishery and in obtaining the best estimate. There is often a considerable difference in sizes of fish caught by different gear, making division desirable. Also, one gear may take a wider range of sizes than the other, thus requiring more intensive sampling.
The percentage length composition of cod landed at Grimsby in 1957 caught by trawl and Danish seine respectively were:
|
Length (cm) |
30-39 |
40-49 |
50-59 |
60-69 |
70-79 |
80-89 |
90-99 |
100-109 |
110+ |
|
Trawl |
26.3 |
38.8 |
19.0 |
7.9 |
3.7 |
1.9 |
1.7 |
0.6 |
0.1 |
|
Seine |
0.6 |
13.3 |
16.0 |
8.3 |
6.8 |
15.0 |
28.0 |
10.5 |
1.5 |
The total landings were 4,500 tons by trawlers and 3,500 tons by seiners. Calculate the variance of the mean length of fish caught by each type of gear, and discuss the allocation of sampling effort between the two gear:
|
Trawl: |
mean = 49 cm |
variance =194 cm2 |
|
Seine: |
mean = 78 cm |
variance = 440 cm2 |
The size of sample giving the best estimate of the total mean length from the two gear, as judged by the weight landed, and the variance of the mean lengths should be in the ratio 45 x 194:35 x 440, i.e. about 1:1.7.
If, in fact, the samples taken were of 1,500 fish weighing 1.9 tons from trawl-caught fish, and 500 fish weighing 2.2 tons from seine-caught fish (these samples, by weight, are in the ratio 1.9:2.2 = 1:1.2, which is reasonably close to the best distribution, though rather more seine-caught samples would be desirable), calculate the total numbers at length sampled from trawl and seine, and hence, using the correct rasing factor, the total numbers landed in each 10-cm group.
The greatest benefit from stratification can be obtained when the fish are divided into different size categories. At the extreme, where such sorting is very detailed and consistent, information on the total quantities landed in each category will be almost sufficient to determine the total size composition. However, advantages from sorting into size categories can still be gained whenever the total landings are divided into classes which differ markedly in size composition, even when the division is not very precise. So long as the total landings can be divided at all into, say two categories, large and small, then the condition that stratified sampling is advantageous is satisfied - there is a bigger (probably much bigger) difference in size composition between categories than there is within a category.
Of course, each category must always be sampled separately when sampling the fish landed by one ship, but there is a question whether or not to consider categories when estimating the composition of the total landings. The two procedures may be illustrated by an example.
Plaice landed at Lowestoft are normally sorted into four categories - large, medium, small and thin, the last being poor quality fish of lesser market value. During a certain period the total quantities of fish landed were: large, 4,500 kilograms; medium, 9,000 kilograms; small, 23,040 kilograms; and thin, 660 kilograms - a total of 37,200 kilograms. A certain ship landed 180, 600, 2,080 and 60 kilograms of each category and of these, 60, 30, 18 and 60 kilograms were measured, giving the following length composition:
|
Length group (cm) |
25-29 |
30-34 |
35-39 |
40-44 |
45-49 |
50 + |
Total |
|
Large |
|
|
|
16 |
33 |
15 |
64 |
|
Medium |
|
2 |
47 |
27 |
|
|
76 |
|
Small |
26 |
41 |
8 |
|
|
|
75 |
|
Thin |
|
|
7 |
15 |
14 |
14 |
50 |
(a) estimate the numbers in each length group in each category landed by the sampled ship;
(b) estimate the total numbers landed in each length group, (i) by raising each category separately to the total landings (stratified), or (ii) by raising the total landings of the sampled ship, of all categories;
(c) comment on the relative numbers sampled in each category.
The raising factors for estimating the total landings by the sampled ship are, for each category, 3, 20, 160 and 1 respectively, giving the estimated size composition, the total being obtained by addition.
|
Length group |
25-29 |
30-34 |
35-39 |
40-44 |
45-49 |
50 + |
Total |
|
Large |
|
|
|
48 |
99 |
45 |
192 |
|
Medium |
|
40 |
940 |
540 |
|
|
1520 |
|
Small |
4160 |
6560 |
1280 |
|
|
|
12000 |
|
Thin |
|
|
7 |
15 |
14 |
14 |
50 |
|
TOTAL |
4160 |
6600 |
2227 |
603 |
113 |
59 |
13762 |
To estimate the total landings by all ships, using the data on the quantity landed of each category, the raising factors of 25, 15, 8 and 11 for each category respectively are used.
|
Length group |
25-29 |
30-34 |
35-39 |
40-44 |
45-49 |
50 + |
Total |
|
Large |
|
|
|
1200 |
2475 |
1125 |
4800 |
|
Medium |
|
600 |
14100 |
8100 |
|
|
22800 |
|
Small |
33280 |
52480 |
10240 |
|
|
|
96000 |
|
Thin |
|
|
77 |
165 |
154 |
154 |
550 |
|
TOTAL |
33280 |
53080 |
24417 |
9465 |
2629 |
1279 |
124150 |
Another estimate can be obtained by raising the total of the sampled ship by the factor 6,200/620 = 10, giving the estimate
|
Total: |
41,600 |
66,000 |
22,270 |
6,030 |
1,130 |
590 |
137,620 |
The second estimate gives more small fish (under 35 cm) and less (and for some sizes considerably less) large fish. This is because the sampled ship landed proportionately more of the category small compared with the total landings, though neither estimate can be considered as definitely right (or wrong). The first one, which takes into account the quantity of each category landed by all ships uses some information on the sizes of fish landed by the ships which were not sampled and is therefore likely to be closer to the actual value.
The basic sampling unit is likely to be the catch (or more usually landings) by one ship or one unit of gear. The choice in size of sample therefore lies between measuring a large number of fish from one ship, and a smaller number from each of several ships. Sometimes the practical situation will limit the size of sample; if the fish are being sold, or moved away almost as soon as they are landed, it may be possible for a single box to be measured without disturbance where a larger sample would cause undue interruption to the fishermen's activities. This underlines the fact that good market sampling - and hence proper estimates of what sizes of fish are landed, and are in the sea - depends as much on the ability of the men doing the measuring (either singly, using "one-man" boards, or in pairs, one measuring, one recording) to work in often difficult conditions and maintain friendly relations with the fishermen, as on the statistical design of the sampling system.
Assuming a choice in size of sample, this will as usual be governed by the variances between and within units (ships, etc.) and by the time spent measuring fish and moving between ships. The variance between ships is usually more than the variance within ships, especially when all the fish landed by a particular ship come from the same ground, or have been caught in the same haul (e.g. of a purse seine). Movement from one ship to another to take samples is likely to be easy when catches are landed at the same time - e.g. just before the morning's auction sales. In these conditions small samples, and many of them, will be the best system. At other places ships may land at intervals during the day, so that a second ship's fish may not be available for sampling directly after finishing measuring from the first ship. Here larger, but fewer, samples will be better.
In Example 2.4.3 data of some herring measurements were examined in some detail, and it was shown that, for a given time spent sampling, the mean length of herring was estimated with least variance if samples of 17 fish were taken. Before taking this analysis, or similar analyses for other situations, as measures of the best size of sample, two points must be noted. First, and most important, is that with such a small sample size, the problem of unconscious selection by the man measuring the fish may become critical (cf. Example 3.2.4.2). If, as is usual, the fish are landed in baskets or boxes a sample size of a complete box or boxes is best, unless this is much bigger than the indicated optimum size. In the latter situation at least enough fish should be measured to reduce the possibility of bias - e.g. half a box, measuring all the fish from one side. Secondly, length measurements are used and interpreted in many ways, and it does not follow that the sampling system which is most efficient in estimating the mean length of fish landed is also the most efficient in estimating other quantities, e.g. proportion of fish above a given size, or, in combination with a fixed amount of age data, mortality. However, the optimum size of sample is not likely to be very different, and mean length and its variance, being about the easiest to calculate, give as good a guide as any.
At a certain market it takes half a minute to measure a shark; ships land their catches close together, so that it takes only a minute between finishing measuring the catch of one ship and starting measuring on the next. Assuming the same ratio of variances between and within ships as in Example 2.4.1, what is the nominal optimum sample size (three fish)?
How would the optimum sample size in both examples be changed if landings were infrequent, so that to sample a ship's landing required a special visit to the fish market, taking approximately one hour (60 fish, 20 fish)?
So far the choice of sample size has only been considered for the simple situation where the landings by one ship are essentially homogeneous. Some slight modifications are needed if the landings have been sorted into two or more categories, based on size or condition of fish.
If the sorting is consistent - the same categories used for each landing - then each category could be treated entirely independently. For each category there is an optimum size of sample, and the division of the total sampling effort between categories will be made on the usual criteria of stratified sampling - more samples from the bigger or more variable strata. This will usually mean that the optimum number of samples is different for different categories, and while there is no overriding necessity to do so, it is more convenient when sampling from a ship to sample from all categories, i.e. the number of samples is the same for all categories. This will mean some compromise is necessary, so that for categories where an above average number of samples would have been desirable, the size of sample is increased (e.g. instead of measuring one box of large fish, two boxes are measured). It may be emphasized that the fact that the optimum size of sample is small implies nothing about how much sampling is desirable, but merely that the sampling effort is best directed toward increasing the number of samples.
The use of raising factors has been mentioned in passing in earlier sections. In one form or other they are a vital step in combining and analyzing sample data, and one whose importance is easily overlooked. Unless the sampling system used is very simple, the length-distribution of the fish measured will be different, and perhaps markedly different, from the estimated length-distribution of the "population" being sampled - the population in this sense being possibly all fish of the given species landed during the year, or perhaps all those above a given size in the area being fished. When more than one sample has been taken from a population, each giving an estimate of the size distribution of the population, the estimate obtained from the combined samples may depend as much on the raising or weighting factors used as on the actual distributions of each sample. An extreme example is when the fish are sorted into fairly precise size categories. Then the most important information about the size-distribution of fish in the landing as a whole is the record of the quantities landed of each category. More than one set of raising factors may be used, each set being followed by a summation of separate individual raised samples or groups of samples; such a series of operations might be:
1. Measure a box of fish from a particular boat at a particular landing place, in a particular month.
2. Raise the sample to the boat's catch (i.e. multiply by a factor equal to the number of boxes that ship landed).
3. Add together the results for all sampled landings at that landing place in that month.
4. Raise to landings at given landing places for the month (i.e. multiply by a factor equal to the ratio of total landings by sampled landings).
5. Add together results for all landing places where samples were taken.
6. Raise to month's landings at all places (i.e. multiply by a factor equal to the ratio of total landings by landings at sampled places).
7. Add together results for all months to give landings for year.
Additional operations may be added to this sequence. Perhaps samples were only taken every other month; then the sum for the sampled months would be raised to give the year's landings, using the ratio of year's landings by landings in sampled months. At the other end of the sequence perhaps only part of a box is measured, and the initial operation might be to raise this sample to give the estimated contents of a complete box.
Samples of Tilapia caught by ring net on Lake Nyasa were measured during December 1945 and January 1946. Details are given in the following table (data adapted from Lowe, 1952).
|
Month |
Body length (cm) |
Total |
|||||||||||||||||||||
|
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
||
|
Dec. |
|
|
|
|
1 |
|
|
3 |
4 |
8 |
10 |
28 |
25 |
40 |
34 |
32 |
18 |
4 |
1 |
1 |
|
|
209 |
|
Dec. |
|
|
|
|
|
|
1 |
1 |
2 |
2 |
1 |
7 |
10 |
10 |
14 |
28 |
23 |
12 |
4 |
7 |
4 |
5 |
131 |
|
Dec. |
|
|
|
|
2 |
2 |
2 |
4 |
3 |
6 |
4 |
25 |
28 |
24 |
26 |
22 |
11 |
5 |
|
|
|
|
164 |
|
Jan. |
|
1 |
3 |
4 |
1 |
3 |
6 |
6 |
8 |
15 |
15 |
22 |
30 |
25 |
27 |
20 |
18 |
9 |
4 |
|
1 |
|
218 |
|
Jan. |
|
|
|
|
1 |
|
3 |
6 |
6 |
8 |
6 |
14 |
23 |
19 |
19 |
23 |
10 |
8 |
2 |
2 |
|
|
150 |
The first two samples were the complete catch of single hauls; the third and fifth samples were one half of the catch, and the fourth sample was one third of the catch of one haul.
1. Raise, where necessary, sample to give total catch of sampled haul.
2. Treating each month separately, raise sampled hauls to give total catch of each length for the month, and total for the two months, given that the catches in December and January were 118,000 and 120,000 fish respectively. [Note: raising factor for December = 118,000/(209 + 131 + 328).]
3. Calculate within-haul and between-haul variance of mean length for December.
The large between-haul variance in this example suggests that the best sampling system would be to take many small samples and that the sample size here (150-200 fish) might be too large. However, the sample technique used was to send observers on the fishing boats, and to measure the fish directly they were caught (which of course is the best system to avoid any sort of bias in fishermen sorting the fish for sale). This means that once the fish from one haul were measured no other group of fish was available to measure, i.e. essentially the time between samples was large. No advantage to the measuring program itself would be gained by reducing the size of sample, but of course there is always the possibility in this situation of the observers doing other work - measuring fish of other species, collecting data on maturity, feeding, etc.
Two raising factors were used in the example above; the second, going from the sum of the sampled catches to the whole month's catch, is based on normal statistics of catch which will presumably have been collected independently of the sampling program. The first factor, used to estimate the complete catch in the individual sampled hauls (used in the last three hauls), requires information which is only available at the time of sampling. Only if it is noted at the time whether the sample measured consists of all, a half or one third, etc. of the complete catch can the individual samples be combined with their proper weights to give the best estimate of the composition of the total catch. This is a general feature of nearly all sampling, that some information on quantities has to be collected at the time of measuring so that the correct raising factors can be calculated. The data required are the weight sampled and the weight of the catch from which the sample comes. Sometimes, when only part of a box of fish has been measured (because a complete box would be unnecessarily large), the fish remaining in the box which have not been measured will have to be counted to determine the proportion which has been measured. For instance a ship may land 18 boxes of whiting: 100 of the fish in one box are measured, and the rest from one box (125) counted. The raising factor is then
Where many samples are regularly taken, much work can be saved by suitable layout of the computations. If the measurements have been recorded say in centimeters, but ultimately the data is required in wider groupings, say 3-cm groups, then the work is reduced by making the grouping as early as possible, thus reducing the number of size groups for which computation is needed. Thus the data in Example 3.2.6.1 might well be grouped into 2-cm groups; and laid out as below.
|
Sample |
Length groups |
||||||||||||
|
12- |
14- |
16- |
18- |
20- |
22- |
24- |
26- |
28- |
30- |
32- |
Total |
Raising factor |
|
|
1 |
|
|
1 |
3 |
12 |
38 |
65 |
66 |
22 |
2 |
|
209 |
1 |
|
2 |
|
|
|
2 |
4 |
8 |
20 |
42 |
35 |
11 |
9 |
131 |
1 |
|
3 |
|
|
4 |
6 |
9 |
29 |
52 |
48 |
16 |
|
|
164 |
2 |
|
4 |
1 |
7 |
4 |
12 |
23 |
37 |
55 |
47 |
27 |
4 |
1 |
218 |
3 |
|
5 |
|
|
1 |
9 |
14 |
20 |
42 |
42 |
18 |
4 |
|
150 |
2 |
|
TOTAL |
3 |
21 |
23 |
71 |
131 |
255 |
438 |
429 |
206 |
33 |
12 |
1622 |
|
The appropriate raising factors have been noted at the end of each row, so that (if samples from both months are taken together) the estimated number of fish in each size group caught in the sampled hauls is given by the sums of products of two columns - a procedure which is easily carried out on most calculating machines.
Fishery biologists are concerned with a wide range of attributes of individual fish other than length - e.g. age, maturity, sex, meristic characters, etc. Direct sampling for these can of course be carried out in a similar way as length sampling. However, since the work involved for each fish is much greater and more time consuming than length measuring, it cannot easily be carried out on normal commercial landings, but requires that the fish should be brought back to the laboratory. There are exceptions: for instance, the sex of some species (e.g. plaice) can be determined very quickly - in suitable light conditions it can be seen as the fish are picked up to be placed on the measuring board. Thus, provided the recording form is suitably divided, separate length data on males and females can be obtained virtually as quickly as length data with no regard to sex. In some fisheries, e.g. redfish, plaice, characteristics of growth, etc. differ enough between males and females to make it desirable to treat them essentially as two different species, with length data, age composition, maturities, etc. all computed separately. Nearly the exact converse occurs in some tropical fisheries. Here several very closely related species may be caught at the same time. Measurements on the market can be referred only to the species group as a whole, and separation into species achieved only in detailed laboratory examination.
When sampling directly for age, etc., the same principles apply in choosing the sampling system as when sampling for length. Bias is avoided by sampling as soon after the fish are caught as possible, before any selection for various market conditions is made (or if this cannot be done, at least sampling from all market selections, and weighting the samples correctly). Variance is reduced by taking the right size of sample - which, because of the long time in taking the observations, and hence the large within-sampling time, is likely to be fairly small - and by choosing suitable stratifications.
In practice the need to avoid unconscious bias in selecting fish to include in the sample will require the actual size of sample to be considerably larger than that required to give the least variance. Thus the smallest unbiased sample is likely to be a complete box or basket (or half a box if the sampling is done carefully, taking all the fish from one side), or if the fish are not landed in containers, perhaps as many as 100 fish. This size is usually large, but not unreasonably large for efficient sampling with a quick operation such as measuring total length, but will involve quite appreciable inefficiency (in the sense of increased variance) with the longer operations such as age sampling. However, if direct age sampling is done, such inefficiency must be accepted, rather than introduce the risk of bias, which cannot be detected or corrected in subsequent analysis, and which could destroy the validity of most results.
Length sampling is essentially a very quick operation, and will normally be done at sea, or in a fish market during normal commercial operations, the fish once measured going back among the rest of the catch. Other observations, being long, and often involving mutilation of the fish, frequently require the fish to be bought by the research organization. Rather than buy the fish from the market, it may be possible to obtain the fish direct from the fisherman; ideally a sample would be put on one side during the actual fishing operation, with perhaps several such samples if the ship is, for example, a trawler fishing for several days on possibly three or four grounds. Such samples from a known position at a known time are potentially a great improvement on samples taken at the time of landing from fish possibly caught on several grounds. However, all will depend on the reliability of the fisherman, in putting the sample on one side at the time and place reported, and more particularly, on taking an unbiased sample of the catch. The difficulty in taking a relatively small unbiased sample from a catch on a fishing vessel's deck, even when there is no conscious selection, has already been mentioned (section 3.1). In addition there will always be the possibility, especially when fish are scarce and prices high, of the fisherman tending to put the poorer quality and less valuable fish into the scientist's sample.
Because, like many sources of bias, such selection is difficult to detect, it is often better to sample from the landings, where the entire sampling procedure can be controlled directly. An alternative would of course be to send a special observer to sea to collect the desired samples. The use of such special observers has already been discussed in connection with determining discards (section 3.1.4), and their time will be employed very inefficiently unless a wide range of information is being collected so that the actual time spent collecting any one item is small, but most of their available time is usefully occupied.
The normal procedure in sampling for age, maturity, etc. is therefore to bring a sample of moderate size - say 100 fish - from the fish market to the laboratory. Again, to avoid bias, it is better for fish to be bought by a scientist who actually goes down to the market, and best for the box actually taken to be selected by some random sampling procedure rather than sent up by a co-operative fisherman or merchant. Because of the rather high overhead costs of each sample in terms of value of the fish, time spent fetching them and finding out where they were caught, it is more efficient to make more than one type of observation. Thus the English herring sampling program, besides a large number of measurements on the market, consists of a number of laboratory samples. Each laboratory sample consists of 100 fish, each of which is weighed and measured, the scales are taken for age determination, maturity is determined and vertebrae are counted.
Many of the characteristics considered, for example, age, weight, maturity, etc., are closely related to the length of fish. Their distribution in the catches may therefore often be most easily estimated from a fairly large series of length measurements, together with a relatively small number of samples to give the relation between length and, say, age. In this way the total numbers in each length group in the catches (as estimated from the length measurements) are divided between the various ages in the same proportion as these ages appear in the key samples taken of that length group. Essentially each length group is treated separately.
(adapted from Fridriksson, 1934)
A sample of 100 cod between 50 and 100 cm were measured and their otoliths used to determine their ages. Fish under 9 years and over 11 years old were grouped together. The results are given in the following table.
|
Length (cm) |
Age (years) |
|||||
|
- 8 |
9 |
10 |
11 |
12 + |
Total |
|
|
50- |
3 |
1 |
|
|
|
4 |
|
60- |
3 |
10 |
|
|
|
13 |
|
70- |
7 |
32 |
1 |
7 |
|
47 |
|
80- |
1 |
8 |
3 |
6 |
|
18 |
|
90- |
|
3 |
3 |
5 |
2 |
13 |
|
100- |
|
|
|
1 |
1 |
2 |
|
TOTAL |
14 |
54 |
7 |
19 |
3 |
97 |
A separate series of length measurements gave estimates of the total numbers (in tens of thousands) of fish landed in each 10-cm group. These are given in the second column of the table below.
|
Length (cm) |
Total landed |
Estimated numbers landed of each age |
||||
|
- 8 |
9 |
10 |
11 |
12 + |
||
|
50- |
91 |
68 |
23 |
|
|
|
|
60- |
79 |
21 |
59 |
|
|
|
|
70- |
168 |
25 |
114 |
3 |
25 |
|
|
80- |
93 |
6 |
40 |
17 |
30 |
|
|
90- |
45 |
|
14 |
11 |
15 |
5 |
|
100- |
21 |
|
|
|
10 |
11 |
|
TOTAL |
497 |
120 |
250 |
31 |
80 |
16 |
The numbers of each age and size landed are estimated, and entered in this second table by dividing each number in the second column in the proportions of the age groups in the corresponding line of the first table. Thus in the age sample 25 percent of the 50-60-cm group were 9 years old. Therefore 25 percent of the total numbers of a 50-cm group =. 25 x 91 = 22.75 tens of thousands of fish are 9 years old. Similarly, the other entries are obtained (here rounded off) and by summing each column the estimates of the total numbers of each age are obtained. Computation is in fact easier by using a simple raising factor for each length group equal to the number landed: number in age sample, and multiplying each in the number of each age in the sample by this factor. Thus for the 50- group the raising factor (in tens of thousands) is 91/4 = 22.75, and the number of fish 8 years old and younger 3 x 22.75 = 68 (to nearest ten thousand).
If length data is being collected in any case, the advantages, in reduced chance of bias, and smaller variance, of this method of estimating age composition are very great. Assuming the length sampling is unbiased, then bias can only be introduced if, for fish of a particular size, fish of certain ages are more likely to appear in the age sample. This seems unlikely since selection, either unconsciously by the scientist picking up a few fish from a pile, or consciously by the fisherman sorting out fish for different types of buyer, is nearly always related to size. It seems difficult to imagine how any selection or bias could arise between 2 fish both say 35 cm, but one 3 years old and the other 5 years old. (Bias can arise if among the fish of a particular length group selected for sampling certain of them are rejected or not used because their scales or otoliths are too difficult for accurate age determination. These fish are likely to be the older ones of the length group and so there could be an underestimation of the abundance of old fish.) Much the same is true for other characteristics related to length, though possibly there might be sufficient difference in external appearance between immature and mature fish of the same length for bias to arise.
In Example 3.3.1 the number of fish in each length group whose age was determined was roughly proportional to the numbers landed in each length group. This is not necessary and indeed the numbers sampled in detail at each size can be chosen according to any desired system. In the landings the younger and smaller fish usually predominate, so that more of these young fish will occur in any random, or semi-random, sampling system. Their numbers are therefore likely to be estimated with relatively greater precision than those of the older fish. However, for many purposes, e.g. estimation of mortalities, it is desirable for the abundance of as many ages as possible to be estimated with fair and roughly equal precision; this can be achieved by increasing the sampling intensity on the bigger fish.
The variance in the estimates of the numbers in each age obtained by the use of such an age-length key such as that given in the tables above is given at once from the multinomial distribution. Thus if in a certain length group
N = number of fish in the landingsn = number of fish sampled for age
npi = number of fish in sample, age i
Ni = estimated number of fish, age; i, in the landings of the given size
then Ni = Npi
variance of npi = npi (1 -pi)
variance of Ni =
pi (1 -pi)
and coefficient of variation of
The estimated variance of the total numbers of a certain age landed of all sizes is given by simple addition (the variances in the different length groups can be added together because the sampling distributions in the various length groups are completely independent). The expression above for the variance assumes that N, the number of the given length group landed, is known precisely. In practice it too will have been estimated from some sampling procedure. An additional term should therefore be included, so that the proper estimate of the variance of Ni, is
Var
The first term is likely to be the larger, and in any case the presence of the additional term due to the variance of N does not reduce the desirability of making the first term as small as possible. It will be seen that the part of the variance due to estimation of pi is, as usual, inversely proportional to n, the number of fish sampled, so that the precision will be improved by any increase in sampling. However, it will also be improved if pi is large, and in fact as pi approaches unity, the variance falls toward zero, i.e. if nearly all the fish in the length group are the same age, then the numbers of fish of that age and size are known very precisely.
In using such an age-length key essentially three choices have to be made:
(a) how to divide the entire length composition between length groups;
(b) how, if at all, to divide the year - i.e. should a single key be used for the whole year, or separate keys for each month or quarter;
(c) how many fish to sample in each length group.
In choosing groupings by size of fish and season, which is another example of choice of strata of stratified sampling, it is as usual desirable that the strata should be so small that there is no marked difference in distribution (here in the proportion of the various ages) between possible subdividions of any single strata. There is also the desirability of decreasing the variance by making pi as large as possible, i.e. of making as far as possible each length group consist of a single age. This may well be possible at least for the smaller sizes where the fish grow fast and fairly uniformly. For instance the following table gives quarterly age-length keys for the smaller sizes of cod caught in the North Sea in 1960, in terms of the numbers of fish of each age in the samples.
|
Length group |
30-39 |
40-49 |
50-59 |
60-69 |
70-79 |
|||||||||||||||
|
Quarter |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
|
1 year old |
|
|
12 |
56 |
|
|
1 |
23 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 years old |
36 |
26 |
36 |
8 |
62 |
51 |
73 |
50 |
15 |
41 |
54 |
63 |
|
2 |
13 |
43 |
|
|
|
|
|
3 years old |
1 |
4 |
|
|
4 |
1 |
3 |
2 |
18 |
9 |
6 |
2 |
19 |
21 |
25 |
17 |
4 |
28 |
27 |
30 |
|
4 years old |
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
3 |
|
11 |
20 |
7 |
7 |
6 |
|
5 years old |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
9 |
|
|
|
|
TOTAL |
37 |
30 |
48 |
64 |
66 |
52 |
77 |
75 |
35 |
50 |
61 |
65 |
21 |
27 |
38 |
71 |
33 |
35 |
34 |
36 |
So far as choice of seasonal groupings is concerned, the two smaller sizes in particular show very big changes during the year, so that a single grouping for the year is unsuitable. However, there is not much difference between successive quarters (except for the smallest size), so that there is probably even less difference between months. Quarters, therefore, are at least a fine enough subdivision of the year, and even two half-yearly age-length keys would be reasonably satisfactory. For the big fish, 70-79 cm, and still more for the bigger fish for which data are not given in the table, there is little seasonal change. For these, therefore, a single annual age-length key would be suitable. There is no basic reason why different periods for different length groups should not be used in this way. However, in practice it may be more convenient to use the same time intervals for all length groups - here, then, two half-yearly age-length keys seem best.
There are no very abrupt changes between length groups. Thus the proportions of the three year old fish in the first quarter, for each of the five length groups, are 0.03, i.e. 1/37, 0.06, 0.51, 0.90 and 0.12 respectively. This suggests that there would be no very big differences between the age distribution of fish say in the 5-cm groups 40-44 and 45-49, and this is in fact confirmed by analysis of the original data. Thus 10-cm length groups are sufficiently small. However, there are sufficient differences between 10-cm groups to show that any coarser grouping, e.g. in 15-cm or 20-cm groups, would not give such precise estimates.
The optimum numbers sampled in each length group are likely to depart quite widely from the proportions likely to be obtained by random sampling from the landings as a whole. In the landings the majority of the fish are likely to be concentrated in the smaller length groups.
The number of fish of the ages represented in these groups will therefore be known very precisely, while the estimates of the numbers of older fish will have considerable variance. For many purposes it is probably desirable to have the numbers of at least the more important ages estimated with roughly equal precision. For instance, if the mortality is being estimated as the ratio of five year old to four year old fish, it is little help if the number of four year old is known very precisely if at the same time the number of five year old fish is only badly estimated. A reasonable system of sampling would therefore be to take equal numbers for age analysis from each length group. In fact, even then the younger ages may be estimated more precisely, as at least for fast and uniformly growing fish each of the smaller length groups may be comprised of almost entirely one age group, thus reducing the term (1 -pi) in the expression for the variance, var N = N2  pi (1-pi). In contrast the larger sizes will contain fish of several different ages.
pi (1-pi). In contrast the larger sizes will contain fish of several different ages.
Using the age-length data for cod given in the previous table, and the fact that the estimated number of fish in thousands landed each quarter was as follows:
|
Quarter |
1 |
2 |
3 |
4 |
|
30-39 |
202 |
275 |
160 |
270 |
|
40-49 |
327 |
675 |
488 |
508 |
|
50-59 |
107 |
200 |
394 |
673 |
|
60-69 |
109 |
116 |
205 |
329 |
|
70-79 |
43 |
70 |
139 |
104 |
estimate the number of fish of each age, 1 to 5, less than 80 cm, landed each quarter, and the total for the year. Also estimate the total for the year from a single age-length key for the year.
Assuming the numbers landed of each size are known precisely, calculate the variances of the estimates of the numbers of each age, using quarterly and annual age-length keys.
Data from several sources
Apart from their use for improving the efficiency of sampling in a single simple fishery, age-length keys (or maturity-length keys, etc.) are invaluable in any mixed fishery, where the same stock is being exploited with a number of different gear, or different countries. However similar two groups of vessels may appear to be, it is very unlikely that even when fishing the same stock their catches or landings will have precisely the same composition, in terms of length, age, etc. Differences may arise through the more obvious types of selection, e.g. escape of the smaller fish through the meshes of a trawl, or other types of gear selection - or, and possibly most often, through differences in the precise grounds fished. Whatever the causes, the result is that samples taken from catches of one type of gear, or by ships from one port, or one country, cannot be taken as representing satisfactorily the landings by other gear, or in other ports or countries. The differences between the landings are essentially in the sizes of fish, and the relation between, say, age and length is the same for all - that is, just as any selection by a scientist sampling the fish after landing is related to length, and not to the age of the fish of a given length, so will the gear select by size of fish, and will not in general be able to discriminate between, say, 2- and 3-year old fish of 30 cm. There are, of course, exceptions; gear selection in the strict sense is unrelated to age, for a given length, but two ships can fish grounds with different size composition of fish, and with different growth rates.
It should be noted that if two grounds have noticeably different growth rates, then the mixing between them cannot be very rapid, and they may have to be treated separately, not only in the sampling, but also in subsequent analysis.
In general though it can be taken as a rule that samples of length composition should be taken from all groups of vessels exploiting a stock of fish (from each gear, each country, etc.), age-length keys can be derived from only a section of the fishery, and then be applied to the length compositions of all landings.
During 1960 seiners landed at Grimsby from the North Sea the following numbers of cod (in thousands) under 80 cm:
|
Quarter |
1 |
2 |
3 |
4 |
|
30-39 |
2 |
2 |
5 |
18 |
|
40-49 |
12 |
55 |
138 |
87 |
|
50-59 |
6 |
66 |
196 |
70 |
|
60-69 |
5 |
43 |
80 |
14 |
|
70-79 |
3 |
42 |
91 |
6 |
Using the age-length keys derived from the trawler landings, estimate the numbers of fish at each age.
Ideally, of course, age data, or samples for constructing an age-length key, should be taken from all, or as many sections of the fishery as possible. Even then it is best to combine all age-length data together to give a single age-length key, which can then be applied either to the total landings of each length group, to give the total age composition, or to each section (e.g. landings by a particular gear) separately to give the separate age composition. This of course is essentially a problem in stratified sampling; each length group can be considered as an independent population, for which the number at each age has to be estimated. Stratification, i.e. treating each section of the landings separately, will not be an advantage because the distributions of age (for a given length) within each section are the same, and will give increased variance unless sampling is done precisely in proportion to the numbers in each section, and such an exact apportioning of sampling effort is unlikely to be achieved in practice.
Such pooling of data of age length is likely to be particularly valuable in an international fishery. Age determination, or similar work, is not only time consuming but also requires a fair degree of skill and experience. Not all countries exploiting a stock of fish may be able to collect age data - e.g. due to shortage of suitable staff, but all should be able to sample for length composition. Age data for the entire landings may then be obtained, either by the appropriate international agency using length data from all sources, and all available age-length data, or nationally, provided that where age data are available they are published in the form of age-length keys.