3. CROISSANCE

3.1 Croissance exprimée en longueur ou en poids
3.2 Conversion de la longueur en âge
3.3 Exercices

3.1 Croissance exprimée en longueur ou en poids

En matière d'analyse des populations, il est bon de pouvoir exprimer par une formule mathématique la croissance des animaux aquatiques. Il faut essentiellement une formule raisonnablement facile à incorporer dans les équations de rendement, conforme aux données d'observation sur la taille à divers âges, et donnant la taille (exprimée en longueur ou en poids) à tel ou tel âge. En fait, l'analyse d'une population s'attache davantage au taux de croissance - à l'augmentation de poids ou de longueur par unité de temps - qu'à la taille à divers âges, car maints problèmes d'évaluation halieutique reviennent essentiellement à comparer le gain de poids dû à la croissance à la diminution causée par la mortalité naturelle. Parfois, notamment lorsqu'on étudie l'incidence d'une augmentation de la taille à la première capture, il est particulièrement important de connaître la vitesse de croissance pour une tranche de vie relativement brève: celle que met l'animal pour passer de l'ancienne à la nouvelle «taille à la première capture». Aussi y a-t-il de bonnes raisons pour préférer, toutes autres choses égales d'ailleurs, une méthode permettant d'ajuster les équations aux données sur le taux de croissance, plutôt qu'aux correspondances taille/âge.

Il est souhaitable que la formule de croissance possède d'autres qualités: être facile à ajuster aux données observées, comporter peu de constantes (qui devront autant que possible avoir une signification biologique), et ne pas donner des résultats illogiques en cas d'extrapolation aux âges situés en dehors des limites des données utilisées.

Il existe maints ouvrages - et leur nombre augmente constamment - sur les équations de croissance, mais aucune de celles-ci, malgré leur variété, ne donne entièrement satisfaction pour toutes les situations. En vérité, il serait bien surprenant qu'une formule simple puisse toujours décrire la croissance même d'un seul animal aquatique durant la majeure partie de sa vie, si l'on songe aux différences considérables pouvant exister en matière de disponibilité alimentaire, d'épuisement consécutif au frai, etc. Sans essayer de passer en revue toutes les équations de croissance, on s'est attaché principalement ici à une formule particulière, celle qui est créditée à von Bertalanffy (1938), et qui répond aux deux principaux critères: elle s'adapte à la plupart des données de croissance observées, et peut être facilement incorporée dans les modèles d'évaluation des stocks.

Si l'on porte sur un graphique la longueur d'un poisson, crustacé ou bivalve en fonction de son âge, on obtient une courbe dont la pente décroît continûment quand l'âge augmente, et qui s'approche d'une asymptote supérieure parallèle à l'axe des X (figure 3.1.1). Les courbes du poids en fonction de l'âge s'approchent elles aussi d'une asymptote supérieure, mais sont habituellement sigmoïdes asymétriques, l'inflexion se faisant au tiers environ du poids asymptotique (figure 3.1.2).

FIGURE 3.1.1. - Courbe de croissance en longueur.

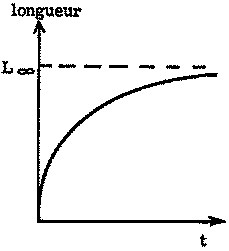
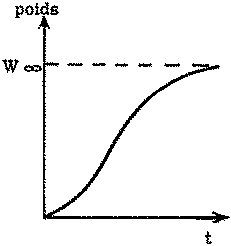
FIGURE 3.1.2. - Courbe de croissance en poids.

Si l'on inscrit la vitesse de croissance en longueur en fonction de la longueur, on obtient fréquemment une droite coupant l'axe des X en un point L_¥ au-delà duquel le poisson ne grandit plus, et qui correspond à l'asymptote de la courbe longueur/âge. Si l'on a une relation linéaire entre taux de croissance en longueur et longueur, cela signifie, en termes mathématiques:

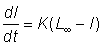, (3.1)

où L_¥ est la valeur de l correspondant à un taux d'accroissement égal à 0. Nous avons là une fonction linéaire: y = ax + b, dans laquelle a = - K et b = KL_¥ . Pour intégrer cette équation différentielle, nous l'écrivons sous la forme:

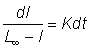(voir section 2)

et par conséquent: - log (L_¥ -l) = Kt + constante

ou: L_¥ - l = e^-Kt × constante

ou encore: l = L_¥ - constante × e^-Kt

Si t₀ est l'âge théorique auquel l = 0, la valeur de la constante sera donnée par l'équation:

0 = L_¥ - constante × ou constante =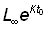

et alors:

, (3.2)

L'équation 3.1 est identique à celle qu'a obtenue von Bertalanffy sur des bases physiologiques en considérant la croissance pondérale comme le résultat de deux processus opposés: anabolisme et catabolisme, celui-là étant proportionnel à la surface (s) des organismes et celui-ci à leur poids (w).

En d'autres termes:

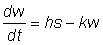
ce qui, w étant proportionnel au cube de la longueur des organismes et s au carré de leur longueur, donne, si l'on divise chaque membre de l'équation par le carré de la longueur:

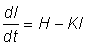
Quand on construit la courbe de croissance point par point, ce qui apparaît n'est pas le taux instantané de croissance, mais seulement des longueurs à des temps donnés - souvent chaque année si les données proviennent de travaux de détermination de l'âge, mais à intervalles irréguliers si l'on a utilisé les résultats de marquages. Si les temps t₁ et t₂ sont rapprochés, une bonne approximation du taux instantané de croissance est donnée par 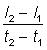, où l₁ et l₂ sont les longueurs aux temps t₁ et t₂. Si l'on porte sur un graphique cette vitesse de croissance en fonction de la longueur moyenne 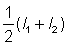. on obtient un point de la courbe de l'équation 3.1. L'intersection de cette courbe avec l'axe des x donne une estimation de L_¥ , et sa pente une estimation de - K.

Si nous connaissons les longueurs à des intervalles de temps égaux T, nous avons, en reprenant l'équation 3.2:

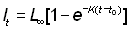
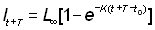
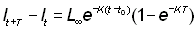
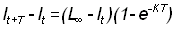, (3.3)

La courbe de l'accroissement (l_t+T - l_t) en fonction de la longueur initiale (l_t) est une droite de pente - (1 - e^-KT) et dont l'intersection avec l'axe des X est L_¥ (figure 3.2.1). Lorsque T = 1 an, on obtient une courbe particulièrement intéressante de pente - (1 - e^-K).

L'équation 3.3 peut aussi s'écrire:

l_t+T = L_¥ (1 - e^-KT) + l_t e^-KT, (3.4)

qui, quand T = 1, est l'expression de la courbe bien connue de Ford-Walford, de l_t+1 en fonction de l_t, droite de pente de e^-K et qui coupe la bissectrice des axes de coordonnées (quand l_t = l_t+1) au point d'abscisse L_¥ (figure 3.2.2). Cette courbe est essentiellement la même que la courbe de l'accroissement (l_t+1 - l_t) en fonction de la longueur initiale. Les points semblent mieux s'adapter à la courbe de Ford-Walford, mais, comme l'intersection de la droite de régression et de la bissectrice se fait très obliquement, L_¥ est en fait déterminé par les deux courbes avec une précision égale; si la courbe est construite graphiquement, plutôt que par calcul des lignes de régression (méthode des moindres carrés par exemple), on risque de plus grandes erreurs avec la courbe l_t+1 en fonction de l_t (courbe de Ford-Walford).

FIGURE 3.2.1. - Estimation des constantes de croissance. Représentation de l'accroissement de longueur par rapport à la longueur initiale.

FIGURE 3.2.2. - Estimation des constantes de croissance. Représentation de la longueur par rapport à la longueur un an auparavant (courbe de Ford-Walford).

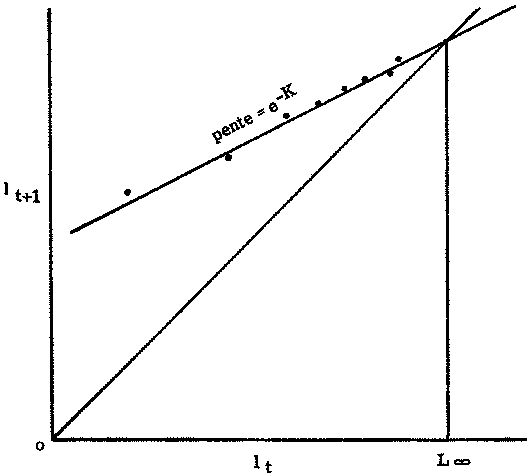
L_¥ et K peuvent être déterminés directement à partir des courbes de ces graphiques, soit par analyse de régression soit à main levée; t₀ peut alors être estimé à partir de l'équation 3.2 pour n'importe quelle combinaison de données de longueur et d'âge. A cette fin, l'équation 3.2 peut s'écrire comme suit:

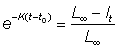
ou

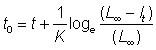, (3.5)

Toutefois, si l'on peut obtenir ainsi une estimation de t₀ pour tout âge quand on connaît la longueur moyenne correspondante, toutes ces estimations ne seront pas également valables. Pour un poisson âgé, elles pourront varier considérablement, car lorsque l_t est presque égal à L_¥ une petite différence dans l_t en introduit une grande dans l'estimation de t₀. Pour les jeunes, au contraire, un biais peut apparaître dans l'évaluation de la longueur moyenne, seuls les plus gros d'entre eux étant capturés. Ainsi, la meilleure estimation de t₀ devrait être la moyenne des estimations de t₀ obtenues pour les groupes d'âge jeunes, mais pleinement représentés.

D'autre part, seul L_¥ est estimé à partir des courbes représentatives de l'accroissement par rapport à la longueur initiale. On peut calculer 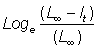, ce qui fournit un moyen graphique pour rechercher t₀. A partir de l'équation 3.5, on calcule la droite de pente - K qui coupe l'axe des X en t₀.

Il existe diverses façons d'obtenir et de ranger en tableaux des longueurs à intervalles annuels. La plus simple est probablement l'analyse de la croissance d'un seul poisson, sa longueur à la fin de chaque année étant déterminée par mesures effectuées sur écailles, otolites, etc. Il est également possible de «suivre» l'ensemble des animaux d'une même classe d'âge durant un certain nombre d'années - par exemple pour la classe d'âge 1956, la croissance pendant la cinquième année de vie est représentée par la différence de longueur moyenne entre la fin de 1961 et la fin de 1960. Les deux méthodes s'attachent à la croissance d'un groupe de poissons, chaque année de vie correspondant à un point de la courbe. Ainsi, les intervalles de croissance se rapportent à différentes années civiles: pour la classe 1956, l'accroissement durant la troisième année est attribué à 1959, peut-être dans des conditions différant beaucoup de celles de 1961, cinquième année de vie. On peut étudier la croissance durant une année particulière en s'attachant à la croissance de différentes classes d'âge au cours de la même année - par exemple, en 1960, l'accroissement au cours de la quatrième année entre les classes d'âge 1957 et 1956, etc. En réalité, ces différences ne correspondent pas à la croissance véritable d'un poisson ou groupe de poissons particulier, et cette méthode ne doit être employée que lorsque les autres ne sont pas applicables. On peut l'améliorer en prenant pour chaque âge la moyenne de la taille sur un certain nombre d'années, mais il est alors généralement possible, et plus satisfaisant, d'analyser la croissance de chacune des classes d'âge ou durant chaque année civile.

Le poids d'un poisson étant en général étroitement proportionnel au cube de sa longueur, on peut écrire, à partir de l'équation 3.2:

, (3.6)

où W_¥ est le poids asymptotique correspondant à la longueur asymptotique L_¥ .

De même, si le poids est proportionnel à la n^ième puissance de la longueur:

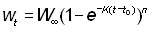
Quand les données sont exprimées en poids, l'établissement des courbes de croissance est extrêmement facile si l'on utilise la racine cubique du poids comme indice de longueur, en résolvant alors comme ci-dessus les équations de croissance, et en portant au cube les résultats finals pour les exprimer en poids.

Richards a donné (1959) une équation de croissance plus générale. C'est, avec un léger changement dans la notation:

, (3.7)

Pour diverses valeurs de m, cette équation devient l'une ou l'autre des équations de croissance courantes. Ainsi, pour 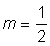, l'équation 3.7 devient l'équation (3.2) de von Bertalanffy. Pour m = 2 nous avons, avec quelques modifications, l'équation autocatalytique:

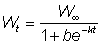
et, pour m = 0, l'équation monomoléculaire:

w_t = W_¥ (1 - ae^-kt)

On démontre en outre que, quand m tend vers 1, l'équation devient l'équation de Gompertz, log w_t = log W_¥ (1 - ae^-Kt). La courbe correspondante représente un rapport identique à celui de l'équation 3.1, avec la différence que les longueurs sont exprimées en logarithmes.

3.2 Conversion de la longueur en âge

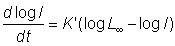
Les expressions ci-dessus donnent le poids ou la longueur d'un poisson en fonction de son âge. Il faut parfois avoir recours au processus inverse, pour connaître l'âge d'un poisson de telle ou telle longueur: les données sur la sélectivité des engins, par exemple, normalement exprimées par des longueurs, doivent être converties en âges pour pouvoir être incorporées dans les équations de rendement.

Si le schéma saisonnier de croissance est très accusé et si tous les poissons d'un certain âge sont à peu près de la même longueur, il se peut que l'âge moyen effectif du poisson d'une certaine longueur diffère beaucoup de l'âge moyen obtenu à partir de la courbe de croissance annuelle moyenne, particulièrement au début et à la fin de l'époque de croissance rapide. Dans ce cas, il vaut mieux procéder empiriquement et convertir les longueurs en âges à partir de la courbe observée âge/longueur. De plus, notamment si la croissance varie beaucoup d'un individu à l'autre, la courbe de la longueur moyenne à un âge donné différera de la courbe de l'âge moyen à une longueur donnée (de même qu'en général la droite d'ajustement de y en fonction de x diffère de la droite d'ajustement de x en fonction de y). Il suffit toutefois généralement de convertir la longueur en âge à partir d'une équation de croissance fondée sur toutes les données observées de longueur moyenne à certains âges, autrement dit l'équation de von Bertalanffy:

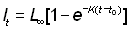
Pour obtenir t en fonction de l, divisons les deux termes de l'égalité par L_¥ et soustrayons de l'unité:

Exprimée en logarithmes naturels, l'équation devient:

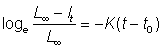
et par conséquent

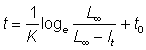, (3.8)

La différence d'âge t₂ - t₁ entre deux longueurs l₂ et l₁ est donc:

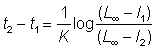, (3.9)

3.3 Exercices

1. L'équation de croissance de von Bertalanffy contient trois paramètres (L_¥ , K et t₀), qui peuvent être obtenus à partir de trois observations de longueur à un certain âge. A partir de l'équation 3.2, exprimer les longueurs aux temps t - 1, t, t + 1 et les accroissements de longueur entre t - 1 et t et entre t et t + 1. Déterminer ensuite une valeur estimée de K à partir du rapport entre ces accroissements. En remplaçant, dans l'équation 3.2, K par cette estimation, ou d'une autre manière, trouver une valeur pour L_¥ en fonction de l_t et des accroissements.

2. Kitahama (1955) donne, pour le hareng du Pacifique Clupea pallasii C. et V. capturé au large de la côte ouest de Hokkaido de 1910 à 1954, les données suivantes (taille en fonction de l'âge). Les longueurs sont des moyennes établies sur 45 ans: l'âge a été déterminé par examen des anneaux des écailles.

Age	Longueur totale
(années)	(cm)
3	25,70
4	28,40
5	30,15
6	31,65
7	32,85
8	33,65
9	34,44
10	34,97
11	35,56
12	36,03
13	35.93
14	37,04
15	37,70

W=7,8 × 10^-3 L³ g

a) Construire une table de travail et déterminer L_¥ , W_¥ , K et t₀.

b) Calculer les courbes théoriques de croissance en longueur et en poids pour la période 0-15 ans.

3. Yokota (1951) fournit les données suivantes pour la croissance du requin Mustelus kanekonis (âge déterminé sur la base des modifications saisonnières de la longueur des myxoptérygies).

	Age	Poids
	groupes	g
I		375
II		1 519
III		2430
IV		3 247

W = 7,4 × 10^-3 L³ g

a) Déterminer L_¥, W_¥ , K et une valeur calculée pour t₀.

b) Calculer les courbes de croissance en longueur et en poids jusqu'au groupe d'âge VIII.

4. Après un marquage de pétoncles géants, Posgay (1953) a recueilli les données suivantes concernant la croissance durant les dix mois environ s'étant écoulés jusqu'à la recapture.

	Diamètre de la coquille
	mm
Au marquage	64	69	71	94	104	105	110	117	117	126
A la recapture	98	102	93	115	120	126	125	127	136	138

a) Calculer L_¥ et K.

b) En prenant t₀ = 0, calculer et tracer la courbe de la croissance en longueur jusqu'à l'âge de six ans.

5. Ochiai (1956) fournit les données suivantes sur la croissance des soles Heteromycteris japonicus et Pardachirus pavoninus:.

Age	Longueur standard
	H. japonicus	P. pavoninus
	cm
1	6,09	10,00
2	8,10	14,80
3	9,20

a) Déterminer arithmétiquement L_¥ , K et t₀ pour chaque espèce (en supposant t₀ = 0 pour P. pavoninus)

b) Tracer les courbes de croissance pondérale, en supposant un rapport cubique entre poids et longueur.

6. Moiseev (1946) a publié les données suivantes concernant la croissance (longueur totale en cm) de la limande Limanda aspera du golfe de Pierre-le-Grand (mer du Japon).

Age	Sexe	ANNÉE D'ÉCHANTILLONNAGE
		1928	1930	1931	1932	1933
1		5,15	7,60	6,58	7,72	8,34
		5,77	7,22	7,20	9,50	7,34
2		10,25	13,60	11,70	13,80	14,10
		11,77	11,88	13,20	15,50	12,68
3		16,40	19,40	17,42	18,82	19,44
		17,41	19,00	18,80	21,00	18,68
4		20,45	24,00	21,22	22,92	24,32
		22,13	25,00	23,60	25,50	25,32
5		25,05	26,80	25,42	26,38	27,66
		26,51	26,12	27,60	29,50	27,32
Indice de la prise démersale totale		1	1	5,5	8,0	7,7

a) Analyser les différences sexuelles du point de vue de la croissance.

b) Tenant compte du fait que la pêche n'a été menée en grand dans le golfe que lors de la campagne 1929-30 et que L. aspera constituait 80 pour cent de la prise démersale, étudier les variations de croissance d'une année à l'autre. La composition moyenne par âge, en fonction du nombre, de 1931 à 1933, était:

Age	3	4	5	6	7	8	9	10	11	12
Pour cent	0,6	4,7	16,1	33,3	27,9	11,3	3,4	1,7	0,9	0,2

c) Estimer le coefficient de mortalité totale et examiner les données relatives à la croissance pour voir si la longueur moyenne à un âge donné est affectée d'un biais dû à la sélection.

(Cette partie de l'exercice n'est à faire qu'après l'étude des chapitres 5 et 7.)