9.1 Dérivation de l'équation du rendement
9.2 Autres expressions de l'équation du rendement
9.3 Exercices
On s'est attaché jusqu'ici aux méthodes de collecte des données fondamentales et à leur analyse en vue d'obtenir des valeurs estimées des paramètres de base intéressant les populations: croissance, mortalité, âge au recrutement, etc. Dans le présent chapitre et les suivants, on traite de la manière d'utiliser ces estimations pour expliquer et comprendre le passé d'une pêcherie et prédire son avenir, et plus particulièrement pour prévoir l'incidence de modifications de la pêche découlant de mesures envisagées en matière de protection ou de régulation.
Le cas le plus simple est celui d'un stock pour lequel les paramètres sont constants. Le mieux est alors de calculer la production d'une seule classe d'âge durant toute sa vie, qui sera, dans l'hypothèse d'une situation stable, identique à la production annuelle de toutes les classes d'âge présentes dans la pêcherie. On peut diviser toute la vie d'une population en périodes relativement courtes et, pour chacune d'elles, déterminer le nombre d'animaux vivants, le nombre péché, les morts par mortalité naturelle (non causée par la pêche), et les survivants au début de la période suivante, ainsi que la production pondérale (produit du nombre d'animaux péchés par leur poids moyen). Cela peut se faire arithmétiquement, mais comme pour opérer avec précision les périodes choisies doivent être brèves, et par conséquent nombreuses, les calculs seront fastidieux. Il est beaucoup plus facile d'exprimer le rendement par une formule algébrique, qui présente le grand avantage de montrer explicitement l'influence des divers paramètres sur la production.
Nous emploierons les symboles suivants:
Nt = nombre de poissons vivants au temps t
R = nombre de recrues, autrement dit nombre de poissons vivants à l'âge tr
R' = nombre de poissons vivants à l'âge tc, où ils sont pour la première fois capturés par l'engin de pêche
M = coefficient instantané de mortalité naturelle
F = coefficient instantané de mortalité par pêche
On a alors, pour tr < t < tc:
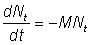
autrement dit, le taux instantané de mortalité naturelle des animaux est égal au produit du coefficient de mortalité naturelle par le nombre d'animaux.
D'où

et
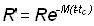
Pour t > tc, lorsque interviennent mortalité par pêche et mortalité naturelle:
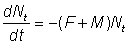
et
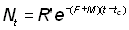 , (9.1)
, (9.1)
ou encore

Le nombre d'animaux péchés entre les temps t et t + dt sera F. Ntdt, de sorte que l'on obtiendra le nombre total de captures, C, en divisant le temps total écoulé entre tc (âge à la première capture) et tL (âge maximal atteint) en brefs intervalles, et en additionnant le nombre péché dans chacun d'eux.
Mathématiquement, nous l'exprimons par l'intégrale (voir chapitre 2):
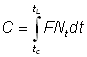
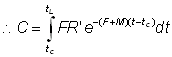
et, en intégrant:
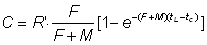 , (9.2)
, (9.2)
et, si tL est suffisamment grand pour que l'on puisse négliger 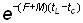 on a:
on a:
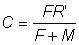 , (9.2')
, (9.2')
Ainsi, le nombre d'animaux péchés est une fraction du nombre total atteignant l'âge à la première capture, égale au rapport entre le coefficient de mortalité par pêche et le coefficient de mortalité totale.
De même, le poids capturé entre les temps t et t + dt est donné par la formule:
dYt = FNtWtdt
où Wt est le poids moyen d'un animal d'âge t.
Le poids total capturé sera donc donné par la formule:
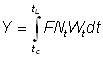 , (9.3)
, (9.3)
Pour intégrer aisément cette formule, il faut donner à l'expression du poids une forme appropriée. Parmi les équations de croissance examinées plus haut, l'une des plus pratiques est celle de von Bertalanffy. Nous pouvons écrire:
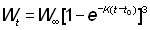
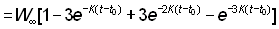
Ou bien, en présentant l'expression entre parenthèses sous forme de sommation:
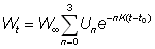
où
U0 = 1, U1 = -3, U2 = 3, U3 = -1
On a alors:
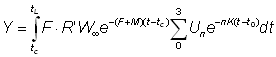
ou bien, en écrivant t - t0= (t - tc) - (tc - t0) et en réarrangeant les termes:
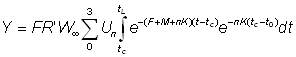
ce qui devient, en intégrant:
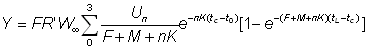 , (9.4)
, (9.4)
Cette expression peut être simplifiée si l'on prend tL suffisamment grand pour pouvoir négliger le dernier terme. On peut alors exprimer le rendement par la formule:
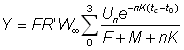
ou bien, en remplaçant R' par sa valeur:
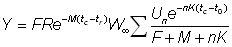 , (9.5)
, (9.5)
D'autres quantités sont importantes en dehors de la production totale. Par exemple, le rendement représente F fois la biomasse moyenne des animaux se trouvant dans la phase exploitée B'. On a donc:
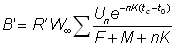 , (9.6)
, (9.6)
De même, de l'équation 9,2', on peut tirer une estimation du nombre moyen d'animaux dans la phase exploitée en divisant la prise en nombre par F:
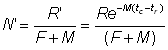
Le poids moyen de chaque animal dans la phase exploitée est donc:
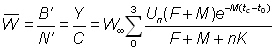
Le recrutement étant inconnu et souvent variable, les rendements, etc., sont habituellement exprimés en rendement, etc., par recrue.
Les tables de travail qui figurent ci-après indiquent la marche à suivre pour calculer le rendement directement à partir de l'équation 9.5. La table A permet la recherche du rendement pour différentes valeurs de la mortalité par pêche F, la sélectivité tc étant constante. Nous porterons dans la case située en haut et à gauche les valeurs des divers paramètres du stock, en utilisant, soit les meilleures estimations disponibles, soit, si les connaissances ne sont pas suffisamment précises, une gamme de valeurs de la mortalité naturelle, etc. On emploiera un feuillet séparé pour chaque série de valeurs possibles. Au milieu, en haut, sont indiquées diverses opérations, les mêmes pour toutes les valeurs de F. Au-dessous, les quatre paires de colonnes (B) et (C) correspondent aux quatre termes de la sommation de l'équation 9.5. (Pour plus de facilité, la plupart des rubriques, colonnes, etc., sont désignées par des lettres, qui sont mises entre parenthèses lorsqu'elles sont reprises dans les entêtes suivants, pour éviter une confusion avec les termes des équations. A la seconde ligne pleine de l'en-tête figure, pour chaque colonne, la formule qui sera normalement utilisée pour calculer l'indication à y porter. A la troisième ligne est indiquée la signification de cette indication en fonction des divers paramètres.)
Les tables de travail B.1 et B.2 servent à calculer le rendement pour diverses sélectivités d'engins de pêche. La première est utilisée pour le calcul de tc et des valeurs connexes à partir de la sélectivité, normalement définie par la taille à la première capture lc. On peut alors calculer le rendement pour toutes les sélectivités et pour n'importe quelle valeur de la mortalité par pêche, comme dans la table B.2, qui est pratiquement identique à la table A.
Il est possible de simplifier les calculs, tout en faisant entrer en ligne de compte un autre rapport longueur/poids que le rapport cubique, en exprimant le rendement Y sous une autre forme par une fonction bêta incomplète.
Cette fonction, généralement exprimée Bx, (p, q), est définie par l'intégrale
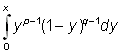
où p et q sont des constantes positives, la limite supérieure d'intégration x se situant entre 0 et 1. Pour x = 1, l'expression constitue la fonction bêta complète: B (p,q).
Pour exprimer le rendement au moyen de la fonction bêta, nous pouvons écrire, à partir de l'équation 9.3 et pour tL = ¥:
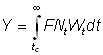
où
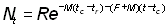
ce qui, si l'on remarque que t - tc = (t - t0) - (tc - t0), peut être exprimé de la manière suivante:
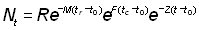
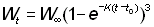
ou bien, si W¥ est proportionnel à lb:
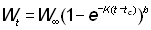
En opérant la transformation:
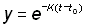
et en calculant les limites d'intégration pour la nouvelle variable,
t = ¥ devient y =0
et
t = tc devient 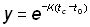
De plus, l'expression 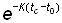 , qui est égale à
, qui est égale à 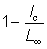 , sera représentée par 1 - c.
, sera représentée par 1 - c.
Les différents facteurs de l'intégrale deviennent alors:
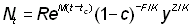
Wt = W¥ (1-y)b
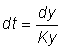
Le rendement pondéral. Y, devient alors:
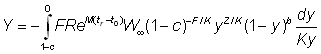
ou, en écrivant 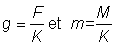 :
:
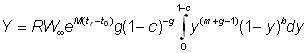
Si l'on représente l'intégrale par une fonction bêta incomplète, on a:
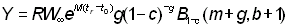
ou, si b = 3:
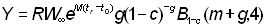 , (9.7)
, (9.7)
L'expression ci-dessus du rendement peut être subdivisée en deux éléments: le premier (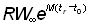 ) ne contient aucun des deux paramètres (F ou tc) déterminés par l'intensité ou le mode de pêche. Cet élément peut donc être considéré comme une constante lorsqu'on étudie l'incidence de différents modes de pêche sur le rendement. Le second élément renferme seulement quatre paramètres: le rapport m = M/K et g=F/K, b, et c.
) ne contient aucun des deux paramètres (F ou tc) déterminés par l'intensité ou le mode de pêche. Cet élément peut donc être considéré comme une constante lorsqu'on étudie l'incidence de différents modes de pêche sur le rendement. Le second élément renferme seulement quatre paramètres: le rapport m = M/K et g=F/K, b, et c.
Il existe des tables de la fonction bêta incomplète (Jones, 1957; Wilimovsky et Wicklund, 1963). Holt (1957) a élaboré des tables de g (1 -c)g. On peut donc exprimer le rendement comme le produit d'une constante et de deux valeurs données par les tables.
On remarquera que:
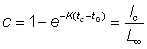
et constitue donc la proportion de la croissance totale en longueur qui a lieu avant que l'animal n'entre dans la phase exploitée. L'expression du rendement, en dépit de sa complexité apparente, n'est déterminée que par quelques valeurs: la proportion de la croissance achevée lorsque l'animal est recruté, et les ordres de grandeur relatifs de la mortalité par pêche, de la mortalité naturelle, et du paramètre de croissance K.
Etant donné que dans là pratique b s'écarte rarement beaucoup de 3, on peut généralement employer l'équation 9.7. Si l'on excepte la constante du début, cette équation ne comporte que trois variables indépendantes C, g et m, et il est facile de poser directement une fonction comprenant trois variables. Beverton et Holt 1964 l'ont fait explicitement comme fonction de 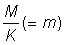 , c et
, c et 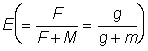 . Ils ont obtenu une formule légèrement différente, mais il est aisé, du point de vue mathématique, d'exprimer leur expression (12)
. Ils ont obtenu une formule légèrement différente, mais il est aisé, du point de vue mathématique, d'exprimer leur expression (12) 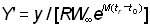 en fonction de c, m et g:
en fonction de c, m et g:
dont on peut montrer qu'il est égal à: g (1 -c)-g B1-c (m + g, 4).
Ces tables de rendement ont été établies pour une série de valeurs de 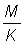 allant de 0,25 à 5,00. Pour chaque valeur de
allant de 0,25 à 5,00. Pour chaque valeur de 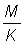 la table de valeurs de Y' (proportionnel au rendement par recrue) forme l'équivalent d'un nomogramme du rendement à partir duquel il est extrêmement facile de déterminer l'allure du rapport entre rendement et intensité de pêche ou taille à la première capture. Il convient d'agir avec circonspection lorsqu'on interprète les modifications de l'intensité de la pêche, car les valeurs sont données en fonction de
la table de valeurs de Y' (proportionnel au rendement par recrue) forme l'équivalent d'un nomogramme du rendement à partir duquel il est extrêmement facile de déterminer l'allure du rapport entre rendement et intensité de pêche ou taille à la première capture. Il convient d'agir avec circonspection lorsqu'on interprète les modifications de l'intensité de la pêche, car les valeurs sont données en fonction de 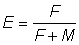 et, pour les valeurs importantes de E (au-dessus de 0,5), des variations extrêmement faibles de E correspondent à de très grandes variations de F.
et, pour les valeurs importantes de E (au-dessus de 0,5), des variations extrêmement faibles de E correspondent à de très grandes variations de F.
On peut exprimer le rendement sous d'autres formes en remplaçant, dans l'équation 9.3, le poids par diverses formules. En particulier, pour un temps relativement bref (soit t1 à t2), l'accroissement pondéral peut être traité comme valeur exponentielle, autrement dit:
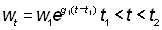
où w1 est le poids au temps t1.
Le coefficient de croissance g1 évoluera selon l'intervalle choisi, diminuant généralement à mesure qu'augmente l'âge. L'expression du rendement pondéral durant la période t1 à t2 devient:
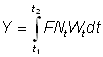
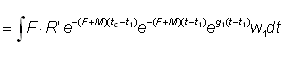
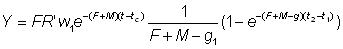
Le rendement total est alors obtenu en additionnant le rendement pour chaque fraction de vie étudiée, en utilisant un nombre d'intervalles suffisant. Cette expression de la croissance fait apparaître que la taille (ou l'âge) à laquelle la masse totale d'une classe d'âge atteint son maximum est celle pour laquelle g est égal au coefficient de mortalité naturelle M (la «taille critique» de Ricker). Le rendement maximal est donc obtenu en péchant toutes les classes d'âge dès qu'elles atteignent cette taille. Lorsque les hypothèses de l'équation simple du rendement ne sont pas satisfaites (schéma de croissance différent, paramètres non constants, etc.), il est toujours possible d'appliquer la méthode mentionnée au deuxième alinéa de la section 9.2, en exprimant le rendement comme somme des rendements d'un grand nombre d'intervalles brefs, durant lesquels lés modifications de la taille et du nombre des individus composant le stock peuvent être négligées. Autrement dit, nous obtenons une approximation de l'intégrale de l'équation 9.3 par l'expression:
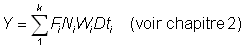
où l'intervalle de temps tc à tL à été divisé en k brefs intervalles. On a:
Fi = mortalité par pêche pendant la ième période
Ni = nombre présent au début de la ième période
Wi = poids moyen des individus durant la ième période
D ti = durée de la ième période.
On peut prendre pour Fi, une constante = F ou employer des valeurs empiriques s'il y a des indices que la mortalité par pêche varie avec l'âge. De même, Wi peut être déterminé à partir d'une courbe de croissance appropriée, ou bien on utilisera des données empiriques pour tenir compte de facteurs comme les variations saisonnières de croissance, etc.
Il est possible de calculer Ni à partir de la formule ordinaire:
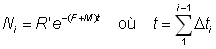
ou à partir des équations:
N1 = R'
Ni+1 = Ni - (Fi + M) Ni D ti
Il est probable que cette expression du rendement sera particulièrement utile dans toute pêcherie où ne se réalisent pas très exactement les hypothèses de la courbe simple de rendement, comme les pêcheries très saisonnières ou celles qui sont exploitées aux filets maillants, où la mortalité par pêche peut varier avec l'âge. Des études approfondies sur ordinateur ont été faites concernant les pêcheries de saumons du Pacifique, où interviennent des réglementations complexes portant sur plusieurs engins de pêche, et qui comprennent un grand nombre de stocks mélangés à des degrés divers.
A. INFLUENCES D'UNE MODIFICATION DE L'INTENSITÉ DE LA PÊCHE
A.1 Plie de la mer du Nord (maille de 75 mm)
Valeurs approximatives des paramètres (maille de 75 mm):
M = 0,1
L¥ =. 68,5 cm
W¥ = 2 860g
K = 0,095
t0 = -0,8 année
tr = 3,7 années
tc = 3,7 années
(Noter que les plies de la mer du Nord ne gagnent les principaux fonds de pêche qu'à l'âge de 3 ou 4 ans, de sorte que la taille à la première capture est indépendante du maillage jusqu'à une maille d'environ 100 mm.)
1. En utilisant la table de travail A, calculer et tracer en fonction du coefficient de mortalité par pêche (F) les courbes suivantes: poids de la population exploitée par recrue 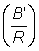 (proportionnel à la prise par unité d'effort).
(proportionnel à la prise par unité d'effort).
Rendement par recrue 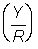 . Exprimer en grammes ainsi qu'en pourcentage du rendement actuel (autrement dit, avec F =0,5).
. Exprimer en grammes ainsi qu'en pourcentage du rendement actuel (autrement dit, avec F =0,5).
Effectif de la population exploitée par recrue 
Prises en nombre par recrue 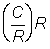 .
.
Poids moyen du poisson capturé 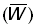
(Note: Prendre F = 0, 0,02, 0,04, 0,06, 0,08, 0,1, 0,2, 0,5, 1,0)
2. A partir des tables de fonctions de rendement (Annexe 1) et en prenant 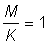 , exprimer le rendement par recrue pour chaque valeur de E des tables en pourcentage de rendement par recrue pour la valeur actuelle de E (prendre pour celle-ci 0,8). Tracer la courbe de cette valeur (a) en fonction de E et (b) en fonction de
, exprimer le rendement par recrue pour chaque valeur de E des tables en pourcentage de rendement par recrue pour la valeur actuelle de E (prendre pour celle-ci 0,8). Tracer la courbe de cette valeur (a) en fonction de E et (b) en fonction de 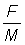 . (Note: calculer d'abord c.) Comparer la courbe 2 (b) et la courbe du rendement par recrue en fonction de l'effort obtenue à l'exercice 1.
. (Note: calculer d'abord c.) Comparer la courbe 2 (b) et la courbe du rendement par recrue en fonction de l'effort obtenue à l'exercice 1.
3. Répéter l'exercice 2 avec 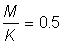 , puis 1,5.
, puis 1,5.
4. L'estimation actuelle de F pour la plie de la mer du Nord est de l'ordre de 0,5. Quel pourcentage de changement dans l'intensité de pêche par rapport au niveau actuel faudrait-il pour obtenir le rendement maximal soutenu par recrue? De quel pourcentage celui-ci diffère-t-il du niveau actuel? Quel effet ce changement de l'intensité de la pêche aurait-il sur la prise par unité d'effort et sur le poids moyen du poisson capturé? Dans quelle mesure ces réponses dépendent-elles de la valeur de M?
5. Répéter l'exercice pour une maille de 140 mm, étant donné que pour cette dimension de maille tc = 5,5 années.
A.2 Eglefin dé là mer du Nord (maille de 75 mm)
Valeurs approximatives des paramètres (maille de 75 mm);
M = 0,2
L¥ = 55 cm
W¥ = 1 300g
K = 0,25
t0 = -0,2 année
tr = 1,0 année
tc == 2,1 années
1. Effectuer les mêmes calculs qu'en A.1 et 2 ci-dessus. Note: Estimation actuelle de F pour l'églefin de la mer du Nord: environ 0,8; dans les tables de rendement, prendre 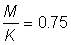 .
.
2. Répéter l'exercice avec 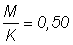 , puis 1,25.
, puis 1,25.
3. Répéter l'exercice pour une maille de 100 mm, avec tc = 3,3 années.
B. INFLUENCES D'UNE MODIFICATION DU MAILLAGE
B.1 Plie de la mer du Nord (F = 0,5)
1. Pour les mailles supérieures à 120 mm, la longueur moyenne de sélection lc peut être calculée directement à partir du facteur de sélection (b) = 2,2. En utilisant les tables de travail B.1 et B.2, avec F = 0,5, calculer et tracer en fonction du maillage les courbes 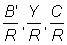 et
et 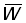 . Prendre M =0,1 et les autres valeurs de paramètres comme en A.1. Exprimer le rendement en pourcentage du rendement actuel, autrement dit pour une maille de 75 mm. (Note: prendre comme dimensions de maille 120, 160, 180, 200, 220, 240 et 260 mm. Tracer aussi les valeurs précédemment calculées avec F =0,5 pour les mailles de 75 et de 140 mm.
. Prendre M =0,1 et les autres valeurs de paramètres comme en A.1. Exprimer le rendement en pourcentage du rendement actuel, autrement dit pour une maille de 75 mm. (Note: prendre comme dimensions de maille 120, 160, 180, 200, 220, 240 et 260 mm. Tracer aussi les valeurs précédemment calculées avec F =0,5 pour les mailles de 75 et de 140 mm.
2. Utiliser les tables de rendement pour 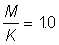 afin de déterminer l'allure de la courbe du rendement par recrue en fonction de la dimension de maille. Répéter avec
afin de déterminer l'allure de la courbe du rendement par recrue en fonction de la dimension de maille. Répéter avec 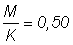 , puis 1,5 (calculer d'abord E et utiliser la valeur de E des tables la plus proche).
, puis 1,5 (calculer d'abord E et utiliser la valeur de E des tables la plus proche).
3. Quelle dimension de maille faut-il pour obtenir le rendement maximal soutenu par recrue avec cette valeur de F? De quel pourcentage celui-ci diffère-t-il du niveau actuel? Quels seraient les changements correspondants de la prise par unité d'effort et du poids moyen des poissons capturés? Dans quelle mesure ces réponses dépendent-elles de la valeur de M?
4. Répéter les exercices 1 à 3 ci-dessus, mais en prenant la valeur F = 0,2. Comparer vos résultats et conclusions avec ceux qu'avait donné F = 0,5.
B.2 Eglefin de la mer du Nord (F = 0,8)
1. Le rapport entre la longueur moyenne de sélection lc et la dimension de maille pour l'églefin peut être calculée avec un facteur de sélection de 3,2. En utilisant les tables de travail B.1 et B.2, F étant égal à 0,8,
calculer et tracer en fonction du maillage les courbes 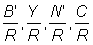 et
et 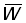 . Prendre pour les paramètres les valeurs données ci-dessus en A.2. (Note: prendre comme dimensions de maille 80, 90, 120, 140, 150 et 160 mm. Tracer aussi les valeurs précédemment calculées pour des maillages de 75 et de 100 mm avec F = 0,8).
. Prendre pour les paramètres les valeurs données ci-dessus en A.2. (Note: prendre comme dimensions de maille 80, 90, 120, 140, 150 et 160 mm. Tracer aussi les valeurs précédemment calculées pour des maillages de 75 et de 100 mm avec F = 0,8).
2. Utiliser les tables de rendement pour déterminer l'allure de la courbe du rendement par recrue en fonction du maillage pour 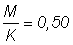 , 0,75 et 1,25 (prendre E=0,85, 0,80, 0,70).
, 0,75 et 1,25 (prendre E=0,85, 0,80, 0,70).
3. Quelle dimension de maille faut-il pour obtenir le rendement maximal soutenu par recrue avec cette valeur de F? De quel pourcentage celui-ci diffère-t-il du niveau actuel? Quels seraient les changements correspondants de la prise par unité d'effort et du poids moyen des poissons capturés? Dans quelle mesure ces réponses dépendent-elles de la valeur de M?
4. Répéter les exercices 1 à 3 ci-dessus mais en prenant la valeur F =0,3, Comparer vos résultats et conclusions avec ceux qu'avait donné F = 0,8 et avec ceux qui avaient été obtenus pour la plie de la mer du Nord.
TABLE DE TRAVAIL A. - Évaluations de l'intensité de la pêche
TABLE DE TRAVAIL B.1. - Évaluations du maillage (1)
TABLE DE TRAVAIL B.2. - Évaluations du maillage (2)