10. ÉVALUATIONS SPÉCIALES

10.1 Statistiques des prises et de l'effort de pêche
10.2 Modèle de Schaefer
10.3 Modifications de la sélectivité
10.4 Interaction de pêcheries
10.5 Exercices

L'équation simple de production décrite au chapitre précédent dépend pour son calcul d'une connaissance assez complète des divers paramètres (croissance, mortalité, etc.), information permettant d'estimer le rendement soutenu pour toute combinaison de mortalité par pêche et d'âge à la première capture. Cependant, même si - comme cela arrive très souvent - l'information est loin d'être complète, il est possible de répondre à certaines questions - par exemple: un accroissement modéré de la taille à la première capture aurait-il pour effet d'augmenter ou de diminuer le rendement soutenu?

10.1 Statistiques des prises et de l'effort de pêche

Si l'on dispose de statistiques pour plusieurs périodes pendant lesquelles l'effort de pêche s'est maintenu à un niveau constant, il est évidemment possible d'en tirer une relation purement empirique entre effort de pêche et rendement soutenu, ou prise par unité d'effort (p.u.e.). Dans la plupart des pêcheries, il est rare que l'on exerce durant de longues périodes un effort de pêche constant, et tant captures que p.u.e. pour une année donnée seront liées non seulement à l'effort durant cette année mais à l'effort de plusieurs années antérieures. Cependant, l'abondance d'une certaine classe d'âge se trouvant dans la pêcherie pendant par exemple quatre années (autrement dit d'âge t_c + 4) sera déterminée par un facteur égal à 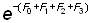, où F₀, F_1, F₂ et F₃ sont les mortalités par pêche pendant les quatre années précédentes; autrement dit, l'abondance de cette classe d'âge sera la même que si elle s'était trouvée dans une pêcherie accusant une mortalité par pêche régulière de 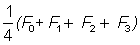. La p.u.e. totale de tous âges est alors reliée à une moyenne pondérée de l'effort de pêche durant le; années précédentes. Si cette moyenne est calculée sur une période égale à la durée moyenne de la vie dans la phase exploitée (par exemple si l'âge au recrutement est de 4 ans, et le gros de la prise pondérale constitué de poissons entre 4 et 9 ans, la durée moyenne est d'environ 3 ans), alors le rapport entre cet effort moyen (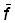) et la p.u.e. sera proche de celui qui existe entre effort et p.u.e. dans l'hypothèse d'une situation stable. En fait, la concordance sera presque exacte, non seulement quand l'effort n'a pas beaucoup évolué, mais aussi lorsqu'il a manifesté une tendance marquée. Par exemple, si l'effort s'est accru, les âges les plus vieux seront surabondants, l'effort de pêche moyen exercé sur eux ayant été inférieur à 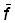, tandis que les plus jeunes seront trop rares, puisqu'ils auront subi un effort moyen supérieur à .

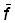C'est graphiquement que cette relation s'exprime le mieux, en portant la p.u.e. en fonction de 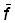. La meilleure forme n'est généralement pas une droite, mais une courbe à concavité tournée vers le haut (comme les courbes relatives aux plies et aux cabillauds en Islande (Gulland, 1961 b). Connaissant le rapport existant entre p.u.e. et effort dans l'hypothèse d'une situation stable, le rapport correspondant entre prise et effort peut être déduit immédiatement de cette courbe par multiplication.

Cette approximation est très proche du modèle à paramètres constants de la courbe complète de rendement, dans laquelle les effets dépendant de la densité sont négligés, puisque la plupart d'entre eux s'exercent sur de plus longues périodes. Par exemple, dans le cas ci-dessus, si le recrutement est affecté, le stock actuel est constitué par les descendants du stock qui existait en moyenne de 6 à 7 ans auparavant, lequel avait été déterminé par la pêche exercée durant les 3 années antérieures ou davantage.

Principal avantage de cette méthode: les données qu'elle exige sont faciles à obtenir, car la prise totale est généralement connue, et l'effort ou la p.u.e. sont généralement parmi les premières données semi-scientifiques à être recueillies. S'il y a des erreurs dans les renseignements sur l'effort (les plus probables étant des tendances non corrigées, comme un accroissement de l'efficacité), elles affecteront à la fois les valeurs de x et de y dans le graphique, et tendront à déplacer les points le long des lignes de l'équation y = a/x. Ce mouvement ayant lieu dans la même direction que l'allure générale de la régression attendue, les erreurs dans la mesure de l'effort ne fausseront pas l'estimation de la relation p.u.e./effort, quoiqu'elles puissent rendre la signification statistique de l'ajustement plus grande qu'elle ne l'est réellement. Si la série de données est assez longue, on pourra étudier les incidences de modification autres que celles qui portent simplement sur l'effort total. Ainsi, s'il y a eu un changement dans les pratiques de pêche (par exemple accroissement de la dimension de maille) au milieu de la série, on pourra, si cette modification a eu un effet significatif sur le stock, déterminer deux régressions différentes de la p.u.e. sur l'effort pour les périodes se situant avant et après le changement.

10.2 Modèle de Schaefer

Une autre méthode d'analyse dépendant principalement des données sur les captures et sur l'effort de pêche est celle de Schaefer, 1954, 1957. La biomasse de la population B est considérée comme une unique entité qui, si la pêche n'avait pas lieu, augmenterait à un taux déterminé par sa taille:

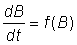
où f (B) est une fonction de B qui est nulle lorsque B = 0 ou atteint son maximum B_M, et maximale pour une valeur intermédiaire de B.

Par conséquent, quand il y a pêche:

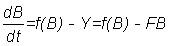
où Y == prise.

Il est évident que la population demeurera constante si Y = f (B), de sorte qu'à chaque taille de la population correspondra une certaine prise équilibrée, qui sera maximale quand f (B) est au maximum.

La forme de f (B) peut être déterminée à partir de données sur les prises et sur l'effort de pêche, à condition de disposer également de renseignements (par exemple obtenus par marquage) à partir desquels les chiffres de la p.u.e. peuvent être convertis en termes absolus - autrement dit si l'on connaît le coefficient q (k₂ dans la notation de Schaefer). Ainsi, si les valeurs de la p.u.e. sont connues au début et à la fin de l'année, on peut écrire:

On a alors: B₂ - B₁ = modification de la population 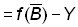ou 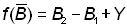, où y est la prise pendant l'année.

On ne connaît généralement pas la p.u.e. au début de l'année, mais sa valeur moyenne pour l'ensemble de l'année. La p.u.e. au début de l'année peut être estimée comme moyenne des captures moyennes par unité d'effort durant les 12 mois antérieurs et ultérieurs. On peut donc obtenir une paire de valeurs 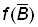de et de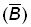 pour chaque année, et, en reportant l'une en fonction de l'autre, établir la relation entre la «prise équilibrée» et la taille du stock. Le tracé se fera plus rapidement si l'on fait une hypothèse sur la forme de f (B), par exemple l'équation:

f (B)= aB (B_M - B)

qui, en fonction de B, donne une parabole. Le meilleur ajustement s'obtient tient en portant 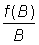en fonction de B, ce qui donne une ligne droite. Cette méthode d'analyse a beaucoup de points communs avec celle qui est exposée au chapitre précédent. Les deux méthodes visent à obtenir la relation d'équilibre entre prise et effort (ou l'une de ses transformations) par un ajustement approprié des données relatives à une pêcherie en évolution - l'une en tenant compte des données sur l'effort durant les années précédentes, et l'autre des modifications de la p.u.e. Ce modèle présente des avantages du point de vue de la simplicité et n'exige que peu de données. En outre, il semble plus conforme à la situation réelle des populations naturelles que le modèle analytique étudié au chapitre précédent, du moins dans la mesure où celui-ci ne tient pas compte des modifications éventuelles des divers paramètres (croissance, mortalité et recrutement) liées à l'évolution de l'abondance de la population.

Toutefois, ces avantages sont essentiellement superficiels. Le modèle analytique peut être remanié pour tenir compte des complexités de toute population naturelle, tandis que le modèle de Schaefer se prête mal aux modifications. De plus, le taux naturel d'accroissement d'une population n'est pas déterminé uniquement par la biomasse à un moment donné. Le recrutement dépend (en dehors des facteurs ambiants) de ce qu'était le stock adulte à un certain moment, qui peut remonter à plusieurs années. L'accroissement de la biomasse de la population dû à la croissance, exprimé absolument ou en pourcentage de la biomasse actuelle, repose autant, sinon davantage, sur la pyramide des âges de la population que sur sa biomasse totale. Pour pouvoir tenir compte de ces éléments, il est indispensable d'utiliser un modèle analytique.

10.3 Modifications de la sélectivité

La plus élémentaire et peut-être la plus importante question soulevée par les incidences d'une modification éventuelle de la sélectivité est celle de savoir si le changement produira un accroissement ou une diminution de la prise moyenne. L'estimation peut se faire, comme l'a montré Allen (1953), en établissant un rapprochement entre le poids moyen du poisson de la taille que l'on désire laisser fuir et la probabilité que ce poisson soit capturé ultérieurement, et son poids moyen dans cette éventualité. Autrement dit, si l'on a:

W_c = poids du poisson à la longueur moyenne de sélection
= poids moyen du poisson figurant dans les captures et supérieur à W_c

la prise sera alors accrue si le poisson peut s'échapper du filet lorsque 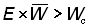où E= probabilité qu'un poisson ayant fui soit repris plus tard si la mortalité par pêche et la mortalité naturelle sont constantes. Ou bien encore, si l'on utilise le rapport pêche/mortalité totale, on aura accroissement de la prise si 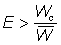. Le membre de droite de cette inégalité peut être aisément calculé à partir d'observations simples sur la composition par taille des captures.

On peut également déterminer des incidences plus détaillées de modifications de la sélectivité à partir de connaissances sur la composition par taille des apports (voir Gulland, 1961a, 1964a). Ainsi, juste après une modification de l'engin de pêche, il n'y aura pas de changement dans le stock, et le nombre de poissons d'une taille donnée/débarqués par le nouvel engin (par exemple à dimension de maille plus grande) sera donné par:

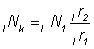, (10.1)

où

_lN₁ = nombre capturé par l'ancien engin de pêche
_lN_k, = nombre capturé par le nouvel engin;/
_lr₁ = proportion retenue par l'ancien engin;
_lr₂ == proportion retenue par le nouvel engin

Si l'on a aussi _lW = poids moyen du poisson de longueur l, alors le poids total W₁ pris par l'ancien engin est donné par la formule:

W₁ =S _lW_lN₁, (10.2)

et le poids capturé par le nouvel engin, W_k, par:

W_k=S _lW_lN_k, (10.3)

En outre, le nombre total pris par l'ancien engin N₁ et retenu par le nouvel engin (N_k) peut être exprimé par la formule:

N₁ = S _lN₁, et N_k = S _lN_k

(Si les poids moyens _lW et les nombres y relatifs sont rangés en colonnes parallèles, ces calculs de sommes de produits sont faciles à effectuer sur la plupart des machines à calculer.) Le changement réel et immédiat dans les mises à terre peut être exprimé comme une proportion L des apports initiaux, soit:

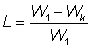
Quand un accroissement dans la longueur moyenne de sélection a lieu, les poissons relâchés par le nouvel engin, mais qui auraient pu être pris par l'ancien, grandiront et, après un certain temps, atteindront la taille à laquelle ils seront retenus par le nouvel engin, et les captures augmenteront alors.

Le nombre de poissons relâchés (N_R) qui auraient précédemment été capturés sera égal à N₁ - N_k. Si des quantités de petits poissons sont capturés et rejetés à la mer, le nombre total relâché sera supérieur à la diminution des apports, et pourra être calculé par la formule:

, (10.4)

où _lN_c représente le nombre de poissons de longueur l pris par l'ancien engin, y compris la pêche rejetée. Sur ces poissons, un nombre 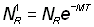survivra jusqu'à ₂t_c âge moyen à la première capture avec le nouvel engin, formule dans laquelle T est la différence entre ₂t_c et l'âge moyen des poissons ayant pu s'échapper. Sur ces poissons, un nombre sera en définitive capturé, E étant le taux d'exploitation (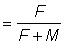 quand les mortalités sont constantes). Comme toutes les mortalités, etc., pour les poissons plus grands que ₂l_c sont inchangées, la distribution par taille de ces poissons sera la même que pour les poissons N_k, de sorte qu'au bout d'un certain temps les captures avec le nouvel engin seront augmentées d'une proportion Q, avec:

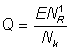, (10.5)

Ainsi, les apports à long terme, W₂, seront donnés par:

W₂ = W₁ (1 - L)(1+Q), (10.6)

Ces apports pourront n'être atteints que plusieurs années après la modification de la sélectivité. Le niveau ne sera réalisé qu'au terme d'une période égale à la longévité du poisson dans la pêcherie et commençant à la date du changement, mais une valeur proche sera atteinte avant cette échéance. Voici comment on peut estimer les prises durant cette période intermédiaire. Pour évaluer les débarquements au temps t', supposons que les poissons relâchés ont atteint une certaine longueur l'.

A un instant t' après la modification du maillage, les poissons plus grands que l' auraient été péchés par l'ancienne maille lorsque leur taille tombait dans la zone de sélection, de sorte que le stock et les prises de ces poissons ne seront pratiquement pas affectés par la modification, et la capture pondérale des poissons de longueur l > l' sera _lW_lN_R. Les poissons plus petits que l' auraient subi l'effet du nouveau maillage durant leur vie dans la phase exploitée, de sorte que le stock et les prises de ces tailles pourraient être les mêmes que dans l'état d'équilibre à long terme réalisé avec la nouvelle maille, et la capture pondérale de poisson de longueur l < l' serait égale à (1 + Q) _lW_lN_R.

La prise pondérale totale sera W', donné par la formule:

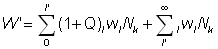
c'est-à-dire:

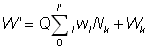, (10.7)

La méthode peut être étendue aux stocks exploités par plusieurs engins, dont certains peuvent ne pas changer de sélectivité. Dans ce cas, on appliquera séparément à chaque flotte les équations 10.1 et 10.3 pour obtenir les effets immédiats. Le facteur Q sera le même pour toutes, et sa valeur est donnée par l'extension de l'équation 10.5 sous la. forme:

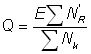, (10.8)

où la sommation de N_k comprend les poissons capturés par tous les engins (à l'exception des poissons pris par les engins dont la sélectivité ne change pas et plus petits que la nouvelle longueur de sélection), mais la sommation de N_R, naturellement, ne comprend que les engins dont la sélectivité change. La table de travail reproduite à la page suivante indique les calculs nécessaires pour évaluer les résultats d'une modification de maillage en cas d'emploi simultané de deux engins pouvant capturer des poissons de tailles différentes.

10.4 Interaction de pêcheries

Les méthodes ci-dessus peuvent servir aussi pour étudier l'interaction de diverses pêcheries, et notamment le cas d'une pêcherie A portant essentiellement sur une espèce (par exemple hareng) mais capturant accessoirement de jeunes poissons d'une autre espèce (par exemple églefin) qui, lorsqu'ils sont plus âgés, font eux-mêmes l'objet principal d'une pêcherie B.

TABLE DE TRAVAIL C. - Evaluation des modifications de la sélectivité (pour deux engins de pêche dont les prises présentent des compositions par taille différentes)

1^re partie. - Effets immédiats

2^e partie. - Effets à long terme

NR: Nombre de poissons échappant aux engins	NK: Nombre de poissons capturés immédiatement après la modification
Engin A	Engin A
Engin B	Engin B
Pêche rejetée: ___	Engins non visés par les règlements:___
Total:___	Total: ___

T =	M T =
e-MT

			Engin A		Engin B
E	Q	1 +Q	(1 - L) (1 + Q)	G	(1 - L) (1 + Q)	G

G = 1- (1-L)(1+Q)

On procède comme suit:

1. Calculer le nombre de poissons capturés par la flotte A, ou le nombre supplémentaire capturé par rapport à ce que seraient les prises de cette flotte si elle se conformait à un certain règlement envisagé (=N).

2. Calculer le nombre réduit de ces poissons qui survivront jusqu'à l'âge de la première capture par la flotte B (=N¹)

3. Comparer le nombre de ces poissons (=EN¹) qui serait capturé avec la prise actuelle, C, de la flotte B. L'augmentation des prises de la flotte B qui aurait lieu si la flotte A cessait de pêcher est alors, en proportion de la prise actuelle,.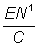

Le même résultat pourrait être obtenu en comparant N¹ avec le nombre de poissons «recrutés» par la flotte B, qui est égal à 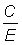(voir CIEM, 1960).

10.5 Exercices

1. Le tableau ci-après donne la p.u.e. ou prise par unité d'effort (prise en tonnes par millier d'heures-tonneau des chalutiers britanniques) et la prise totale (en milliers de tonnes) de cabillauds et d'églefins en Islande.

a) Calculer l'effort de pêche total annuel en unités anglaises, pour le cabillaud et l'églefin.

b) Si la durée moyenne de vie dans la pêcherie est de deux ans pour l'églefin et de trois pour le cabillaud, relier l'abondance du stock à l'effort de pêche passé. Existe-t-il des indices qu'un de ces rapports ait changé? En particulier, examiner la courbe relative à l'églefin depuis 1950, année d'introduction d'une dimension de maille plus grande et d'interdiction du chalutage dans certains secteurs, comprenant des zones de rassemblement des jeunes.

2. Le tableau de la page 135 renferme des données sur les captures et la p.u.e. de baleines bleues dans l'Antarctique. En prenant successivement pour valeur de l'effectif de la population correspondant à une p.u.e. de 1,00 les chiffres de 20 000 et de 30 000, calculer la modification annuelle de l'effectif de la population, puis le rendement soutenu pouvant être escompté chaque année. La tracer en fonction de la taille de la population cette année-là et cinq ans plus tôt (en supposant que les baleines bleues atteignent la phase exploitée à l'âge de 5 ans).

Année	Prise totale		p.u.e.		Année	Prise totale		p.u.e.
	Cabillaud	Eglefin	Cabillaud	Eglefin		Cabillaud	Eglefin	Cabillaud	Eglefin
1906	105	35	0,97	0,55	1936	280	25	1,14	0,14
1907	115	30	1,03	0,49	1937	295	25	1,39	0,11
1908	125	31	1,20	0,54	1938	305	24	1,11	0,16
1909	115	28	1,05	0,57	1939	198	13
1910	135	30	1,12	0,56	1940	148	20
1911	155	31	1,26	0,58	1941	158	15
1912	160	28	1,20	0,47	1942	176	17
1913	180	26	1,27	0,38	1943	189	13
					1944	220	12
1919	130	35	1,41	1,01	1945	216	14
1920	190	53	1,39	0,70	1946	237	28	1,84	0,63
1921	175	37	1,16	0,58	1947	246	33	1,46	0,42
1922	220	40	1,27	0,61	1948	293	52	1,27	0,32
1923	220	38	1,09	0,44	1949	315	66	1,17	0,37
1924	300	38	1,09	0,30	1950	321	60	0,98	0,24
1925	320	35	1,28	0,31	1951	327	54	0,94	0,19
1926	295	37	1,09	0,32	1952	392	45	0,91	0,18
1927	340	54	0,99	0,38	1953	515	53	1,11	0,18
1928	360	57	0,88	0,34	1954	546	62	1,01	0,17
1929	390	54	0,83	0,29	1955	537	64	1,04	0,21
1930	490	49	1,10	0,28	1956	482	62	1,02	0,19
1931	475	40	1,09	0,21	1957	453	76	0,81	0,16
1932	480	32	1,34	0,19	1958	511	70	0,80	0,14
1933	510	26	1,28	0,14	1959	454	64	0,68	0,18
1934	480	26	1,14	0,14	1960			0,64	0,18
1935	400	27	1,16	0,14

Comment peut-on utiliser les données sur la prise pour les années 1939-46?

Quel est le rendement maximal soutenu, et à quel effectif de population correspond-il?

3. Le tableau de la page 136 contient des données sur la pêche britannique au chalut de l'églefin (îles Féroé), avec le nombre débarqué par catégories de 5 cm de longueur, le poids moyen, et la proportion de chaque groupe retenue par une maille de 90 mm et par une maille de 120 mm.

a) Quel est le poids total débarqué?

b) En supposant que le maillage actuel soit de 90 mm, quelle serait la diminution de prise (en pourcentage) dès l'introduction d'une maille de 120 mm?

c) S'il faut en moyenne six mois aux poissons échappant au filet pour atteindre la taille de première capture par la maille de 120 mm, quel serait l'effet à long terme d'un accroissement de la maille à 120 mm, en supposant qu'il n'y a pas d'autre pêcherie et que la mortalité naturelle du poisson à la taille de sélection est de 0,2, et que E (=F/F+M)=0,5?

Année	Prise totale	P.u.e.
1925/26	4 697	3,30
1926/27	6 545	3,76
1927/28	8 334	4,39
1928/29	12 734	4,49
1929/30	17 898	3,13
1930/31	29 410	3,71
1931/32	6 488	4,83
1932/33	18 890	4,61
1933/34	17 349	4,76
1934/35	16 500	3,46
1935/36	17 731	3,96
1936/37	14 304	2,83
1937/38	14 923	2,00
1938/39	14 081	1,77
1939/40	11 480
1940/41	4 943
1941/42	59
1942/43	125
1943/44	339
1944/45	1 042
1945/46	3 606	1,36
1946/47	9 192	1,85
1947/48	6 908	1,12
1948/49	7 625	0,98
1949/50	6 182	0,80
1950/51	7 048	0,81
1951/52	5 130	0,63
1952/53	3 870	0,44
1953/54	2 697	0,42
1954/55	2 176	0,31
1955/56	1 614	0,37
1956/57	1 512	0,27
1957/58	1 690	0,28
1958/59	1 187	0,18
1959/60	1 228	0,14
1960/61	587*	0,105
1961/62	639*	0,093

* A l'exception des baleines bleues naines.

Longueur	Poids moyen	Pourcentage retenu		Nombre débarqué
cm	g	90 mm	120 mm	Milliers
25-29	160	50	3	8
30-34	260	80	16	314
35-39	420	98	41	1 084
40-44	630	100	72	1 409
45-49	880	100	94	1 370
50-54	1 190	100	100	952
55-59	1 570	100	100	465
60-64	1 760	100	100	255
65-69	2 530	100	100	124
70-74	3 100	100	100	73
75-79	3 800	100	100	30
80+	4 600	100	100	9

d) Quels seraient les effets à long terme sur les deux pêcheries (en pourcentage et en poids réel) s'il existait également une pêcherie aux lignes prenant annuellement une moyenne de 5 millions de poissons (représentant un poids de 6000 tonnes), avec E=0,7? (supposer que tous les poissons pris aux lignes sont plus grands que la taille de sélection correspondant à la maille de 120 mm.)

e) Quel serait l'effet si les chalutiers rejetaient à la mer 30 pour cent (en nombre) de leur prise, et si ces poissons étaient tous assez petits pour échapper à une maille de 120 mm? (Avec par exemple T = un an).

4. Prise annuelle moyenne d'églefins par des chalutiers péchant le hareng en 1954-56:

Taille	Prise	Poids débarqué	Nombre de poissons
Moins de 24 cm	................ Tonnes................		Millions 25
	2 500	-
De 24 à 27 cm	6 000	-	45
Plus de 27 cm	23 500	14000	80
Total	32 000	14 000	150

La pêcherie d'églefins débarque en moyenne 70 000 tonnes par an (poids moyen du poisson: 330 grammes). Si l'on utilisait pour le chalutage du hareng la dimension de maille minimale imposée pour le poisson de fond, quel serait l'effet sur les prises d'églefins, en supposant:

a) Que la maille légale laisse échapper tous les églefins de taille inférieure à 24 cm;

b) Que dans la pêcherie d'églefins on capture une centaine de millions de poissons de plus de 24 cm, qui sont rejetés parce qu'ils n'atteignent pas la taille marchande de 27 cm;

c) Qu'il faut aux poissons de moins de 24 cm échappant à une maille plus grande une moyenne de 6 mois pour atteindre 24 cm, époque durant laquelle ils subissent une mortalité naturelle de 0,2;

d) Que (où F comprend tous les modes de pêche).