Dans le chapitre précédent, tous les paramètres (croissance, mortalité, etc.) ont été supposés constants, à l'exception des variations explicites de la mortalité par pêche ou de l'âge à la première capture. En fait, tous les paramètres peuvent changer, et certains d'entre eux, comme le recrutement annuel, même dans de très fortes proportions. La variation peut être le résultat, direct ou indirect, de modifications de l'abondance du stock (d'où la possibilité d'une influence de la pêche), ou être indépendante du stock, et provenir alors de changements survenus dans le milieu - quantité de nourriture disponible, etc. Ces derniers peuvent être divisés en deux catégories, selon l'effet produit: (a) modifications altérant la forme des courbes de production, de sorte que les résultats, par exemple d'un accroissement du maillage, peuvent être quantitativement différents; (b) modifications n'affectant que la hauteur de la courbe de production, et pouvant alors dans de nombreux cas être négligées.
Le meilleur exemple de la seconde catégorie est la forte variation pouvant intervenir, indépendamment des fluctuations de l'effectif du stock adulte frayant, dans l'abondance des classes d'âge successives chez de nombreux poissons - églefin, hareng, etc. Des calculs négligeant les données sur la modification des classes d'âge pourraient faire conclure qu'à un relèvement du maillage moyen (par exemple de 100 à 110 mm) correspondrait par exemple un accroissement de l'ordre de 5 pour cent du rendement soutenu. Mais il ne s'ensuit pas que, si la dimension de maille augmente, le rendement dans n'importe quelle année à venir sera exactement de 5 pour cent plus élevé que le rendement actuel, car les classes d'âge qui seront alors pêchées pourront présenter une tout autre abondance. Ce qui est vrai (si les calculs sont corrects), c'est que la production sera supérieure de 5 pour cent à ce qu'elle aurait été si l'on avait conservé l'ancienne maille de 100 mm. Pour résoudre maintes questions d'ordre pratique (par exemple est-il souhaitable de porter le maillage de 100 à 110 mm?), les différences dues aux variations du recrutement ne présentent guère d'importance. Pour ce motif, et parce que, comme on l'a vu aux chapitres précédents, c'est la forme sous laquelle on exprime souvent la production, de nombreuses évaluations sont formulées en rendement par recrue. La règle connaît une exception quand l'intensité de la pêche dépend de manière critique de l'effectif des classes d'âge présentes dans la pêcherie, car il n'y a que peu ou pas du tout de pêche lorsque les classes d'âge sont faiblement représentées. Un bon exemple est fourni par la pêcherie d'églefins du banc de Saint Pierre, où de 1953 à 1957 une très forte pêche s'est exercée aux dépens de l'exceptionnelle classe d'âge 1949, alors que l'on a très peu péché avant et après cette période.
Les modifications intervenant dans la croissance peuvent influer sur l'allure des courbes de rendement, notamment celle qui exprime la production en fonction de la taille à la première capture. Dans un stock fortement péché, le rendement maximal peut correspondre à une taille à la première capture (lc) peu inférieure à la taille maximale (L¥ ), mais s'il y a un changement dans la croissance, avec une valeur nouvelle et inférieure de L¥ il est possible que peu de poissons survivent jusqu'à la taille lc, et le rendement pour cette valeur de lc risque d'être faible.
Si certaines modifications du milieu peuvent signifier que les courbes de rendement n'auront pas à l'avenir la même allure que maintenant, les effets liés à la densité peuvent avoir pour conséquence que la courbe de production réelle diffère de celle que l'on obtiendrait par le calcul en supposant les paramètres constants. Si le stock s'accroît, par exemple à la suite d'une diminution de la pêche, il en résultera probablement une augmentation de la mortalité naturelle et une diminution de la croissance, mais aussi un relèvement du recrutement. Ces effets agissent en sens inverse, les deux premiers réduisant la valeur de la production pour de forts effectifs du stock (par exemple à de faibles intensités de pêche, ou pour une grande dimension de maille), mais le dernier faisant croître la production pour ces mêmes conditions de pêche. Dans le cas d'un stock intensément péché, où l'on pourrait s'attendre à ce que la diminution de la pêche ou l'accroissement du maillage augmente le rendement, mortalité dépendant de la densité et croissance exercent une action d'«amortissement», tendant à aplatir la courbe de rendement, mais le recrutement aura pour effet d'exagérer les changements. C'est pourquoi le recrutement qui est fonction de la densité constitue l'effet le plus critique.
Si l'on peut établir une relation entre un paramètre quelconque et l'abondance du stock, on peut l'inclure dans l'équation simple de rendement. Il est généralement impossible de donner une expression mathématique explicite du stock ou du rendement quand un paramètre évolue avec la densité du stock, mais on peut obtenir des estimations du stock et de la production pour toute condition donnée d'effort de pêche, etc., par approximations successives. Par exemple, si la mortalité naturelle est proportionnelle à l'abondance du stock, on peut, pour calculer le rendement et le stock à un niveau de pêche égal par exemple au double de l'actuel, prendre une première estimation de la moitié du stock - autrement dit avec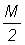 
. En utilisant cette valeur de M dans les équations, on obtiendra une meilleure estimation du stock, et donc de M, qui pourra à son tour servir à perfectionner les estimations.
En fait, il est fréquemment impossible de déterminer l'influence sur les divers paramètres, et plus particulièrement sur la mortalité naturelle, des effets dépendant de la densité, et la meilleure façon de procéder consiste probablement à prendre certaines relations vraisemblables et à voir comment elles agissent sur l'allure de la courbe de rendement (voir Beverton et Holt, 1957, chapitre 18).
Dans l'étude de l'incidence sur le recrutement, deux valeurs peuvent être reliées à l'importance du stock: recrutement (nombre absolu de jeunes poissons produits par un stock donné) et survie (nombre de jeunes par million d'œufs pondus). Si, comme on le suppose parfois, le recrutement est constant, au moins sur l'ensemble des tailles probables du stock, l'utilisation de ces deux rapports peut indiquer si une relation non significative (au sens statistique) entre stock et recrutement est due à une modification réelle et significative (au sens biologique et pratique) du recrutement par rapport à l'abondance du stock qui serait voilée par des variations des données, ou bien si le recrutement moyen est vraiment constant. On devrait pouvoir déceler le second cas par l'existence d'un rapport entre survie et recrutement.
Le stock de reproducteurs de plies de la mer du Nord peut être évalué par la prise pondérale par 100 heures de pêche des chalutiers britanniques, et le recrutement par la prise (en nombre par heure) de poissons de quatre ans quatre années plus tard. Le tableau ci-après indique les données disponibles pour certaines années (d'après Beverton, 1962).
|
Année |
Stock |
Recrutement |
Année |
Stock |
Recrutement |
|
cwt* |
cwt** |
||||
|
1926 |
16 |
18 |
1943 |
120 |
18 |
|
1927 |
15 |
28 |
1944 |
140 |
16 |
|
1928 |
16 |
61 |
1945 |
150 |
33 |
|
1929 |
16 |
36 |
1946 |
76 |
32 |
|
1930 |
17 |
27 |
1947 |
54 |
45 |
|
1931 |
16 |
18 |
1948 |
44 |
22 |
|
1932 |
16 |
28 |
1949 |
35 |
20 |
|
|
|
|
1950 |
33 |
23 |
|
|
|
|
1951 |
31 |
9 |
|
|
|
|
1952 |
32 |
22 |
* 1 hundredweight (cwt) = 50,802 kg.
En supposant le nombre d'œufs proportionnel à l'importance du stock, calculer un indice de survie depuis l'œuf jusqu'au recrutement. Quel est le rapport (a) entre stock et recrutement? (b) entre stock et survie?
