9.1 Derivation of the equation for yield
9.2 Other forms of the yield equation
9.3 Exercises
Previous sections have been concerned with methods of collecting the basic data, and analysing them so as to obtain estimates of the basic population parameters - growth, mortality, age at recruitment, etc. This and later sections will be concerned with using these estimates to explain and understand the past history of the fishery, and to predict its future; in particular to predict the effect of changes in the pattern of fishing due to any proposed conservation or regulatory measure.
The simplest calculations are for a stock in which the various parameters are constant. For such a stock, the calculations are best made in terms of the yield of a single year-class of fish throughout its life, which will be, in the steady state, the same as the yield in one year from all year-classes present in the fishery. The whole life span can be divided into relatively short periods; for each period the number of fish alive, the number caught, the number dying of natural (nonfishery) causes, and the number surviving to the beginning of the next period can be calculated, and the yield, in weight, can be calculated as the product of the numbers caught and their average weight. This process can be done purely arithmetically, but for accuracy the periods chosen should be short, and therefore numerous, and the calculations are bound to be laborious. It is much easier to express the yield in an algebraic form, which has the great advantage of showing explicitly the influence of the various parameters on the yield.
We will define the terms as follows:
Nt = number of fish alive at age t
R == number of recruits, i.e. the number of fish alive at age tr,
R' = number of fish alive at the age tc at which they are first retained by the gear in use
M = instantaneous natural mortality coefficient
F = instantaneous fishing mortality coefficient;
then for tc < t <tc
i.e., the instantaneous rate at which fish are dying of natural causes is equal to the product of the natural mortality coefficient times the number of fish.
and
and for t > tc, when both fishing and natural mortalities are operating
and
.................. (9.1)
or
The numbers of fish caught in the time interval (t, t + dt) will be F · Ntdt, so that the total numbers caught, C, will be given by dividing up the total time between tc (the age at first capture) and tL (the maximum age attained) into short intervals, and adding the contributions from each interval.
Mathematically this is expressed by the integral (see section 2)
or, integrating
.............................. (9.2)
which, if tL is sufficiently large for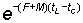 
to be neglected, reduces to
..............................(9.2')
Thus, fishing takes a share of the total numbers reaching the age of first capture equal to the ratio of fishing mortality to total mortality.
In the same way the weight caught in the time interval t, t + dt, is given by
dYt =FNtWtdt
where Wt is the average weight of a fish of age t.
The total weight caught will therefore be given by
..................... (9.3)
For this to be easily integrated, the expression for the weight has to be in a suitable form; of the growth equations discussed earlier, that of von Bertalanffy is one of the most convenient. That is, we can write
Or, writing the right hand side as a summation,
where
U0= 1, U1 = - 3, U2= 3, U3 = - 1
Then
or, writing t - t0 = (t- tc) - (tc - t0) and rearranging the terms
on integrating this becomes
... (9.4)
Again this expression may be simplified if tL is sufficiently large for the last term to be neglected. The yield is given by
or, substituting for R'
.... (9.5)
Besides the total yield, some other quantities are important. Thus the yield is F times the average biomass of fish in the exploited phase, B', and therefore
.............(9.6)
Similarly, the average number in the exploited phase is, from equation (9.2'), dividing the catch in numbers by F
The average weight of the individual fish in the exploited phase is therefore
Because the recruitment is unknown and often variable, the yields etc. are normally calculated as yield etc. per recruit.
The steps in calculating the yield directly from equation (9.5) have been set out in the attached work sheets. The first, A, shows a layout for calculating yield for a range of values of fishing mortality, F, selectivity (tc) being constant. The entries in the box at the top left will be completed from the knowledge of the various parameters in the stock, either using the best estimates available, or, if the knowledge is not so precise, a range of values for natural mortality etc.; a separate sheet is used for each set of possible values. The entries in the top middle deal with the calculations which are the same for all values of F. Below are four pairs of columns, (B) and (C), corresponding to the four terms in the summation of equation (9.5). (For convenience most of the entries, columns etc. have been labelled with letters; when referred to in later column headings they are enclosed in brackets, to avoid confusion with the letters used for mortality coefficients etc. In the second row of each column is shown the formula which will normally be used in computing the entry in that column, the third row shows what the entry represents in terms of the various parameters.)
The other work sheets, B.1 and B.2, are used for calculating the yield for varying selectivities. The first is used to calculate tc and related quantities from the selectivity, which will normally be defined by the size at first capture lc. The yield for the range of selectivities and any particular fishing mortality can then be calculated as on sheet B.2, which is nearly the same as work sheet A.
It is possible to reduce the calculations and also to take into account a length-weight relationship other than the cubic, by expressing the yield Y in another form using the incomplete Beta function.
This function, which is usually denoted by Bx (p, q) is defined by the integral
where p, q are positive constants and the upper limit of integration, x, is between 0 and 1. For x = 1 the expression is the complete Beta function B (p, q).
To obtain the yield in terms of the Beta function we have, from equation (9.3), for tL = ¥
where
which noting that t - tc = (t- t0) - (t0 - tc) can be written as
or if W¥ is proportional to lb
Using the transformation
and calculating the limits of integration, for the new variable,
t = ¥ becomes y = 0
Also the expression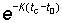 
, which is equal to 
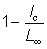will be denoted by 1 - c. The different factors in the integral then become
The yield in weight, Y, then becomes
or writing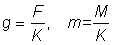 
Expressing the integral as an incomplete Beta function this becomes
or if b = 3
...... (9.7)
That expression for the yield can be considered in two parts; the first (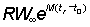
) does not contain either of the parameters (F or tc) which depend on the amount or pattern of fishing. This part can therefore be considered as constant in studying the effect on the yield of different patterns of fishing. The second part contains only four parameters, the ratios m = M/K, g = F/K and b and c.
Tables of the incomplete Beta function are available (Jones, 1957; Wilimovsky and Wicklung, 1963). Tables of g (1 - c)g have been given by Holt (1957). Thus the yield can be expressed as the product of a constant and two quantities obtainable from the tables.
It should be noted that
i.e. it is the proportion of the total growth in length which is made up before the fish enters the exploited phase. Despite the apparent complexity of the expression for the yield, it is determined by only a few quantities: the proportion of the growth completed when the fish is recruited, and the relative magnitudes of the fishing mortality, the natural mortality, and the growth parameter K.
Since b in fact rarely departs appreciably from 3, equation (9.7) can normally be used. Apart from a constant term, at the beginning, this has only three independent variables, C, g, and m and a function of three variables can be readily tabulated directly. This has been done by Beverton and Holt (1964) explicitly as a function of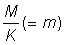 
, c and 
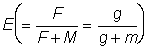. (Examples of these tables are given in Appendix 1.) They deduced the formula in a slightly different form, but it is a matter of simple mathematics to express their expression (12) for 
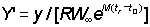in terms of c, m and g, i.e.
which may be shown to be equal to g (1 - c)-g B1-c (m + g, 4).
These yield tables have been tabulated for a series of values of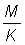 
from 0.25 to 5.00. For each value of 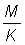, the table of values of Y' (proportional to the yield per recruit) forms the equivalent of a yield isopleth diagram from which the form of the relationship of yield with amount of fishing or size at first capture can be determined very easily. Some care should be taken in interpreting changes on the amount of fishing, since the tabulations are given in terms of 
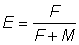and for large values of E - over 0.5 - quite small changes in E correspond to large changes in F.
Other forms for the yield can be obtained by substituting different formulae for the weight in equation (9.3). In particular, over any moderately short period of time, say to, growth in weight may be treated as exponential;
where w1 is the weight at time t1.
The growth coefficient g1 will change according to the interval chosen, generally decreasing with increasing age. Substituting, the yield in weight during the period t1 - t2 is
The total yield may then be obtained by summing over the whole life span, using a sufficient number of intervals. By expressing growth in this form, it may be seen that the size (or age) at which the total mass of a year-class is at its maximum is the size at which g is equal to the natural mortality coefficient M (the "critical size" of Ricker). The greatest yield is then obtained by taking all the year-classes as soon as they reach this size. Where the assumptions of the simple yield equation are not fulfilled (e.g. different growth pattern, parameters not constant, etc.), there is always the possibility to apply the method mentioned in the second paragraph of this section of expressing the yield as the sum of the yields in a large number of small time intervals, within which changes in the size of the individuals and the number of individuals in the stock can be ignored. That is, we approximate to the integral of equation (9.3) by the expression
where the time interval tc to tL. has been divided into k short intervals, and
Fi = fishing mortality in the ith period
Ni = numbers present at the beginning of the ith period
Wi = average weight of individuals during the ith period
and D ti = duration of the ith period.
Fi may be taken as constant = F, or some empirical values can be used if there is evidence that fishing mortality varies with age. Similarly, Wi can be determined from a suitable growth curve, or again empirical data can be used to take into account factors such as seasonal variations on growth, etc.
Ni can be determined from the usual formula
or from the equations
N1=R'Ni+1 = Ni - (Fi + M) NiD ti
The expression of the yield in this form is likely to be particularly useful in any fishery where the assumptions of the simple yield curve are not very closely fulfilled; for instance, very seasonal fisheries, or fisheries such as those with gill-nets, where the fishing mortality may vary with age. Detailed computer studies have been made for the Pacific salmon fisheries where there are complex regulations involving several gears, and a large number of stocks mixing to a greater or lesser extent.
A. EFFECTS OF CHANGE IN FISHING INTENSITY
A.1 North sea plaice (75-mm mesh)
Approximate parameter values for North sea plaice, with a 75-mm mesh, are as follows:
M = 0.1
L¥ = 68.5 cm
W¥ == 2 860 g
K = 0.095
t0 = - 0.8 year
tr = 3.7 years
tc = 3.7 years
(Note that North sea plaice do not move into the main fishing grounds until they are three to four years old so that the size at first capture is independent of mesh size for meshes up to about 100 mm.)
1. Using work sheet A, calculate and plot against fishing mortality coefficient (F), curves of exploited population weight per recruit (B'/R) (proportional to catch per unit effort).
Yield per recruit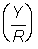 
. Express this in grammes, and also as a percentage of the present yield (i.e. with F == 0.5).
Exploited population numbers per recruit 
.
Catch in numbers per recruit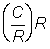 
.
Average weight of fish in catch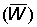 
.
(Note: Take F=0, 0.02, 0.04, 0.06, 0.08, 0.1, 0.2, 0.5, 1.0.)
2. From the tables of yield functions (Appendix 1) using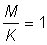 
, express the yield per recruit for each value of E in the tables as a percentage of the yield per recruit at the present value of E (take this as 0.8). Plot this value (a) against E, and (b) against 
.
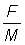(Note: First calculate c.) How does curve 2 (b) compare with the curve of yield per recruit against effort obtained in 1?
3. Repeat 2 for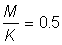 
and 1.5.
4. The present estimate of F for North sea plaice is about 0.5. What percentage change in fishing intensity from the present level is needed to obtain the greatest steady yield per recruit? By what percentage does this yield diner from the present level? What effect would this change in intensity have on the catch per unit effort and the mean weight of fish in the catch? How do these answers depend on the magnitude of M?
5. Repeat for 140-mm mesh, given that tc for this mesh size is 5.5 years.
A. 2. North sea haddock (75-mm mesh)
Approximate parameter values for North sea haddock with a 75-mm mesh are as follows:
M = 0.2
L¥ = 55 cm
W¥ = 1 300 g
K = 0.25
t0 = -0.2 year
tr = 1.0 year
tc = 2.1 years
1. Carry through the exercises A.1, and 2, as detailed above. Note: The present estimate of F for North sea haddock is about 0.8; in the yield tables use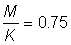 
.
2. Repeat with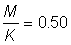 
and 1.25.
3. Repeat for 100-mm mesh, given that tc = 3.3 years.
B. EFFECTS OF CHANGE IN MESH SIZE
B.1. North sea plaice (F=0.5)
1. For mesh sizes above 120 mm, the mean selection length lc can be calculated directly from the selection factor (b) = 2.2. Using work sheets B.1 and B.2, with F = 0.5, calculate and plot against mesh size curves of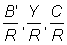 
and 
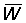. Take M = 0.1 and other parameter values as listed in A.1. Express the yield as a percentage of the present yield; i.e. with a mesh of 75 mm. (Note: Take mesh sizes of 120, 160, 180, 200, 220, 240 and 260 mm, and also plot the values for meshes of 75 mm and 140 mm previously calculated for F = 0.5.)
2. Use the yield tables for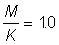 
to determine the form of the curve of yield per recruit against mesh size. Repeat for 
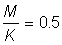, (first calculate E and use nearest value of E in tables).
3. What mesh size is needed to give the greatest steady yield per recruit with this value of F? By what percentage does this yield differ from the present level? What would be the corresponding changes in catch per unit effort and average weight of fish in the catch? How do these answers depend on the magnitude of M?
4. Work through examples 1-3 as in B.1 above, but using F = 0.2 throughout. Compare your results and conclusions with those for F = 0.5.
B.2. North sea haddock (F = 0.8)
1. The relation between mean selection length lc and mesh size in haddock can be calculated with a selection factor of 3.2. Using work sheets B.1 and B.2, with F = 0.8 throughout, calculate and plot against mesh size curves of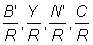 
and 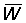. Take parameter values as listed in A.2. (Note: Take mesh sizes of 80, 90, 120, 140, 150, 160. Plot also values previously calculated for meshes of 75 and 100 mm with F = 0.8.)
2. Use the yield tables to determine the form of the curve of yield per recruit against mesh size for 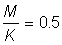, 0.75 and 1.25 (use E = 0.85, 0.80, 0.70).
3. What mesh size is needed to give the greatest steady yield per recruit with this value of F? By what percentage does this yield differ from the present level? What would be the corresponding changes in catch per unit effort and average weight of fish in the catch? How do these answers depend on the value of M?
4. Work through examples 1-4 as in B.2 above, but using F = 0.3 throughout. Compare your results and conclusions with those for F= 0.8 and also with those for the North sea plaice.
WORK SHEET A. - Fishing intensity assessments
WORK SHEET B.1. - Mesh size assessments (1)
WORK SHEET B.2. - Mesh size assessments (2)
