10.1 Catch and effort statistics
10.2 Schaefer's model
10.3 Changes in selectivity
10.4 Interacting fisheries
10.5 Exercises
The simple yield equation described in the earlier sections depends for its calculation on fairly complete knowledge of the various parameters (growth, mortality, etc.), and with this information it is possible to estimate the steady yield for any combination of fishing mortality and age at first capture. However, even if, as very often happens, information is far from complete, it is possible to answer certain specific questions, e.g. would a moderate increase in size of first capture increase or decrease the steady yield?
If statistics are available for a number of periods in which the effort was kept at a steady level it would clearly be possible to derive a purely empirical relation between fishing effort and steady yield, or catch per unit effort. In most fisheries there are few, if any, long periods of constant fishing effort, and the catch and catch per unit effort in any one year will be related not only to the effort in that year, but to the effort in several preceding years. However, the abundance of a particular year-class which has been in the fishery for say four years (i.e. is of age tc + 4), will be governed by a factor equal to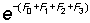 
where F0, F1, F2, F3 are the fishing mortalities in the previous four years; i.e. its abundance will be the same as if it had been in a fishery with a steady fishing mortality of 
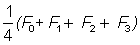. The total catch per unit effort (cpe) of all ages is then related to some weighted mean of the fishing effort in the previous years. If this mean is taken over a period equal to the mean duration of life in the exploited phase (e.g. if the age at recruitment is four years old, and the major part of the catch, in weight, is made up of fish between four and nine years old, the mean duration is about three years), then the relation between this mean effort, 
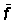, and cpe will be close to that between effort and cpe in the steady state. The agreement will in fact be almost exact, not only when the effort has not altered greatly, but also when there has been a steady trend in effort. For instance if effort has been increasing, then the older ages will be over-abundant, having had an average fishing effort on them less than 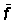, while the younger ages will be too scarce, having experienced an average effort greater than .
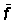This relation is best expressed graphically by plotting cpe against/; the best fit is usually not a straight line, but a curve concave upward, for instance the curves for plaice or cod at Iceland (Gulland, 1961b). From this curve, giving the steady state relation between cpe and effort, the corresponding relation between catch and effort can be determined at once by multiplication.
This approach is very close to the constant parameter model of the complete yield curve, in which density-dependent effects are ignored, as most of these take effect over longer periods of time. For instance, in the example above, if recruitment is affected, the present stock is the offspring of the stock on the average six to seven years earlier, which in turn was determined by the fishing over the previous three years or more.
The major advantage of this method is that it requires easily obtainable data; total catch is usually known, and effort or cpe data are usually among the earliest semiscientific data to be collected. If there are errors in the effort data (the most likely being uncorrected trends, such as increased efficiency) these will affect both x and y values in the plotting, and tend to displace the points along lines of the form y = a/x. The displacement is in a similar direction as the general form of the expected regression, so that it appears that errors in effort measurement will not distort the estimate of the relation between cpe and effort, but may make the statistical significance of the fit greater than it really is. If the series of data is long enough the effect of changes other than simply of total effort may be studied. Thus if there has been a change in fishing practice, e.g. an increase of mesh size, in the middle of the series, then, if this has had a significant effect on the stock, two different regressions of cpe on effort for the periods before and after the change could be determined.
Another method of analysis depending chiefly on catch and effort data is that of Schaefer, 1954, 1957. The population biomass, B, is considered as a single entity, which would, if fishing were not present, increase at a rate determined by its size, i.e.
where f (B) is some function of B, being zero when B = 0, and when B is at its maximum BM, and f (B) will have a maximum at some intermediate value of B.
Therefore, when fishing is present
Clearly the population will remain constant if Y = f (B), so that at any population size there will be a certain equilibrium catch, and this will be a maximum when f (B) is a maximum.
The form of f (B) may be determined from data on catch and effort, provided there is also some information (e.g. on tagging) from which catch per unit effort figures can be converted into absolute terms, i.e. if the coefficient q (k2 in Schaefer's notation) is known. Thus if the values of catch per unit effort are known at the beginning and end of a year
then B2 - B1 = change in population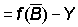 
or 
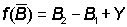where Y is the catch during the year.
Usually the catch per unit effort will not be known at the beginning of the year, but as the mean value over the year. The catch per unit effort at the beginning of the year may instead be estimated as the mean of the average catches per unit effort during the preceding and subsequent 12 months. A pair of values of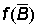 
and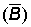 
can therefore be obtained for each year, and by plotting one against the other the relation between equilibrium catch and stock size may be established. The fitting may be made more quickly if some form for f (B) is assumed, for instance the relation
f (B)=aB (BM - B)
which plotted against B gives a parabola. This form of curve is best fitted by plotting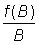 
against B, which gives a straight line. This method of analysis has much in common with that of the previous section. Both attempt to obtain the equilibrium relation between catch and effort (or one of its transformations) by suitable adjustment of data from a changing fishery - one by taking into account effort data in earlier years, and the other, changes in the catch per unit effort. This model has apparent advantages of simplicity and only a small demand on data. Also it gives the impression of being more closely related to the realities of natural population than the analytic model of the earlier section, at least when for the latter no account is taken of possible changes in the parameters of growth, mortality and recruitment, related to changes in the abundance of the population.
These advantages are, however, mainly superficial. The analytic model can be modified to take into account the complexities of any natural population whereas the Schaefer model is very difficult to modify. Also the natural rate of increase of a population is not determined uniquely and solely by the population biomass at one time. The recruitment is determined (apart from environmental factors) by the adult stock some time in the past, often several years. The increase in population biomass due to growth either absolutely or as a percentage of the present biomass depends as much if not more on the age structure of the population than on its total biomass. To take these effects into account the use of some form of analytic model is required.
The simplest and perhaps the most important question concerning the effect of a possible change in selectivity is whether the change will result in an increase or decrease in the average catch. This can be done, following Alien (1953), by comparing the weight of the individual fish of the size it is proposed to release, with the probability of their being caught again later and their average weight when caught. That is, if
Wc = weight of individual fish at the mean selection length= mean weight of fish in the catch larger than Wc
then the catch will be increased by releasing the fish if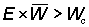 
where E = probability of a released fish being caught later 
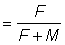if the fishing and natural mortalities are constant. Or, in terms of the We ratio of fishing to total mortality, the catch will be increased if 
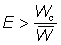. The right-hand side of this inequality can be readily calculated from simple observations of the size composition of the catches.
Some more detailed effects of changes in selectivity can be also determined from a knowledge of the size composition of the landings (see Gulland, 1961a, 1964a). Thus, immediately following a change in gear there will be no change in the stock, and the numbers of any given size, l, of fish landed by the new gear (e.g. increased mesh size) will be given by
.................... (10.1)
where
iN1 = numbers landed by old gear
lNk = numbers landed by new gear
lr1 = proportion retained by old gear
lr3 = proportion retained by new gear.
If also lW = average weight of fish of length l then the total weight W1, caught with the old gear, is given by
W1 = S lWlNi ................... (10.2)
and weight caught with the new gear, Wk, is
Wk = S lWlNk ................... (10.3)
Also the total numbers landed by the old gear, N1, and retained by the new gear, Nk, can be written
N1 = S l N1, and Nk = S l Nk.
(If the average weights lW and the relevant numbers are arranged as parallel columns these calculations of sums of products are simple to carry out on most calculating machines.) The actual immediate change in landings can be expressed as a proportion L of the initial landings, where
When an increase in mean selection length takes place the fish released by the new gear, but which could have been caught by the old gear, will grow, and after a time reach the size at which they will be retained by the new gear, and the catches will increase.
The number, NR, of fish released, which would previously have been landed, will be equal to N1 - Nk. If quantities of small fish are caught and discarded at sea, and not landed, the total numbers released will be greater than the reduction in the landings, and may be calculated as
.................(10.4)
where lNc are the numbers of fish of length l caught by the old gear including discards. Of these fish a number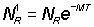 
will survive to 2tc, the mean age of first capture with the new mesh, where T is the difference between 2tc and the average age of the fish released. In turn, of these fish a number 
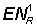will ultimately be caught, where E is the exploitation rate (
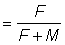when the mortalities are constant). As all the mortalities etc. for fish greater than 2lc are unchanged, the size distribution of these fish will be the same as that of the Nk fish, so that after a period the catches with the new gear will be increased by a proportion Q, when
..................... (10.5)
Thus the long-term landings, W2, will be given by
W2 = W1 (1 - L)(1 + Q) ................ (10.6)
This level of landings may not be reached until several years after the change in selectivity. It will only be complete after a period, equal to the life span of the fish in the fishery, has elapsed since the change in selectivity, although it will be close to this value at a rather earlier date. The catches in the interim period can be estimated as follows. In order to estimate the landings at time t', suppose that fish of the size released will have grown to a certain length l'. Then, at a time t' after the change in mesh size, the fish larger than l' will have been fished by the old mesh when they were of a size in the selection range, so that the stock and catches of these fish will be nearly unaffected by the change, and the weight caught of fish length l > l' would be lWlNR. Fish smaller than length l' would have been under the influence of the new mesh during their life in the exploited phase so the stock and catches of these sizes could be the same as in the long-term equilibrium state with the new mesh, and the weight caught of fish length l < l' would be (1 + Q) lWlNR. The total weight caught will be W', given by
i.e.
..................... (10.7)
The method can be extended to stocks fished with more than one gear, some of which may not change their selectivities. Here equations (10.1) and (10.3) are applied separately to each fleet to find the immediate effects. The factor Q will be the same for all, and is given from the extension of equation (10.5) in the form
..................... (10.8)
where the summation of Nk includes the fish caught by all gears (omitting any fish, caught by gears whose selectivity does not change, smaller than the new selection length), but the summation of NR will, of course, only include gears whose selectivity changes. The calculations necessary to assess the results of a mesh change when two gears, possibly catching different sizes of fish, are operating are set out in the work sheet on p. 127.
The above methods may also be used to study the interaction of different fisheries, particularly of a fishery (A) principally for one species (e.g. herring) which incidentally catches young fish of another species (e.g. haddock), which, when older, is itself the principal object of some other fishery (B).
The steps are again
(a) Calculate the number of fish caught by fleet (A), or the extra number being caught compared with what would have been caught supposing fleet (A) was complying with some desired regulation (= N).
(b) Calculate the reduced numbers of these which will survive until the age of first capture of fleet (B) (= N1).
(c) Compare the numbers of these = EN1, which would be caught, with the present catch, C, of fleet (B). Then the increase in the catches of fleet (B) which would take place if fleet (A) stopped fishing, is, as a proportion of the present catch: EN1/C. The same result may be obtained by comparing N1 with the numbers of fish recruiting to fleet (B), which is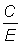 
(see International Council for the Exploration of the Sea, 1960).
WORK SHEET C. - Assessment of changes in selectivity (for two gears with different size compositions of their catches)
1. The table below gives the catch per unit effort (catch, in tons, per 1 000 ton-hours' fishing by United Kingdom trawlers) and the total catch, in thousands of tons, of cod and haddock, at Iceland.
(a) Calculate the total fishing effort, in United Kingdom units, on cod and on haddock each year.
(b) If the average duration of life in the fishery is two years for haddock and three for cod, relate the stock abundance to the past fishing effort. Is there any suggestion that either of these relations has changed? In particular, examine the haddock curve for the years since 1950, when a larger mesh was introduced and trawling was banned in certain areas, including some nursery areas.
2. The table below gives data on catches and catch per unit effort of blue whales in the Antarctic. Taking alternative values of the population size corresponding to a catch per unit effort of 1.00 as 20 000 and 30 000 whales, calculate the change in population size each year, and hence the sustainable yield each year. Plot this against population size in that year, and that five years earlier (assuming blue whales recruit to the exploited stock at five years of age). How may the catch data for the years 1939-46 be used? What is the maximum sustainable yield, and at what population size is it taken?
|
Year |
Total catch |
Catch per unit effort |
|
1925/26 |
4 697 |
3.30 |
|
1926/27 |
6 545 |
3.76 |
|
1927/28 |
8 334 |
4.39 |
|
1928/29 |
12734 |
4.49 |
|
1929/30 |
17 898 |
3.13 |
|
1930/31 |
29 410 |
3.71 |
|
1931/32 |
6488 |
4.83 |
|
1932/33 |
18 890 |
4.61 |
|
1933/34 |
17 349 |
4.76 |
|
1934/35 |
16 500 |
3.46 |
|
1935/36 |
17731 |
3.96 |
|
1936/37 |
14304 |
2.83 |
|
1937/38 |
14923 |
2.00 |
|
1938/39 |
14081 |
1.77 |
|
1939/40 |
11 480 |
|
|
1940/41 |
4943 |
|
|
1941/42 |
59 |
|
|
1942/43 |
125 |
|
|
1943/44 |
339 |
|
|
1944/45 |
1 042 |
|
|
1945/46 |
3 606 |
1.36 |
|
1946/47 |
9 192 |
1.85 |
|
1947/48 |
6 908 |
1.12 |
|
1948/49 |
7 625 |
0.98 |
|
1949/50 |
6 182 |
0.80 |
|
1950/51 |
7 048 |
0.81 |
|
1951/52 |
5 130 |
0.63 |
|
1952/53 |
3 870 |
0.44 |
|
1953/54 |
2 697 |
0.42 |
|
1954/55 |
2 176 |
0.31 |
|
1955/56 |
1 614 |
0.37 |
|
1956/57 |
1 512 |
0.27 |
|
1957/58 |
1 690 |
0.28 |
|
1958/59 |
1 187 |
0.18 |
|
1959/60 |
1 228 |
0.14 |
|
1960/61 |
5871 |
0.105 |
|
1961/62 |
6391 |
0.093 |
1 Omitting pygmy blue whales
3. Data for the United Kingdom trawl fishery for haddock at the Faroe islands are given below, showing the numbers landed in each 5-cm-length group, their average weight, and the proportion of each group retained by a 90-mm and a 120-mm mesh.
|
Length |
Average weight |
Percentage retained |
Numbers landed | |
|
cm |
8 |
90 mm |
120 mm |
Thousand |
|
25-29 |
160 |
50 |
3 |
8 |
|
30-34 |
260 |
80 |
16 |
314 |
|
35-39 |
420 |
98 |
41 |
1 084 |
|
40-44 |
630 |
100 |
72 |
1 409 |
|
45-49 |
880 |
100 |
94 |
1 370 |
|
50-54 |
1 190 |
100 |
100 |
952 |
|
55-59 |
1 570 |
100 |
100 |
465 |
|
60-64 |
1 760 |
100 |
100 |
255 |
|
65-69 |
2 530 |
100 |
100 |
124 |
|
70-74 |
3 100 |
100 |
100 |
73 |
|
75-79 |
3 800 |
100 |
100 |
30 |
|
80+ |
4 600 |
100 |
100 |
9 |
(a) What is the present total weight landed?
(b) If the present mesh was 90 mm, what would be the reduction in catch (as a percentage) immediately following an increase to 120 mm?
(c) If it takes an average of six months for the fish released to grow to the size of first capture of the 120-mm mesh, what would be the long-term effect of an increase of mesh to mm, assuming that there is no other fishery, and that the natural mortality of fish in the selection size is 0.2, and E (= F/F + M) = 0.5?
(d) What would be the long-term effects on both fleets (as percentages, and actual weights) if there was also a line fishery operating, taking an average annual catch of five million fish weighing 6 000 tons, and E =0.77 Assume all line-caught fish are larger than the selection size of the 120-mm mesh.
(e) What would be the effects if the trawlers discarded 30 percent of the catch (by numbers), and these fish were all small enough to escape through a 120-mm mesh? (Let T == one year, say.)
4. The average annual catch of haddock by trawlers fishing for herring in 1954-56 was as follows:
|
Size |
Weight caught |
Weight landed |
Fish |
|
Tons |
Million |
||
|
Under 24 cm |
2 500 |
- |
25 |
|
24-27 cm |
6 000 |
- |
45 |
|
Over 27 cm |
23 500 |
14 000 |
80 |
|
Total |
32000 |
14 000 |
150 |
The fishery for haddock lands on an average 70 000 tons per year of fish whose average weight is 330 g.
If the herring trawlers were to use a mesh of the minimum size for demersal fishing, what would be the effect on the haddock catches assuming:
(a) The legal mesh releases all haddock less than 24 cm.
(b) In the haddock fishery some 100 million fish over 24 cm are caught, but are rejected as being below the marketable size of 27 cm.
(c) The fish below 24 cm which would be released by a larger mesh take an average of six months to grow to 24 cm, during which time they would suffer a natural mortality of 0.2.
(d) E = F/ (F+ M) =0.8 (where F includes all forms of fishing).
