KLAUS STERN
La genética de poblaciones ofrece buenas oportunidades para planificar nuevos programas de mejora o perfeccionar los ya existentes. Este capitulo tratará de los aspectos principales y de los métodos de que dispone el mejorados forestal, así como de algunas dificultades que ano encuentra el qenetista de poblaciones que precisan ser superadas.
La primera sección describe un modelo matemático para poblaciones arbóreas naturales o indígenas. Dicho modelo parte de que la población arbórea dentro de una región dada, de condiciones ecológicas relativamente homogéneas, puede estar dividida en subpoblaciones, cada una de las cuales ha de considerarse derivada de una población que se aparea libremente y al azar. Este modelo debe ser adaptado a cada situación particular para que responda a la realidad. Se espera que los resultados que se obtengan signifiquen una ayuda positiva.
Por el empleo de este modelo matemático, se pueden calcular ciertas cantidades o parámetros genéticos y de ello se trata en la segunda sección del capitulo. Dichos parámetros son:
1. heredabilidad (h²), que se define como la fracción de la variación total debida a causas genéticas;2. correlación genética, que es una medida del grado de enlace genético entre dos o más caracteres en el mismo individuo;
3. el coeficiente de consanguinidad (F), que expresa la desviación de un sistema concreto de apareamiento del de una población de apareamiento al azar.
En la tercera sección de este capitulo se presentan algunas ideas sobre diseños de apareamiento, ensayos de campo, efectos de la competición sobre la selección y efectos de las interacciones entre genotipos y ambientes sobre la estimación de la heredabilidad. Se muestra que los diseños de apareamiento basados en cruzamientos dialelos dan la máxima información (el tipo básico del cruzamiento dialelo está constituído por la serie de todos los cruces posibles en el grupo de árboles sometidos a prueba).
En relación con las pruebas de campo se señala que la elección del diseño, tamaño de las parcelas y demás particularidades, deben variar con la clase de experimento si se persigue la máxima eficacia. En el momento presente, sin embargo, se tienen escasos conocimientos sobre muchos problemas relacionados con las pruebas de descendencia.
La forma de acelerar el progreso en los programas de mejora y de sacar la máxima utilidad del material mejorado se tratan en la última sección de este capitulo.
La conclusión principal es que el mejorador de especies forestales debe intentar por el momento la obtención de resultados prácticos y de estimaciones de los parámetros genéticos en los mismos experimentos. A causa de la falta de información aún no es posible indicar los más convenientes procedimientos de mejora. Por el empleo de la genética de poblaciones pueden encontrarse métodos de relativa eficacia.
Factores de evolución y sus efectos en las poblaciones de árboles forestales
KLAUS STERN es jefe de investigación en el Institut für Forstgenetik und Forstpflanzenzüchtung, Schmelenbeck, de la República Federal de Alemania. Otros miembros del equipo de trabajo fueron A. de Philippis (Italia) y G. Sirén (FAO), L. Strand (Noruega), H. Johnsson (Suecia) y R. Toda (Japón).
Durante las últimas décadas ha habido un progreso notable en la genética de poblaciones y en la genética de caracteres cuantitativos. Sus resultados y métodos han sido ampliamente utilizados en genética forestal. Este capítulo explica como hay que aplicarlos a la mejora selectiva de los árboles forestales.
El problema en cuestión puede plantearse de la siguiente forma. Considérese una especie arbórea importante económicamente, con un área geográfica determinada; se conoce que existen diferencias genéticas entre medias de subpoblaciones de esta especie y entre árboles pertenecientes a una misma subpoblación. A través de la mejora selectiva se desea emplear para la práctica forestal:
1. la variabilidad genética entre las subpoblaciones;2. la variabilidad genética entre individuos de la misma subpoblación arbórea.
El primero de ambos problemas será explicado de forma más completa en la tercera sección de este capítulo. Al discutir el segundo se debe, sin embargo, incluir también la variación entre subpoblaciones, ya que los árboles con los que trabaja el mejorador son seleccionados corrientemente en subpoblaciones diferentes.
La diferenciación genética entre subpoblaciones se deriva de acontecimientos evolutivos que conducen hacia el desarrollo de las especies y cuya influencia sobre las mismas continúa. Aquí solamente presentan interés cuatro complejos de factores evolutivos:
a) accidentes de muestreo;
b) selección natural;
c) migración;.
d) introgresión.
La introgresión no se considerará en detalle, aunque hay casos en que no debe ser olvidada. Quedan aún algunos otros factores de evolución de los que no se tratará aquí. (Consúltese especialmente S. Wright, 1955 y Stebbins, 1950, para una revisión completa de los factores evolutivos.)
La selección natural y los accidentes de muestreo provocan diversificación genética entre las subpoblaciones, pero la migración actúa en sentido contrario. Los tres obran, sin embargo, simultáneamente, de forma que el genetista forestal se enfrenta con una estructura poblacional que debe ser considerada como una fase de un proceso en el espacio y en el tiempo. Normalmente los tres factores se compensarán y esta compensación no ha de estar muy lejos de un estado de equilibrio que permita diferencias genéticas entre subpoblaciones motivadas por la selección natural y los accidentes de muestreo.
Por esto el genetista forestal rara vez, si es que existe alguna, trata con poblaciones de apareamiento libre y al azar. Por el contrario, la distribución de genes mostrará desviaciones considerables del equilibrio de Hardy-Weinberg. Esto vale también para especies forzosamente alógamas.
Modelo general de estructura poblacional para la mayoría de las especies arbóreas
La variación entre subpoblaciones que cubren toda el área de la especie, o una gran parte de la misma puede ser dividida en dos partes:
1. un componente de variación entre regiones geográficas;
2. otro componente resultante de diferencias genéticas entre subpoblaciones dentro de la misma región.
El primer componente reflejará en gran medida los efectos de la selección natural, mientras el segundo puede ser causado por selección natural o por accidentes de muestreo, o por ambos factores.
En la mayoría de los casos el componente «interregional» puede ser separado además por medio de técnicas de regresión (variación clinal, como demostró Langlet, 1936 y trabajos posteriores). La variancia restante tiene por consiguiente la misma interpretación dada al componente «intrarregional».
Se admite aquí que los accidentes de muestreo constituyen la fuente principal de la variancia intrarregional. Si la selección natural fuese también una fuente de varianza intrarregional, tendríamos que presumir una distribución aleatoria de ambientes, para tratar esta variación en forma similar a los accidentes de muestreo.
Adoptando estas suposiciones se puede admitir que: dentro de una región dada se pueden concebir las subpoblaciones como un grupo aleatorio de líneas consanguíneas derivadas de la misma población de apareamiento al azar o población base.
Los mejoradores de árboles trabajarán siempre para ciertas regiones (tales como el Wuchsgebiet de Alemania y plantagezonen de Suecia). Este modelo de población natural de una especie arbórea dentro de los límites de una región, da al mejorador una oportunidad de trabajar con una población definida, cosa necesaria si quiere utilizar métodos de genética cuantitativa. Los límites de la «región» en el sentido de la definición dada anteriormente se eligen considerando condiciones climáticas y los resultados de investigaciones biosistemáticas (Callahan, 1963). En caso necesario es posible corregir los límites por el resultado de los ensayos de procedencia.
Según la definición, la población dentro de la «región»no tiene una estructura de apareamiento al azar. Está subdividida en varias subpoblaciones que difieren más o menos de la media general. Admitiendo que las subpoblaciones se han derivado aleatoriamente de una población base común y que tienen igual consanguinidad, podemos estar en posición de superar esta dificultad como se indicará más adelante en este capítulo.
Estructuras de población excepcionales en árboles forestales
El modelo de población del párrafo anterior no es aplicable si:
1. la forma usual de propagarse la especie es vegetativamente, como sucede con los sauces y chopos;2. la especie es autofecundante, como es lo más probable que ocurra con las especies de los bosques tropicales lluviosos (Baker, 1959);
3. la estructura natural de las poblaciones ha sido ampliamente destruida debido a la repoblación artificial.
En los tres casos es necesario determinar experimentalmente las condiciones presentes.
Concepto de heredabilidad
Considérese ahora un carácter cuantitativo que muestre variación continua. Su manifestación en un cierto individuo o en una familia está determinada por el «valor genotípico»del individuo o de la media familiar, y por la «desviación ambiental» por la cual y debido a diferencias de ambiente, el comportamiento del individuo o de la familia difiere del comportamiento medio de la población entera. Podemos considerar el comportamiento fenotípico como una combinación lineal del valor genotípico y de la desviación ambiental:
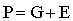
Si G y E no están correlacionadas, la variancia de los valores fenotípicos es también una combinación lineal de sus variancias:
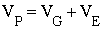
Al cociente
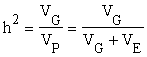
se le llama «heredabilidad» del carácter en esa particular población. Las heredabilidades pueden ser interpretadas como las regresiones de los valores genotípicos sobre los fenotípicos y ésta es la razón del extenso uso de las heredabilidades al trazar los programas de mejora.
Existen varias clases de heredabilidad. Si (VG) representa la variancia genética total en una población, entonces el cociente da la heredabilidad «en sentido lato». Si la variancia genética total (VG) es reemplazada por la variancia resultante de los efectos génicos aditivos (VA) el cociente dará la heredabilidad «en sentido estricto» (Lush, 1937 y trabajos posteriores). En ambos casos, el denominador es la variancia fenotípica total, que es la suma de la variancia genética total (resultante de la variancia aditiva, la dominancia y la epistasis de los genes) y la variancia ambiental.
En la selección masal y procedimientos de mejora con ella relacionados solamente puede utilizarse la variancia genética aditiva. Entonces tiene que ser empleada la heredabilidad en sentido estricto. Cuando es posible la propagación vegetativa de clones selectos para uso práctico inmediato, puede emplearse la heredabilidad en sentido lato.
La heredabilidad puede emplearse para la solución de diferentes problemas:
1. la heredabilidad que representa la fracción genética de la variación fenotípica entre individuos dentro de una población;2. la heredabilidad que representa la fracción genética de la variación fenotípica entre familias, procedencias, etc., en una experiencia particular de campo.
En el primer caso, h² es un parámetro de una población; en el segundo, es un parámetro de una experiencia particular.
Hanson (1961) define como heredabilidades las expresiones matemáticas que miden el progreso esperado de la selección. Su argumento principal es que el mejorador sólo considera la heredabilidad por esa razón. Mergen (1960) utiliza la heredabilidad como una medida de «la rigidez del control genético» de caracteres cuantitativos. Esta es otra aplicación indicando que la heredabilidad está siempre relacionada con un experimento o población específica: ha puede ser utilizada como una medida de la eficiencia de una experiencia (R. L. Anderson, 1960). Hattemer (1963) da una lista de las heredabilidades publicadas hasta 1963 y presta atención también a varios problemas relacionados con la estimación de la heredabilidad en especies forestales.
Aptitud combinatoria
El concepto de aptitud combinatoria ha sido definido por Sprague y Tatum (1942) para líneas consanguíneas de maíz. Sin embargo es posible aplicarlo también a otro material. La aptitud combinatoria no es un atributo de un individuo o línea, sino un atributo del individuo o línea y la población de otros individuos o líneas sometidos a investigación. Sprague y Tatum definieron la aptitud combinatoria por medio de un análisis de variancia bifactorial que puede ser adaptado a una serie de cruzamientos dialelos. La producción yij de la descendencia de cruzar el individuo o línea i-ésimo con el i-ésimo se compone de los efectos medios (ai y aj) de ambas líneas sobre todas sus combinaciones con los otros individuos o líneas del experimento, y una desviación específica representada por sij; siendo m la media total:
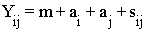
La variancia resultante de las ai y aj es entonces la variancia de la «aptitud combinatoria general»; siendo la variancia de sij; la de la «aptitud combinatoria específica».
Si los genitores son una muestra extraída de una población que se aparea al azar, las variancias de la aptitud combinatoria general y específica son estimaciones de la variancia genética aditiva y de la variancia de la dominancia, respectivamente, de esa población (despreciando la epistasia). Cuando se seleccionan varios clones para un huerto de semillas el mejorador está interesado principalmente en la aptitud combinatoria general, ya que por medio de tal huerto sólo puede sacar provecho de la variancia genética aditiva. En otros casos, sin embargo, puede ser también posible el uso de la aptitud combinatoria especifica, por ejemplo, con especies arbóreas que como Betula y Alnus permiten la producción de semilla en gran escala de sólo dos clones.
Correlaciones genéticas
Las correlaciones genéticas entre dos o más caracteres entrañan dos consecuencias para el mejorador de árboles: puede hacer uso de esta correlación por medio del llamado Frühtests o «ensayo precoz» si los árboles jóvenes manifiestan uno de los caracteres correlacionados y el otro sólo puede ser apreciado en árboles maduros. Por otro lado, la correlación genética puede conducir a cambios de caracteres no sometidos a selección.
La correlación de valores fenotípicos no prueba la presencia de correlaciones genéticas. Siendo
P = G + E
tal correlación puede resultar de una correlación de desviaciones ambientales. De ahí que la correlación genética sólo pueda ser estimada en experimentos en que G y E se dan separadamente.
Pueden originarse correlaciones genéticas por efectos génicos aditivos, de dominancia y epistáticos. Aquí sólo nos conciernen las correlaciones de «valores de mejora»originados por efectos aditivos. Este tipo resulta de la acción pleiotrópica de los genes por la cual idénticos genes afectan a ambos caracteres. (También pueden existir otros genes que afecten solamente a uno de los dos caracteres.)
La correlación genética hallada en un experimento de primera generación con árboles forestales es susceptible muchas veces de otras explicaciones. Puede resultar de ligamientos o de seleccionar el material en una población subdividida. Se sospecha que al menos algunos de los casos registrados de correlaciones genéticas en árboles forestales pertenecen a aquellas dos categorías. Es difícil determinar el tipo de correlación genética a base de un experimento de una generación.
En una experiencia con dos abedules japoneses Betula japonica y Betula maximowicziana, pudo separarse la correlación genética debida a subdivisión de las poblaciones. La experiencia contenía un cierto número de descendencias cada una de un árbol, de cada una de 12 y 15 subpoblaciones respectivamente, tomando muestras en las partes comunes del área natural de las especies. Se consideraron dos caracteres, época de foliación y de cese del crecimiento anual, medidos en un experimento en bloques aleatorios con cuatro repeticiones.
Se encontraron correlaciones muy significativas intrasubpoblaciones y de las medias de subpoblación en B. maximowicziana y ninguna en B. japonica. En B. maximowicziana aún queda un valor significativo del cuadrado medio después de eliminar la covariancia. Esto da la impresión de una correlación por ligamiento. Esta impresión es reforzada por el hecho de existir clines paralelos para ambos caracteres en B. maximowicziana pero sólo para el cese de crecimiento en B. japonica (Stern, 1963). Debe hacerse referencia también a Kimura (1960) para sistemas genéticos conducentes a ligamiento.
H. van Buijtenen (1963) y Sakai y Hatakeyama (1963) han dado cuenta recientemente de otras correlaciones genéticas en especies forestales.
Coeficiente de consanguinidad
Un cambio en el sistema de apareamiento en una población que lo tiene al azar conduce a consanguinidad, que puede ser medida de forma sencilla mediante el «coeficiente de consanguinidad» F de S. Wright (1921) y Malécot (1948).
La consanguinidad también juega un papel en las poblaciones naturales de las especies forestales. Esto ha sido investigado frecuentemente desde que J.W. Wright (1952) lo aseveró por primera vez (Langer 1952, Wang et al., 1960, y otros). En una población que tenga la estructura descrita anteriormente en este capítulo, la variación entre subpoblaciones ofrece un medio de investigar el grado de consanguinidad. De acuerdo con S. Wright (1921), en tales poblaciones
2 FVA
es la variancia genética esperada entre subpoblaciones, (siendo VA la variancia genética debida a efectos genéticos aditivos), y
(1 - F) VA
es la de la variancia genética esperada dentro de las subpoblaciones, admitiendo que VA es la parte preponderante de VG.
Se conoce muy poco sobre los valores numéricos que puede tomar F en un caso concreto. Los datos del Cuadro 1 fueron sacados de los dos experimentos de vivero con los abedules japoneses anteriormente mencionados.
Betula japonica es una especie «oportunista» de acuerdo con MacArthur (1960) y por ello es de esperar que muestre un más alto grado de consanguinidad que la especie «equilibrada» B. maximowicziana.
CUADRO 1. - COEFICIENTE DE CONSANGUINIDAD EN ESPECIES DE BETULA
|
Caracteres |
Año |
Coeficientes de consanguinidad F estimados por las dos ecuaciones dadas anteriormente |
|
|
B. japonica |
B. maximowicziana |
||
|
Cese de crecimiento |
1960 |
0,1215 |
0,0506 |
|
|
1961 |
0,1248 |
0,0100 |
|
Foliación |
1961 |
0,0844 |
0,0150 |
|
|
1962 |
0,1202 |
0,0268 |
|
Crecimiento en altura hasta |
1961/1962 |
0,1542 |
0,0497 |
|
|
1963 |
0,1424 |
0,0346 |
|
Roya de la hoja, registrada en verano |
1960 |
0,1024 |
- |
|
otoño |
1960 |
0,1030 |
- |
|
otoño |
1961 |
0,1745 |
- |
Es posible evitar el sesgo por consanguinidad en las estimaciones de h², si la magnitud de F es aproximadamente conocida. Dicho sesgo varía con el procedimiento empleado para determinar VA, lo que se debiera tener en cuenta al escoger el diseño de apareamiento (véase más abajo) si se desconoce el valor de F para la población en cuestión.
El grado de subdivisión de las poblaciones dentro de una región es por el momento desconocido para cualquier especie forestal. Sólo últimamente han sido preparados o establecidos experimentos que darán alguna información sobre ello. A continuación se relacionan aquellos de los que se tiene noticia.
Libby (1962) y Bannister (1963), Pinus radiata;
Zobel y McElwee (1960), Pinus taeda;
J. W. Wright (1961), Pinus sylvestris y Pinus nigra;
Langlet (1959) y Kuratorium für Forstpflanzenzüchtung (1962), Picea abies;
Morgenstern (com. pers.), Picea mariana;
Stern (1961), Betula japonica y B. maximowicziana.
En todas estas experiencias se reconoce que el mejorador de árboles forestales necesita una información más completa de las poblaciones a las que desea aplicar métodos de genética cuantitativa. No se pueden discutir aquí los diferentes diseños experimentales, aunque ellos hubieran mostrado los distintos puntos de vista desde los que se pueden emprender tales experimentos.
La consanguinidad es importante también en un programa de mejora a consecuencia del fenómeno conocido como «depresión de consanguinidad». Como solamente un número limitado de individuos pueden admitirse en cada generación, los individuos de generaciones posteriores se van emparentando cada vez más. Se ofrecen dos posibilidades al mejorador para contrarrestar este proceso. Puede, o bien mantener una población bastante grande, o bien controlar las ascendencias de los genitores en cada generación. Se ha escrito mucho sobre consanguinidad en árboles forestales, empezando con la publicación de Sylvén (1910) y existen pocas dudas sobre su importancia. El número mínimo de clones ha sido calculado por Stern (1959) mientras que Langner (1961) ha demostrado que la depresión por consanguinidad en el Larix es una función lineal de F, como se esperaba teóricamente.
Dísenos de apareamiento
Los parámetros genéticos cuantitativos de una población sólo pueden ser estimados a través de experimentos de campo. Desgraciadamente, rara vez es posible establecer experimentos particulares con este fin. Por esto, es aconsejable en el momento presente establecer experimentos de campo que sirvan a varias finalidades. Estas son:
1. conseguir información sobre la aptitud combinatoria general y específica de genitores para huertos de semillas;2. conseguir estimaciones que sean de fiar de los parámetros genéticos;
3. establecer material para trabajo ulterior de mejora.
Además, las áreas experimentales deben ser suficientemente pequeñas para mantener los gastos dentro de límites tolerables.
El primer paso al planear las pruebas de descendencia es la elección de un diseño adecuado de apareamiento. En la mayoría de los casos, el elegido será una variante de la tabla dialela (Andersson, et al. 1951; Zobel y Mc Elwee, 1960 y otros). Realmente un experimento de campo con descendencias de un cruzamiento dialelo, si está bien planeado, da toda la información necesaria y se mantiene suficientemente pequeño.
El dialelo puede ser completo o incompleto (Hinkelmann, 1960). Puede tener la forma de una serie de prueba, conteniendo un reducido número de clones comprobadores y un número elevado de clones a comprobar, digamos b clones comprobadores B y c clones a comprobar C. En tal experimento, plantado en bloques aleatorios, el análisis de variancia de las medias por parcela será como indica el Cuadro 2.
CUADRO 2. - FORMA DE ANÁLISIS DE VARIANCIA DE MEDIAS POR PARCELA
|
Fuentes de variación |
Grados de libertad |
Cuadrado medio esperado |
|
Bloques |
r - 1 |
VE + bcVR |
|
Aptitud combinatoria general B |
b - 1 |
VE + rVBC + rcVB |
|
Aptitud - combinatoria general C |
c - 1 |
VE + rVBC + rbVc |
|
Aptitud combinatoria específica. |
(b - 1) (c - 1) |
VE + rVBC |
|
Error |
(r - 1) (bc - 1) |
VE |
|
TOTAL |
rbc - 1 |
|
Presumiendo que los genitores en ambas series de clones se han tomado aleatoriamente de una población con apareamiento al azar, VO proporciona una estimación de ¼de la variancia genética aditiva V., y VBC una estimación de ¼ VD de aquella población apareada al azar (siendo VD la parte de la variancia genética debida a efectos de dominancia de los genes). Si el origen del material no puede ser definido de manera correcta, se puede llamar a VC la variancia de la aptitud combinatoria general de los clones de la serie C.
Aceptando el modelo de población dado anteriormente en este capítulo y la selección de clones hecha sobre toda la región, puede afirmarse que
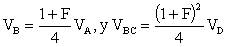
No serán tenidas en cuenta aquí otras situaciones.
Se han sugerido otros diseños de acoplamiento distintos de la tabla dialela. Gustafsson (1949) recomienda el empleo de una mezcla de polen como genitor comprobador. Bajo la suposición del apareamiento al azar en una población, la variancia de las medias familiares da entonces una estimación de ¼ VA. Schröck, en una comunicación personal, emplea un solo genitor masculino o femenino como comprobador. La variancia de las medias familiares será entonces ¼ VA + ¼ VD, siempre que la estructura de la población sea de apareamiento al azar.
Las descendencias de un árbol en polinización libre deberán dar la misma variancia interfamiliar que el policruzamiento de Gustafsson. Pero en este caso parece ser un poco precaria la suposición de polinización al azar (Squillace et al., 1961).
El mejorador debe elegir cuidadosamente los diseños de apareamiento. Está decidiendo ya, en esta fase temprana, sobre la clase de información que sacará en el futuro, sobre el tamaño del ensayo en el monte y sobre las posibilidades de trabajos ulteriores con descendencias de ese experimento.
Otro método de obtener estimaciones de VA lo proporciona el hecho de que la regresión de la expresión de un carácter en genitores y descendencia es debida completamente a VA. Finalmente, Shrikhande (1957), Sakai y Hatakeyama (1963) y Freeman (1963) presentan todos un método nuevo capacitando al mejorados de árboles, bajo determinadas circunstancias, para estimar variancias genéticas y correlaciones genéticas en masas coetáneas sin necesidad de criar descendencias.
Experiencias de campo
La elección de diseño en el campo, tamaño de las parcelas y número de repeticiones determina la eficiencia de un experimento, esto es, la cantidad de información que se habrá de obtener. Hasta ahora no hay muchos datos sobre la eficiencia de las experiencias de monte con árboles forestales, pero los estudios de J. W. Wright y Freeland (1960), Evans et al. (1961) y Strand (1955) prueban todos que las ideas fundamentales admitidas por Andersson et al. (1951) eran correctas.
Son de esperar en el mismo experimento variancias diferentes del error para caracteres distintos. Las heredabilidades dadas en el Cuadro 3 fueron obtenidas en un ensayo con 100 procedencias de Picea abies. El diseño fue seudo-factorial simple (lattice simple) con 4 repeticiones, parcelas de 5 por 5 plantas, espaciadas 1,1 m. X 1,1 m:
CUADRO 3. - HEREDABILIDADES OBTENIDAS EN UN ENSAYO DE PROCEDENCIAS DE Picea aojes
|
|
Número de repeticiones | |||||||
|
Carácter |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Foliación en 1962 |
87 |
93 |
95 |
96 |
97 |
98 |
98 |
98 |
|
Daños por helada de primavera 1961 |
93 |
97 |
98 |
98 |
99 |
99 |
98 |
99 |
|
Crecimiento en altura |
39 |
67 |
66 |
72 |
77 |
79 |
82 |
84 |
|
Formación de prolepsis 1962 |
39 |
56 |
66 |
72 |
70 |
79 |
82 |
84 |
Una sola repetición daría el 87 y el 93 por ciento de la información disponible tratándose de la foliación y daños por helada, respectivamente; pero el crecimiento en altura y la formación de prolepsis muestran heredabilidades mucho menores. Solamente con 8 repeticiones se podría lograr un 84 por ciento de heredabilidad. Estas cantidades fueron obtenidas sin tener en cuenta los bloques incompletos. Eliminando la variancia entre ellos la eficiencia alcanzaría el 156 por ciento de la de bloques aleatorios.
Sería de desear que, siguiendo las proposiciones de Evans et al. (1961), todos los resultados disponibles de experiencias de campo fuesen recogidos y preparados para difusión, sobre parcelas de tamaño óptimo, número óptimo de repeticiones, etc. Además, las pruebas debieran ser algo más uniformes, similares a las de J. W. Wright y Freeland (1960) o Strand (1955), en diferentes localidades y con diferentes especies arbóreas. Entonces sería posible acumular en pocos años suficiente material para la planificación de experiencias de campo. Interacciones de genotipo y ambiente.
El mejorador de árboles trabaja en una región o selecciona árboles en regiones que son en cierta medida heterogéneas en cuanto a suelo y clima. Además, las condiciones atmosféricas cambian de un año para otro, y en años de condiciones extremas pueden ser invalidados los resultados previos de muchos años. El mejorador debe tener en cuenta el hecho de que genotipos diferentes pueden reaccionar diversamente en ambientes distintos. Deberá repetir sus pruebas en varios sitios y, si es posible, durante varios años. Por ejemplo, una serie de pruebas tales un dialelo A x B en 1 localidad con r repeticiones, cada una diseñada en bloques aleatorios, proporciona las expectativas del Cuadro 4.
CUADRO 4. - FORMA DE ANÁLISIS DE 1: AS INTERACCIONES ENTRE GENOTIPO Y AMBIENTE
|
Fuente de variación |
Cuadrado medio esperado |
|
A |
VE + rVABL + rlVAB + rbVAL + rblVA |
|
B |
VE + rVABL + rlVAB + raVBL + ralVB |
|
A X B |
VE + rVABL + rlVAB |
|
L |
VE + rVABL + rbVAL + raVBL + rabVL |
|
A X L |
VE + rVABL + rlVAB + rbVAL + rblVA |
|
B X L |
VE + rVABL + raVBL |
|
A X B X L |
VE + rVABL |
|
R within L |
VE + abVR |
|
E |
VE |
Entonces la heredabilidad tiene que ser tomada de todas las localidades. Por ejemplo, si los clones a probar consisten en la muestra A:
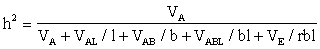
Los sitios de ensayo no deben ser elegidos al azar como ocurre frecuentemente. Deben preferirse los sitios más representativos.
Desgraciadamente hay pocos datos sobre las interacciones genotipo x ambiente en experiencias de campo con material obtenido por mejora selectiva de árboles forestales, y estos datos no son muy de fiar.
Competición
La competición es la influencia mutua de los pies dentro del rodal y tiene las siguientes consecuencias para el mejorador de árboles.
1. La selección de árboles plus resulta poco segura para los caracteres afectados por la competición.2. Las estimaciones de la aptitud combinatoria y de las variancias genéticas se sesgan en cierto grado debido a la competición dentro de y entre las parcelas.
Hasta ahora no ha sido suficientemente comprendido el fenómeno de la competición a pesar de algunas publicaciones fundamentales que se refieren a ella (Sakai, 1955; Symp. Soc. Exp. Biol. Cambr. 1961).
Se debe en parte a la competición, el que las heredabilidades de crecimiento obtenidas de las regresiones entre genitores y descendencia sean considerablemente más pequeñas que las obtenidas del análisis de hermanos con uno o los dos genitores comunes. Puede admitirse que las últimas heredabilidades son más seguras.
Es difícil de apreciar la competición en pruebas de descendencia. Si las familias se plantan en parcelas, compiten entre sí principalmente plantas con uno o los dos genitores comunes. Por otro lado la descendencia de un huerto para semilla en la cual ha sido hecha selección consistirá prácticamente en individuos sin parentesco. Entonces la competición es de otro tipo diferente. Por esta razón la mayor parte de los mejoradores de árboles prescinden de fajas aisladoras y parcelas grandes, usuales en otras ramas de la investigación forestal.
Los resultados de Snaydon (1961) muestran que es necesario considerar la aptitud competitiva de diferentes genotipos. No halló diferencias entre ecotipos de diferentes suelos cuando crecían por parcelas; pero siempre presentaba superioridad un ecotipo sobre su propio suelo cuando se les dejaba competir unos con otros. Experimentos más antiguos de Sukatschew (1927) insisten en la misma dirección. Por esto la competición puede causar en parte la subdivisión dentro de una región.
Recientemente, (1963) presentó un nuevo y prometedor método para la estimación de heredabilidades en presencia de competición. Debiera investigarse más a fondo este problema, que es de vital importancia no sólo para la mejora genética forestal sino también para otros aspectos de la investigación y práctica forestal.
Significado de ganancia genética
Cuando por selección se crea una nueva población, su valor genético medio difiere del valor de la población original. Esta diferencia es la «ganancia genética»específica del método e intensidad de selección empleada en un programa de mejora genética particular. Por supuesto, cada mejorador intenta hacer dicha diferencia lo más grande posible.
Tres factores determinan la ganancia obtenido o esperada:
1. la variancia genética que es la base de cualquier selección;2. la precisión de las estimaciones de los valores de mejora tanto en la selección de individuos superiores en una masa como familias en una experiencia, expresados por la heredabilidad;
3. la intensidad de selección, esto es, la diferencia entre la media poblacional y el promedio de los individuos seleccionados.
Puede demostrarse que bajo determinadas condiciones la ganancia genética R viene dada por la siguiente ecuación:
R = h² S
en la que S es la diferencia entre las medias de las poblaciones original y seleccionada. Esta es la fórmula básica para cualquier estimación de la ganancia genética esperada.
Indices de selección
El valor económico de un cultivar está determinado por varios caracteres. De ahí que sea necesario buscar un procedimiento de selección que tenga en cuenta la complejidad de la situación y dé los mejores resultados posibles, no por un carácter único sino por todo el complejo de caracteres que dan lugar al valor económico. El mejor procedimiento para lograrlo parece ser el índice de selección. El más completo examen del problema ha sido hecho por Le Roy (1960).
Al formar los índices de selección es necesario combinar los valores económicos de los distintos caracteres, sus heredabilidades y sus correlaciones con otros caracteres de importancia económica. Se admite que para disponer de correlaciones genéticas son necesarios ensayos de descendencia muy completos. Supóngase un programa de selección en el que el mejorador seleccione por los caracteres x1, Xn. Supóngase además que las heredabilidades, las correlaciones genéticas y el peso económico de todos los caracteres sean conocidos. Es posible combinar todos estos datos en un índice único que toma la forma de una regresión múltiple, pero que se calcula de forma diferente (para más detalles, véase Le Roy 1960):
I = b1x1 + b2x2... + bnxn
b1... bn son los pesos de los caracteres por separado. Si un carácter tiene una importancia económica grande tendrá también un peso grande. Pero esto puede ser contrarrestado por una heredabilidad baja o por una correlación genética negativa con otros caracteres de importancia económica. Por esto se emplean ambas informaciones, económica y genética, para calcular los b1... bn.
La ecuación para determinar la ganancia genética puede aplicarse también al índice de selección, esto es, selección por valores elevados de I. No obstante, es difícil de resolver en algunos casos el problema de determinar el método de selección óptimo para una serie dada de pesos económicos y parámetros poblacionales. Han tenido éxito intentos hechos en la mejora animal, abordando el problema con calculadores de gran rapidez y poblaciones modelo. Este método podría ser interesante para resolver ciertos problemas de la mejora genética forestal.
Por supuesto, el valor económico de un carácter es de naturaleza problemática. Se altera con el cambio de las condiciones del mercado. Ello no obstante, es posible ponderar económicamente los diversos caracteres combinados en el índice. Rapidez de crecimiento, derechura del tronco, buena poda natural, etc. son caracteres que es de esperar conserven su valor por largo tiempo.
La aspiración a meter tantos caracteres como sea posible dentro del Índice es contrarrestada por el hecho de que cada nuevo carácter considerado disminuye la intensidad de selección de los otros. Por esto el mejorador tiene que restringir- el número de caracteres a seleccionar, lo que refuerza la necesidad de proceder a una ponderación deliberada para escoger los caracteres más importantes.
Hasta ahora sólo ha sido confeccionado un índice de selección «real» para uso en la mejora de árboles forestales por J. P. van Buijtenen y van Horn (1960). Sin embargo, los sistemas de puntuación usados por la mayoría de los mejoradores de árboles son también índices de selección. La confección de los índices y su ajuste continuo a las condiciones del mercado es uno de los problemas más importantes de los mejoradores. Sólo puede darse una solución a este problema en cooperación estrecha con economistas forestales.
Puesto que la heredabilidad de un carácter puede ser baja en las masas, pero alta en una experiencia de campo bien planeada, el poso de tal carácter será diferente en un índice de selección calculado para hacer máxima la ganancia por selección de árboles plus comparado al que tendría en un segundo índice que se refiera al mismo carácter y a la misma población, pero a una selección a base de pruebas de descendencia. Nixon y Moffet (1963) dan un buen ejemplo de esto.
Factores determinantes de la ganancia genética
El objetivo de todo mejorador es sacar el máximo partido posible de los medios disponibles. Normalmente esto es idéntico a lograr la máxima ganancia genética (en valores de índice) por unidad de tiempo. Para las plantas anuales y también para muchas especies animales se considera como unidad de tiempo una generación.
Para los árboles forestales, sin embargo, una generación representa un período variable. Su duración está determinada por:
a) el tiempo transcurrido entre la polinización y la recogida de la semilla, que puede durar dos o aun más años;b) el tiempo transcurrido desde la recogida de la semilla hasta el final de las experiencias de campo, que puede variar considerablemente;
c) el tiempo necesario para aplicar los resultados de la selección a la práctica forestal.
El mejorador intenta, por supuesto, acortar cada período en lo posible. Puede combinar varias medidas durante los diferentes períodos. Dado que en la mejora selectiva cada paso es seguido por otros, es necesario prever también los progresos posibles en pasos posteriores. Por esto, además del índice selectivo una porción de hechos deben ser tenidas en cuenta ya que también ellos ejercen influencia en el éxito de un programa de selección. En lo que concierne a esta clase de consideraciones da la impresión de que estamos apenas en el comienzo.
Ensayo precoz
Los caracteres que poseen una heredabilidad en sentido estricto muy elevada pueden seleccionarse por medio de la selección de árboles plus. En tal caso una gran diferencial selectiva garantiza un rápido progreso a través de la selección en masa sin pruebas de descendencia.
No es lo mismo cuando la selección de varios caracteres necesita para ser segura basarse en pruebas de descendencia. A causa de los grandes costes de tales pruebas, es deseable reducir su tamaño a dimensiones practicables, si bien en ensayos más pequeños se pierda probablemente la oportunidad de tener una gran diferencial selectiva. Por este motivo se ha intentado utilizar por selección indirecta las correlaciones genéticas entre caracteres de plantas jóvenes y aquellos que sólo se acusan en los estados más tardíos del desarrollo del árbol. (Para un resumen sobre este tema véase Schmidt 1957.)
El éxito de tal selección indirecta comparado con el de la selección directa, puede expresarse en la siguiente forma (Falconer, 1960):
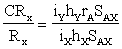
En esta ecuación CRx representa la respuesta en x correlacionada a la selección por y, Rx la respuesta a la selección directa por x, iy e ix las intensidades de selección de y y x respectivamente, hx y hY las raíces cuadradas de las heredabilidades, rA la correlación de los valores dé mejora en x e y, y sAX la desviación típica de los valores de mejora de x.
Las afirmaciones sobre correlaciones genéticas hechas anteriormente en este capítulo sirven también para los «ensayos precoces». En particular, debe considerarse que las correlaciones debidas a ligamiento cambian de una generación a otra, y que las correlaciones debidas a subdivisión de las poblaciones carecen de toda utilidad en la selección indirecta dentro de subpoblaciones.
Huertos para semilla
Durante los últimos años ha habido discusiones sobre el tipo más apropiado de huerto para semilla. En particular J. W. Wright (1959) y Goddard y Brown (1961) han llamado la atención hacia los huertos para semilla, constituidos por planta nacida de semilla eligiendo los mejores árboles de las mejores descendencias de las pruebas de descendencia. Este concepto de huerto para semilla es completamente diferente del constituido por clones, desarrollado especialmente en Suecia.
El objeto de este capítulo ha sido mostrar que son necesarios gran cantidad de conocimientos para poder deducir el procedimiento de selección más provechoso. Puede darse por seguro que no existen actualmente suficientes datos para desarrollar un programa de selección de ninguna especie arbórea forestal, particularmente sobre:
a) heredabilidades para masas y cierto tipo de ensayos de procedencias;
b) correlaciones genéticas de los más importantes caracteres;
c) efecto de la consanguinidad;
d) interacciones genotipo x ambiente;
e) ponderación económica de caracteres importantes;) tiempo requerido para cada etapa del programa.
Por ahora es necesario adivinar o estimar estos datos subjetivamente, procedimiento que parece algo dudoso. Un procedimiento experimental conducente a la selección de material superior y que proporcione estimaciones de los parámetros genéticos parece ser el más prometedor.
Aparte de esto difícilmente podría aceptarse un tipo general de huerto para semilla clonal apto para todas las especies y programas de mejora. El concepto sueco es muy flexible. Se puede lograr mucho eligiendo un programa de etapas adecuado, cometido en el que pueden ayudar los métodos de la genética cuantitativa.
Hoy por hoy, el valor de la genética cuantitativa descansa en que ofrece una base para planificar eficientemente experimentos en las primeras etapas de los programas de selección.
ANDERSON, R. L. 1960. Uses of variance component analysis in the interpretation of biological experiments. Bull. Int. Stat. Inst. 37. 22 P.
ANDERSSON, E., GUSTAFSSON, A. s; JOHNSSON, H. 1951. Avkomme-prövning i skogsbrukets tjänst [Use of progeny trials in forestry]. Norrlands Skogsv. Förb. Tidskr., 4: 37-409.
BAKER, H. G. 1959. Reproductive methods as factors in speciation in flowering plants. Cold Spring Harbor Symp., 24: 177191.
BANNISTER, M. H. 1963. Planning a genetical survey of Pinus radiata populations. FAO/FORGEN, 63-5/1.
BUIJTENEN, H. VAN. 1963. Heritability of wood properties and their relation to growth rate in Pinus taeda. FAO/FORGEN, 63-7/2.
BUIJTENEN, J. P. VAN & HORN, W. M. VAN. 1960. A selection index for aspen based on genetic principles. Prog. Rep. No. 6, Lake States Aspen Gen. and Tree Impr. Group, Appleton, Wisconsin.
CALLAHAM, R. Z. 1963. Provenance research. FAO/FORGEN, 63-3/0. (Chapter 4)
EVANS, T. C., BARBER, J. C. & SQUILLACE, A. E. 1961. Some statistical aspects of progeny testing. Proc. 6th Southern For. Tree Impr. Cont., p. 73-79.
FALCONER, D. S. 1960. Introduction to quantitative genetics. New York, Ronald Press; Edinburgh, Oliver & Boyd.
FREEMAN, G. H. 1963. The combined effect of environmental and plant variation. Biometrics, 19: 273-277.
GODDARD, R. E. & BROWN, C. L. 1961. An examination of seed orchard concepts. J. For., 59: 252-256.
GUSTAFSSON, A. 1949. Conifer seed plantations. Their structure and genetical principles. In Proc. 3rd World For. Congr., Helsinki, p. 117-119.
HANSON, W. 1961. Heritability. Symp. on Statistical Gen. and Plant Breeding, Raleigh, N. C.
HATTEMER, H. E. 1963. Estimates of heritability published in forest tree breeding research. FAO/FORGEN, 632a/3.
HINKELMANN, K. 1960. Krenzongspläne zur Selektionezüchtung bei Waldbäumen. Silvae Genet., 9: 121-148.
KIMURA, M. A. 1960. Model of a genetic system which leads to closer linkage by natural selection. Evolution, 14: 278-287.
Kuratorium für Forstpflanzenzüchtung. 1962. Vorschlag für einen Fichten Herkunts-Versuch. Mimeogr.
LANGLET, O. 1936. Studien über die physiologische Variabilität der Kiefer und deren Zusammenhang mit dem Klima. Beiträge zur Kenntnis de Ökotypen von Pinus sylvestris L. Medd. Statens skogsforskn. Inst. Stockh., 29: 219-470.
LANGLET, O. 1959. Skogsforskningens nya granproveniensförsök [New experiments in spruce provenance research]. Skogen (18): 370-371.
LANGNER, W. 1952-53. Die diagnostische Bedeutung eines aurea Faktors bei Picea abies fur die genetisch wirksame Pollenverteilung. Z. Forstgenet., 2, 21-22.
LANGNER, W. 1961. Einige Versucheergebuisse zum Inzuchtproblem bei der forstlichen Saatguterzeugung. Proc. 6th IUFRO Congr., Vienna.
LE ROY, H. L. 1960. Statistische Methoden de Populationagenetik. Basel und Stuttgart, Birkhäuser.
LIBBY, W. J. 1962. Research proposal. Mimeogr.
LUSH, J. L. 1937. Animal breeding plans. First ed. Ames, Iowa State Coll. Press.
MACARTHUR, R. 1960. On the relative abundance of species. Amer. Nut., 94: 25-34.
MALÉCOT, G. 1948. Les mathématiques de l'hérédité. Paris, Masson.
MERGEN, F. 1960. Variation and heritability of physiological and morphological traits in Norway spruce. Proc. 5th World For. Congr., Seattle, USA.
NIXON, K. M. & MOFFETT, A. A. 1963. One part progeny testing in black wattle (Acacia mearnsii, de Wild). FAO/FORGEN, 63-2a/5.
SAKAI, K. I. 1955. Competition in plants and its relation to selection. Cold Spring Harbor Symp., 20: 137157.
SAKAI, K. I. & HATEKEYAMA, S. 1963. Estimation of genetic parameters in forest trees without raising progenies. FAO/FORGEN, 63-2a/4.
SCHMIDT, W. 1957. Die Sicherung von Frühdiagnosen bei lang lebigen Gewächsen. Züchter, 4, suppl.: 39-69.
SHRIKANDE, V. J. 1957. Some considerations in designing experiments on coconut trees. J. Indian Soc. Agr. Stat., 1: 82-88.
SNAYDON, W. R. 1961. Competitive ability of natural populations of Trifolium repens and its relation to differential response to soil factors. Heredity, 16: 522.
SOCIETY OF EXPERIMENTAL BIOLOGY, CAMBRIDGE. 1961. Competition and co-operation. S.E.B. Symp. 15.
SERAQUE, G. F. s; TATUM, L. A. 1942. General versus specific combining ability in single crosses of corn. J. Amer. Soc. Agr., 37: 923-932.
SQUILLACE, A. E. si BENGTSON, G. W. 1961. Inheritance of gum yield and other characteristics of slash pine. Proc. 6th Southern Tree Impr. Conf., p. 85-96.
SQUILLACE, A. E. & DORMAN, K. W. 1961. Selective breeding of Slash pine for high oleoresin yield and other characters. Abstract in Proc. 9th Int. Bot. Congr., Montreal, Vol. 2 (375).
STEBBINS, G. L. 1950. Variation and evolution in plants. New York, Columbia University Press.
STERN, K. 1959. Der Inzuchtgrad in den Nachkormnenschaften von Samenplantagen. Silvae Genet., 8: 37-42.
STERN, K 1961. Preliminary estimates of the genetic structure of two sympatric populations of birches as determined by random effects and natural selection. Proc. 9th Northeastern Tree Impr. Conf., Syracuse, N. Y., U.S.A., p. 25-34.
STERN, K. 1963. Über einen Altitudinalklin in zwei japanischen Birkenarten. Festschrift der Darre, Laufen/Obb. (In press)
STRAND, L. 1955. Plot sizes in field trials. Z. Forstgenet., 4: 156162.
SUKATSCHEW, W. N. 1927. Einige experimentelle Untersuchun gen über den Kampf ums Dasein zwischen Biotypen derselben Art. Z. Ind. Abst. Verb. Lehre, 47: 54 p.
SYLVÉN, N. 1910. Om pollineringsförsök med tall och gran [Experiments in self-pollination with pine and spruce]. Medd. Statens skogsförsöknsanstalt, 7: 219-228.
TODA, R. 1963. Mass selection and heritability studies in forest tree breeding. FAO/FORGEN, 63-2a/2.
WANG, C. W., PERRY, T. O. & JOHNSSON, A. G. 1960. Pollen dispersion of Slash pine (Pinus elliottii) with special reference to seed orchard management. Silvae Genet., 9: 78-86.
WRIGHT, J. W. 1952. Pollen dispersion of some forest trees. Northeastern For. Exp. Sta. Paper No. 46.
WRIGHT, J. W. 1959. Seed orchards or test plantings? In Recent advances in botany. Univ. of Toronto Press.
WRIGHT, J. W. 1961. Geographic variation patterns in forest trees. 2nd Central States For. Tree Impr. Conf., Franklin Park, III: 15-20.
WRIGHT, J. W. & FREELAND, F. D. 1960. Plot size and experimental efficiency in forest genetic research. Mich. State Univ. Agr. Exp. Sta., Tech. Bull. 280. 28 p.
WRIGHT, S. 1921. Systems of mating. Genetics, 6: 111-178.
WRIGHT, S. 1955. Factors of evolution. In Cold Spring Harbor Symp., 20: 16-24.
ZOBEL, B. & MCELWEE, R. 1960. Plans for progeny testing seed orchards. Mimeogr.