3.1 COMPLETE ENUMERATION (CENSUS)
3.2 CENSUS IN SPACE, SAMPLING IN TIME
3.3 CENSUS IN TIME, SAMPLING IN SPACE
3.4 SAMPLING IN SPACE AND IN TIME
In the numerical example given earlier, which applied the generic approach for estimating total catch, it was assumed that total fishing effort was known. There are four approaches to the estimation of fishing effort: 1) complete enumeration through census of fishing activities; 2) census in space and sampling in time; 3) sampling in space and census in time; and 4) sampling in both space and time. Their applicability depends on the local conditions within the region as well as on the human capacity to conduct the required data collection operations.
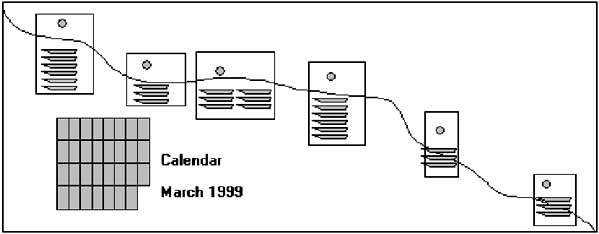
3.1.1 An illustrated example
The figure above illustrates the census approach for calculating fishing effort. All features are shaded - all fishing sites along the coast, all boats at each fishing site and all calendar days - indicate that a complete enumeration is required in both space and time.
3.1.2 Type of survey
Complete enumeration of fishing effort implies that at the end of the reference period (i.e. a calendar month) the survey field teams have enumerated all fishing trips performed by all fishing units during that period.
3.1.3 Feasibility
This approach is feasible when:
3.1.4 Evaluation of census approach
Since complete enumeration covers all sites, vessels and days, the census approach is not strictly sampling (although it may be an approach used for Frame Surveys, see section 8.) and contains no sampling errors.
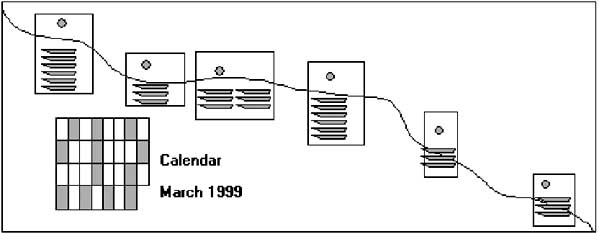
3.2.1 An illustrated example
In the figure above all fishing sites and boats are shaded to indicate that they have been enumerated. Blank boxes in the calendar show that recording was not performed on all days.
3.2.2 Type of approach
This approach is similar to the census approach but with a limited number of days during which data is collected, thus achieving some reduction in data collection effort.
3.2.3 Estimation process
At the end of the month total fishing effort is estimated as:

where:
3.2.4 Reliability of estimate
Reliability of the estimate for fishing effort depends on:
3.2.5 Applicability
The census in space - sampling in time approach is recommended when:
3.2.6 A numerical example
In January 2001 a complete enumeration of fishing effort at all locations was conducted on each of 10 pre-selected days, excluding four Sundays during which it was known that no fishing took place.
E = AverE x A = 1,000 × 27 = 27,000 boat-days.
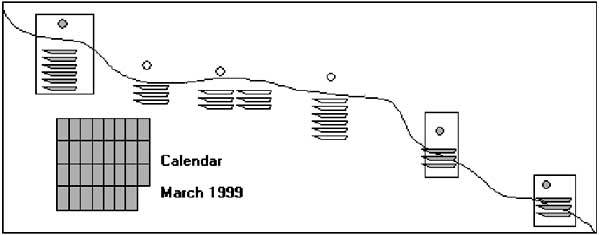
3.3.1 An illustrated example
Census in time and sampling in space is illustrated in the figure above. Three fishing sites are shaded as participating in the samples. Sampling at these three sites takes place every day, as indicated in the shaded boxes in the calendar.
3.3.2 Type of approach
In this approach it is assumed that the fishing units are much dispersed over the statistical area and no mechanism exists for obtaining effort data from all fishing sites.
3.3.3 Staff time
It is also assumed that there is availability of staff time for daily collection of information from the selected sampling locations; i.e. data recorders resident at fishing sites.
3.3.4 Estimation process
At the end of the month total fishing effort is estimated as:

where:
3.3.5 Reliability of estimate
The reliability of the estimate for fishing effort depends on:
3.3.6 Applicability
The census in time - sampling in space approach is recommended when:
3.3.7 Evaluation of approach
This approach is less robust because the raising factor F must be obtained through a frame survey which is conducted, at best, on a yearly basis. In comparison to scenario 3.2 discussed earlier, the time raising factor A is less “static” since it is formulated on a monthly basis.
3.3.8 A numerical example
A frame survey conducted in a statistical area in March 1998 reported the existence of 1,000 gillnet canoes operating from 20 fishing sites, i.e. F = 1,000.
During January 2001 daily data collection operations took place in four pre-selected sites with the view of calculating total fishing effort (in all fishing sites) related to 40 canoes operating from these sites.
The sampled 40 canoes was found to operate for 800 boat-days, thus the average effort of a single canoe during January 2001 was:
AverF = 800/40 = 20 boat-daysTherefore, total fishing effort is estimated as:
E = AverF × F = 20 × 1,000 = 20,000 boat-days
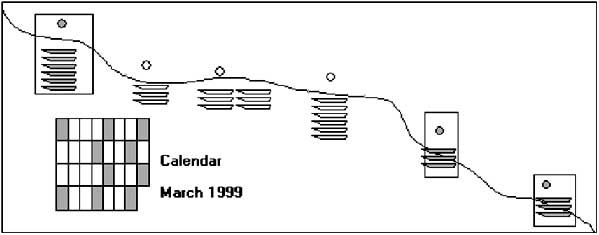
3.4.1 An illustrated example
In this approach three fishing sites are sampled over 10 days during the month.
3.4.2 Estimation
This is the commonest approach for estimating total fishing effort and is described by the following formula:

where:
3.4.3 A numerical example
Assume that in the province of Fako in Cameroun during April 2001 a fishing effort survey was conducted for gillnets. The last Fako frame survey was conducted in June 1999 and reported that there should be 500 canoes of this boat/gear category, that is F = 500.
A boat activity survey has revealed that in the province of Fako the probability of a gillnet canoe to be fishing on any given day during April 2001 was BAC=0.8 and that all days in the month ought to be considered without exception as days with fishing activities, i.e. A=30 days.
With this information available, fishing effort is computed as follows:
3.4.4 Comparison to other approaches
|
SUMMARY In this section four different approaches for the estimation of fishing effort were presented with the following characteristics: (a) When feasible the census approach is the most accurate in calculating total fishing effort (Approach 3.1). |