4.1 CENSUS COSTS AND OBJECTIVES OF SAMPLING
4.2 ACCURACY AND PRECISION IN SAMPLING
4.3 ACCURACY AS A FUNCTION OF SAMPLE SIZE
4.4 A PRIORI ACCURACY INDICATORS
4.5 SAFE SAMPLE SIZE FOR LANDINGS AND EFFORT
4.6 VARIABILITY INDICATORS
4.7 STRATIFICATION AND ITS IMPACT ON SURVEY COST
4.8 THE PROBLEM OF BIASED ESTIMATES
4.9 NEED FOR REPRESENTATIVE SAMPLES
4.10 THE “BOAT” AND “GEAR” APPROACHES
Choosing to undertake sample-based surveys is based primarily on the recognition that complete enumeration through census-based surveys imposes huge costs that are both unsustainable and unnecessary if the nature and methods of statistical sampling are properly considered. Such considerations include understanding of:
Census-based techniques are generally impractical in small-scale fisheries due to the large number of fishing operations that would have to be monitored over a reference period. The following example outlines the logistics problems and costs involved in census-based surveys.
Assume a fishery of moderate size comprising 1,000 fishing canoes, each fishing 24 times during a month on a one-day-per-trip basis. This would mean that:
1) There would be about 24,000 landings during the month and all landings would have to be recorded, each with its complete set of basic fishery data (species composition, weight, etc) (Note that there will be no need for a separate survey for fishing effort, since all trips will be recorded.)On the other hand a well-defined sampling scheme would most likely need only one or two recorders for data collection and only a fraction of the computer storage and processing resources, due to the much lower volume of incoming data.2) Assuming that a single recording of a landing would take a minimum of ten minutes (experience shows that this is the case in many data collection systems), a minimum of 240,000 minutes (4,000 work hours) will be needed.
3) If a data collector works 8 hours per day for 25 days in a month, then collection of data would require 4,000/8 × 25 = 20 data collectors just to monitor this relatively small fishery. This assumes that such a level of data collection is feasible and that landings and hence fisher availability is spread evenly over the day.
4) In addition to the costs of data collectors there would also be the costs of a) supervision, b) data editing, checking and inputting for 24,000 landings per month, and c) computer data storage for 12 x 24,000 = 288,000 landings per year.
Thus there are three objectives of a sampling programme:
In sampling procedures accuracy and precision are two different statistical indicators and it is perhaps worth clarifying their meaning at this point, as frequent reference will be made to these two terms in the coming sections.
4.2.1 Sampling Accuracy
4.2.2 Sampling Precision
Sampling precision is related to the variability of the samples used. It is measured, in reverse sense, by the coefficient of variation (CV), a relative index of variability that utilizes the sample variance and the sample mean.
The CV index also determines the confidence limits of the estimates, that is the range of values that are expected to contain the true data population values at a given probability.
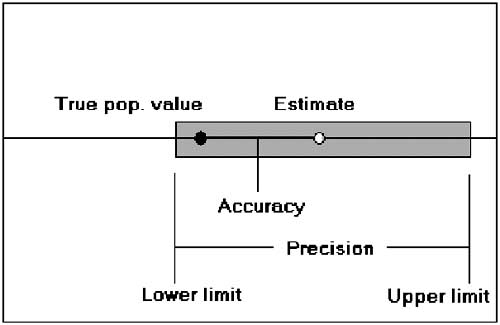
Estimates can be of high precision (that is with narrow confidence limits), but of low accuracy. This occurs when samples are not representative and the resulting estimates are lower or higher than the true data population value.
When sample size increases precision also increases as a result of decreasing variability. Its growth, very sharp in the region of small samples, becomes slower and steadier beyond a certain sample size.
The figure below illustrates the meaning of accuracy and precision. They are both important statistical indicators and regularly used for assessing the effectiveness of sampling operations. Their correct interpretation can greatly assist in identifying problem areas and applying appropriate corrective actions as necessary.
The following diagram illustrates the pattern of accuracy growth when sample size increases (see also table 4.5).
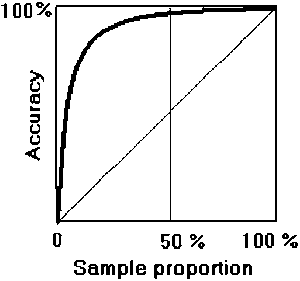
To be noted that:
A frequent concern of fishery administrations is the limited budgetary and human resources for data collection. Such constraints have direct impacts on the frequency and extent of field operations for data collection and demand the development of cost-effective sampling schemes. Therefore, during survey design it is better to establish accuracy indicators so that sample sizes can guarantee an acceptable level of reliability for the estimated data population parameters. This is at times difficult, since at the outset little may be known about the distribution and variability of the target data populations. Until some guiding statistical indicators become available statistical developers will tend to require large samples which increase the size and complexity of field operations and data management procedures.
Formulation of a priori indicators for sampling accuracy during the design phase is feasible and may be achieved by:
4.4.1 Target data populations
In the estimation of total catch and fishing effort (Sections 2 and 3), the two target data populations in sample-based catch/effort surveys are:
The target data population of fishing activity is used to formulate the probability (BAC) that any one boat would be fishing on any one day. The BAC will then be combined with the number of boats from a frame survey and a time raising factor to formulate an estimate for fishing effort.
The above two data populations have different sampling requirements for achieving the same level of accuracy. The next paragraph provides more detail on how sample size is determined in each case and in accordance with the level of accuracy desired.
The desired accuracy level for a sampling and estimation process depends on the subsequent use of the statistics and the amount of error that users are willing to tolerate. In general, experience indicates that the accuracy of basic fishery estimates should be in the range 90% - 95%.
The table below illustrates safe sample sizes required for achieving a given accuracy level for two target data populations, boat activities and landings.
|
Accuracy |
Sample size for boat activities |
Sample size for |
|
90 |
96 |
32 |
|
91 |
119 |
40 |
|
92 |
150 |
50 |
|
93 |
196 |
65 |
|
94 |
267 |
89 |
|
95 |
384 |
128 |
|
96 |
600 |
200 |
|
97 |
1,067 |
356 |
|
98 |
2,401 |
800 |
|
99 |
9,602 |
3,201 |
The above sampling requirements refer only to a given estimating context, that is a geographical stratum, a reference period (i.e. calendar month), and a specific boat/gear category. The process of determining safe sample size at a given level of accuracy must be repeated for all estimating contexts with the view to determining overall sampling requirements.
As already mentioned earlier, the second important statistical indicator is related to precision or, in reverse terms, to variability. The Coefficient of Variation (CV) is the most commonly used relative index of variability, usually expressed in percentage (i.e. 10%, 15%, etc). Experience indicates that CVs below 15% are indicators of acceptable variability in data samples. When very low variability (e.g. 0.1%, 0.5%) is repeatedly reported these results may be suspicious. Although this may indicate a very homogeneous data population, it may also be an indication of biased samples.
There are standard methods for explaining the overall variability in space and time. This is useful when it is feasible to increase sampling operations with the view to decreasing the variability of estimates. In such cases the availability of separate variability indicators in space and time would direct sampling operations to collect data from more locations or on more days. Reducing variability in estimates can also be addressed through the stratification of sampling (see below and section 5).
4.7.1 Definition
Stratification is the process of partitioning a target data population (e.g. all fishing vessels) into a number of more homogeneous sub-sets based on their characteristics (e.g. trawl, gillnet, purse seine; or large, medium, small; or commercial, artisanal, subsistence). Stratification is normally undertaken for the following reasons:
4.7.2 Impact on costs
The implementation of sampling stratification can be an expensive exercise and should always be applied with caution because all new strata need to be covered by the sampling programme. Introducing a large number of strata may have serious cost implications because the overall accuracy of the estimates will not be increased if data collection effort is kept at the original level, even though the results from strata will be more homogeneous than the original data population. In general, more strata means greater sampling costs, although obtaining better value (= statistical accuracy) for money.
To fully benefit from a stratified population, safe sample sizes must be determined for each new stratum. In very large populations this would mean that a new sampling scheme with three strata would need three times more samples for achieving the desired accuracy, hence greater costs.
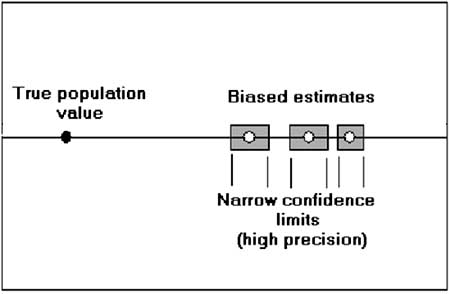
4.8.1 An illustrated example
The figure above illustrates in basic terms the problem of bias. Biased estimates may be found systematically above or below the true (but unknown) population value (here all estimates are shown higher than the true value). Bias is independent of the precision (= variability) of the estimates. In this example accuracy is bad but precision is misleadingly good and this is indicated by the narrow confidence limits.
4.8.2 Bias as a major risk in sampling programmes
Biased estimates are systematically lower or higher than the true population value, generally because they are derived from samples that are not representative of the data population. Bias is not easily detectable and at times not detectable at all. Consequently users may be unaware of the problem since they also do not know the true population value.
Precision (or the relative variability indicator CV) cannot be used to detect bias. However, repeated cases of extremely small variability (e.g. CV<1%) may be indications of a biased estimate.
Although attempts to increase the representativeness of samples are often compromised due to operational constraints, the best approach to the reduction of bias is through the application of appropriate stratification.
The risks of biased data are considerably reduced if sampling operations collect data that are as representative as possible.
4.9.1 Data collection at sampling sites
Collection of representative samples at a sampling site is not a difficult task provided that data collectors are adequately trained and briefed. For the collection of effort data, sampling should always be undertaken from a random selection of fishers without prior knowledge of whether they have been fishing or not.
When boats land within a short period, recorders at times tend to sample those with a small catch in order to cover as many landings as possible. Also, if landings occur over longer periods and recorders must visit other sites during the day, only the first landings at the first site will be sampled. These selections may introduce negative bias in CPUEs, species composition and prices. Therefore, care should always be taken to sample from a random selection of landings at random times.
4.9.2 Selection of sampling sites
In medium and large-scale fishery surveys the major task in obtaining representative samples is at the first sampling stage through selection of the locations where data will be collected. Often, a good approach is to select sampling sites on a rotational basis as part of an overall sampling strategy. Field teams would then cover the chosen sampling locations by visiting all of them at appropriate times, say once a month. Such an a priori selection of sampling sites enables planning for sufficient and mobile human resources.
When there are other operational constraints (accessibility, availability of data collectors, limited mobility, etc.), a planned rotational approach may not be feasible and data collection may be performed from sampling sites at fixed locations for long periods. The problem is that pre-selection of sampling sites runs the risk of biased samples if the landing sites are not representative of the entire statistical area.
4.9.3 Criteria for selecting sampling sites
Frame surveys and existing geographical information are used to make a priori selection of fixed sampling sites. The main criteria in selecting sampling sites are:
4.9.4 Example
Rather than examining sites on an individual basis, planners may look at groups of sites that offer a better statistical coverage because of their proximity. Criteria for grouping several sites together are:

The figure above illustrates a minor geographic stratum with 19 fishing sites. Table 4.9.5 contains the results of a frame survey for gillnets, beach seines and castnets.
Table 4.9.5 Frame survey data
|
Site |
Gillnets |
Beach seines |
Castnets |
|
1 |
4 |
0 |
7 |
|
2 |
11 |
0 |
0 |
|
3 |
1 |
8 |
2 |
|
4 |
5 |
0 |
9 |
|
Group 2, 3, 4 |
17 |
8 |
11 |
|
5 |
12 |
4 |
5 |
|
6 |
3 |
0 |
0 |
|
7 |
2 |
1 |
3 |
|
8 |
2 |
2 |
0 |
|
9 |
4 |
1 |
0 |
|
10 |
5 |
3 |
6 |
|
11 |
4 |
3 |
0 |
|
12 |
3 |
2 |
4 |
|
13 |
1 |
0 |
9 |
|
14 |
0 |
0 |
7 |
|
15 |
8 |
3 |
6 |
|
16 |
7 |
4 |
3 |
|
Group 13, 14, 15, 16 |
16 |
7 |
25 |
|
17 |
6 |
0 |
0 |
|
18 |
14 |
5 |
9 |
|
19 |
5 |
0 |
7 |
the second option offers more statistical advantages both for in-space coverage and boat/gear representativeness.
Determining the fishing unit (boat or gear) that will be the subject of sampling operations is a major decision in planning sample-based fishery surveys.
4.10.1 The “boat” approach
The fishing boat as statistical unit is the commonest approach because:
4.10.2 The “gear” approach
Alternatively the fishing gear type can be used as the statistical unit, e.g. 100-metre gillnet units, 500-hook line units, 100-metre beach seine units or traps, etc. This approach can be used when:
4.10.3 Comparison of the two approaches
Overall, the “boat-specific” approach is more advantageous than the “gear-specific” because:
The major advantage of the “gear” approach is that it can better handle cases of multiple gears (whether in sequential or concurrent use).
|
SUMMARY In this section general aspects of sampling methods have been discussed, including: (a) The reason for and objectives of sampling: sampling techniques can provide estimates of good reliability and are more economical than census approaches. |