5.1 Función producción en el corto plazo
5.2 Rendimientos de escala
5.3 Funciones de costos
5.4 Curva de costo promedio en el largo plazo
5.5 Microeconomía aplicada a pesquerías
La función producción surge dentro del análisis microeconómico como uno de los dos elementos determinantes de la sustentabilidad de la empresa. Un empresario que intenta alcanzar una situación de equilibrio de la empresa, es decir, que intenta maximizar su beneficio a corto plazo, debe tener en cuenta simultáneamente las características tecnológicas de sus instalaciones y las posibilidades de utilización de las mismas que le brindan las técnicas productivas existentes. Además, debe considerar el costo del proceso productivo.
El primero de estos elementos está representado formalmente por una función producción. En un país dado, existe una técnica productiva determinada, materializada en las instalaciones existentes en los distintos sectores productivos, en los procedimientos concretos de producción, en distintas formas de organización, de gestión empresarial, de división del trabajo. Esta situación puede representarse funcionalmente por medio de una relación que ligue el valor agregado en el curso de la producción o el producto nacional con las cantidades aplicadas de los distintos factores productivos. Estos conceptos conforman la función agregada de producción para cada sector, por ejemplo, la función agregada de las plantas de congelado de pescado.
Disponer de la función producción de cada sector de la industria pesquera permitiría evaluar la respuesta ante cambios que puedan producirse en el futuro como: disminución de la mano de obra, escasez de una determinada especie, innovación tecnológica. Más aún, puede determinarse hasta qué punto es posible realizar sustitución de un insumo por otro. Asimismo, puede evaluarse el rango de utilización de la planta que corresponde a la máxima eficiencia de producción.
Además, la función agregada de producción puede ser utilizada como instrumento para comparar los problemas de eficiencia productiva internacional y de estructura de precios relativos de los productos de distintos países. Este capítulo presenta varias propiedades del proceso productivo de una empresa e introduce algunos de los factores que gobiernan la elección de tecnologías de producción. Específicamente, se considerará el tipo de proceso productivo y las propiedades de la función producción de la empresa.
Asimismo, debe considerarse el rol de la tecnología y los avances tecnológicos para alterar la capacidad de la empresa para producir bienes y servicios, y la presión sobre las empresas para adoptar nuevas tecnologías.
La producción es una serie de actividades por las cuales los insumos o recursos utilizados (materia prima, mano de obra, capital, tierra y talento empresario) son transformados en un determinado período de tiempo en productos (bienes o servicios). Los economistas usan el término función producción para referirse a la relación física entre los insumos utilizados por la empresa y sus productos (bienes o servicios) por unidad de tiempo (Henderson y Quandt, 1971). Esta relación puede expresarse simbólicamente:
Q = f (Xa, Xb, Xc, ......, Xn) .......... (5.1)
donde Xa, Xb, Xc, ...., Xn representan cantidades de distintos tipos de insumos y Q representa la cantidad de producto total por período de tiempo a partir de combinaciones específicas de estos insumos. Existe una función producción para cada tecnología. Una empresa puede modificar las cantidades de producto variando las cantidades de recursos que combina de acuerdo con una técnica productiva, cambiando de una tecnología a otra o empleando ambas acciones. Se supone que la empresa emplea la técnica más eficiente, de tal manera que obtiene la máxima producción de cada combinación alternativa de insumos.
En el tratamiento microeconómico de la función producción se definen los siguientes parámetros, que son de interés para este análisis:
Un insumo fijo (IF) se define como aquél cuya cantidad no puede rápidamente ser cambiada en el corto plazo, como respuesta a un deseo de la empresa de cambiar su producción. Realmente, los insumos no son verdaderamente fijos en un sentido absoluto, aún en el corto plazo. Prácticamente, sin embargo, el costo de efectuar variaciones en un insumo fijo puede ser prohibitivo. Ejemplos de insumos fijos: piezas de equipos o maquinarias, espacio disponible para la producción, personal directivo, etc.
Por el contrario, insumos variables (IV) son aquéllos que se pueden alterar muy fácilmente en cantidad como respuesta al deseo de elevar o disminuir el nivel de producción. Por ejemplo, energía eléctrica, materias primas, mano de obra directa, etc. A veces, los insumos variables están limitados en su variación debido a contratos (por ej., oferta fija de materia prima) o leyes (por ej., leyes laborales); en dichos casos es posible hablar de insumos semi-variables (ISV).
El corto plazo (CP) es el período de tiempo en que la empresa no puede variar sus insumos fijos. Sin embargo, el corto plazo es adecuadamente largo como para permitir la variación de los insumos variables. El largo plazo (LP) se define como el período de tiempo suficientemente largo como para permitir la variación de todos los insumos; ningún insumo está fijo, incluyendo tecnología. Por ejemplo, mientras en el corto plazo una empresa puede aumentar su producción trabajando horas extras, en el largo plazo la empresa puede resolver construir y expandir su superficie de producción para instalar maquinarias capital-intensivas y evitar sobreturnos.
La cantidad de insumos fijos de una planta es factor determinante de la escala de operaciones. La escala de una planta determina a su vez el límite máximo de producto por unidad de tiempo, que esa empresa es capaz de producir en el corto plazo. La producción puede ser variada, en el corto plazo, disminuyendo o aumentando el uso de insumos variables en relación con la cantidad de insumos fijos. En el largo plazo, la producción puede ser aumentada o disminuida cambiando la escala de producción, la tecnología utilizada y el uso de todos o cualquiera de los insumos. Para analizar la función producción en el corto plazo, es necesario además, definir los siguientes conceptos:
El producto promedio (PP) que es la producción total por unidad de insumo utilizado y el producto marginal (PM) que es el cambio en la cantidad producida por unidad de tiempo resultante de un cambio unitario en la cantidad del insumo variable. La forma de las curvas de PP y PM se determinan por la forma de la correspondiente función producción (PT).
El principio de los rendimientos marginales decrecientes, se relaciona con las cantidades de producto que pueden obtenerse, cuando crecientes cantidades de insumos variables por unidad de tiempo son incorporados al proceso productivo y combinadas con una cantidad constante de insumo fijo. El principio establece que se encontrará un punto donde los incrementos de producto obtenidos resultan cada vez menores. Cuando el producto promedio está aumentando, el producto marginal es mayor que el promedio; cuando el promedio alcanza su máximo, éste iguala al producto marginal.
Antes de alcanzar el inevitable punto de rendimientos marginales decrecientes la cantidad de producto final obtenida puede aumentar a una velocidad creciente como se observa en la Figura 5.1. Por encima del punto de inflexión de la función producción, un mayor uso del insumo variable provoca una disminución del producto marginal. Una función producción y las curvas de PP y PM asociadas pueden dividirse en 3 etapas, como se ilustra en la Figura 5.1.
La etapa 1 se extiende desde cero unidades de insumos variables (IV) hasta el punto donde el PPIV es máximo (Punto de Retornos Promedios Decrecientes, RPD). La etapa 2 se extiende desde el máximo de PP hasta el punto donde la cantidad de producto es máximo y el PM es cero (Punto de Retornos Totales Decrecientes, RTD). La etapa 3 coincide con el rango de IV, donde el producto total está disminuyendo y el PM es negativo.
Las etapas tienen un significado especial para analizar la eficiencia con la que son utilizados los recursos. El máximo de (PM) vs (unidades de IV) define el punto de RMD a partir del cual un aumento en los IV significarán una disminución en el (PM). La primera etapa corresponde al rango en el cual el PP está aumentando como resultado de la utilización de cantidades crecientes de insumos variables (materia prima, mano de obra, etc.).
Un productor racional no operaría en este rango debido a que los insumos fijos, (IF) (equipos) están siendo subutilizados. Esto es, la producción esperada por la utilización de más horas-hombre, por ejemplo, está aumentando a través de la etapa 1, lo que indica que la misma producción podría ser obtenida con una cantidad menor de insumo fijo. En la etapa 3 tampoco es conveniente la producción. Unidades adicionales de IV realmente reducen la producción total.
Si la eficiencia del proceso productivo es medida por el producto promedio ya que el mismo indica la cantidad de producto obtenida por unidad de insumo, la discusión anterior pone de manifiesto que la etapa 2 es la mejor desde el punto de vista de la eficiencia. En la etapa 1, los (IV) están siendo usados en muy pequeña proporción comparados con los (IF). Las consideraciones de eficiencia llevarán a la empresa a producir, por lo menos, en el límite de las etapas 1 y 2.
Se ha analizado la función producción de la empresa en el corto plazo, donde una porción de los recursos de la misma son fijos. El concepto de rendimientos de escala aparece cuando la empresa está en producción durante un período de tiempo lo suficientemente largo como para permitir cambios en cualesquiera y todos sus insumos, en especial, aquéllos que son típicamente fijos en el corto plazo.
Los rendimientos de escala se definen para el caso en que todos los insumos son cambiados en iguales proporciones. Si se considera una empresa que utilizando X1 unidades de mano de obra en combinación con X2 unidades de capital, obtiene Q unidades de producto, podemos escribir:
X1 + X2 ® Q .......... (5.2)
Ahora suponemos, que las cantidades de X1 y X2 son variadas en una proporción arbitraria ¶ . Obviamente, la producción total cambiará; la pregunta es en qué proporción lo hará. Si se designa esta proporción como tendremos:
¶ X1 + ¶ X2 ® p Q .......... (5.3)
1. Si el cambio en la producción es más que proporcional al cambio en los insumos (p > ¶), se dice que existen rendimientos crecientes de escala.
2. Si p = ¶ se dice que existen rendimientos constantes de escala.
3. Si p < ¶, se dice que existen rendimientos decrecientes de escala.
Para una misma tecnología es generalmente cierto que al expandir la escala de la operación, la empresa pasará sucesivamente por:
1. Un período corto de rendimientos crecientes de escala.
2. Un largo período de rendimientos constantes, y
3. Un período de rendimientos decrecientes.
Por lo tanto, una empresa puede incrementar el uso de sus insumos hasta el punto de máxima producción; aumentos posteriores de insumos podrían producir una etapa de rendimientos negativos donde la producción realmente disminuye. Sin embargo, si el concepto de rendimientos de escala es utilizado para permitir cambios en la capacidad técnica de la firma, y su tamaño aumenta, las empresas pueden ser (y ciertamente lo son) capaces de aplicar todas sus herramientas y nuevas tecnologías para expandir su escala de operaciones sin encontrar nunca el punto de rendimientos decrecientes.
Las empresas con un prolongado período de rendimientos constantes son las más observadas en los casos reales de plantas productoras de alimentos y plantas pesqueras.
5.3.1 Costos totales y costos unitarios
5.3.2 Las curvas de costos en el corto plazo en la industria pesquera
Un punto fundamental en el análisis de costos es la relación funcional que existe entre los costos y la producción por período de tiempo. Una función de costos presenta distintos resultados cuando la planta trabaja con diferentes porcentajes de utilización. Pero, como se indicó anteriormente, la producción es una función del modo en que se utilicen los recursos.
De manera tal, que como la función producción establece la relación entre insumos y producto, una vez que los precios de los insumos son conocidos, los costos para una determinada producción pueden ser calculados. Como consecuencia, el nivel y comportamiento de los costos de una planta, a medida que varía el nivel de producción, está directamente relacionado con:
1. Las características de su propia función producción.
2. Los precios de compra de sus insumos.
Tres conceptos de costos totales son importantes para analizar la estructura de costos en el corto plazo: costo fijo total, costo variable total y costo total.
Los costos fijos totales (CFT) pueden definirse como la suma total de los costos de todos los insumos fijos asociados con la producción. Como los insumos fijos de una empresa no pueden ser cambiados en el corto plazo, los CFT son constantes salvo que los precios de los insumos fijos cambien (mayores impuestos a la propiedad, aumentos en las tasas de los seguros, etc.). Más aún, CFT continúan existiendo aunque la producción se vea detenida.
En forma similar, los costos variables totales (CVT) representan la suma de todas las cantidades de dinero que la empresa gasta en insumos variables empleados en la producción.
Como en el corto plazo la empresa modifica su nivel de producción, los costos variables dependen de la cantidad producida. El CVT es cero cuando la producción es cero ya que en ese momento no son necesarios los insumos variables. Luego:
CT = CFT + CVT .......... (5.4)
Esta expresión indica que el costo total para una dada producción en el corto plazo, es la suma del costo fijo total y el costo variable total. Asimismo, son de interés los siguientes cuatro costos unitarios: costo fijo promedio (CFP), costo variable promedio (CVP), costo total promedio (CTP) y el costo marginal (CM). El costo fijo promedio está definido por el cociente entre el costo fijo total y las unidades de producción:
CFP = CFT/Q .......... (5.5)
Como el costo fijo total es constante, el costo fijo promedio disminuye a medida que aumenta la producción, es decir, se distribuyen los mismos costos fijos entre más unidades producidas. También puede calcularse el CFP del siguiente modo: el CFT es el producto del número de unidades de insumos fijos (IF) por el precio de esos insumos (PIF). Substituyendo en la expresión 5.5:
CFP = CFT/Q = (PIF) × (IF)/Q = PIF × (IF/Q) .......... (5.6)
Recordando que se ha definido el producto promedio de los insumos fijos como la cantidad total producida (Q) dividido el número de unidades de insumos fijos (IF), se ve que IF/Q es la inversa del PPIF
CFP = PIF × (1/PPIF) .......... (5.7)
El costo variable promedio es el CVT dividido el correspondiente número de unidades producidas, o:
CVP = CVT/Q .......... (5.8)
Similarmente, el CVP puede expresarse en función de la inversa del PPIV
CVP = CVT/Q = PIV × (IV/Q) = PIV × (1/PPIV) .......... (5.9)
El costo total promedio está definido por el costo total dividido el número de unidades de Q correspondientes:
CTP = CT/Q .......... (5.10)
Sin embargo, por ecuación 5.4:
CTP = CT/Q = (CFT + CVT)/Q = CFT/Q + CVT/Q = CFP + CVP
Por último, el costo marginal es el cambio en el costo total asociado con el cambio en la cantidad de producto por unidad de tiempo. Como antes, podemos hacer una distinción entre costo marginal discreto y continuo.
El costo marginal discreto es el cambio en el costo total atribuible a un cambio de 1 unidad en la cantidad de producto. Costo marginal continuo es la velocidad de cambio en el costo total a medida que la producción varía, y puede ser calculado como la derivada primera de la función de costo total.
CM = dCT/dQ (costo marginal continuo) .......... (5.11)
Sin embargo, dado que en el corto plazo la variación en la producción sólo puede ser atribuida a la variación en Los insumos variables, es equivalente a medir la variación en el costo marginal discreto por la variación observada en el costo total o en el costo variable total. Luego:
CM = dCVT/dQ (costo marginal continuo en el corto plazo) .......... (5.12)
También el CM está relacionado con la función producción. Dado que los cambios en la producción en el corto plazo se producen por aumento o disminución de los (IV), los cambios en el CVT (D CVT) pueden ser calculados multiplicando el precio del insumo variable (PIV) por el cambio producido en el insumo variable (D IV), dando:
D CVT = PIV × (D IV) .......... (5.13)
Reemplazando en 5.12 y por la definición de producto marginal:
CM = PIV × (1/PM) .......... (5.14)
El costo marginal es de interés fundamental ya que refleja aquellos costos sobre los que la empresa tiene el control más directo en el corto plazo. Indica la cantidad del costo que no debe ser gastada al reducir la producción en una unidad o, alternativamente, la cantidad de costo adicional en que se incurrirá al aumentar la producción en una unidad.
Los datos de costos promedio no revelan este conocimiento tan valioso. Se aplican todos estos conceptos para analizar el comportamiento de las empresas con sus diferentes funciones de producción. Aquí sólo se examinarán las funciones de costo total, promedio y marginal para la función de producción en el corto plazo con rendimientos crecientes y decrecientes a los insumos variables, cuya expresión matemática es:
Q = a + b × (IV) + c × (IV)2 - d × (IV)3 .......... (5.15)
donde Q es la cantidad de producto e (IV) las unidades de insumo variable; a, b, c, y d son constantes. Los resultados se muestran en la Figura 5.2, pudiéndose observar la forma "S" característica de la curva de costos totales.
Un estudio de aplicación de estos criterios a plantas de alimentos (Figura 5.3) mostró una respuesta no lineal para curvas de costos semivariables en el corto plazo (Zugarramurdi y Parin, 1987b).
Los costos semi-variables (CSVT) se definen como los costos variables que no son directamente proporcionales a la producción como los servicios administrativos, mantenimiento y supervisión.
El conocimiento de la estructura de costos de la planta funcionando a plena capacidad permite realizar fácilmente una estimación del costo que se tendría al operar la planta a niveles inferiores. En la Tabla 5.1 se han calculado para diferentes estructuras de costos la relación del costo de producción unitario de la planta operando a una cierta capacidad con respecto al costo de la misma planta a plena capacidad. En la parte inferior de la Tabla 5.1 se dan valores para los casos especiales de plantas pesqueras, de acuerdo a las estructuras de costos de la Tabla 4.16 (Capítulo 4).
Se observa claramente que las plantas pesqueras muestran una alta incidencia de los costos variables. Específicamente, son materia prima y mano de obra intensivas. Este tratamiento simplificado, linealiza la variación de todos los costos variables y semivariables con la utilización de la planta, aunque, como se demostró anteriormente, los costos semivariables no varían linealmente con la producción en el corto plazo. Sin embargo, la baja proporción de estos costos sobre los costos totales permite realizar esta aproximación (Zugarramurdi, 1981a).
Tabla 5.1 Costos de producción en función del porcentaje de capacidad operada
|
Estructura % del costo anual al 100% de la capacidad |
Relación de costo unitario a la capacidad indicada con respecto al costo unitario a plena capacidad |
||||||
|
Planta Tipo |
Variables |
Fijos |
% Capacidad operada |
||||
|
20 |
40 |
60 |
80 |
100 |
|||
|
A |
90 |
10 |
1,40 |
1,15 |
1,07 |
1,03 |
1,00 |
|
B |
80 |
20 |
1,80 |
1,30 |
1,13 |
1,05 |
1,00 |
|
C |
70 |
30 |
2,20 |
1,45 |
1,20 |
1,08 |
1,00 |
|
D |
60 |
40 |
2,60 |
1,60 |
1,27 |
1,11 |
1,00 |
|
E |
50 |
50 |
3,00 |
1,75 |
1,34 |
1,14 |
1,00 |
|
F |
40 |
60 |
3,40 |
1,90 |
1,41 |
1,17 |
1,00 |
|
G |
30 |
70 |
3,80 |
2,05 |
1,48 |
1,20 |
1,00 |
|
H |
20 |
80 |
4,20 |
2,20 |
1,56 |
1,23 |
1,00 |
|
I |
10 |
90 |
4,60 |
2,35 |
1,63 |
1,26 |
1,00 |
|
Plantas Pesqueras |
|
||||||
|
Conservas |
78,0 |
22,0 |
1,89 |
1,33 |
1,15 |
1,06 |
1,00 |
|
Salado |
81,5 |
18,5 |
1,74 |
1,28 |
1,12 |
1,05 |
1,00 |
|
Congelado |
82,0 |
18,0 |
1,72 |
1,27 |
1,12 |
1,04 |
1,00 |
|
Harina |
86,0 |
14,0 |
1,56 |
1,21 |
1,09 |
1,03 |
1,00 |
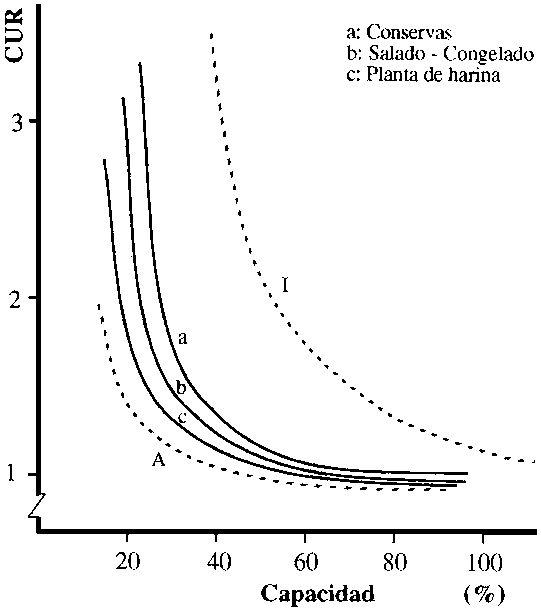
Los valores se muestran en la Figura 5.4, en la cual se han graneado las curvas límites correspondientes a una estructura de costos A e I, en línea punteada y con trazo lleno las curvas correspondientes a plantas pesqueras.
Figura 5.4 Variación del costo unitario relativo (CUR) para diferentes niveles de producción en plantas pesqueras (Estructura de costos A-I definida en la Tabla 5.1)
5.4.1 Las curvas de costos en el largo plazo para plantas reales
Debido a que en el largo plazo no existen más insumos fijos, desaparece la distinción entre insumos variables y fijos y no hay curvas de CFT o CVT. En realidad, sólo se hace necesario mirar la naturaleza de la forma de la curva de costos promedios en el largo plazo. Supóngase que las restricciones tecnológicas permiten a una empresa elegir entre la construcción de tres plantas de tamaños diferentes: pequeño, mediano y grande. Las porciones de las 3 curvas de costos promedio en el CP que identifican el tamaño óptimo de planta para una producción dada se observan en trazo sólido en la Figura 5.5.
Figura 5.5 Curva de costo total promedio (CTP) en el largo plazo para plantas de tres distintos tamaños
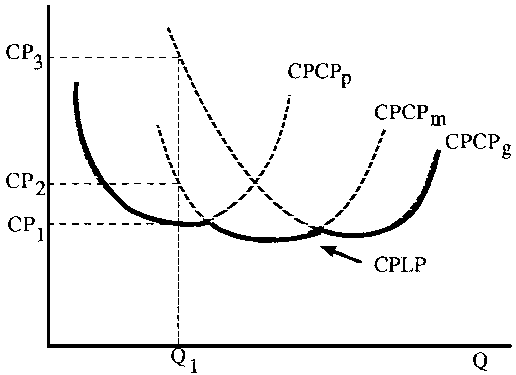
Esta línea es llamada la curva de costo promedio en el largo plazo (CPLP) y muestra el costo unitario mínimo para cualquier producción cuando todos los insumos son variables y es posible construir todo tamaño de planta. Las líneas punteadas de las curvas de CPCP corresponden siempre a costos mayores a cada producción de los que es posible obtener con plantas de otros tamaños.
Obviamente, la elección final dependerá de la demanda del mercado y las tendencias de las demandas del consumidor, favoreciendo en general las plantas de mayor tamaño en los planteos futuros. De otra manera, la planta mediana resultará la más atractiva, debido a sus menores requerimientos de inversión. Usualmente la firma tendrá más de 3 tamaños para elegir. Cuando este número tiende a infinito, la curva de CPLP encierra las curvas de CP y es tangente a ellas, como se observa en la Figura 5.6.
Figura 5.6 Curva de costo promedio en el largo plazo para plantas de cualquier tamaño
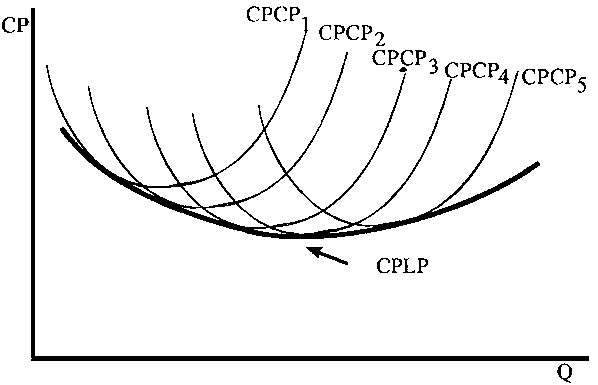
De todas las plantas posibles, aquélla cuya curva de CPCP es tangente a la curva de CPLP en el punto mínimo es la más eficiente. En la Figura 5.6, la planta de tamaño óptimo corresponde a la curva de CPCP4.
Se enumerarán las razones principales de las distintas formas de las curvas de CPLP y cómo se relacionan con la capacidad de la planta. La primera posibilidad para analizar es la de industrias donde los CP decrecen proporcionalmente con Q. Se observa que a mayor volumen de producción se genera una mayor subdivisión del proceso productivo y una especialización en la utilización de insumos como materia prima, mano de obra y supervisión.
Esto tiene como consecuencia directa un incremento de eficiencia y una reducción de costos. Asimismo, las grandes plantas tienen la posibilidad de obtener por el volumen de negocios, descuentos amplios en los precios de las materias primas y ofrecer a sus clientes mejores condiciones de ventas, logrando una penetración en el mercado.
A su vez, también a nivel organización empresarial tienen ventajas, pues el personal administrativo y gerencial es compartido entre las distintas unidades de producción. La gran empresa, ya sea por vía vertical o por diversificación puede afrontar los cambios en el mercado por aumentos bruscos de precios, escasez de materias primas o innovaciones tecnológicas. Estas economías de escala son extremadamente importantes y determinan que la curva de CPLP disminuya para el rango de grandes producciones. Ejemplos: plantas de automotores, aluminio, acero, papel, aviación, maquinarias para el agro. En las plantas de alimentos, tienen este comportamiento algunas plantas de conservas de vegetales, de jugos y de conservas de pescado (Figura 5.7).
Sin embargo, en algunas industrias, se producen inconvenientes al crecer su tamaño. Esto se debe a que se producen diseconomías de escala por las dificultades crecientes en el nivel gerencial que insumen tiempos y costos mayores y problemas relacionados con los insumos y su complementación.
La Figura 5.8 muestra una curva de CPLP para estas empresas cuando las diseconomías suceden a niveles bajos de producción. Ejemplos: agricultura, imprentas, panaderías, electrónica, instrumental, embotelladoras de bebidas sin alcohol. Los ejemplos encontrados en el sector de alimentos donde la planta de menor escala tiene ventajas de costos sobre las de mayor escala, incluyen el procesamiento de vegetales congelados.
Figura 5.8 Curva de costos promedio en el largo plazo, para el caso de diseconomías tempranas
La Figura 5.9 presenta una curva de CPLP que tiene forma de U con fondo plano, lo que implica rendimientos constantes de escala sobre un amplio rango de capacidades. Ejemplos: empaque de carnes, dispositivos para el hogar, muebles, textiles, alimentos, industrias químicas.
Figura 5.9 Curva de costos promedio en el largo plazo, para el caso de costos promedio constantes
Ejemplo 5.1 Costos de producción en el corto y largo plazo para plantas artesanales de harina de pescado
Calcular y comparar los costos de producción en el corto y largo plazo para plantas de harina de pescado: plantas artesanales de Africa y plantas de gran escala en Europa.
Una planta de tamaño pequeño está operando en Africa, con una capacidad de sólo 100 kilos de materia prima/día (con un rendimiento del 20%). Esta planta emplea una tecnología simple, a fin de adaptarse a las características de la villa en la que está emplazada. La cocción se realiza bajo techo y el secado al sol (Mlay y Mkwizu, 1982). Por otra parte, las plantas a gran escala están funcionando en países desarrollados de Europa, trabajando eficientemente para grandes capacidades, con tecnologías que incluyen plantas de concentrado de agua de cola (Atlas, 1975).
Solución:
En general, cuando se analizan los costos de producción, el concepto de economía de escala parecería indicar que la planta de mayor producción es la más adecuada. Sin embargo, algunos estudios económicos (Cerbini y Zugarramurdi, 1981b) demuestran que en ciertos casos, ni aún el mercado total atendido por una sola fábrica en países en desarrollo alcanzaría a asegurar la productividad con que se opera normalmente en los países más industrializados.
Estas circunstancias indican la existencia de un problema técnico especial, en los países en vías de desarrollo, que consiste en aplicar procesos que permitan mejorar la productividad en operaciones de menor escala.
La aplicación de los procedimientos considerados clásicos en los países desarrollados conduce a costos de operación excesivos en países de mercado pequeño.
En la Figura 5.10 se muestran los costos en el corto y largo plazo para ambas economías.
Puede verse claramente, que el uso de la tecnología apropiada a cada país o región permite obtener los menores costos de producción y un aprovechamiento eficiente de los insumos locales. Los costos de operación muestran un comportamiento de acuerdo con el concepto de economía de escala.
Plantas artesanales son posibles de instalar con la tecnología adecuada para el país correspondiente, de acuerdo con las disponibilidades de insumos, obteniéndose costos de producción considerablemente menores. También debe mencionarse que existen razones técnicas y económicas que no hacen viable estas alternativas cuando la capacidad aumenta.
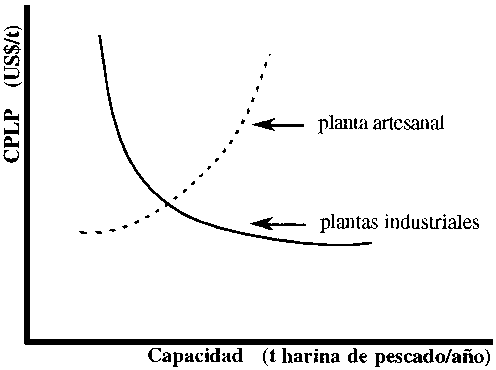
Por ejemplo, los costos de mano de obra se incrementan exponencialmente cuando se deben procesar grandes volúmenes como es el caso de secado natural. El control de insectos no es posible de realizar eficientemente y se pierde materia prima con el consiguiente aumento del costo total de producción. Con la cuantificación de todos estos factores la curva real de costos para plantas artesanales tomaría una forma del tipo de la graficada en línea punteada en la Figura 5.11.
En esta situación, ambos tipos de producción - artesanal e industrial - podrían coexistir, como en el caso de Tanzania con la producción de harina de pescado a partir de Haplochromis spp. en Lago Victoria en los 1970's y 1980's (la producción industrial de harina de pescado cesó cuando las pesquerías de Haplochromis colapsaron luego de la introducción de la pesca del Nilo en el Lago Victoria).
Figura 5.11 Curva de costos promedio en el largo plazo para plantas artesanales e industriales de harina de pescado
Ejemplo 5.2 Análisis de las curvas de costos promedios en el largo plazo para embarcaciones pesqueras en Africa Occidental
Analizar las economías de escala en embarcaciones pequeñas de la costa oeste de Africa: (a) Ghana; (b) Costa de Marfil; y (c) Senegal, de acuerdo con los datos publicados por Frielink, 1987.
(a) Ghana. Las pesquerías de sardinela (Sardinella spp).
Se utilizan 2 tipos de embarcaciones para la explotación de sardinela en esa región: unas son menores de 12 metros de largo y otras miden entre 12 y 22 metros. Se estudiaron 32 embarcaciones que representan aproximadamente el 10% de la flota total registrada en 1983. Se las clasificó en 3 grupos de diferente tamaño: 0 a 9,9 m, 10,0 a 18,3 m y 18,4 a 30,5 m, con 7,14 y 11 embarcaciones respectivamente. Analizar los costos de captura para cada grupo, consignados en la Tabla 5.2. Los costos variables son aproximadamente el 75% del costo total, resultado que se aplica a muchas otras pesquerías. El combustible representa alrededor del 30% del costo total.
Tabla 5.2 Captura, ingresos, costos y rentabilidad de embarcaciones en Ghana
|
Embarcaciones |
Pequeñas (A) |
Medianas (B) |
Grandes (C) |
|
Captura (t/año) |
178 |
208 |
236 |
|
Ingresos brutos (US$/año) |
33 820 |
39 520 |
44 840 |
|
Inversión (US$) |
47 150 |
58 720 |
65 675 |
|
Costos totales (US$/año) |
29 455 |
34 742 |
41 546 |
|
Costo promedio (US$/t) |
165 |
167 |
176 |
|
Tasa de retorno (%) |
5,67 |
4,77 |
1,6 |
Solución: Se observa que las embarcaciones de mayor tamaño (C) son las menos rentables. Los ingresos brutos superiores en un 13,5% de las embarcaciones (C) en comparación con las embarcaciones (B) no compensa el incremento en un 19,6% en los costos de producción.
Los valores de costos promedio se han graficado en la Figura 5.12 donde se observa la presencia de diseconomías tempranas.
La diferencia entre el tamaño (A) y el (B) no es grande en términos de rentabilidad, pero el tamaño medio de la embarcación es probablemente una mejor inversión debido a que puede suponerse que tendrá más posibilidades y un rango más amplio de acción (Frielink, 1987).
Figura 5.12 Curva de costos promedio en el largo plazo para embarcaciones de Ghana
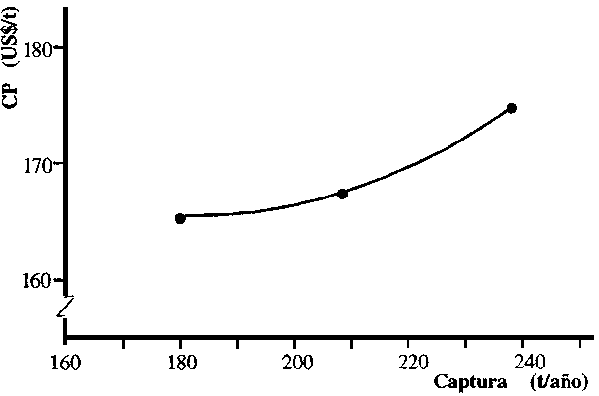
(b) Costa de Marfil. La pesquería de sardinela en Abidjan.
Dieciséis embarcaciones entre 18,4 y 28,8 m de eslora operaban en Costa de Marfil en 1983. Se trata de embarcaciones de madera construidas en Abidjan, con motor y sin sistema de refrigeración. Para el estudio se han dividido en 2 categorías: las pequeñas, con motor de 240 hp promedio, y las grandes con motores de 450 hp.
Debido a que el comportamiento de las embarcaciones individuales en cada grupo mostraban grandes diferencias, se seleccionaron valores promedio en lugar de utilizar embarcaciones típicas. En 1983, el número total de viajes fue de 110 y 122, respectivamente, con capturas totales de 1 425 y 1 723 toneladas. En la Tabla 5.3 se muestran los costos y beneficios de la pesquería.
Tabla 5.3 Captura, ingresos, costos y rentabilidad de embarcaciones en Costa de Marfil
|
|
Embarcaciones pequeñas |
Embarcaciones grandes |
|
Captura (t/año) |
1 425 |
1 723 |
|
Ingresos brutos (US$/año) |
422 716 |
513 853 |
|
Costos promedio (US$/t) |
229,5 |
256,2 |
|
Tasa de retorno (%) |
15,8 |
7,4 |
Solución: En la Figura 5.13 se han representado los costos promedio, resultando similar al caso anterior, diseconomías tempranas, dado que el beneficio es un 35% menor para las embarcaciones grandes.
Al igual que en otras pesquerías, los costos variables insumen aproximadamente las tres cuartas partes del costo total. No existen grandes diferencias en la estructura de costos de ambas clases de embarcaciones, con excepción de combustibles y lubricantes e intereses. En las embarcaciones grandes los costos de combustibles son relativamente superiores y, debido a la mayor inversión, deben soportar pagos de intereses sustancialmente más altos.
Históricamente, los costos de embarcaciones grandes son casi el doble que las de embarcaciones menores. La producción y los ingresos por pescador son 10% menores para las embarcaciones mayores, indicando la disminución en la productividad con el aumento de potencia del motor que es común a esta actividad. Además, el valor agregado por embarcación es más alto para las embarcaciones mayores, principalmente debido a los altos intereses pagados. La tasa de retorno es aceptable para las embarcaciones pequeñas, y mayor que la tasa bancaria. Esto también es cierto para las embarcaciones mayores, aunque el 7,4% es demasiado bajo para el riesgo involucrado en la actividad (Frielink, 1987).
Figura 5.13 Curva de costos promedios en el largo plazo para embarcaciones de la Costa de Marfil
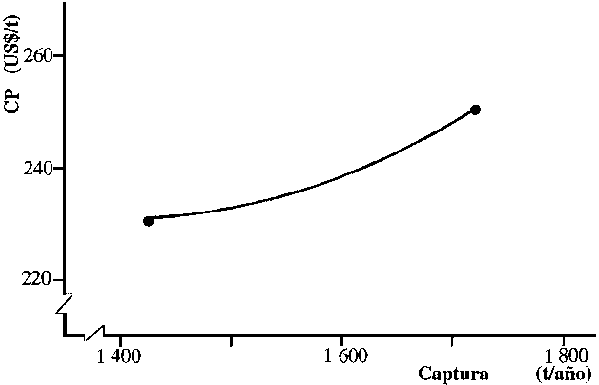
(c) Senegal. La pesquería de pequeños pelágicos en Dakar.
Los cerqueros de la flota de Dakar están compuestos por diferentes tipos y tamaños de embarcaciones. Los tamaños varían desde 22 hasta 256 toneladas de registro bruto, con motores de 110 hasta 600 hp. Las embarcaciones antiguas son de madera y las más nuevas de fibra de vidrio. En la Tabla 5.4, se muestra la composición de la flota agrupadas las embarcaciones en cuatro clases.
Tabla 5. 4 Características de la flota de cerqueros de Dakar (Senegal)
|
Clase |
Material de construcción |
Captura 1983 (t) |
Captura por viaje (t) |
Número de viajes por año |
Tripulantes |
Inversión (US$) |
|
C1 |
Fibra de vidrio |
392 |
3 |
140 |
10 |
157 450 |
|
C2 |
Fibra de vidrio |
1 370 |
5,5 |
249 |
16 |
289 000 |
|
C3 |
Madera |
1 159 |
6,1 |
190 |
20 |
525 000 |
|
C4 |
Madera/Acero |
2 200 |
11,0 |
200 |
24 |
630 000 |
En la Tabla 5.5 se muestran los costos e ingresos de los cuatro tipos de embarcaciones para el año 1983.
Tabla 5.5 Captura, ingresos, costos y rentabilidad de embarcaciones en Senegal
|
Tipo de embarcación |
C1 |
C2 |
C3 |
C4 |
|
Captura (t/año) |
392 |
1 370 |
1 159 |
2 200 |
|
Ingresos brutos (US$/año) |
55 559 |
194 173 |
164 268 |
311 811 |
|
Costos promedio (US$/t) |
169,4 |
117,0 |
188,6 |
141,9 |
|
Tasa de retorno (%) |
- |
8,4 |
- |
- |
Solución: La estructura de costos es algo diferente de las otras pesquerías. Los costos totales variables son menores del 75% del costo total. La principal razón es que el esfuerzo de pesca es inusualmente bajo. Las embarcaciones deben operar 250 a 280 días por año. Además, debido a los viajes cortos, el costo de combustible como porcentaje del costo total representa del 11 al 18%, en lugar del 25-30% observado en otras pesquerías. Los salarios resultan relativamente altos, debido a que parte de los mismos son fijos. Del análisis de la Tabla 5.5, sólo las embarcaciones C2 operaron en forma rentable en 1983, las otras reportaron pérdidas que fueron importantes como en el caso de las C3.
La principal razón para la alta rentabilidad de las C2 en relación con los otros tipos de embarcaciones parece ser el número de viajes. Las C4 mostraron pérdidas a pesar de sus altas capturas, probablemente debido a sus grandes costos de depreciación. En la Figura 5.14 se han representado los costos promedios para las cuatro clases de embarcaciones, observándose que las embarcaciones intermedias de fibra de vidrio resultan más convenientes.
Figura 5.14 Curvas de costos promedio en el largo plazo para embarcaciones de Senegal
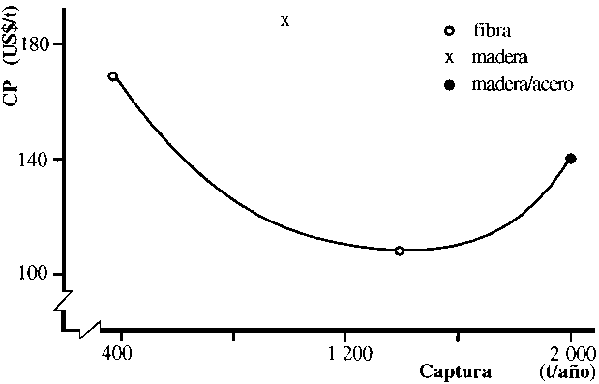
Ejemplo 5.3 Análisis de las economías de escala en la producción de harina y aceite de pescado en el Sultanato de Omán (Arnesen and Schärfe, 1986)
En el Golfo de Omán, se ha encontrado un recurso significativo de peces mesopelágicos de una alta reproductividad. Cada arrastrero puede capturar un promedio de 60 toneladas de pescado/día durante 250 días/año, que podrían ser materia prima para una planta de reducción. Estas cifras son conservativas, pues cuando la pesca es abundante, los arrastreros pueden capturar valores superiores al promedio. Se desea analizar y elegir cuál es la capacidad de materia prima diaria más conveniente entre dos plantas, cuyas capacidades nominales son: 250 y 500 t/día.
Solución: Se estudiaron las plantas de reducción con capacidad de 250 y 500 t de materia prima/día. Para ello, seleccionado el proceso de producción, se han calculado la inversión y los costos de producción, para diferentes capacidades en el corto y largo plazo, como se indican en la Tabla 5. 6.
Tabla 5.6 Ingresos y costos para plantas de harina de pescado
|
Capacidad |
250 t/día |
500 t/día | |||||
|
Materia prima (t/24 h) |
100 |
175 |
250 |
200 |
250 |
350 |
500 |
|
Ventas harina + aceite (US$ '000) |
3 025 |
5 294 |
7 562 |
6 050 |
7 562 |
10 587 |
15 125 |
|
Costos variables: planta + barcos (US$ '000) |
799 |
1 224 |
1 647 |
1 405 |
1 688 |
2 252 |
3 100 |
|
Costos fijos: planta + barcos (US$ '000) |
3 663 |
3 663 |
3 663 |
4 855 |
4 855 |
4 855 |
4 855 |
|
Costo promedio (US$/t) |
850 |
532 |
399 |
596 |
498 |
387 |
303 |
Una planta con 500 t/día de capacidad es mucho más flexible que una de 250 t/día. Por otra parte, el costo de una planta de 250 t no es muy diferente de aquélla de 500 t/día. El sobredimensionamiento de la planta es un factor de seguridad para que en los períodos de altas capturas, los arrastreros puedan suministrar hasta 90 t/día y esa captura pueda ser procesada en el transcurso del día. Una planta que produce con una capacidad reducida puede producir una harina con menor contenido graso y mayor contenido de proteínas.
Con 2 turnos de 8 horas la planta puede consumir hasta 240 t de pescado, permitiendo un correcto programa de limpieza y mantenimiento, interrumpiendo la producción 1 día por semana. Por otra parte, no puede pensarse que una planta con una capacidad nominal de 250 t/día, puede absorber esta cantidad en un promedio de 250 días/año, ni siquiera con operarios muy entrenados. Basándose en la experiencia, se ha determinado que la capacidad nominal puede utilizarse hasta el 70% en el transcurso de los 250 días por año. Esta cifra representa una producción promedio de 175 t de pescado/día. Las razones para reducir la capacidad real son:
- La capacidad real de la planta y la calidad de la harina de pescado son fuertemente dependientes de la frescura de la materia prima. Si la materia prima es muy vieja existen incrementos en las pérdidas y una disminución en la calidad de la harina. Si el pescado es muy fresco (esto es, en rigor mortis) existen problemas operativos para manejar y transportar la materia prima y la calidad de la harina resultante puede no ser aceptable para el consumidor.- El análisis de las posibilidades de captura de la zona muestra que la pesca de un arrastero consigna un valor promedio de 60 t/día. Si la captura es menor al referido promedio, ello no podrá ser compensado con una captura mayor en los días subsiguientes, en razón que la planta procesadora no podrá absorber dicho excedente.
- Una fábrica bien diseñada, detendrá su producción 1 vez/semana para limpieza y mantenimiento. Este hecho reduce el promedio de producción nominal diario.
- Una producción de 175 t/día para tres embarcaciones equivale a 58,3 t/día por barco, valor cercano a la capacidad de diseño (con un beneficio de US$ 400 000/año). Pero cuatro embarcaciones podrán capturar sólo 43,75 t/día, con fuertes pérdidas de eficiencia en la captura, totalizando en 250 días de producción, pérdidas por US$ 530 000.
En la Figura 5.15, se han graficado los resultados para los costos unitarios.
Figura 5.15 Costos promedio en el largo plazo para plantas de harina de pescado
Si las capturas se prevén con un mínimo de 60 000 t de pescada, se obtendrán promedios de 60 t por embarcación, cuando se cuenta con cuatro arrastreros, en 250 días de pesca/año. Estas capturas deben ser procesadas por una planta con capacidad nominal mayor de 250 t/día. Por estas razones se ha seleccionado la planta de 500 t/día (Arnesen y Schärfe, 1986).
5.5.1 Modelos matemáticos para la evaluación de recursos pesqueros
En la primera parte de este capítulo se ha analizado la microeconomía de la industria pesquera desde un punto de vista que podría considerarse como el punto de vista del dueño de la empresa. En el caso de capturas, no han sido impuestas condiciones biológicas a los cálculos realizados, esto es, nivel de disponibilidad de los recursos, aunque en la práctica este parámetro esté afectando las estimaciones. Sin embargo, dado que el pescado es un recurso renovable que depende de condiciones físicas y biológicas definidas, éstas deben ser tenidas en cuenta a fin de encontrar cómo debe operarse una pesquería como un sistema (no sólo un tipo de planta de procesamiento de pescado o un barco pesquero) en forma sustentable.
La microeconomía aplicada a pesquerías es ahora una rama bien desarrollada de la biología pesquera moderna, donde la interacción del conocimiento biológico y la microeconomía han dado paso al desarrollo de modelos matemáticos respecto a la economía de la sustentabilidad de una pesquería. Este enfoque permite la definición de límites útiles y condiciones de explotación de un recurso individual o de multi-especies y el establecimiento de políticas pesqueras (a ser aplicadas por los Gobiernos y/o autoimpuestas por los pescadores y la industria pesquera). Es tarea de cada pescador o empresa, ajustar su propio análisis microeconómico al análisis microeconómico general del recurso para que su explotación individual (y la del conjunto) sean sustentables. En la práctica, éste es uno de los problemas principales de las pesquerías actuales.
Se ha definido la función producción como la relación entre la cantidad de insumos utilizada y la cantidad de producto resultante. En términos de una pesquería, la función producción expresa la relación entre el esfuerzo de pesca aplicado y el pescado capturado. Como pesquería se considerará aquí la explotación del stock de una especie por un grupo de pescadores, embarcaciones o unidades de captura. En la práctica aparecen condiciones más complejas como son las pesquerías múltiples. La función producción en una pesquería, depende de la biología de reproducción del stock de peces. La mayoría de los tratamientos teóricos en economía de pesquerías utilizan el análisis definido originariamente por Schaefer (1954), donde el crecimiento del stock de peces se supone como una función del volumen expresado en unidades de peso.
La biomasa de un recurso pesquero inexplotado crecerá a distintas velocidades, dependiendo de su tamaño y aumentará hacia un tamaño máximo, el cual, una vez alcanzado permanecerá constante. Este tamaño de población se denomina tamaño de la población al estado virgen (Anderson, 1974). Los parámetros fisicoquímicos que influyen sobre este tamaño y la velocidad con la que el recurso se acerca a su punto máximo, son, entre otros: salinidad, temperatura, corrientes del agua, hábitos de alimentación de otras especies, velocidad de fotosíntesis, cantidad de energía solar radiada, velocidad a la que los elementos minerales son reemplazados.
Si se suponen estos parámetros como constantes, los tres componentes poblacionales que determinan el crecimiento del recurso son: reclutamiento (peso de la biomasa de peces que ingresan a la población capturable en un período de tiempo), crecimiento individual (el peso de la biomasa de cada pez individual en la población en ese período de tiempo) y mortalidad natural (el peso de la biomasa de peces de la población perdida debido a muerte natural y predación durante ese período de tiempo). El período de tiempo, normalmente, es de un año.
En el análisis de Schaefer se supone que el aumento de la biomasa de una pesquería es una función de la población que, puede graficarse con forma de campana como en la Figura 5.16(a). El eje horizontal mide el tamaño de la población y el vertical, el crecimiento por período, ambos en términos de peso.
Por ejemplo, cuando la población toma un valor P3, el incremento neto en tamaño o crecimiento será F3. Para stocks de pequeño tamaño, el efecto neto de reclutamiento y crecimiento individual es mayor que la mortalidad natural y el crecimiento natural es positivo, y aumenta con el tamaño del stock. Se alcanzará un punto en que el reclutamiento y el crecimiento individual balancearán la mortalidad natural y el crecimiento del stock se detendrá. Esta lucha entre fuerzas diferentes puede variar con las distintas especies, pero en general la curva de crecimiento mantendrá su forma de campana, aunque en algunos casos, el lado derecho de la misma puede acercarse asintóticamente al eje horizontal en una forma más o menos pronunciada.
De acuerdo con la Figura 5.16, P* es el tamaño de stock para el cual el reclutamiento y el crecimiento natural son compensados por la mortalidad natural. Por lo tanto, el tamaño de la población no aumentará más de ese tamaño. Este punto será el de equilibrio natural de la población. Para cualquier población menor, el crecimiento continuará hasta alcanzar el tamaño P*.
Cuando el hombre comienza a explotar una pesquería, se convierte en un predador que perturba el equilibrio de la población. Se alcanzará un nuevo punto de equilibrio donde el incremento neto en peso debido a factores naturales iguala la disminución neta debida a la mortalidad por pesca. En cualquier punto del tiempo, la captura o mortalidad por pesca será una función de la cantidad de esfuerzo de pesca que el hombre aplica a la pesquería y del tamaño del stock. Para cualquier tamaño de población, a mayor esfuerzo de pesca mayor será la captura; y para cualquier nivel de esfuerzo, a mayor población, mayor será la captura. Podemos graficar, la mortalidad debida a la captura como una función del esfuerzo si la población se mantiene constante, o como una función de la población, si el esfuerzo se mantiene constante.
Dado que la captura varía con cada nivel de esfuerzo, resultará un tamaño de población de equilibrio diferente para cada nivel de esfuerzo, Figura 5.16(b). Esto es importante pues el esfuerzo es una variable controlada por el hombre. La captura es una función del tamaño del stock y del esfuerzo, pero como el tamaño del stock en el equilibrio es una función del esfuerzo, entonces el rendimiento de pesca sustentable (F) es una función del esfuerzo únicamente. En la Figura 5.16 se han graficado 4 curvas punteadas que representan la cantidad de mortalidad por pesca (captura) en peso que ocurrirá durante un período para diferentes tamaños de población, correspondiendo cada una a un esfuerzo de pesca diferente.
La captura obtenida a partir de un nivel de esfuerzo y su correspondiente población de equilibrio se denomina Rendimiento Sustentable o Sostenido. Es sustentable porque el tamaño de la población no se afectará por la pesca, ya que la captura es equilibrada por el incremento natural del stock. Por lo tanto el mismo nivel de esfuerzo brindará el mismo nivel de captura en el próximo período. El conjunto de puntos que representan las capturas de rendimiento sustentable para cada nivel de esfuerzo se llama Curva de Rendimiento Sustentable.
Para la pesquería hipotética de la Figura 5.16, se obtendría la Figura 5.17(a). El eje vertical mide captura en peso y el eje horizontal mide el esfuerzo, tal como se representaría una función típica de producción en el corto plazo, con esfuerzo como insumo variable.
También son importantes los conceptos de rendimiento sustentable promedio y marginal, cuyas curvas se han graficado en la Figura 5.17(b). Estos conceptos también son comparables con los productos promedio y marginal. El rendimiento sustentable promedio, que es el rendimiento sustentable por unidad de esfuerzo de pesca, F/E, disminuye continuamente hasta que alcanza el valor cero al mismo nivel en que se hace cero el rendimiento total.
El rendimiento sustentable marginal, que es el cambio en el rendimiento sustentable debido a un cambio en el esfuerzo de pesca, o (D F/D E), es positivo pero declina y alcanza cero al nivel en que se obtiene el Rendimiento Máximo Sustentable. Luego se hace negativo. Esto implica que adicionales niveles de esfuerzo por encima del punto de RMS, realmente disminuirán las capturas.
Figura 5.17 Curvas de rendimiento sustentable total, marginal y promedio
La curva de Rendimiento sustentable puede considerarse la función producción de una pesquería, en el largo plazo. Es decir, mostrará la cantidad del recurso que puede ser "producida" con una base sostenida a distintos niveles de esfuerzos: cambios en el esfuerzo producirán un cambio en el tamaño de equilibrio de la población, pero deberá pasar un tiempo antes de que el nuevo equilibrio sea alcanzado.
En los casos en que esta demora en el tiempo es importante, las curvas de rendimiento para niveles específicos de población pueden ser utilizadas como funciones de producción en el corto plazo, como las graficadas en líneas punteadas en la Figura 5.17(a) son inversas a las curvas de captura y población graficadas en la Figura 5.16(a). Una curva diferente es necesaria para cada tamaño de población. De las dos curvas mostradas, la más alta es la que corresponde a la población mayor (P2 y P3 son las mismas que en la Figura 5.16).
Para poder evaluar el estado de un recurso pesquero, determinar el volumen de capturas que se pueden obtener y estimar los efectos de las distintas alternativas de pesca, se deben cuantificar los efectos que tiene la pesca sobre el recurso pesquero, representando matemáticamente los posibles cambios de las poblaciones ante las diversas alternativas de explotación (Csirke, 1988).
El concepto general sobre el cual se han desarrollado todos los modelos de dinámica de poblaciones que se usan para evaluar los recursos pesqueros y recomendar medidas de ordenación puede ser simplificado por la siguiente fórmula:
F2 = F1 + (R + G) - (M + C) .......... (5.16)
donde F1 y F2 representan respectivamente la biomasa de la población al inicio y al final de un período determinado; R, la cantidad de recluta o de nuevos individuos que han ingresado a formar parte de la población; G, el incremento en peso causado por el crecimiento de los peces existentes en la población; M, la cantidad de peces muertos por causas naturales; y C, la cantidad de peces capturados o muertos por la pesca en ese mismo período de tiempo.
De acuerdo a este modelo, la población se mantiene en equilibrio en tanto el incremento natural de la población (R + G) se mantenga igual a la disminución (M + C) producida por las causas naturales y por la pesca, de otra forma la población tiende a aumentar o a disminuir según sean mayores los incrementos o las disminuciones.
De todos estos parámetros, el único que puede ser controlado por el hombre es la captura (C), a través de la cual se puede modificar el tamaño de la población en períodos sucesivos (F2, F3, ...Fn). Una de las preocupaciones de cada comunidad pesquera es la determinación del nivel máximo de captura (C) y del tamaño de la población (Ft) que, manteniéndose en equilibrio (es decir, considerando M + C = G + R), permita obtener las capturas máximas.
Los métodos que generalmente se aplican para estimar el tamaño de una población y la posible relación entre la tasa de incremento natural y la intensidad y condiciones de explotación (por ejemplo, tasa de explotación, edad a la primera captura, etc) se pueden agrupar en métodos analíticos o estructurales y métodos sintéticos o globales.
Los métodos analíticos o estructurales sirven para investigar el tamaño y la dinámica de la población a partir de sus componentes principales y los cambios que ellas experimentan. En cambio, los métodos sintéticos, mejor representados por los modelos globales de producción, son aquéllos que tratan a la población como una gran caja negra donde no se consideran los cambios que ocurren internamente y sólo se analiza la relación entre el estímulo, que suele ser representado por la intensidad (o esfuerzo de pesca), y las capturas totales y la captura por unidad de esfuerzo (o respuesta) obtenida.
Se analizarán los siguientes métodos analíticos:
- Modeló de rendimiento por reclutamiento
En la aplicación del modelo de rendimiento por reclutamiento (Ricker, 1975; Gulland, 1969; Csirke, 1980; Pauly, 1980) se utiliza la información, datos y muestras obtenidas de la pesca comercial y, si existen, de las pescas exploratorias, para estimar los parámetros poblacionales. De todos los parámetros, los únicos que pueden ser controlados voluntariamente por el hombre son la mortalidad por pesca, que se asume proporcional al esfuerzo de pesca (número de barcos, pescadores, etc) y el tamaño o edad en que los peces comienzan a ser capturados (que puede ser modificada cambiando el tamaño de las redes, evitando las zonas de cría, etc).
Si se conocen estos parámetros, se puede emplear una ecuación más o menos compleja propuesta por Beverton y Holt (1957) o algunas de las versiones modificadas propuestas por otros autores, para estimar la captura promedio que puede rendir cada recluta bajo cierta combinación de valores de mortalidad por pesca y edad a la primera captura. Si se conoce la fuerza del reclutamiento será posible estimar también la captura potencial total de toda la clase anual y de la población.
- Análisis de población virtual (APV)
El método de análisis de población virtual permite reconstruir la historia de una clase anual (que al ser sumada a las otras clases anuales permite reconstruir la historia de toda la población) a partir de las capturas y mortalidad natural estimada de esa clase anual durante el tiempo que fue explotada y la mortalidad por pesca y abundancia durante el último año o temporada de pesca. De esta forma, haciendo un análisis retrospectivo de las capturas de cada clase anual a través del tiempo, se llega a estimar el número de individuos que estuvieron presentes en la población en el pasado.
Para aplicar este método se necesita conocer, para cada grupo de cierta edad, la captura total y la mortalidad natural en cada año, además de la mortalidad por pesca o abundancia para la última temporada de pesca. Luego se aplican una serie de ecuaciones que se presentan y discuten en detalle en las obras de Gulland (1971), Pope (1972) y Cadima (1978) para estimar el tamaño de cada clase anual y de la población que existió en el pasado, u otros métodos disponibles cuando no se dispone de series temporales de valores para capturas y esfuerzo (García et al, 1989).
Dentro de los métodos globales de producción, se analiza áquel que se basa en la ley de crecimiento de poblaciones al estado natural que siguen una curva sigmoidea. Schaefer (1954) propuso un método para estimar la producción capturable de una población de peces relacionando la producción excedente o rendimiento sostenible a una medida de la abundancia de la población o la mortalidad por pesca.
Este modelo parte del supuesto que bajo condiciones de equilibrio, la abundancia o captura por unidad de esfuerzo (Ut) disminuye en forma lineal con los incrementos en el esfuerzo de pesca (E). Esta relación puede ser representada por la ecuación:
Ut=U¥ - b × Et .......... (5.17)
donde representan: Ut, la abundancia; Et, el esfuerzo de pesca en un momento determinado; U¥ , el índice de la capacidad de carga o tamaño de la población al estado virgen y b es una constante.
A partir de esta ecuación y definiendo la abundancia proporcional a la captura por unidad de esfuerzo (U = Y/E), se puede derivar la siguiente relación entre la captura (Y) y el esfuerzo de pesca (E):
Yt = U¥ × Et - b × Et2 .......... (5.18)
que describe una parábola, donde cada punto de la curva corresponde a un nivel de captura o rendimiento de equilibrio (Y) correspondiente al nivel de esfuerzo (Et) determinado. El punto máximo de la parábola es lo que se conoce como Rendimiento Máximo Sustentable o Captura Máxima Sustentable.
La simplicidad de los fundamentos teóricos y el hecho de requerir sólo datos de captura y esfuerzo de pesca (datos estadísticos fáciles de obtener y que también son empleados para otros fines y por otros usuarios) causaron que los modelos de producción y la recolección de datos de captura y de esfuerzo se convirtieran en el método estándar en el análisis y evaluación de muchas pesquerías, no sin que esto llevara en muchos casos a conclusiones erradas por la falta de información complementaria.
En años más recientes, Pella y Tomlinson (1969) y Fox (1970) han propuesto algunas versiones modificadas de este modelo para adaptarlo a aplicaciones específicas y mejorar los ajustes en casos particulares. Más recientemente, Csirke y Caddy (1983) propusieron también una versión modificada que permite aplicar este tipo de modelo a pesquerías de las cuales sólo se cuenta con datos de captura o índices de abundancia y estimados de la mortalidad total, lo cual resulta particularmente útil en los casos en que no existen datos adecuados.
Las conclusiones que se obtienen del análisis de las características de la dinámica de las poblaciones de peces deben ser expresadas en términos que puedan ser utilizados por quienes sin ser biólogos, tienen la responsabilidad de planificar u ordenar el desarrollo pesquero. Es por ello que se han formulado modelos en forma que se puedan expresar los resultados relacionando las capturas de equilibrio con los distintos valores de mortalidad por pesca, los que, por motivos prácticos normalmente se representan por su correspondiente valor de esfuerzo de pesca (por ejemplo, número de barcos, viajes, horas de pesca, número de pescadores, etc) (Csirke, 1985).
La ventaja de expresar los resultados en términos de captura y esfuerzo son claras, ya que son precisamente éstas las unidades con que los responsables de la ordenación de la pesca tienen que tratar continuamente. La forma exacta de la curva que relaciona la captura con el esfuerzo, y la que relaciona la captura por unidad de esfuerzo (abundancia aparente) con el esfuerzo pueden cambiar según el modelo específico que se use y el tipo de pesquería que se analice, pero en general, estas dos curvas tienen la forma que aparece en la Figura 5.17.
La conclusión general que se puede extraer con respecto a la relación entre la captura y el esfuerzo es que, si se parte de cero, a pequeños incrementos del esfuerzo sigue un aumento casi proporcional de las capturas. Sin embargo, la tasa de incremento de la captura comienza a declinar a mayores valores del esfuerzo, (la captura por unidad de esfuerzo también disminuye) llega a cero y después se hace negativa al lado derecho de la curva entrando en lo que se reconoce como nivel de sobre-explotación.
El punto donde el incremento de la captura con respecto al incremento del esfuerzo es cero corresponde al nivel de la Captura o Rendimiento Máximo Sustentable (RMS), que representaría el nivel óptimo de explotación si el objetivo de la pesca es obtener la mayor captura posible en forma sustentable.
Las consideraciones económicas y sociales sobre sustentabilidad están recibiendo ahora mayor atención y las implicancias de considerar estos aspectos se pueden apreciar en la Figura 5.18. La Figura 5.18(a), representa la relación entre el valor bruto de la captura (eje de las abcisas) y los costos totales de explotación (eje de las ordenadas).
El valor bruto de la captura es máximo en el Punto B. En el Punto A, el valor bruto de la captura es igual a los costos de operación, con lo cual la rentabilidad es cero. La máxima rentabilidad económica (rendimiento económico neto máximo) se logra en el Punto C. Desde el punto de vista económico, éste es el nivel óptimo de captura, pero en base a consideraciones de otro tipo (por ejemplo, maximizar las capturas totales) se puede llegar a autorizar el ingreso de nuevas unidades de pesca hasta llegar al Punto B. Inclusive en ausencia de una buena política de ordenación de la pesca, se puede llegar a un nivel de equilibrio donde el valor de la captura es igual a los costos totales (Punto A). En casos extremos la pesquería puede también llegar a estabilizarse en un nivel de captura más reducido donde el valor de las capturas sólo sirve para cubrir los costos corrientes (gastos de combustible, salarios, seguros, mantenimiento de las embarcaciones y artes de pesca, etc.) y ante la falta de amortización y reinversiones la pesquería corre el peligro de entrar en un proceso de degradación gradual.
La Figura 5.18(b) muestra otros índices económicos. La pendiente de línea contínua representa el rendimiento económico marginal o valor neto agregado a la captura total con la incorporación de cada nueva unidad de pesca (y el incremento correspondiente del costo total de pesca). El rendimiento marginal muestra el valor agregado a toda la pesquería en su conjunto por la adición de una unidad de esfuerzo adicional (por ejemplo, la incorporación de un nuevo barco). Al inicio el rendimiento marginal es alto pero comienza a disminuir rápidamente a medida que la intensidad de pesca aumenta. En un cierto punto, el rendimiento marginal será igual al costo de la nueva unidad de pesca (Punto C); ese es el nivel al cual el rendimiento económico neto es máximo.
Figura 5.18 Curvas de ingreso y de costo totales, marginales y promedio
Este es probablemente el punto en el cual se debería mantener la pesca si se quiere maximizar el rendimiento económico neto ya que cualquier incremento en el esfuerzo de pesca costará más que el correspondiente incremento en el valor total producido por la pesca y obviamente no sería rentable si se considera la pesquería en su conjunto. Sin embargo, el criterio utilizado para determinar si se construye o se permite el ingreso de un nuevo barco es normalmente el potencial de captura de ese barco y no el incremento en la captura total para toda la flota en su conjunto. El incremento de una nueva unidad de pesca puede de hecho ser menor debido a que las actividades de un nuevo barco pueden llegar a reducir en cierta medida la abundancia (c.p.u.e.) de la población que se está explotando y así reducir las capturas de los otros barcos. Este es un aspecto muy importante que debe ser considerado cuando se plantee el incremento del esfuerzo de pesca y el desarrollo de una determinada pesquería (Csirke, 1985).
Así como es posible incorporar criterios de orden económico en los modelos de dinámica de poblaciones se pueden también incorporar criterios de orden social que tiendan a maximizar el número de puestos de trabajo, número de unidades de pesca, etc. Los modelos de dinámica de poblaciones dan información útil sobre los límites hasta los cuales puede desarrollarse una pesquería y cuáles son las consecuencias para la población y para el hombre mismo de aumentar o disminuir el número de unidades de pesca.
Cuando se trata de una pesquería no regulada, el nivel de esfuerzo del equilibrio en la pesquería será E3, donde los ingresos totales igualan los costos totales. También es el punto donde los ingresos promedio por unidad de esfuerzo igualan los costos promedio por unidad de esfuerzo. En este punto, los ingresos totales de la pesquería a la izquierda de E3 son mayores que el costo total. Por lo tanto, cada embarcación tendrá beneficios, o lo que es lo mismo, los ingresos promedio por unidad de esfuerzo son mayores que el costo promedio por unidad de esfuerzo. Esta situación provocará no sólo que las embarcaciones existentes expandan su esfuerzo sino que motivará a nuevas unidades a entrar a la pesquería. El caso contrario se presenta a la derecha de E3. Dado que el esfuerzo tiende a aumentar por debajo de E3 y a disminuír por encima de ese punto, el nivel de equilibrio de esfuerzo en una pesquería de libre acceso se estabilizará en ese punto.
También, éste puede ser denominado un punto de equilibrio bioeconómico. El nivel de esfuerzo no cambiará a menos que varíen los precios o costos y también permanecerá constante la población. El uso adecuado de un recurso requiere que el mismo sea utilizado de manera tal de maximizar su rendimiento neto. Esto garantiza que la producción sea maximizada. En la Figura 5.18, esta situación se da en el punto E1, donde el beneficio anual de la pesquería (diferencia entre ingresos y costos) es un máximo. Cualquier incremento en el esfuerzo por encima de E1 disminuirá los beneficios anuales, pues los costos aumentarán más que los ingresos.
Los ingresos miden lo que la población está dispuesta a pagar por el pescado, y los costos representan el valor del costo de oportunidad para esos insumos necesarios para producir el esfuerzo usado para capturar el pescado. Por lo tanto, cuando el costo marginal del esfuerzo es mayor que los ingresos marginales, la empresa está perdiendo, ya que se está obteniendo pescado adicional a un costo mayor de lo que vale para los consumidores. En otras palabras, cuando el esfuerzo aumenta, los insumos están siendo desviados de producir otros bienes más valiosos para la empresa.
Por otro lado, si el esfuerzo se redujera, el beneficio disminuirá lo que implicaría que los ingresos están disminuyendo más rápido que los costos. Por lo tanto, aunque los recursos podrían ser usados para otro tipo de producción, los bienes resultantes tendrán un valor menor que el del pescado que podría haber sido capturado con E1. Este punto es denominado Rendimiento Máximo Económico de la pesquería. Es importante remarcar que lo que es deseable del punto de RME no es que sea máximo el beneficio de la pesquería en su conjunto, sino que los insumos de la sociedad no sean usados para explotar la pesquería a menos que no puedan ser usados más ventajosamente en otra parte.
La mayoría de los recursos de la pesquería de pequeña escala pueden ser explotados por cualquiera que desee hacerlo. Este acceso natural abierto de la pesquería tiende a conducir a una sobrepesca biológica (más allá del RMS) y a una sobrepesca económica (más allá del RME), hacia punto donde el costo total de la pesca es igual al ingreso total obtenido de la pesca. Mientras que el RME puede en raros casos estar a la derecha del RMS, el beneficio máximo económico para la nación resultante de la actividad pesquera es generalmente alcanzado a la izquierda del RMS. Un punto en la curva que relaciona el rendimiento con el tamaño del recurso y la cantidad de esfuerzo pesquero que se localiza a la derecha del RMS denota esfuerzo pesquero adicional y un tamaño menor de la población; un punto a la izquierda del RME, denota un menor esfuerzo y un tamaño mayor de la población.
Similarmente, la teoría de desarrollo sustentable puede ser aplicada al caso de una pesquería o de un recurso natural renovable. Este nuevo concepto de desarrollo tendrá éxito si los aspectos bilógicos, económicos, políticos y culturales son tenidos en cuenta simulatáneamente. Pueden ser definidos como un grupo de objetivos cuyo cambio en el tiempo debe ser positivo. Algunos de los objetivos son incremento del ingreso real per cápita, mejoramiento del nivel sanitario y nutricional de la población, expansión y extensión de la educación, aumento de recursos (naturales o producidos por el hombre), una distribución de ingresos equitativa, y un incremento de las libertades básicas. El hecho de alcanzar estos objetivos está sujeto a la condición de que el stock de capital natural no debe disminuir con el tiempo. Una definición comprensiva de capital natural involucra todos los recursos naturales, desde petróleo hasta la calidad del suelo y las aguas continentales, los stocks de pescado en el océano, y la capacidad del planeta para reciclar y absorver dióxido de carbono. Si esta teoría se aplica al tratamiento de una pesquería, se deriva la siguiente ecuación:
(dR/dX) × (1/p) = P - C(X) ......... (5.19)
donde:
R = [P - C(X)] × Y(t), ingreso sustentable o beneficio de la actividad
x = crecimiento del stock
p = tasa de interés
P = precio del recurso natural
C = costo unitario de captura
Y(t) = captura
Su deducción y las modificaciones cuando el precio varía, están dadas en la Referencia (Pearce et al., 1990). En realidad existen escasos datos sobre tasas de crecimiento de recursos lo que impide todo análisis de RME. A fin de estudiar los ingresos y costos de una pesquería se necesitan 3 clases de datos: (1) una estimación de la curva de rendimiento sustentable, (2) una estimación del costo promedio del esfuerzo y (3) una estimación del precio del recurso.
A partir del modelo de Schaefer, la curva de rendimiento sustentable puede ser expresada matemáticamente como:
Y = c × E - d × E² ......... (5.20)
donde:
Y = captura
E = esfuerzo de pesca
c y d, constantes
Usando técnicas matemáticas usuales, puede demostrarse que el RMS sera igual a c²/4d y será obtenida cuando el esfuerzo es igual a c/2d.
Para aplicar la ecuación del modelo a una pesquería es necesario obtener estimados de c y d. De la ecuación de rendimiento sostenible, el rendimiento sostenible promedio por unidad de esfuerzo puede expresarse como:
Y/E = c - d × E .......... (5.21)
Por lo tanto, a partir de datos de captura y esfuerzo total sobre un período de años, pueden obtenerse los estimados de c y d, con la técnica de cuadrados mínimos.
Ejemplo 5.4 Pesquería de langostas en el norte de EE.UU (1950-66)
Esta secuencia fue aplicada al caso de la pesquería de langostas en el norte de Estados Unidos para obtener un panorama rudimentario de la operación de pesquerías de libre acceso y recomendar políticas de regulación (Bell y Fullenbaum, 1973; Fullenbaum y Bell, 1974). A partir de datos entre 1950 y 1966 de captura y esfuerzo, se estimó la siguiente ecuación:
Y/E = - 48,4 - 0,000024 × E + 2,126 × °F ......... (5.22)
De acuerdo con esta estimación, un incremento de 100 000 trampas disminuiría la captura anual por trampa en 2,4 lb y un aumento en la temperatura de 1°F aumentaría la captura en 2,126 lb. Si se utiliza la temperatura promedio de 1966 de 46°F, que es cercana al promedio de los últimos 65 años, se obtiene como resultado que el RMS sería de 25,459 millones de libras y se obtendría para un total de 1 030 000 trampas. Esto significa:
Y = 49,4 × E - 0,000024 × E2 ......... (5.23)
Conociendo el costo de operación de una embarcación y el número de trampas promedio que lleva cada una, se puede expresar el costo total (CT) como una función del esfuerzo del siguiente modo:
CT = 21,43 × E .......... (5.24)
y si se divide por el rendimiento total, se obtiene el costo promedio:
Resolviendo la ecuación cuadrática (5.23) para obtener E = f(Y) y reemplazando en la ecuación (5.24) ó (5.25), se obtiene una ecuación en función exclusivamente de Y. Asimismo, se debe estimar el costo marginal en términos del rendimiento, como la derivada de la ecuación del costo total. Si se analizan los resultados, se observa que al aumentar el número de trampas, el rendimiento total disminuye, pero el costo promedio por libra continúa aumentando dado que se está gastando más dinero para obtener menor rendimiento.
Para la determinación del punto de equilibrio, se debe considerar la siguiente curva de demanda resultante de la aplicación de las técnicas estándar de econometría, con datos de precios de desembarque de langostas, ingreso de los consumidores, población de EE.UU, índice de precios al consumidor, consumo total, importaciones totales y producción total de langostas en EE.UU comparada con la producción del norte.
Precio = 0,9393 - 0,005705 × Y .......... (5.26)
Al analizar la ecuación de demanda (5.26), se observó que si las langostas capturadas aumentaban en 1 millón de libras, el precio disminuía en menos de medio centavo por libra. El punto de equilibrio surge de igualar la ecuación de la demanda a la curva de costo promedio. En su intersección, se obtiene un precio de US$ 0,7952 y una masa total capturada de 25,24 millones de libras. Para obtener ese rendimiento deben utilizarse 933 000 trampas. Los números reales de 1966 fueron: US$ 0,762, 25,6 millones de libras y 947 113 trampas.
El RME ocurre en la intersección de la curva de costos marginales con la curva de demanda. El precio de equilibrio resultó de US$ 0,833, con un rendimiento total de 18,57 millones de libras, usando 490 000 trampas. El costo promedio por libra, operando a este nivel de producción era US$ 0,571. Los ingresos totales en este punto, igual a la diferencia entre precio de venta y costo multiplicada por el rendimiento total fueron de US$ 4 865 340.
Otra conclusión sería la siguiente: si la producción de la pesquería se debía reducir de 25,24 a 18,57 millones de libras, disminuyendo el número de trampas de 933 000 a 490 000, esto conduce a una reducción de los costos promedio por libra de US$ 0,7952 a US$ 0,571, para una disminución combinada en el costo total de US$ 9 467 378. Esta reducción implica, con el concepto de costo de oportunidad, que hay bienes por este valor que pueden ser producidos en otras partes de la economía.
Al mismo tiempo, la reducción en el rendimiento total causaba un aumento del precio, y una disminución del consumo de langostas, con una pérdida de US$ 4 602 038. Descontando esta cantidad del incremento en la producción de bienes en otras áreas, se encuentra que moverse al punto de RME permitía a la sociedad obtener un beneficio neto de US$ 4 865 340, igual a la renta de la pesquería cuando se operaba en el RME (Anderson, 1974).
Las empresas pesqueras deben tener una comprensión adecuada del manejo microeconómico de la pesquería total, ya que de ello depende el desarrollo y el funcionamiento de su empresa en el tiempo. Es también conveniente que este conocimiento se de dentro de las asociaciones o cámaras de pescadores ya que se trata de un problema común.
Otro ejemplo de aplicación de estos conceptos fue la pesquería de Chipre (Hannesson, 1988), donde el esfuerzo se midió en unidades de días de pesca. El óptimo esfuerzo se encontró para 105 días de pesca por milla cuadrada para algunas áreas de pesca y 175 para otras. Estos niveles están muy por debajo de los niveles reales de operación de la flota, 67% de los niveles promedio de 1983-1984 y 58% del nivel de 1984. Asimismo, se han calculado los beneficios económicos, correspondiendo el esfuerzo óptimo a una captura total de 1 360 t. Esto puede ser comparado con la captura real en años recientes en Chipre, que van desde 1 038 t en 1980 hasta 1 952 t en 1984.
Sobre la base de estos resultados, se han analizado distintas políticas que pueden proponerse para reducir el nivel de esfuerzo pesquero hasta los niveles óptimos. Uno de estos métodos es reducir gradualmente el nivel de esfuerzo, siendo el primer paso, detener el aumento de esfuerzo. Es evidente que deberán tenerse en cuenta las alternativas de empleo de aquéllos que dejan la pesquería.
Esta reducción del esfuerzo de pesca puede alcanzarse dividiendo la captura total en cuotas individuales, por limitación de licencias de pesca, imponiendo un impuesto del recurso para la pesca, por exclusión de algunos pescadores ocasionales, especificando zonas de validez de los permisos de pesca. Se ha propuesto otorgar licencias o cuotas de pesca a los pescadores activos en el momento en que se introduce la regulación, y luego comprar cuotas o licencias en la medida que sea necesario hasta alcanzar el esfuerzo de pesca óptimo.
El tema de la microeconomía de una pesquería en su conjunto, y de las diversas posibilidades para su regulación ha sido extensamente estudiado (Csirke, 1985; Doubleday, 1976; Gulland, 1974; Gulland y Boerema, 1973), los autores refieren al lector interesado a dichas referencias.