Este capítulo tiene por finalidad posibilitar la selección de alternativas, donde se requiera el uso de capital durante cierto tiempo, tales como proyectos de ingeniería o negocios en general. En esos casos, es esencial considerar el efecto del tiempo sobre el capital, en virtud de que este último debe poseer siempre un rendimiento. Si no se tienen en cuenta en forma adecuada las relaciones dinero-tiempo, los resultados de los estudios económicos son inexactos y conducen a decisiones equivocadas. El Apéndice B presenta una revisión concisa de ecuaciones financieras, necesarias para el cálculo de interés y valor temporal del dinero.
6.1.1 Análisis de valor presente
6.1.2 Punto de equivalencia
6.1.3 Técnicas de optimización
No obstante que la experiencia, intuición y juicio son todavía ingredientes predominantes en las decisiones, tanto gerenciales como a nivel producción, se ha logrado un progreso significativo en el empleo de técnicas cuantitativas. Estas ayudan al proceso de la toma de decisión, mediante el uso de modelos económicos. El análisis directo de los procesos operativos alternativos es usualmente costoso y, en muchos casos, imposible. No obstante, los modelos de decisión y los procesos de simulación proveen un medio adecuado donde el evaluador puede obtener información de operaciones bajo su control sin perturbar las operaciones en sí mismas. Como resultado de ello, el proceso de simulación es esencialmente un proceso de experimentación indirecta a través del cual se testean cursos de acción alternativos antes de ser implementados.
Los modelos de decisión económica son formulados para proveer al analista con una base cuantitativa para estudiar las operaciones bajo su control. El método está compuesto de cuatro etapas:
- Definir el problema
- Formular el modelo
- Ejecutar el modelo
- Tomar la decisión
La metodología aplicada en cada caso depende de su naturaleza, y de una definición clara del objetivo perseguido. Entre las metodologías disponibles se pueden mencionar:
- Selección de alternativas a través del análisis de valor presente o punto de equivalencia.
- Técnicas de optimización
- Métodos de cálculo de rentabilidad de proyectos
- Análisis del punto de equilibrio
El análisis de valor presente y punto de equivalencia será discutido en el presente capítulo, mientras que también se ha incluido una breve introducción a técnicas de optimización. Los métodos de cálculo de rentabilidad de proyectos y análisis de punto de equilibrio serán discutidos en el próximo capítulo.
El criterio de decisión debe incorporar algún índice, medida de equivalencia o base para su comparación, que resuma las diferencias significativas entre las distintas propuestas. Las relaciones y ecuaciones desarrolladas en este capítulo, son los elementos necesarios que permiten realizar las comparaciones entre dos o más alternativas que tienen igual o diferente vida útil. Los datos requeridos, entre otros, son: inversión inicial, gastos operativos uniformes o irregulares, valor residual y vida útil.
Las alternativas que se pueden dar, son el resultado de considerar diferentes sumas de dinero en relación a distintos tiempos, dentro de la vida útil de las mismas. Para posibilitar la selección más apropiada, dichas alternativas deben ser reducidas a una base temporal común, entendiéndose como tal, la comparación realizada en el mismo punto del eje temporal. Las bases más comunes de comparación son:
- Valor presente: la comparación es realizada entre cantidades equivalentes computadas en el tiempo presente.- Costo anual uniforme: la comparación es realizada al final del año entre cantidades anuales uniformes equivalentes (base temporal: un año)
- Costo capitalizado: la comparación es realizada con la premisa de disponer de los fondos necesarios para reponer el equipo una vez cumplida su vida útil (base temporal: infinita).
Ejemplo 6.1 Selección de alternativas con vidas útiles iguales. Descabezado, eviscerado y etiquetado manual y mecánico en pequeñas plantas de conservas de pescado
Analizar la siguiente propuesta: Sustituir maquinaria por mano de obra en las operaciones de descabezado-eviscerado y etiquetado, para pequeñas plantas de conservas en países tropicales. La capacidad de producción es de 10 000 latas de 125 g de sardinas cada 8 horas. En la Tabla 6.1 se muestran las inversiones y costos de operación para cada alternativa. Se adopta como valor temporal del dinero el 10% anual. Bajo estas condiciones, la pregunta que cabe es determinar la decisión más satisfactoria desde el punto de vista económico. Expresar el resultado como valor presente y costo anual uniforme.
Tabla 6.1 Inversión y gastos de operación para las alternativas A y B
|
|
Alternativa A |
Alternativa B |
|
Inversión (US$) |
172 930 |
154 006 |
|
Costo de la mano de obra (US$/año) |
42 408 |
71 714 |
|
Costo de mantenimiento (US$/año) |
7 965 |
7 022 |
|
Consumo de electricidad (US$/año) |
1 262 |
942 |
|
Seguros (US$/año) |
1 596 |
1 398 |
|
Vida útil (años) |
10 |
10 |
Solución:
|
Valor presente = PA10 |
= 172 930 + (42 408 + 7 965 + 1 262 + 1 596) × FAP10%,10 = |
|
|
= 172 930 + 53 231 × 6,15 = US$ 500 300 |
Valor presente = PB10 = 154 006 + 81 076 × 6,15 = US$ 652 623
donde FAP10%,10 es el factor de valor presente con serie de pagos iguales para una tasa de interés (i) igual al 10% y un período n = 10 (véase el Apéndice B, Tabla B.2).
Costo anual uniforme = AA = PA10 × FAP10%,10 = 500 300 × 0,163 = US$ 81 450
Costo anual uniforme = AB = PB10 × FAP10%,10 = 652 623 × 0,163 = US$ 106 377
donde FAP10%,10 es el factor de recuperación para i = 0,10 (10%) y n = 10
(FPA10%,10 = 1/FAP10%,10) (véase el Apéndice B, Tabla B.2).
El efecto económico de la sustitución de equipos por mano de obra depende del costo de la mano de obra adicional en relación al desembolso de capital. Con los datos precedentes, la alternativa B de mano de obra intensiva produce un costo superior (30%). Sin embargo, podría considerarse que el beneficio social resultante del aumento de empleo, compensa con plenitud esta desventaja económica, e inclina la balanza para la adopción de técnicas de mano de obra intensiva (Edwards, 1981).
Ejemplo 6.2 Selección de alternativas con distintas vidas útiles. Secado natural y mecánico
Analizar el secado natural o mecánico de pescado pequeño de agua dulce en un país de Africa oriental (Waterman, 1978). La producción anual es de 53 t, con un rendimiento del 32,5%, trabajando 250 días por año a plena capacidad durante 12 horas por día. El producto es vendido a granel sin embalajes. El secado mecánico se efectúa en un túnel de secado a pequeña escala, indirectamente calentado mediante aceite diesel con circulación de aire forzada y el ciclo de secado dura 12 horas. Se estima una vida útil promedio de 10 años. Deben considerarse los consumos de combustible, electricidad y mano de obra.
El secado al sol se efectúa en bastidores construidos en madera y malla de alambre, cuya vida útil es de un año. Se extienden poco más de 5 kg de pescado sobre 1 m2 de bastidor y el ciclo de secado dura 5 días. En este procedimiento se emplea el doble de mano de obra. La Tabla 6.2 consigna todos los valores de inversión y costos. Expresar el resultado como valor presente y costo anual uniforme.
Tabla 6.2 Inversión y costos para secado mecánico y secado natural
|
|
Alternativa C |
Alternativa D |
|
Inversión (US$) |
9 000 |
720 |
|
Costo de la Mano de Obra (US$/año) |
375 |
750 |
|
Costo de Mantenimiento (US$/año) |
1 200 |
360 |
|
Consumo de electricidad (US$/año) |
4 440 |
- |
|
Vida útil (años) |
10 |
1 |
Solución:
PC10 = 9 000 + (1 200 + 4 440 + 375) × FAP10%,10 = US$ 45 992PD1 = 720 + (750 + 360) × FAP10%,1 = US$ 1 729
donde FAP10%,1 es el factor de valor presente para i = 0,10 (10%) y un período de un año (n = 1).
No sería equitativo comparar el valor presente del costo de 10 años de servicio para la alternativa C con el valor presente del costo de un año de servicio para la alternativa D. Aplicaremos la fórmula siguiente, ya que nos permite la conversión del valor presente de una alternativa con un período de vida útil (n) a su valor presente equivalente para cualquier otra vida útil (k).
donde FPA10%,n es el factor de recuperación de capital en n períodos y FPA10%,k es el factor de recuperación de capital en k períodos.
La Ecuación (6.1) fue desarrollada por Jelen (1970). Numéricamente, el valor presente de los costos de la alternativa D para una duración de 10 años es:
Expresado en base anual, (véase la ecuación de P a A en la Tabla B.2, Apéndice B), los valores son:
AC = US$ 7 492 y AD = US$ 1 901
La comparación económica demuestra que el secado natural tiene una diferencia anual favorable de US$ 5 591 frente al secado mecánico, aún cuando los cálculos están ajustados por diferencias en la vida útil. Además, en la práctica, cada comparación contiene elementos intangibles. En este caso, para obtener una buena elaboración de productos secados naturalmente en climas tropicales, debemos considerar lo siguiente: temperatura y humedad del aire, materia prima magra o grasa, duración de la temporada de lluvias, características y condiciones del mercado donde el pescado es comercializado, etc. Si a todos estos elementos se le pueden asignar valor monetario, ellos podrían incluirse en el análisis cuantitativo y modificar substancialmente el resultado.
No obstante, con respecto al secado de pescado, la diferencia económica a favor del secado natural continúa siendo muy grande en muchas situaciones prácticas, y ésta es la razón para que no se hayan adoptado nuevos métodos tecnológicamente avanzados de secado en países en desarrollo, a pesar del esfuerzo de agencias de desarrollo (nacionales e internacionales). Cabe consignar que el secado natural de pescado es aún utilizado en Japón y algunos países escandinavos.
Para la situación en que los costos puedan ser expresados en función de una variable de decisión común (número de unidades de producción, tiempo de operación, etc.), estas alternativas pueden evaluarse analítica o gráficamente por aplicación del siguiente criterio. Punto de equivalencia: es el valor de la variable de decisión común para el cual, los costos de ambas alternativas son iguales.
Es factible aplicar este modelo de decisión, para las siguientes opciones:
1. Ante la perspectiva de un nuevo producto, se necesita analizar cuál es el volumen de producción donde resultan equivalentes los costos de ampliar la capacidad frigorífica existente con los costos de requerir los servicios de frigoríficos cercanos; es decir, producir frío o comprarlo;2. Ante un requerimiento de un cliente, se hace necesario disponer de una nueva máquina, y se debería conocer cuál tendría que ser el tiempo de operación mensual para que resulte más beneficioso comprarla en lugar de alquilarla.
Ejemplo 6.3 Determinación del punto de equivalencia. Caballa nacional vs importada para la industria de conservas de pescado
Analizar los costos de producción de conservas de pescado cuando se utiliza materia prima nacional o importada. Encontrar cuál es el precio (expresarlo en US$/cajón) de la materia prima nacional que resulta equivalente al precio pagado por la materia prima importada. El caso a estudiar corresponde a la situación argentina del año 1986, cuando aumentaron las importaciones de caballa H&G congelada, procedente del Ecuador, como alternativa para elaborar conservas. Paralelamente, cabe consignar que en Mar del Plata, existe una flota costera que, en forma estacional, se dedica a la captura de esta especie.
Datos comunes a ambas alternativas:
- Producción promedio bimestral: 1 000 000 latas de 380 g
- Envases, empaque, aceite y sal, se compran al comienzo de la temporada, pago contado.
- Pago de la mano de obra directa: quincenal.
- Pago de la mano de obra indirecta: mensual.
- Las ventas comienzan a partir del día 60.
- Tasa de interés promedio: 1% mensual
Caballa fresca (entera), nacional.
- Epoca de cosecha de la caballa en Argentina: 15 de noviembre - 15 de enero
- Pago de la materia prima a los 15 días de recibida (0,5 mes).
- Rendimiento promedio de la materia prima: 38%
Caballa D&E congelada, importada.
- Fecha de arribo del embarque: 15 de noviembre.
- Valor FOB: US$ 390/t
- Pago de la materia prima: a los 90 días
- Costo de importación (flete, seguro, etc): US$ 210/t (contado)
- Rendimiento promedio de la materia prima: 67%
Solución:
Se calculan el costo de producción equivalente (valor presente, con tiempo cero el 15 de noviembre) para cada una de las materias primas posibles, el que dependerá de factores como: rendimiento de la materia prima, valor del dólar de importación, valor de la tasa de interés mensual, etc. Se consideran aquellos factores que son distintos en cada alternativa, dado que existen ciertos insumos tales como: cantidad de latas, consumo del líquido de cobertura, ingreso por ventas, costos de mano de obra directa, costo de mano de obra indirecta, etc., que son iguales para una misma producción (en cantidad y tiempo de ocurrencia).
Se consideran dos alternativas de producción a partir de un modelo simplificado. Dichos esquemas de producción se limitan a un bimestre, pero en un análisis detallado se debería estudiar un programa de producción anual, conjuntamente con un pronóstico de ventas. Además, se deberían considerar los costos de oportunidad del capital de trabajo, es decir, incluir los costos financieros del uso de envases, materia prima, mano de obra y 30 días de producto terminado (Parin y Zugarramurdi, 1986b).
Para elaborar la producción requerida a partir de caballa nacional se estiman dos compras mensuales de materia prima. Para la caballa importada se efectúa una compra y se mantiene congelada, los costos de mantenimiento se abonarán cada 30 días, siendo su valor US$ 1/t × día.
Caballa nacional:
- Materia Prima
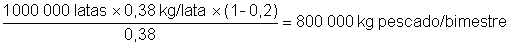
Son necesarios, entonces, 20 000 cajones/bimestre (1 cajón = 40 kg).
Costo Materia Prima (Ci): Se consideran precios entre US$ 10 y US$ 20/cajón.
CTi = 10 000 cajones × Ci × (1 + 0.01)-0,5 + 10 000 cajones × Ci × (1+0.01)-1,5
CTi = 10 000 cajones × Ci × [(1+0,01)-0,5 + (1+0.01)-1,5]
CTi = 10 000 cajones × Ci × (0,99504 + 0,98518)
CTi = 19 822,5 cajones × Ci.........(6.2)CT(1) = US$ 198 225,0 con C(1) = US$ 10/cajón
CT(2) = US$ 237 626,4 con C(2) = US$ 12/cajón
CT(3) = US$ 277 230,8 con C(3) = US$ 14/cajón
CT(4) = US$ 316 835,2 con C(4) = US$ 16/cajón
CT(5) = US$ 356 439,6 con C(5) = US$ 18/cajón
CT(6) = US$ 396 044,0 con C(6) = US$ 20/cajón
Caballa importada:
- Materia Prima
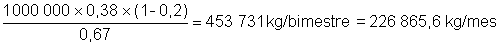
Costo FOB = US$ 390/t × 453,7 t = US$ 176 943
Costos de importación = US$ 210/t × 453,7 t = US$ 95 277
- Costos de almacenamiento en cámara:
Para su cálculo se estima un valor promedio del volumen de caballa a mantener durante el mes. Por día se procesan 7,5 t lo que implica en 30 días un consumo de 225 t. Si al inicio del primer roes el volumen en cámara era de 453,7 t, el valor promedio será de 339,35 t/día por lo que se abonarán:
El volumen promedio almacenado para el segundo mes de elaboración será de 117,4 t/día, al finalizar el mes habrá que pagar US$ 3 522. El valor presente equivalente de todos los gastos es (tasa promedio de interés 1% mensual, i = 0,01):
CT = 95 277 + 10 180,5 × (1+0,01)-1 + 3 522 × (1+0,01)-2 + 176 943 × (1+0,01)-3CT = US$ 280 531 (importada) .......... (6.3)
El punto de equivalencia está definido en este caso por la intersección de las Ecuaciones (6.2) y (6.3). Esto significa que se debe resolver la siguiente ecuación:
CT(x) = US$ 19 822,5 × C(x)CT = US$ 280 531
El punto de equivalencia será:
CT(x) = CT
de donde:
C(x) = 280 531/19822,5 = US$ 14,152/cajón
Este resultado indica que el punto de equivalencia se alcanza a un costo de US$ 14,15/cajón para el mercado interno. Los costos de la materia prima en el mercado interno por encima de este valor pueden inducir a las plantas conserveras nacionales a importar materia prima; por debajo de este valor, los industriales preferirán comprar la caballa de los pescadores locales. Puede ser útil encontrar el punto de equivalencia gráficamente (CT vs Ci, o CT por lata vs Ci) en particular si existe una variable adicional para estudiar, por ejemplo, la tasa real de interés (i). En la Figura 6.1, el caso discutido se resuelve gráficamente con un programa de producción anual y, se han agregado para su comparación, los casos para i = 0%, 2%, 3% y 4%.
En este ejemplo, es claro que mientras mayor es la tasa real de interés, menor es el precio (US$/cajón) al que los pescadores locales podrían vender su pescado para competir con la materia prima importada.
Ejemplo 6.4 Selección de equipos. Máquinas fileteadoras de pescado
Analizar las distintas alternativas tecnológicas para el procesamiento mecánico de filetes de merluza.
Solución:
Se calcularon los costos anuales equivalentes correspondientes a doce líneas mecánicas que resultaron de la combinación de los equipos utilizados en plantas industriales (descabezadoras, fileteadoras y cuereadoras) y los equipos de refrigeración, en Mar del Plata (Argentina). Las posibilidades incluyen equipos nacionales e importados. Del análisis de los resultados surge que existen dos conjuntos, aquéllos que disponen de una fileteadora tipo A de menor capacidad y que no realiza el corte V y otro conjunto con fileteadoras tipo B, de mayor capacidad y velocidad, que realiza el corte V.
Las diferencias observadas son las siguientes: rendimientos (mayor con fileteadora tipo A), consumo de mano de obra (mayor con la fileteadora tipo A) e inversión (mayor con fileteadora tipo B).
En la Tabla 6.3, se muestran los valores calculados para una capacidad diaria de 20 t de producto. Se supone que no hay variación en el rendimiento global de la operación. Los valores se expresaron en función del costo de la mano de obra, que es el factor de mayor cambio en los distintos países. Por ejemplo, en el costo de la hora-hombre en países en vías de desarrollo se observan valores que son 20 veces menores a aquéllos que perciben los operarios de países desarrollados.
Tabla 6.3 Inversión y costos de producción para líneas con fileteadoras tipo A y B
|
|
Máquinas Fileteadoras |
|
|
Tipo A |
Tipo B |
|
|
Inversión (US$) |
475 750 |
659 174 |
|
Costo de la Mano de Obra (US$/año) |
530 690 × CMO (US$/h) |
484 600 × CMO |
|
Costo de Mantenimiento (US$/año) |
238 680 |
208 680 |
|
Costos Fijos (US$/año) |
777 060 |
911 520 |
|
Vida útil (anos) |
10 |
10 |
El costo anual equivalente para la línea con fileteadora tipo A será:
AA = 475 750 × FPA + 530 690 × CMO + 238 680 + 777 060
siendo FPA(10%, 10 años) = 0,1627 (FPA, factor de recuperación de capital, Apéndice B Tabla B.2)
AA = 475 750 × 0,1627 + 530 690 × CMO + 238 680 + 777 060
AA = 1 093 144 + 530 690 × CMO
AB = 659 174 × FPA + 484 600 × CMO + 208 980 + 911 520
AB = 1 227 747 + 484 600 × CMO
El punto de equivalencia se determina igualando los costos anuales equivalentes:
AA = AB1 093 144 + 530 690 × CMO = 1 227 747 + 484 600 × CMO
CMO = US$ 2,92/h
Las funciones de costos y el punto de equivalencia se muestran en la Figura 6.2.
Para costos de hora-hombre superiores a US$ 2,92, la alternativa de utilizar la línea con fileteadora tipo B será la más económica. En caso contrario, será más conveniente la línea con fileteadora tipo A.
Este ejemplo muestra que la decisión de instalar una línea mecanizada de procesamiento de pescado puede ser una función del costo de mano de obra. La tendencia hacia máquinas más sofisticadas y automáticas para procesar camarón y pescado en el norte de Europa es un resultado de ello. Sin embargo, la necesidad de este tipo de estudios se manifiesta en países en desarrollo, por ejemplo, cuando se dispone de mano de obra insuficientemente calificada o cuando se debe alcanzar y mantener un dado nivel de calidad y seguridad.
Un rasgo importante del mundo industrial es el continuo perfeccionamiento de su trayectoria. La optimización es la presentación matemática de esta idea. Cualquier problema en el diseño, operación y análisis de plantas manufactureras y procesos industriales pueden ser reducidos en el análisis final al problema de la determinación del valor máximo o mínimo de una función de distintas variables.
Muchos métodos han sido introducidos para determinar procedimientos o políticas óptimas. Los métodos de optimización proporcionan medios eficaces y sistemáticos para seleccionar entre infinitas soluciones, como surgen de los problemas con un número grande de variables de decisión.
La técnicas de optimización pueden abarcar métodos analíticos y numéricos, que son seleccionados en función de la naturaleza de la función objetivo y las restricciones que conforman el modelo.
A fin de resolver los problemas más comunes en la industria pesquera, se citan dos técnicas de gran aplicación:
(a) Programación lineal (PL). Es una herramienta matemática que encuentra la solución óptima para el uso eficiente o asignación de recursos limitados, en sistemas lineales. Es la técnica más ampliamente usada para los análisis económicos.Los resultados obtenidos por PL también pueden ser alcanzados a partir de la determinación de la combinación óptima de recursos planteada en el tratamiento microeconómico de la producción. En este caso, los requerimientos de producción forman un conjunto de condiciones limitantes, similares a las que definen las isocuantas, y los precios de los insumos son representados por las líneas de isocostos.
Pueden mencionarse, asimismo, otras aplicaciones de la PL: problemas de control de inventarios, problemas de transporte, problemas de formulación de productos, etc.
(b) Programación dinámica (PD) Es una estrategia especialmente aplicable a la solución de problemas con múltiples etapas. Permite la descomposición de problemas complejos que no presentan reciclos en una secuencia de problemas de suboptimización más sencillos. Algunas aplicaciones de PD son: problemas de reemplazo, problemas de embarques, problemas de asignación de capital u otros insumos.
Por extensión, se han desarrollados técnicas numéricas para formular programas y efectuar control de proyectos. Estas técnicas son: Caminos crítico (CPM), y PERT (Program evaluation and review technique). Esta última se utiliza en el caso en que la estimación de tiempos, costos y resultados no pueden hacerse con exactitud, y deben emplearse conceptos de probabilidades y estadísticas para realizar las predicciones.
Ejemplo 6.5 Aplicación de programación dinámica. Operación de una planta integral procesadora de pescado (conservas, salado y congelado)
En este capítulo se presenta, como ejemplo de utilización de las técnicas de optimización, una comparación económica del funcionamiento de plantas integrales y de cada una de las plantas funcionando individualmente (Zugarramurdi y Lupín, 1976a). La planta integral está formada por plantas: de conservas, salado y congelado. Para simplificar el sistema en una primera etapa, se supone que la planta procesará, paralelamente, merluza (especie anual) y anchoíta, caballa o bonito (especies de cosecha).
Por la aplicación del principio de optimalidad de Bellman, se llega a una suboptimización secuencial de un proceso en etapas, que es la estrategia denominada Programación Dinámica. Dado que este problema es divisible en una serie de etapas identificables con cada una de las plantas, se considera conveniente la aplicación de esta técnica para la búsqueda de la solución óptima. El sistema a ser optimizado es el que se muestra en la Figura 6.3, donde:
CA = entrada de anchoíta, t/día;
CM = entrada de merluza, t/día;
AC = cantidad a procesar de anchoíta en la planta de conservas, t/día;
AS = cantidad a procesar de anchoíta en la planta de salado, t/día;
A' = entrada de anchoíta en las plantas de salado y congelado, t/día;
MF = cantidad a procesar de merluza en la planta de congelado, t/día;
GC = beneficio riesgoso de la planta de conservas, US$/año;
GFS = beneficio riesgoso de las plantas de congelado y salado, US$/año.
En este esquema se han considerado las plantas de congelado y salado juntas, con la restricción de que toda la materia prima que se reciba debe ser procesada. Actualmente, el esquema resulta simplificado pues no se ha considerado a la merluza como materia prima de las plantas de conservas, hecho que ha acontecido en los últimos años. La consideración de esta opción modificaría el sistema planteado, con la introducción de la variable CM al sistema en el bloque correspondiente a la planta de conservas y otra variable de diseño en dicho bloque, MC, cantidad a procesar de merluza en la planta de conservas (t/día).
Figura 6.3 Programación dinámica: Flujo de información
La definición de todo problema de optimización es: maximizar o minimizar (optimizar) la función objetivo actuando sobre las variables de decisión considerando todas las restricciones del sistema a optimizar. Por ello, se puede enunciar el problema así:
- Función objetivo: Es el funcionamiento óptimo de una planta integral de elaboración de productos congelados, salados y/o marinados, conservas y harina de pescado. Como es una planta existente, con capacidad de producción definida, el criterio a utilizar será la maximización de la función beneficio riesgoso. La expresión matemática para cada planta individual es:
Máx G = BN - i × Iw - (i + h) × IF
donde:
G = beneficio riesgoso
BN = beneficio neto
i = tasa de retorno
Iw = capital de trabajo
h = grado de riesgo
IF = inversión fija
- Variables de diseño: Cantidades de anchoíta y merluza a procesar en cada planta.
- Restricciones para cada etapa: Las cantidades de cada especie que cada planta puede procesar estarán determinadas por su máximo valor y en ningún caso podrán exceder la capacidad total de la citada planta (restricción 1). Se supone que la entrada total de materia prima es siempre menor que la cantidad total que la planta integral pueda procesar; en caso contrario, el excedente será destinado a la cámara de almacenamiento en frío de materia prima (restricción 2).
Expuesto así el problema, es evidente que existen infinitas posibilidades para la distribución de materia prima entre las distintas plantas. El empleo de la técnica de la Programación Dinámica nos permite conocer la combinación óptima de variables para cada valor de entrada de materia prima. El Principio de Optimalidad de Bellman indica que la última etapa (salado y congelado) debe ser optimizada respecto a la alimentación que recibe de las variables de estado A' y CM. Esto significa que el valor de AS y MS que logren maximizar la función objetivo parcial GFS para cualquier valor de CM y A' es óptimo.
Optimizada la etapa última, se debe seleccionar el valor de AC que maximice la función parcial de la etapa de conserva más el máximo de la función anterior.
El último paso de esta estrategia de cálculo es la recuperación de la información a fin de confeccionar un plan óptimo para el funcionamiento de la planta integral, en función de las entradas diarias de materia prima. Esto puede esquematizarse con la siguiente secuencia de cálculo:
Datos = CA y CM(a) Del gráfico o tabla obtenidos en la optimización de la etapa de conservas, se obtiene el valor óptimo: AC*
(b) A' = CA - AC*
(c) Del gráfico o tabla obtenidos en la optimización de la etapa de salado y congelado, con los valores de A' y CM, se obtienen los valores óptimos: AS* y MS*.
(d) De las relaciones de diseño de esta última etapa, se obtienen:
AF* = A' - AS*MF* = CM - MS*
En la Tabla 6.4 se observan los valores de las variables de diseño para una planta integral, y los correspondientes a las plantas individuales, ambas para el caso de operación a saturación de materia prima (CA = 184,5 t/día y CM = 34,5 t/día). Un punto a discutir es la inclusión de la planta de harina. Si se agrega a la planta integral (lo que es lógico) el costo de materia prima será prácticamente nulo, ya que utilizará los recortes, residuos y material rechazado por las otras plantas. En cuanto a la planta individual, si trabaja con recortes y residuos deberá comprados.
En el caso de no incluir la planta de harina, el beneficio para la planta integral es de un 35%, mientras que si es incluida el incremento ascendería al 57%. Cabe destacar, que eventualmente una planta integral puede operar en uno de sus rubros, en este caso congelados, con un beneficio menor que el de la planta equivalente operando aislada.
Esta situación se da, puesto que el punto óptimo de la suma de plantas, no es necesariamente igual a la suma de los óptimos de las plantas individuales, por ellos las cantidades a procesar en la planta integral no son las correspondientes a los óptimos individuales, sino los que resultan de aplicar el método de programación dinámica al sistema. Por otro lado, puede extenderse la aplicación de este método a determinar la forma en que variarán los costos para un mismo producto elaborado por una planta individual y una integral. El resultado es una disminución de costos unitarios. Por ejemplo, en el caso de elaborar una conserva, el costo unitario del producto en la planta integral será 20% menor que en la de conservas individual.
Tabla 6.4 Comparación de una planta integral con plantas individuales
|
Planta |
Plantas Individuales |
Planta Integral |
|
Conservas |
AC = 150 |
AC= 131,1 |
|
Salado |
AS = 4,32 |
AS = 4,40 |
|
MS = 4,68 |
MS = 4,60 |
|
|
Congelado |
AF= 31,78 |
AF= 49 |
|
MF = 28.22 |
MF = 30 |
A pesar de que las técnicas de optimización no son utilizadas, con algunas pocas excepciones, en países en vías de desarrollo, si son utilizadas en los países desarrollados por las medianas y grandes empresas pesqueras y de alimentos, y las compañías consultoras que proveen asesoramiento técnico a la industria pesquera.
Las técnicas de optimización requieren de un profundo conocimiento técnico y analítico del sistema a ser optimizado. En muchos casos, esto implica la posibilidad de desarrollar un modelo matemático incorporando las variables más relevantes. La aplicación de las técnicas de optimización es relativamente común hoy en día en la mayoría de las industrias pesqueras.
La simulación para el gerenciamiento de la producción que las industrias pesqueras escandinavas esperan introducir para 1995 es básicamente un programa de optimización. En algunas máquinas y equipos de procesamiento de pescado también se han incorporado técnicas de optimización, por ejemplo, en los robots que utilizan técnicas de imágenes para eliminar espinas y cortar filetes en porciones. La optimización está también implícitamente incorporada en el diseño de compresores en etapas en refrigeración y en evaporadores multi-etapas de plantas de harina de pescado, mejorando la eficiencia y reduciendo los costos.
Las técnicas de optimización también han sido usadas, por ejemplo, para calcular tiempos de esterilización (o pasteurización) en productos en conservas, maximizando la retención de nutrientes o características de textura, y para optimizar el diseño del empaque (por ejemplo, máxima resistencia vs. mínimo material de empaque). En países donde la información sobre la composición de nutrientes en las etiquetas es obligatoria, como en EE.UU., los procesos que optimizan los nutrientes son esenciales. En muchos casos, tales procedimientos son el resultado de aplicar la investigación a nivel de la empresa y por lo tanto no está disponible públicamente.
Las técnicas de optimización son también utilizadas en el diseño y producción de alimentos para peces en acuicultura a fin de obtener la máxima cantidad de nutrientes a costo mínimo con las materias primas disponibles. Las técnicas de optimización son una parte de las técnicas modernas de gerenciamiento. A pesar de que aún no constituyen una herramienta de uso cotidiano para el tecnólogo pesquero en países en desarrollo, deberán ser incorporadas como tales si se piensa en la auto-sustentabilidad. El paso siguiente al uso de la ingeniería económica, es la aplicación de las técnicas de optimización.