6. MARCACIÓN

6.1 Ejercicios

La marcación de los peces puede ser utilizada en el estudio del crecimiento, movimiento y migración. Esta sección, sin embargo, se ocupa solamente del uso de los datos de marcaciones para determinar las tasas de mortalidad de la población, y el tamaño de esta última. (El crecimiento es tratado en la sección 3.) La suposición más simple es que los peces marcados están sujetos a tasas de mortalidad natural y por pesca constantes, las cuales son las mismas que para el resto de la población sin marcar. Estas tasas pueden ser estimadas separadamente, debido a que, al contrario de lo que sucede con la población natural, el número inicial en la población marcada es conocido con precisión.

Esto es, si N₀ peces son marcados en un cierto momento, el número N_t que vive al final de un tiempo t viene dado por:

N_t = N₀e^-(F+M)t (6.1)

La tasa a que éstos son capturados es igual al coeficiente de mortalidad por pesca multiplicado por el número de los individuos vivos, y viene dada, por tanto, por

, etc.,

en donde n = número de peces marcados recapturados.

El número total de recapturados desde t = 0, es decir, desde el momento de la marcación hasta el momento T, se obtiene mediante una integración, es decir:

Si se agrupan las recapturas en intervalos de tiempo T, el número n_r recapturado en el r-ésimo intervalo, entre los instantes rT, (r + 1)T, es:

(6.2)

(Nota: El primer intervalo después de la marcación es r = 0).

Conociendo N₀, el número de individuos capturados en intervalos sucesivos puede ser usado para obtener estimaciones de F y de M. En particular:

(6.3)

de modo que si se señalan en una gráfica los valores de log n_r respecto a los de r, se obtiene una línea recta cuya pendiente es - (F + M) T. (Una ecuación alternativa que constituye una forma más conveniente de ella es la ecuación 6.9). Usando este valor de (F + M), F puede ser estimado a partir del número de individuos recapturados en cada intervalo aplicando la ecuación (6.2) o del punto de intersección con el eje de las y, que, según la ecuación (6.3) es

Igualmente, el número total de recapturas durante un período t es

De donde, sustituyendo F + M, se puede obtener una estimación directa de F. Cuando t es muy grande, esta expresión se reduce a .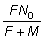

Por desgracia, no siempre se cumplen los supuestos de que se ha partido en este ejemplo simple. Los tipos de errores que pueden surgir pueden clasificarse en grupos definidos, según su efecto sobre las distintas estimaciones.

1. Errores que afectan al valor estimado de la tasa de pesca (F), pero no a la estimación de la mortalidad total (tipo A de RICKER, tipo 1 de BEVERTON y HOLT):

a) muerte de los peces inmediatamente después de ser marcados;

b) comunicación incompleta de las marcas recapturadas por los pescadores (a condición de que la proporción no comunicada se mantenga constante; una tasa variable de comunicación influiría también en la estimación de la mortalidad total).

2. Errores que influyen en la estimación de la mortalidad total, pero no en la de la mortalidad por pesca (tipo B, de RICKER, tipo 2, de BEVERTON y HOLT);

c) pérdida de las marcas, la cual ocurre a una tasa instantánea uniforme a lo largo de todo el experimento;

d) mortalidad adicional de los peces marcados que también se produce durante todo el experimento;

e) emigración de peces marcados.

3. Errores que influyen en la estimación tanto de la mortalidad por pesca como de la total;

f) la diferente vulnerabilidad a la pesca de los peces marcados y no marcados, por ejemplo, la posibilidad de que los peces marcados con discos de PETERSEN sean más fácilmente retenidos por la red;

g) los peces marcados no se mezclan uniformemente con el resto de la población sin marcar.

Los errores del tipo 1 nos llevarán a subestimar la verdadera mortalidad por pesca. Esta subestimación, a pesar de todo, puede ser útil en muchos casos. A menudo los errores pueden ser detectados y posiblemente medidos mediante observaciones oportunas. Así, en condiciones adecuadas, los peces marcados pueden ser conservados en tanques o cajas y se puede observar directamente su mortalidad en el período posterior a la marmación. En forma menos directa, se pueden comparar los porcentajes de peces recapturados que al ser marcados estaban en diferentes condiciones - muy activos o poco activos, dañados o aparentemente en buenas condiciones, etc., o fueron capturados por diferentes métodos. Si hay alguna mortalidad debida a la conmoción producida por la captura y la marcación, tal mortalidad será probablemente menor en los peces activos, y mayor en los peces magullados o dañados (la pérdida de escamas parece ser a menudo particularmente crítica). La no existencia de tal diferencia puede tomarse como indicación, aunque no como prueba, de que tal mortalidad es pequeña o no existe en absoluto.

La no comunicación de la recogida de marcas puede descubrirse a menudo comparando el número de marcas devueltas por cada unidad de cantidad de peces capturados por varios grupos de barcos que pescan en la zona donde se encuentran los peces marcados - barcos individuales, de diferentes países, etc. También se puede medir directamente introduciendo un número conocido de peces marcados en las capturas; esto es, la práctica usual con los métodos mecánicos de recuperación (por ejemplo, imanes en las fábricas de harina de pescado), pero puede ser usado, particularmente con la cooperación de algunos pescadores, para las marcas externas normales devueltas por los pescadores o por los trabajadores en tierra.

Las pérdidas del tipo 2 pueden considerarse como una causa adicional de «mortalidad», es decir, desaparición de individuos de la población de peces marcados, de modo que la ecuación (6.1) debe escribirse

(6.4)

en la que X incluye todas las causas de reducción del número de peces marcados que no sean debidas a la pesca - pérdidas de las marcas y emigración, a la vez que la mortalidad natural. La ecuación (6.4) y la forma correspondientes de la ecuación (6.2)

(6.5)

serán las usuales para el análisis de datos de marcaciones, de manera que, en realidad, solamente la mortalidad por pesca de la población natural será estimada por marcaciones. La mortalidad natural se obtendrá por sustracción de la mortalidad total Z, estimada de la composición por edades, etc.

Algunas veces pueden obtenerse estimaciones cuantitativas de las pérdidas del tipo 2, como, por ejemplo, las pérdidas de las marcas (pero no la mortalidad de los peces marcados), fijando dos marcas a cada pez y tomando nota de la proporción de peces recapturados con dos marcas, y con una sola marca, y del cambio de esta proporción con el tiempo.

La diferencia de vulnerabilidad a la pesca de los peces marcados puede eliminarse generalmente mediante el empleo de un tipo adecuado de marcas. Los peces que llevan marcas de botón es probable que sean particularmente vulnerables a ciertos artes de pesca - por ejemplo, las redes fijas - y, a ser posible, tales marcas no deberán ser usadas cuando se emplea este tipo de artes, pero si se tienen que usar, o si se quieren interpretar datos anteriores, el grado de mortalidad adicional por pesca puede medirse comparando las tasas de las recapturas de peces con diferentes tipos de marcas.

Una distribución de los peces marcados diferente de las de los no marcados constituirá probablemente uno de los problemas más difíciles. Si la mezcla es relativamente rápida, las recapturas durante un cierto período inicial, de 0 a t', durante el cual los peces marcados se están mezclando con la población sin marcar, pueden ser omitidas en los cálculos. El análisis se lleva a cabo entonces a partir del instante t' con un número inicial de marcas reducido, utilizando la ecuación (6.1) en la forma:

(6.6)

N₀' es estimado a partir del número de individuos marcados, restando el número recapturado en el período inicial de mezcla y el número estimado de pérdidas por otras causas, X. Esta última estimación habrá de proceder de un análisis de los datos posteriores. Sin embargo, en muchos casos la mayoría de las recapturas serán hechas antes de que las poblaciones marcadas y sin marcar se hayan mezclado ni siquiera aproximadamente.

Esta mezcla puede ser acelerada efectivamente mediante un sistema apropiado de marcación. El objeto es tener una relación entre peces marcados y sin marcar que sea la misma en toda la población. Esto podría obtenerse por ejemplo mediante una serie de arrastres espaciados uniformemente que cubran la totalidad del área, y marcando todos los peces capturados en cada estación, o una proporción constante de los mismos. Esto es posible en un área pequeña, pero no es fácil hacerlo digamos, por ejemplo, en el mar del Norte.

En una zona extensa tal como el mar del Norte puede no ser posible asegurar la mezcla efectiva de los peces marcados y sin marcar, o por lo menos puede ocurrir que en el momento en que se haya realizado la mezcla se haya obtenido ya la mayoría de las recapturas y, el no tener en cuenta el número de éstas lograda antes de que la mezcla fuera realmente completa significaría despreciar la mayor parte de los datos disponibles. Sin embargo, si se dispone de buena información sobre la distribución geográfica del esfuerzo pesquero, y sobre las posiciones en donse se han capturado las marcas devueltas, se pueden llevar a cabo estimaciones valiosas de la mortalidad por pesca en la población no marcada. Las operaciones lógicas son las siguientes:

a) Estimar la mortalidad por pesca F en la población marcada;

b) de la distribución del esfuerzo pesquero y de los peces marcados estimar la intensidad de pesca f sobre la población marcada;

c) seguidamente estimar q en la relación F = qf;

d) estimar la intensidad de pesca sobre la totalidad de la población;

e) a continuación, suponiendo que q tenga el mismo valor para los peces marcados y sin marcar, estimar la mortalidad por pesca en la totalidad de la población.

Deberá hacerse observar que, especialmente en las primeras de las citadas operaciones, no es necesario considerar la pesca por todos los barcos, o en todas las zonas, a condición de que, para calcular la mortalidad por pesca (valiéndose de las marcas devueltas) y la intensidad pesquera (a base de los datos sobre esfuerzo pesquero) se utilice la misma sección del total. Así, por ejemplo, en el mar de Norte algunos de los datos más detallados sobre esfuerzo pesquero corresponden a las actividades de pesca de los arrastreros de altura británicos; por consiguiente, puede ser conveniente calcular la mortalidad por pesca y la intensidad pesquera solamente a base de los datos de los arrastreros ingleses, y no hacer caso de las marcas devueltas y la actividad de pesca de los barcos ingleses dedicados a la pesca con redes de cerco y a la pesca costera, ni de la de los barcos de otros países.

Consideremos una pequeña área alrededor del lugar donde se lleva a cabo la marcación, en donde la mezcla de peces marcados y sin marcar tiene lugar rápidamente. Para un cierto intervalo de tiempo, i, sean

N_i = número de peces marcados presentes;
f_i = intensidad de pesca (esfuerzo por unidad de área y por unidad de tiempo);
n_i = número de peces marcados recapturados.

Tendremos

(6.7)

Si entonces se señalan en un gráfico los valores de 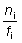(marcas recapturadas por unidad de intensidad de pesca) en relación con el tiempo, y se ajusta una curva a los puntos, la intersección de esta curva con el eje de las «y» será 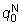, donde N₀ es el número de individuos liberados. De aquí puede estimarse q, y la mortalidad por pesca de la población en conjunto vendrá dada por

en que 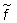es la intensidad de pesca efectiva sobre la población, calculada a partir de estadísticas detalladas de esfuerzo.

Aunque los siguientes supuestos puedan no estar completamente justificados podemos considerar, para una primera aproximación, que la intensidad de pesca en la pequeña área escogida alrededor del punto de liberación es constante y que el movimiento hacia el exterior de esta área puede definirse mediante un coeficiente exponencial constante, D, y por lo tanto, el número de peces marcados que quedan en el área después del tiempo t, N_t vendrá dado por

N_t = N₀e ^-(F+X+D)t

en la que F es la mortalidad por pesca existente en el área alrededor del punto de liberación, y no necesariamente la de la población en su totalidad. Si el i-ésimo intervalo es de duración T, y se extiende desde el momento 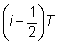hasta el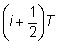

o

(6.8)

De esta forma, mientras (F + X + D)T sea pequeño, es decir, que el número no cambie mucho durante un intervalo de tiempo dado, el término entre paréntesis será aproximadamente igual a la unidad

(6.8')

y la representación gráfica de 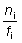en relación con el tiempo será una línea recta si se trata a escala logarítmica. Puede observarse que la ecuación (6.8), y particularmente su forma aproximada (6.8'), sugieren una buena alternativa para la ecuación (6.3) en la forma

(6.9)

en la que también se puede despreciar el último término si el cambio en número durante el intervalo de tiempo es pequeño, es decir, que si el logaritmo del número de individuos recapturados durante cada intervalo se señala gráficamente en relación con el punto medio del intervalo, entonces la traza obtenida deberá ser una línea recta, con pendiente - (F + M) T, y la intersección con el eje de las x será log FN₀T.

La ecuación (6.7) puede extenderse hasta abarcar datos de un área más vasta que el área pequeña que se ha supuesto alrededor del punto de liberación. Designando mediante prefijos los valores de las distintas áreas particulares

en donde 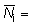total de peces marcados en las áreas analizadas,

número de peces marcados en el área j

y por consiguiente,

(6.10)

de forma que el análisis puede ser llevado a cabo como antes, utilizando la suma de las marcas devueltas por unidad de intensidad pesquera en cada pequeña zona. El análisis puede realizarse solamente cuando se disponga de un número suficiente de datos de esfuerzo. Si las marcas son recapturadas por una flota mixta, algunas de las cuales suministran datos adecuados de esfuerzo y otras no, entonces en todo el análisis se deberán utilizar solamente los datos de la flota o flotas que suministran datos completos tanto de esfuerzo como de marcas capturadas. Los peces marcados capturados por las otras flotas se consideran como pérdidas de otros tipos. Los datos de las demás flotas solamente se toman en consideración al final, al calcular la mortalidad por pesca en la población completa.

6.1 Ejercicios

1. GRAHAM (1938), marcó 1.000 bacalaos en el mar del Norte, y de ellos fueron recapturados los números siguientes, agrupados en intervalos de tres meses:

Meses	0-2	3-5	6-8	9-11
Número	139	91	52	40

Trazando el gráfico de los logaritmos de los números recapturados en función del tiempo, estímense los coeficientes de mortalidad total y por pesca. (Compárense los resultados obtenidos al usar la ecuación (6.3) y la forma aproximada de la ecuación (6.9)).

2. El merlán marcado y liberado en el mar de Irlanda fue clasificado según su vivacidad y el daño sufrido por sus escamas; el número liberado, y recapturado posteriormente, fue como sigue (datos de BEVERTON y BEDFORD, 1962):

Condición		Escamas	Número marcado	Número recapturado
	activo	buenas	60	18
	»	regulares	98	21
	»	malas	49	6
poco	activo	buenas	254	60
»	»	regulares	765	159
»	»	malas	509	43

¿Qué indicación hay de mortalidad de los peces al ser marcados? Asumiendo que todos los peces de mejor calidad sobrevivieron, ¿qué proporción de cada una de las otras categorías murió, y cuál fue el número efectivo liberado?

3. De un cierto número de bacalaos marcados en el golfo de San Lorenzo en 1955 las siguientes cantidades fueron devueltas por diferentes países en 1956 (según DICKIE, 1962):

País	Número de marcas	Desembarques totales de bacalao (toneladas)
Canadá	392	62,400
Francia	32	28,000
Portugal	29	5,800
España	15	8,100

Calcúlese el número de marcas devueltas por 1.000 toneladas de pescado desembarcado por cada país. ¿Qué prueba hay de que la devolución fuera incompleta? Si todas las marcas recapturadas por los pescadores canadienses fueron devueltas, estímese el número realmente recapturado por otros países.

4. En el verano de 1957 fueron liberados en el Mar del Norte tres grupos de arenques marcados con marcas internas. Existían disponibles datos detallados de la intensidad de pesca de los daneses en las áreas alrededor de los puntos de liberación, expresados en horas de pesca por cuadro estadístico (15 x 15 millas). El número de marcas recuperadas y la intensidad de pesca alrededor de cada punto donde se realizó la marcación, en las semanas siguientes a la marcación, fueron como sigue (datos adaptados del CIEM, 1961):

Semana después de la marcación	Grupo liberado
	1		2		3
	Marcas	Intensidad	Marcas	Intensidad	Marcas	Intensidad
1	21	80	80	420	3	10
2	35	64	12	60	3	5
3	30	53	10	50	8	15
4	8	26	2	10	2	10
5	10	56	1	10	-	-
Número marcado	3.000		1.500		3.000

Trácese el gráfico de las marcas recuperadas por hora pescando por cuadrado, para cada liberación. Partiendo de aquí, si la eficiencia de la técnica de recuperación es tal que el 90 % de las marcas capturadas son devueltas, ¿cuál es el valor de q, referido a una intensidad de 100 horas pescando, por cuadrado y semana?